Gabby says that 8 is a common multiple of 16 and 24. Mark says that 8 is a common factor of 16 and 24. Who is correct?
Answers
Answer:
gabby is correct
Step-by-step explanation:
Related Questions
Write an algebraic expression for the verbal description. The product of two consecutive odd integers, the first of which is 2n - 1
Answers
The algebraic expression for the given verbal description is (2n - 1)(2n + 1).
Let's break down the given verbal description step by step:
"Two consecutive odd integers": Let's represent the first odd integer as "x" and the second odd integer as "x + 2". Here, the second odd integer is obtained by adding 2 to the first odd integer."The first of which is 2n - 1": We are told that the first odd integer is equal to 2n - 1.Now, we can combine these two pieces of information into an algebraic expression: The product of the two consecutive odd integers can be represented as:
(x)(x + 2)
Since we know the first odd integer is 2n - 1, we can substitute it into the expression:
(2n - 1)(2n - 1 + 2)
Simplifying further:
(2n - 1)(2n + 1)
Therefore, the algebraic expression for the given verbal description is (2n - 1)(2n + 1).
To know more about integers check the below link:
https://brainly.com/question/17695139
#SPJ4
in a classroom at time t = 0, a sphere is thrown upward at a 45 angle to the horizontal at time while the sphere is still rising it bounces off the ceiling elastically
Answers
A sphere thrown upward at a 45-degree angle to the horizontal in a classroom elastically bounces off the ceiling while still rising
At time t = 0, a sphere is launched with an initial velocity at a 45-degree angle to the horizontal in a classroom. The sphere follows a parabolic trajectory as it rises due to the upward component of its initial velocity and experiences the downward pull of gravity. While the sphere is still ascending, it reaches the ceiling and collides with it.
During the elastic collision, the sphere's motion is reversed. It rebounds off the ceiling, changing its direction but maintaining its kinetic energy. As a result, the sphere starts descending with the same speed it had before the collision but in the opposite direction. The angle of descent will also be 45 degrees to the horizontal, mirroring the angle of the initial launch.
Throughout the entire process, neglecting air resistance, the total mechanical energy of the sphere is conserved since the collision with the ceiling is elastic.
learn more about initial velocity here:
https://brainly.com/question/31023940
#SPJ11
Your closet has 5 shirts for every 4 sweaters. Your closet has 15 shirts. How many sweaters are in your closet?
Answers
Answer:
12 sweaters
Step-by-step explanation:
Given data
We are told that there are 5 shirts for every 4 sweaters
If there are 15 shirts
We want to find the number of sweaters
for 5 shirts there are 4 sweaters
for 15 shirts there are x sweater
Cross multiply
15*4= 5*x
60= 5x
divide both sides by 5
x= 60/5
x=12 sweaters
Hence there are 12 sweaters
A graphing calculator is recommended. Find the maximum and minimum values of the function. (Round your answers to two decimal places.) y = sin x + sin 2x maximum value minimum value
Answers
The maximum value of the function is approximately 1.724 and the minimum value is approximately -1.724.
To find the maximum and minimum values of the function y = sin x + sin 2x, we can first take its derivative with respect to x:
y' = cos x + 2 cos 2x
Then, we can set y' equal to zero and solve for x:
cos x + 2 cos 2x = 0
We can use a graphing calculator to find the solutions to this equation, which are approximately x = 0.285 and x = 2.857. We can then evaluate the original function at these values to find the maximum and minimum values:
y(0.285) ≈ 1.724
y(2.857) ≈ -1.724
Therefore, the maximum value of the function is approximately 1.724 and the minimum value is approximately -1.724.
Learn more about value here:
https://brainly.com/question/13799105
#SPJ11
On which interval does h(t) have an average rate of change of zero?
Choose 1 answer:
(A
-10
B)
0
C)-5 < t < 0
D) 5
All the signs are equal or greater signs just so u know

Answers
Answer:
A
Step-by-step explanation:
Because the rate of change for a straight line is zero.
Try it by taking X and Y for Slope.
The base of a right prism is a right triangle. The lengths of the legs of the triangle are 3 meters and 5 meters. The volume of the prism is 30 cubic meters. Find the height of the prism
Answers
Answer:
15 meters
Step-by-step explanation:
jen smith has decided to become her own boss after spending 5 years as an assistant manager for a restaurant. the owner of a local sandwich store wants to sell the store to jen for $65,000 to be paid in installments of $13,000 in each of the next 5 years. according to the current owner, the store brings in revenue of about $110,000 per year and incurs operating costs of about 63% of sales. thus, once the store is paid for, jen should make about $35,000 -$40,000 per year before taxes. until the store is paid for, she will make substantially less-but she will be her own boss. realizing that some uncertainty is involved in this decision, jen wants to simulate what level of net income she can expect to earn during the next 5 years as she operates and pays for the store. in particular, she wants to see what could happen if sales are allowed to vary based on a normal distribution with mean of $100,000 and standard deviation of $10,000, and if operating costs are allowed to vary uniformly between 60% and 65% of sales. assume that jen's payments for the store are not deductible for tax purposes and that she is in the 28% tax bracket. a. create a spreadsheet model to simulate the annual net income jen will receive during each of the next five years if she decides to buy the store. (3 points) b. given the money she has in savings; jen thinks she can get by for the next five years if she can make at least $12,000 from the store each year. run 100 simulation (replication) and find the probability that jen will make at least $12,000 in each of the next five years? (1 point) c. what is the probability (based on 100 simulation) that jen will make at least $60,000 total over the next five years? (1 point)
Answers
Jen simulated her net income over 5 years assuming sales vary based on a normal distribution $100,000 and operating costs 60% and 65% of sales. keeping the loan payment be fixed at $13,000. The probability of making at least $12,000 each year is the number of successful simulations divided by 100. and at least $60,000 total over 5 years based as the number of successful simulations divided by 100.
To simulate Jen's annual net income over the next 5 years, a spreadsheet model can be created with columns for year, sales, operating costs, loan payment, and net income.
For each year, the sales can be generated from a normal distribution with mean $100,000 and standard deviation $10,000, and the operating costs can be generated from a uniform distribution between 60% and 65% of sales.
The loan payment can be fixed at $13,000, and the net income can be calculated as the difference between the sales, operating costs, loan payment, and taxes (28% of net income).
To find the probability that Jen will make at least $12,000 in each of the next five years, 100 simulations can be run using the model created in part a. For each simulation, the net income for each of the next five years can be calculated, and if the minimum net income is at least $12,000 for each year, then the simulation is counted as a success.
The probability of success can be calculated as the number of successful simulations divided by 100.
To find the probability that Jen will make at least $60,000 total over the next five years, 100 simulations can be run using the model created in part a. For each simulation, the total net income over the next five years can be calculated, and if it is at least $60,000, then the simulation is counted as a success.
The probability of success can be calculated as the number of successful simulations divided by 100.
To know more about Probability:
https://brainly.com/question/11234923
#SPJ4
You are given an expression for the volume of the rectangular prism. determine an expression for the missing dimension. v=4x^3 5x^2-32x-33 and the dimensions are (x 1)and (x 3)
Answers
4x^3 + 5x^2 - 32x - 33 / x + 1
4x^2 + x - 33
4x^2 + x - 33 / x + 3
4x - 11
Catelyn makes deposits of $1537 at the beginning of every 6
months into an account earning 2.07% compounded quarterly.
How much will she have after 3 years?
Answers
Catelyn will have approximately $1,647.62 in her account after 3 years of making deposits every 6 months.
To calculate how much Catelyn will have after 3 years, we need to determine the total number of compounding periods and then apply the compound interest formula.
Given:
Principal deposit (P) = $1537
Interest rate (r) = 2.07% per year (expressed as a decimal, r = 0.0207)
Compounding period (n) = 4 times per year (quarterly)
Time (t) = 3 years
First, we calculate the total number of compounding periods:
Number of compounding periods (N) = n * t = 4 * 3 = 12
Next, we can use the compound interest formula to calculate the future value (A):
A = P * (1 + r/n)^(n*t)
Plugging in the values:
A = $1537 * (1 + 0.0207/4)^(4*3)
A = $1537 * (1 + 0.005175)^12
A = $1537 * (1.005175)^12
A ≈ $1,647.62
Therefore, Catelyn will have approximately $1,647.62 in her account after 3 years of making deposits every 6 months.
Learn more about account here:brainly.com/question/24261944
#SPJ11
Find all the missing angles.
Please help
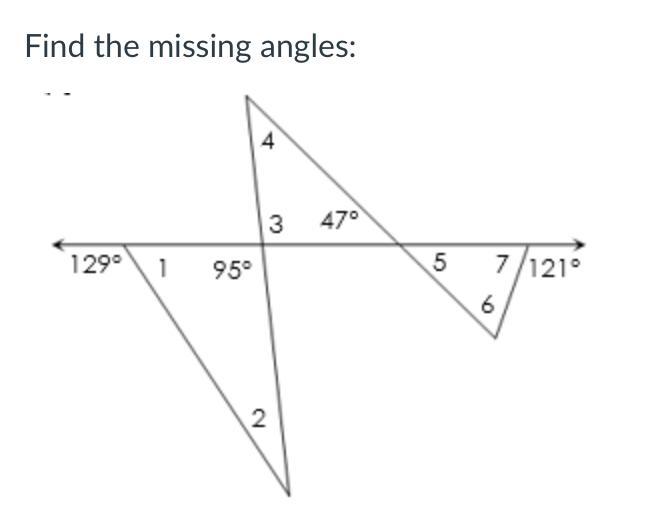
Answers
2: 34
3: 95
4: 38
5: 47
6: 74
7: 59
Hope this helps!
Brainliest and a like is much appreciated!
Comment if you want a explanation!
2. 34
3. 95
4. 38
5. 47
6. 74
7. 59
There is 46% hard working Elfs in the North Pole. there is 300 elfs in north pole. How many elfs are hard working
Answers
Answer:
138 hard working elfs
Step-by-step explanation:
the 46% of 300 is 138
Answer:
There is 138 Hard working Elves at the North Pole.
Step-by-step explanation:
300× 0.46= 138
Which change can be made to correct the chart
Answers
Answer:
what chart
Step-by-step explanation:
For a(3,8), b(-2,6) give the equation of the line perpendicular to line ab
Answers
The equation of the line perpendicular to line AB is determined as: y = (-5/2)x + 31/2.
How to Find the Equation of Perpendicular Lines?To find the equation of a line perpendicular to line AB, we need to determine the slope of line AB and then find the negative reciprocal of that slope.
Given points A(3,8) and B(-2,6), we can calculate the slope of line AB using the formula:
slope = (change in y) / (change in x)
slope = (6 - 8) / (-2 - 3) = -2 / -5 = 2/5
The negative reciprocal of 2/5 is -5/2.
Now we can use the point-slope form of a linear equation to find the equation of the line perpendicular to AB passing through point A (3,8):
y - y₁ = m(x - x₁)
Using the coordinates (x₁, y₁) = (3,8) and the slope m = -5/2, the equation becomes:
y - 8 = (-5/2)(x - 3)
y - 8 = (-5/2)x + (15/2)
Bringing 8 to the other side:
y = (-5/2)x + (15/2) + 8
y = (-5/2)x + 31/2
Learn more about Equation of Perpendicular Lines on:
https://brainly.com/question/7098341
#SPJ1
27^2x=3^x-7
SHOW WORK
Should get -7/5
Answers
The expression is simplified to x = -7/5
What are index forms?Index forms are simply described as mathematical forms that are used to represent numbers that are two large or small in more convenient forms.
They are also called the scientific notation or standard forms.
From the information given, we have that;
27^2x=3^x-7
Find the cube value of 27 and subsitute the value, we get;
3³⁽²ˣ⁾ = 3ˣ⁻⁷
cancel the common values, we get;
3(2x) = x - 7
expand the bracket
6x = x - 7
collect like terms
5x = -7
x = -7/5
Learn about index forms at: https://brainly.com/question/15361818
#SPJ1
two cards are drawn (without replacement) from an ordinary deck of 52 playing cards. what is the probability that these two cards is a pair?
Answers
Answer:
The probability that the two cards drawn form a pair is approximately 0.045.
Explanation:
There are 52 cards in an ordinary deck, and each card has a unique rank (ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, or king) and suit (spades, hearts, diamonds, or clubs). There are 13 ranks and 4 suits, so there are 13*4 = 52 possible cards in the deck.
When we draw two cards without replacement, there are 52 ways to draw the first card and 51 ways to draw the second card, for a total of 5251 = 2652 possible outcomes. Of these, there are 4 ways to draw a pair of cards with the same rank (for example, 2 of spades and 2 of hearts) and 13 ranks to choose from, so there are 413 = 52 pairs in the deck. Therefore, the probability of drawing a pair is 52/2652 = 1/51, or approximately 0.0196.
Alternatively, we can calculate the probability by considering the complement of the event (that is, the probability of not drawing a pair). There are 48 non-pair cards in the deck (since there are 52 total cards and 4 pairs), and there are 48*47 = 2256 ways to draw two non-pair cards. Therefore, the probability of not drawing a pair is 2256/2652 = 48/51, or approximately 0.931. The probability of drawing a pair is then 1 - 0.931 = 0.069, or approximately 0.045.
Either way, we can see that the probability of drawing a pair is relatively low, at about 4.5%.
Find ∬ R 2dA over the region R={(x,y)∣0≤x≤5,0≤y≤3} by identifying it as the volume of a solid
Answers
The given double integral is ∬ R 2dA over the region R = { (x,y) | 0 ≤ x ≤ 5, 0 ≤ y ≤ 3}. We can identify it as the volume of a solid. Therefore answer is 30.
We know that the integral of a function f(x,y) over a region R in the xy-plane is given by the double integral ∬ R f(x,y)dA. If we take the function f(x,y) to be constant, say f(x,y) = k, where k is a constant, then the double integral
∬ R f(x,y)dA gives us the area of the region R. If we take the function f(x,y) to be a variable, say f(x,y) = z,
where z is the height, then the double integral ∬ R f(x,y)dA gives us the volume of the solid that lies between the region R and the plane z = 0. So, we can identify the given double integral ∬ R 2dA as the volume of a solid that lies between the region R and the plane z = 0.
Let's find the limits of integration. We know that the limits of integration for x are from 0 to 5, and the limits of integration for y are from 0 to 3. Since the function f(x,y) = 2 is constant, we don't need to integrate it. So, the double integral is simply the product of the area of the region R and the height of the solid, which is 2. Therefore, the volume of the solid is
V = ∬ R 2dA
= 2 * Area of R
= 2 * (5 * 3)
= 30 cubic units.
Hence, the answer is 30.
For more information on integration visit:
brainly.com/question/31744185
#SPJ11
Determine whether the triangles are similar. If so, write a similarity statement.

Answers
Answer:
The triangles are not similar, because the corresponding angles are not congruent.
Step-by-step explanation:
what are the excluded values?

Answers
After divide, the solution of the expression is,
⇒ x (x + 2y) / 5
What is Division method?Division method is used to distributing a group of things into equal parts. Division is just opposite of multiplications. For example, dividing 20 by 2 means splitting 20 into 2 equal groups of 10.
Given that;
The expression is,
⇒ (x² - 4y²) ÷ (5x - 10y) / x
Now, We an simplify as;
⇒ (x² - 4y²) ÷ (5x - 10y) / x
⇒ (x² - (2y)²) ÷ (5x - 10y) / x
⇒ (x - 2y) (x + 2y) ÷ 5(x - 2y) / x
⇒ (x - 2y) (x + 2y) × x/ 5 (x - 2y)
⇒ x (x + 2y) / 5
Thus, The solution of the expression is,
⇒ x (x + 2y) / 5
Learn more about the divide visit:
https://brainly.com/question/28119824
#SPJ1
9. Choose the correct solution and graph for the inequality.

Answers
Answer:
x ≤ -9
Step-by-step explanation:
x-3 ≤ -12
x ≤ -12+3 (Isolate x)
x ≤ -9
38% adults favor the use of unmanned drones by police agencies. Twelve U.S. adults are randomly selected. Find the probability that the number of U.S. adults who favor the use of unmanned drones by police agencies is:
(a). exactly three: P(3) =
(b). at least four: P(x\geq4)=
(c). less than eight: P(x<8)=
Answers
The probability that the number of U.S. adults who favor the use of unmanned drones by police agencies is:
(a) P(3) = 0.2636
(b) P(x≥4) = 0.1814
(c) P(x<8) = 0.9997
(a) To find the probability that exactly three out of twelve U.S. adults favor the use of unmanned drones by police agencies, we can use the binomial probability formula:
P(3) = (12 choose 3) * (0.38)^3 * (1-0.38)^(12-3) = 0.2636
where (12 choose 3) = 12! / (3! * 9!) represents the number of ways to choose 3 out of 12 adults.
(b) To find the probability that at least four out of twelve U.S. adults favor the use of unmanned drones by police agencies, we can use the complement rule and subtract the probability of having three or fewer adults who favor the use of drones from 1:
P(x≥4) = 1 - P(x≤3) = 1 - [(12 choose 0) * (0.38)^0 * (1-0.38)^(12-0) + (12 choose 1) * (0.38)^1 * (1-0.38)^(12-1) + (12 choose 2) * (0.38)^2 * (1-0.38)^(12-2) + (12 choose 3) * (0.38)^3 * (1-0.38)^(12-3)] = 0.1814
(c) To find the probability that less than eight out of twelve U.S. adults favor the use of unmanned drones by police agencies, we can sum up the probabilities of having zero to seven adults who favor the use of drones:
P(x<8) = P(x=0) + P(x=1) + ... + P(x=7) = (12 choose 0) * (0.38)^0 * (1-0.38)^(12-0) + (12 choose 1) * (0.38)^1 * (1-0.38)^(12-1) + ... + (12 choose 7) * (0.38)^7 * (1-0.38)^(12-7) = 0.9997
Note that the probability of having eight or more adults who favor the use of drones is negligible.
For more questions like Probability click the link below:
https://brainly.com/question/30034780
#SPJ11
A. The point (3.5, 210) is on the graph. Explain what this means in terms of the car.
B. Is the point (1, 60) on this graph? Yes or no. Explain how you know

Answers
Answer/Step-by-step explanation:
A. The point (3.5, 210) on the graph means the car travelled a distance of 210 miles, at constant speed, for 3.5 hours.
B. To find out if the point (1, 60) is on the line, first, calculate the slope of the line (rate of change), and then find the rate of change between the point (1, 60) and the point (3.5, 210). If you get the same value as the slope of the line, it definitely means (1, 60) is a point of the graph.
Calculating slope of the line using (3.5, 210) and (5, 300):
\( slope(m) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{300 - 210}{5 - 3.5} \)
\( slope(m) = \frac{90}{1.5} \)
\( slope(m) = 60 \)
Calculating the rate of change (slope) between (1, 60) and (3.5, 210):
\( = \frac{y_2 - y_1}{x_2 - x_1} = \frac{210 - 60}{3.5 - 1} \)
\( = \frac{150}{2.5} = 60 \)
Rate of change (slope) = 60
Since the average rate of change between (1, 60) and the given point on the graph, (3.5, 210), is the same as the slope of the graph, therefore the point (1, 60) is a point on the graph also.
The answer is, YES.
What’s the answer in factor 5x + 5 =
Answers
dy/dt =y+2u, y(0)=5, u= step change of unity
Answers
The solution to the provided differential equation with the initial condition y(0) = 5 and u as a step change of unity is y = -2
The provided differential equation is: \(\[\frac{{dy}}{{dt}} = y + 2u\]\) with the initial condition: y(0) = 5 where u is a step change of unity.
To solve this differential equation, we can use the method of integrating factors.
First, let's rearrange the equation in the standard form:
\(\[\frac{{dy}}{{dt}} - y = 2u\]\)
Now, we can multiply both sides of the equation by the integrating factor, which is defined as the exponential of the integral of the coefficient of y with respect to t.
In this case, the coefficient of y is -1:
Integrating factor \(} = e^{\int -1 \, dt} = e^{-t}\)
Multiplying both sides of the equation by the integrating factor gives:
\(\[e^{-t}\frac{{dy}}{{dt}} - e^{-t}y = 2e^{-t}u\]\)
The left side of the equation can be rewritten using the product rule of differentiation:
\(\[\frac{{d}}{{dt}}(e^{-t}y) = 2e^{-t}u\]\)
Integrating both sides with respect to t gives:
\(\[e^{-t}y = 2\int e^{-t}u \, dt\]\)
Since u is a step change of unity, we can split the integral into two parts based on the step change:
\(\[e^{-t}y = 2\int_{{-\infty}}^{t} e^{-t} \, dt + 2\int_{t}^{{\infty}} 0 \, dt\]\)
Simplifying the integrals gives:
\(\[e^{-t}y = 2\int_{{-\infty}}^{t} e^{-t} \, dt + 0\]\)
\(\[e^{-t}y = 2\int_{{-\infty}}^{t} e^{-t} \, dt\]\)
Evaluating the integral on the right side gives:
\(\[e^{-t}y = 2[-e^{-t}]_{{-\infty}}^{t}\]\)
\(\[e^{-t}y = 2(-e^{-t} - (-e^{-\infty}))\]\)
Since \(\(e^{-\infty}\)\) approaches zero, the second term on the right side becomes zero:
\(\[e^{-t}y = 2(-e^{-t})\]\)
Dividing both sides by \(\(e^{-t}\)\) gives the solution: y = -2
To know more about differential equation refer here:
https://brainly.com/question/32524608#
#SPJ11
find the sum of the measures of interior angles of the indicated convex polygon
(a) nonagon (b)dodecagon c) 23-gon ?

Answers
(a) The sum of the interior angles of the nonagon is 1260°.
(b) The sum of the interior angles of the dodecagon is 1800°.
(c) The sum of the interior angles of the 23-gon is 3780°.
What is a convex polygon?
A convex polygon is a closed figure with all of its interior angles less than 180° and all of its vertices pointing outward. The term convex refers to a shape with a curve or a projecting surface. To put it another way, all of the lines across the outline are straight and point outwards.
The formula for the sum of the interior angle is (n -2)180°.
The number of sides of the nonagon is 9.
Putting n = 9 in (n -2)180°, to find the sum of interior angle of nonagon:
The sum of the interior angle is (9 -2)180° = 1260°.
The number of sides of dodecagon is 12.
Putting n = 12 in (n -2)180°, to find the sum of interior angle of dodecagon:
The sum of the interior angle is (12 -2)180° = 1800°
Putting n = 23 in (n -2)180°, to find the sum of interior angle of 23-gon:
The sum of the interior angle is (23 -2)180° = 3780°.
To learn more about the interior angle, click on the below link:
https://brainly.com/question/12228756
#SPJ1
Paul works Monday to Friday for a car recovery service in Mathcity. His records show that on any given day, the probability that he is called to recover a car in an area outside the city limits is 0.17. Calculate the probability that:

Answers
The probability that Paul has to recover a car is 0.1409 or 14.09%.
a) In one working week, there are 5 days.
We can use the binomial probability formula to calculate the probability of having more than three successes in 5 independent trials.
P(X > 3) = 1 - P(X ≤ 3)
Using the binomial probability formula:
P(X ≤ 3)
= C(5, 0) x (0.17)⁰ x (0.83)⁵ + C(5, 1) x (0.17)¹ x (0.83)⁴ + C(5, 2) x (0.17)² x (0.83)³ + C(5, 3) x (0.17)³ x (0.83)²
P(X <= 3) = 0.6244
Therefore, the probability that Paul has to recover a car outside the city limits more than three times in one working week is:
P(X > 3) = 1 - P(X ≤ 3) = 1 - 0.6244 = 0.3756
b) We can use the binomial probability formula again.
P(X > 3) = (P(X > 3))² = (0.3756)² = 0.1409
Therefore, the probability that Paul has to recover a car is 0.1409 or 14.09%.
Learn more about Binomial Distribution here:
https://brainly.com/question/29137961
#SPJ1
Help PLATOOOO PLEASE I NEED IT IM TRYING TO FINISH SUMMERTR SCHOOK

Answers
In order to prove that the product of the slopes of lines AC and BC is -1, the blanks should be completed with these;
"The slope of AC or GC is \(\frac{GF}{FC}\) by definition of slope. The slope of BC or CE is \(\frac{DE}{CD}\) by definition of slope."
"∠FCD = ∠FCG + ∠GCE + ∠ECD by angle addition postulate. ∠FCD = 180° by the definition of a straight angle, and ∠GCE = 90° by definition of perpendicular lines. So by substitution property of equality 180° = ∠FCG + 90° + ∠ECD. Therefore 90° - ∠FCG = ∠ECD, by subtraction property of equality. We also know that 180° = ∠FCG + 90° + ∠CGF by the triangle sum theorem and by the subtraction property of equality 90° - ∠FCG = ∠CGF, therefore ∠ECD = ∠CGF by the substitution property of equality. Then, ∠ECD ≈ ∠CGF by the definition of congruent angles. ∠GFC ≈ ∠CDE because all right angles are congruent. So by AA, ∆GFC ~ ∆CDE. Since the ratio of corresponding sides of similar triangles are proportional, then \(\frac{GF}{CD}=\frac{FC}{DE}\) or GF•DE = CD•FC by cross product. Finally, by the division property of equality \(\frac{GF}{FC}=\frac{CD}{DE}\). We can multiply both sides by the slope of line BC using the multiplication property of equality to get \(\frac{GF}{FC}\times -\frac{DE}{CD}=\frac{CD}{DE} \times -\frac{DE}{CD}\). Simplify so that \(\frac{GF}{FC}\times -\frac{DE}{CD}= -1\) . This shows that the product of the slopes of AC and BC is -1."
What is the slope of perpendicular lines?In Mathematics and Geometry, a condition that is true for two lines to be perpendicular is given by:
m₁ × m₂ = -1
1 × m₂ = -1
m₂ = -1
In this context, we can prove that the product of the slopes of perpendicular lines AC and BC is equal to -1 based on the following statements and reasons;
angle addition postulate.subtraction property of equality.the ratio of corresponding sides of similar triangles are proportional.multiplication property of equality.Read more on perpendicular line here: brainly.com/question/27257668
#SPJ1
X+3Y=6
Y=2X-5
What is the solution or if there’s infinitely solutions or no solution
Answers
Answer: slope
=
−
1
3
y-intercept
=
2
Explanation:
the equation of a line in
slope-intercept form
is.
∙
x
y
=
m
x
+
b
where m is the slope and b the y-intercept
rearrange
x
+
3
y
=
6
into this form
subtract x from both sides
x
−
x
+
3
y
=
6
−
x
⇒
3
y
=
−
x
+
6
divide all terms by 3
⇒
y
=
−
1
3
x
+
2
←
in slope-intercept form
⇒
slope
=
−
1
3
and y-intercept
=
2
graph{-1/3x+2 [-10, 10, -5, 5]}
Step-by-step explanation: Isolate the variable by dividing each side by factors that don't contain the variable.
X=Y /2+ 5/2
this would be y = (x+6)/3
then plug that y value into the other formula
(x+6)/3 = 2x - 15
then just solve for x
answer: x = 21
Use patterns to find the answer.
Thank you

Answers
Answer:
for 2 it's 2 4 6 8 10 12 14 16 18 20 22 24 and for three it's 3 6 9 12 15 18 21 24 27 30 33 36
Step-by-step explanation:
You Welcome
The times taken to assemble a clock at a factory are approximately normally distributed with a given mean y = 3 hr and
standard deviation o = 0.5 hr. What percentage of the times are between 2 hr and 4 hr?
34%
47.5%
68%
95%
Answers
The area between -2 and 2 is approximately 0.9545. Therefore, the percentage of times between 2 and 4 hours is 95%.
To find the percentage of times between 2 and 4 hours, we need to first standardize the values using the formula z = (x - mu) / sigma, where x is the value we are interested in (2 and 4), mu is the mean (3), and sigma is the standard deviation (0.5).
For 2 hours: z = \(\frac{(2 - 3)}{0.5}\) = -2
For 4 hours: z =\(\frac{(4 - 3)}{0.5}\) = 2
Next, we can use a standard normal distribution table or calculator to find the area under the curve between -2 and 2. This area represents the percentage of times between 2 and 4 hours.
According to the table, the area between -2 and 2 is approximately 0.9545. Therefore, the percentage of times between 2 and 4 hours is 95%.
So the answer is: 95%.
Learn more about percentage here:
https://brainly.com/question/16797504
#SPJ11
What is the solution to the equation: 2x-5 = -x+7
A: x=4
B: x=12
C: x=2
D: x=-4
Answers
Answer:
D: x=-4
Step-by-step explanation: