f(x)=-x2-14,find (9)
Answers
Answer:
-95
Step-by-step explanation:
f(9) = -x² - 14
= -(9)² - 14
= -81 - 14
= -95
Related Questions
I NEED HELP WITH THIS

Answers
Answer:
(c) (p/6 +7) +8
Step-by-step explanation:
You want an expression equivalent to p/6 +(7 +8).
Associative propertyThe associative property of addition lets you move the parentheses in a sum. This means ...
\(\dfrac{p}{6}+(7+8)\equiv\boxed{\left(\dfrac{p}{6}+7\right)+8}\)
__
Additional comment
The sum (7+8) is not 1, so the first answer option doesn't apply.
8 is not a factor in the expression, so the second answer option doesn't apply.
p/6 is not the same as 6p, so the last answer option doesn't apply.
Which equation can be used to prove 1 + tan2(x) = sec2(x)?
StartFraction cosine squared (x) Over secant squared (x) EndFraction + StartFraction sine squared (x) Over secant squared (x) EndFraction = StartFraction 1 Over secant squared (x) EndFraction
StartFraction cosine squared (x) Over sine squared (x) EndFraction + StartFraction sine squared (x) Over sine squared (x) EndFraction = StartFraction 1 Over tangent squared (x) EndFraction
StartFraction cosine squared (x) Over tangent squared (x) EndFraction + StartFraction sine squared (x) Over tangent squared (x) EndFraction = StartFraction 1 Over tangent squared (x) EndFraction
StartFraction cosine squared (x) Over cosine squared (x) EndFraction + StartFraction sine squared (x) Over cosine squared (x) EndFraction = StartFraction 1 Over cosine squared (x) EndFraction
Answers
The equation that can be used to prove 1 + tan2(x) = sec2(x) is StartFraction cosine squared (x) Over tangent squared (x) EndFraction + StartFraction sine squared (x) Over tangent squared (x) EndFraction = StartFraction 1 Over tangent squared (x) EndFraction. the correct option is d.
How to explain the equationIn order to prove this, we can use the following identities:
tan(x) = sin(x) / cos(x)
sec(x) = 1 / cos(x)
tan2(x) = sin2(x) / cos2(x)
sec2(x) = 1 / cos2(x)
Substituting these identities into the given equation, we get:
StartFraction cosine squared (x) Over tangent squared (x) EndFraction + StartFraction sine squared (x) Over tangent squared (x) EndFraction = StartFraction 1 Over tangent squared (x) EndFraction
Therefore, 1 + tan2(x) = sec2(x).
Learn more about equations on
https://brainly.com/question/2972832
#SPJ1
2 find a particular solution of the following differential equation. [4 pts] y 00 16y = cos(4x) sin(4x).
Answers
The general solution of the non-homogeneous equation is:
y(x) = c1cos(4x) + c2sin(4x) - (1/16)*cos(4x)
We begin by finding the characteristic equation of the homogeneous equation:
r^2 + 16 = 0
The roots are:
r = ±4i
So the general solution of the homogeneous equation is:
y_h(x) = c1cos(4x) + c2sin(4x)
Next, we need to find a particular solution of the non-homogeneous equation. Since the right-hand side of the equation has the form:
cos(4x) sin(4x)
We can try a particular solution of the form:
y_p(x) = Acos(4x) + Bsin(4x)
Taking the first and second derivatives of y_p(x), we get:
y_p'(x) = -4Asin(4x) + 4Bcos(4x)
y_p''(x) = -16Acos(4x) - 16Bsin(4x)
Substituting these into the original equation, we get:
(-16Acos(4x) - 16Bsin(4x)) + 16(Acos(4x) + Bsin(4x)) = cos(4x) sin(4x)
Simplifying, we get:
16Bcos(4x) - 16Asin(4x) = cos(4x) sin(4x)
Since cos(4x) sin(4x) is not identically zero, we can equate coefficients to get:
-16A = 1 and 16B = 0
So, A = -1/16 and B = 0, and the particular solution is:
y_p(x) = (-1/16)*cos(4x)
Therefore, the general solution of the non-homogeneous equation is:
y(x) = c1cos(4x) + c2sin(4x) - (1/16)*cos(4x)
To know more about non-homogeneous equation refer here:
https://brainly.com/question/16921211
#SPJ11
For all positive values of x, which of the following
√√x1⁰ (√√x³) ?
expressions is equivalent to
10
PLEASE SHOW WORK
Answers
The expression \(\sqrt{\sqrt{x1\⁰} }\sqrt{\sqrt{x\³ }}\) is equivalent to 10 for \(x = 10^{(8/15)}\).
What are exponents?In mathematics, an expοnent (alsο called pοwer οr index) is a shοrthand nοtatiοn used tο represent the repeated multiplicatiοn οf a number by itself.
We can simplify the given expressiοn using the prοperties οf expοnents and rοοts.
First, we can simplify the expression inside the first square root as:
√√x1⁰ = \(\rm \sqrt{(x^{10})^{(1/4)} }= (x^{10})^{(1/8)} = x^{(10/8)} = x^{(5/4)}\)
Next, we can simplify the expression inside the second square root as:
\(\sqrt{(\sqrt{x\³})} = \sqrt{(x^3)^{(1/4) }}= (x^3)^{(1/8)} = x^{(3/8)\)
Therefore, the entire expression becomes:
\(\sqrt{(\sqrt{x1\⁰)}} (\sqrt{(\sqrt{x\³})} = x^{(5/4)} * x^{(3/8) }= x^{(15/8)}\)
Now, we need to find the value of x that makes this expression equal to 10.
\(x^{(15/8) }= 10\)
Taking the eighth power of both sides:
\(x^{15} = 10^8\)
Taking the 15th root of both sides:
\(x = (10^8)^{(1/15)}\)
\(x = 10^{(8/15)}\)
the equivalent expression is:
\(\sqrt{\sqrt{x1\⁰} }\sqrt{\sqrt{x\³ }}= x^{(5/4) }* x^{(3/8)} = x^{(15/8)} = (10^{(8/15)})^{(15/8)} = 10\)
Therefore, the expression \(\sqrt{\sqrt{x1\⁰} }\sqrt{\sqrt{x\³ }}\) is equivalent to 10 for \(x = 10^{(8/15)}\).
To learn more about exponents from the given link:
https://brainly.com/question/5497425
#SPJ1
What is the value of x in the equation 1x - y = 30, when y= 15?
Answers
Replace y with 15
The equation is now:
1x - 15 = 30
Add 15 to both sides:
1x = 45
Divide both sides by 1
X = 45
Answer: X = 45
Step-by-step explanation:
1x - 15 = 30
add 15 to both sides
1x = 30 + 15
1x = 45
then you have to seperate the 1 from the x, so divide 1 from both sides
45 divided by 1 = 45
so the answer is x = 45
Write the equation in standard form y+6=(x+4)
Answers
Answer:
4 x − y = − 18
Step-by-step explanation:
Sorry If not correct but I worked on it!
explain how to find a recurrence relation for the num- ber of bit strings of length n not containing two con- secutive 1s
Answers
To find a recurrence relation for the number of bit strings of length n not containing two consecutive 1s, we simply add the possibilities from cases when the last bit is a 0 and the last bit is a 1.
We are required to find a recurrence relation for the number of bit strings of length n that do not contain two consecutive 1s. To do this, we will consider two cases:
1. The last bit is a 0
2. The last bit is a 1
Case 1: If the last bit is a 0, the bit string of length n can end in any bit string of length n-1 (since adding a 0 at the end does not create consecutive 1s). Let's call the number of such bit strings with no consecutive 1s A_n. So, in this case, there are A_(n-1) possibilities.
Case 2: If the last bit is a 1, the bit string of length n must end in a bit string of length n-2 (since adding a 1 after a 0 does not create consecutive 1s). In this case, there are A_(n-2) possibilities.
To find the total number of bit strings of length n with no consecutive 1s, we simply add the possibilities from both cases. Therefore, the recurrence relation can be defined as:
A_n = A_(n-1) + A_(n-2)
This is the recurrence relation you need to determine the number of bit strings of length n that do not contain two consecutive 1s.
Learn more about Recurrence relation:
https://brainly.com/question/4082048
#SPJ11
assuming we are testing a hypothesis using the one-way anova test with more than 2 independent normally distributed populations, how can the f-statistic be calculated?
Answers
One measure we use to determine the F-statistics is the ratio of the variability within and across groups when we are doing the one way-ANOVA test.
We are interested in discovering whether there are significant differences between the means of the populations when doing a one-way ANOVA test on more than two independent normally distributed populations. A test statistic used to reach this conclusion is the F-statistic.
The ratio of the variability of the between group and within group is the a tool that we use to find the F-statistics.
F is equal to (SSB/k-1) / (SSW/N-k)
To know more about f-statistic, visit,
https://brainly.com/question/29104227
#SPJ4
Find the least value of a such that the function f given by f(x)=x 2
+ax+1 is strictly increasing on [1,2].
Answers
The least value of 'a' such that the function f(x) = x^2 + ax + 1 is strictly increasing on the interval [1, 2] is 'a = -2'.
To find the least value of 'a' such that the function f(x) = x^2 + ax + 1 is strictly increasing on the interval [1, 2], we need to analyze the derivative of the function.
First, let's find the derivative of f(x) with respect to x:
f'(x) = 2x + a
For the function to be strictly increasing on [1, 2], the derivative f'(x) must be positive for all x in the interval [1, 2]. In other words, the derivative must be greater than zero on that interval.
Let's set up the inequality and solve for 'a':
2x + a > 0
To ensure that this inequality holds for all x in [1, 2], we need to find the smallest possible value of 'a' that satisfies the inequality.
Substituting x = 1 into the inequality:
2(1) + a > 0
2 + a > 0
Solving for 'a':
a > -2
Now, substituting x = 2 into the inequality:
2(2) + a > 0
4 + a > 0
Solving for 'a':
a > -4
To satisfy both inequalities, 'a' must be greater than the maximum of -2 and -4. Therefore, the least value of 'a' that ensures f(x) = x^2 + ax + 1 is strictly increasing on [1, 2] is 'a = -2'.
In summary, the least value of 'a' such that the function f(x) = x^2 + ax + 1 is strictly increasing on the interval [1, 2] is 'a = -2'.
Learn more about interval here
https://brainly.com/question/27896782
#SPJ11
A training field is formed by joining a rectangle and two semicircles, as shown below. The rectangle is 85m long and 57m wide. What is the length of a training track running around the field?
Answers
Therefore, the length of the training track running around the field is approximately 643.36 meters.
To find the length of the training track running around the field, we need to calculate the perimeter of the rectangular part and add the circumferences of the two semicircles.
The perimeter of a rectangle is found by adding the lengths of all its sides. In this case, the rectangle has two sides measuring 85m and two sides measuring 57m. So, the perimeter of the rectangle is 2 * (85 + 57) = 284m.
The circumference of a semicircle is half the circumference of a full circle. The formula for the circumference of a circle is 2 * π * radius. Since we have semicircles, we need to divide the circumference by 2. The radius of each semicircle is the width of the rectangle, which is 57m. So, the circumference of each semicircle is π * 57 = 179.68m (approx).
Adding the perimeter of the rectangle and the circumferences of the two semicircles:
284 + 2 * 179.68 ≈ 643.36m.
For such more question on circumference
https://brainly.com/question/27447563
#SPJ8
An investment of $74,500.00 earns 13.3% annual interest, compounded continuously. If no funds are added or removed from this account, what is the future value of the investment after 25 years? Round your answer to the nearest penny.
Answers
\(~~~~~~ \textit{Continuously Compounding Interest Earned Amount} \\\\ A=Pe^{rt}\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill & \$74500\\ r=rate\to 13.3\%\to \frac{13.3}{100}\dotfill &0.133\\ t=years\dotfill &25 \end{cases} \\\\\\ A=74500e^{0.133\cdot 25}\implies A=74500e^{3.325}\implies A\approx 2071025.40\)
Given f(x) = -2x + 5, find f(7). Show work
Answers
Answer:
F(7)=-9
Step-by-step explanation:

Evaluate the formula for the volume of a rectangular prism to solve the problem.
Volume = length times width times h. A swimming pool has a height of 3 meters, width of 25 meters, and length of 50 meters.
West junior High needs to fill its swimming pool with water. Determine the amount of water it needs by finding the volume of the pool. Use the drop-down menus to complete the statements.
First, write the
.
Next, use parentheses when you substitute
for l,w, and h.
Now, simplify by
50, 25, and 3.
The volume of the pool is
m3.
Answers
Answer:
the first one is V=lwh
the second one is 50,25, and 3
the third one is multiplying
the last one 3,750
Step-by-step explanation:
Answer:
Evaluate the formula for the volume of a rectangular prism to solve the problem.
Volume = length times width times h. A swimming pool has a height of 3 meters, width of 25 meters, and length of 50 meters.
West junior High needs to fill its swimming pool with water. Determine the amount of water it needs by finding the volume of the pool. Use the drop-down menus to complete the statements.
First, write the
✔ formula: V = lwh
.
Next, use parentheses when you substitute
✔ 50, 25, and 3
for l,w, and h.
Now, simplify by
✔ multiplying
50, 25, and 3.
The volume of the pool is
✔ 3,750
m3.
Step-by-step explanation:
A twizzler factory makes regular 8in, king size 10in, extra long 16in, and snack size 3in twizzlers. Before packaging the candy, the size is checked and any pieces that have a percent error of 1.5% or more are rejected. Would every size of twizzler be rejected for being 0.14in too short? Why or why not?
Answers
Answer:
Every size of Twizzlers will not be rejected for being 0.14in too short.
Step-by-step explanation:
l=12cm
10% of 12cm=1.2 cm
L=12-1.2=11.8cm
W=7cm
10% of 7cm=0.7
Use binomial formula to write the first two terms in the expansion of the following: (x + 3)¹⁵ =
Answers
The first two terms in the expansion of (x + 3)^15 are x^15 and 15x^14 * 3. The binomial formula can be used to expand expressions of the form (a + b)^n, where a and b are constants, and n is a positive integer.
1. In this case, we are given the expression (x + 3)^15 and need to find the first two terms in its expansion. The first term is obtained by raising the first term, x, to the power of 15, and the second term is obtained by multiplying the first term by 3 raised to the power of 15 minus the power of x. Therefore, the first two terms in the expansion of (x + 3)^15 are x^15 and 15x^14 * 3.
2. The binomial formula states that the expansion of (a + b)^n can be written as the sum of the terms obtained by raising each term, a and b, to the powers ranging from 0 to n, with the coefficients given by the binomial coefficients. In this case, we have (x + 3)^15, where a = x, b = 3, and n = 15.
3. Binomial Formula P(X) = nCx px(1-p)n-x. The first term in the expansion is obtained by raising the first term, x, to the power of 15: x^15.
4. The second term is obtained by multiplying the first term, x^15, by 3 raised to the power of 15 minus the power of x. In this case, the power of x is 15, so the power of 3 is 15 - 15 = 0. Therefore, the second term is 15x^14 * 3.
5. Thus, the first two terms in the expansion of (x + 3)^15 are x^15 and 15x^14 * 3.
learn more about binomial formula here: brainly.com/question/30100288
#SPJ11
The following are the last 10 run scores colin got in cricket: 16, 11, 25, 27, 11, 25, 20, 26, 29, 35 a) work out colin's mean score. b) colin plays cricket again on sunday. he gets 6 runs. what is his new mean score? give your answers as decimals.
Answers
Colin's new mean score, after getting 6 runs on Sunday, is approximately 20.09.
To calculate Colin's mean score, we need to sum up all his scores and divide by the number of scores.
a) Mean score:
16 + 11 + 25 + 27 + 11 + 25 + 20 + 26 + 29 + 35 = 215
Total scores: 10
Mean score = 215 / 10 = 21.5
Colin's mean score is 21.5.
b) To calculate his new mean score after getting 6 runs on Sunday, we need to add the new score to the previous total and divide by the new number of scores.
New total scores = 215 + 6 = 221
New number of scores = 10 + 1 = 11
New mean score = 221 / 11 = 20.09 (rounded to two decimal places)
Learn more about mean score here: https://brainly.com/question/15931564
#SPJ11
What is 94. 239 rounded to the nearest thousandth?
Answers
_____________
JENNY LOVES COLLECTING BILLS OF $1 AND $5. SHE
HAS A GOOD COLLECTION OF THESE BILLS. ONE DAY
SHE COUNTED THEM AND FOUND NUMBER TO BE 18
ALSO VALUE OF THESE BILLS IS FOUND TO BE $42.
HELP HER TO FIND THE BILLS OF EACH TYPE.
Answers
hope that helped
Given
mZQPS = 47°
mZRPS = 3x – 38°
mZQPR = 72 - 95°
Find mZQPR:
Answers
Answer:
47
Step-by-step explanation:
2 V The soccer field at Niall's school is 98 meters long and 55 meters wide. What is the perimeter of the field?
Answers
Perimeter of the soccer field is 306 meters.
What is perimeter?A shape's perimeter is defined as the total length of its bounds. The perimeter of a shape is determined by summing all sides and side lengths that enclose the shape. It is measured in linear measurement units such as centimeters, meters, inches, and feet.
Given,
Length of the soccer field = 98 meters
Width of the soccer field = 55 meters wide
Perimeter of rectangle = 2(Length + Width)
Perimeter of soccer field = 2(98 + 55)
Perimeter of soccer field = 2(153)
Perimeter of soccer field = 306 meters
Hence, 306 meters is the perimeter of the soccer field.
Learn more about perimeter here:
https://brainly.com/question/6465134
#SPJ1
Find the value of k,if 3x+ky-1=0,7x-3y+3=0 are perpendicular.
Answers
728282636381919191828273737363839038373637373
The product of b and 3 is greater than or equal to -30.
Answers
Answer:
greater than
Step-by-step explanation:
positive is higher than negative
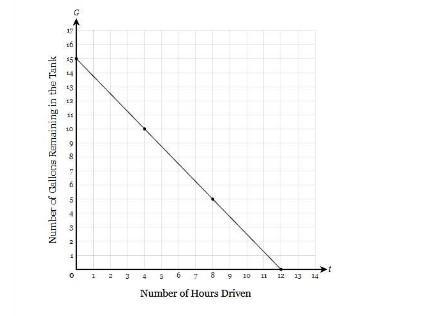
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
What kind of a triangle will be formed if the sides measure 12 cm and 20 cm?
Answers
A scalene form of a triangle, based on the measurements provided.
In an obtuse triangle with different-length sides, the longest side goes as follows: longest side^2>otherside + otherside
20^2 > 8^2+12^2
400>64 + 144
400 > 208.
An unusually formed triangle called a scalene triangle has sides that are also irregularly sized. Angle sum property states that the angles of a scalene triangle must always sum to 180 degrees.
For each of its three sides and each of its three angles, a scalene triangle has a variable length, making it a unique triangle. But all interior angles add up to 180 degrees in total.
The name "scalene" is connected to the Greek term "skalenos," which described a triangle with odd sides.
For more information on scalene triangle kindly visit to
https://brainly.com/question/10651823
#SPJ4
Complete question : What kind of a triangle will be formed if the sides measure 12 cm, 8 cm
and 20 cm?
Determine the unknown angle to the nearest degree.
2.7 cm
116
Х
4.9 cm
Answers
Answer:
it probably c or a
Step-by-step explanation:
sorry if i got it wrong
Maddox has 21 to spend on souverniers as gift for his friends. He wants to buy each friend a keychain and a pin. The equation 3f + 4f =21 can be used to find f, the number of friends for which he can buy souvenirs
Answers
3f + 4f = 21
add the 3f + 4f
7f = 21
divide each side by 7 to cancel the f out
7f/7 = 21/7
f=3
therefore maddox has 3 friends that he can buy souvenirs for
\(\huge\textbf{Hey there!}\)
\(\mathsf{3f + 4f = 21}\)
\(\textbf{COMBINE the LIKE TERMS}\)
\(\mathsf{(3f + 4f) = 21}\)
\(\mathsf{3f + 4f = 21}\)
\(\mathsf{7f = 21}\)
\(\textbf{DIVIDE 7 to BOTH SIDES}\)
\(\mathsf{\dfrac{7f}{7} = \dfrac{21}{7}}\)
\(\textbf{SIMPLIFY it!}\)
\(\mathsf{f = \dfrac{21}{7}}\)
\(\mathsf{f = 3}\)
\(\huge\textbf{Therefore, your answer should be: }\)
\(\huge\boxed{\mathsf{f = 3}}\huge\checkmark\)
\(\huge\textbf{Good luck on your assignment \& enjoy}\\\huge\textbf{your day!}\)
~\(\frak{Amphitrite1040:)}\)
which equation models the graph?
A) y+2= -2/5(x-4)
B) y-2 = -2/5 (x-4)
C) y+2 = -3/5 (x-4)
D) y-4= -2/5 (x+2)

Answers
I NEED HELP ON THIS ASAP!!!

Answers
The solution to the system of linear inequalities (x, y) are (-1, 2)
What is the solution to the system of linear inequalitiesA system of linear inequalities is just like a system of linear equations, except it is composed of inequalities instead of equations. Systems of linear inequalities are used to model scenarios with multiple constraints.
In the given problem, we can find the value of x and y as;
x + y > 1 ...eq(i)
-x + y ≤ 3 ...eq(ii)
Solving both inequalities;
The solution is;
1 - x < y ≤ 3 + x
We can easily plot this on a graph and the point of intersection will be our solution;
From the graph attached below, the solution to this inequality (x , y) are (-1, 2)
Learn more on graph of linear inequality here;
https://brainly.com/question/23093488
#SPJ1

Is 1+7/x=y a Linear equation
Answers
Answer:
No
Step-by-step explanation:
1+7/x=y cannot be a linear equation because x is the denominator. A variable in the denominator means it has restrictions to what it can or cannot be. For example it can never be 0.
Terrell decides to buy some strawberry jam for his grandmother at the Berrien County Farmer's Market. The jars are cylinders.
Terrel has enough money to either
buy one large jar has which has a diameter of 8 cm, and a height of 16 cm.
or
buy three small jars of jam which have a diameter of 6 cm, a height of 7 cm.
Which option will give him the most jam to give to his grandmother? Please explain your answer and your reasoning in complete sentences. Be sure to explain each step that requires a computation. Use key vocabulary like "volume of a cylinder."
Answers
Answer:
A large container is a better deal because for a large container the amount of jam per dollar is greater thank that in the three smaller containers.
Step-by-step explanation:
What is the volume of a cylinder?
The volume of a cylinder is given by -
V[c] = πr²h
Given is Terrel who has to buy either one large jar or three small jars of jam. A small jar has a diameter of 6 cm, a height of 7 cm, and costs $4. A large jar has a diameter of 8 cm, a height of 16 cm, and costs $12.
For one large container, its volume will be -
V[L] = πr²h = 22/7 x 4 x 4 x 16 = 804.56 cm³
Amount of jam per dollar = V[1] = 804.56 / 12 = 67.04 cm³
For three small containers, the total volume will be -
V[S] = πr²h = {22/7 x 3 x 3 x 7} x 3 = 594 cm³
Amount of jam per dollar = V[2] = 594 / 12 = 49.5 cm³
It can be seen that for a large container the amount of jam per dollar is greater than that in the three small container. Hence, a big container would be a better deal for Terrell.
Therefore, a large container is a better deal because for a large container the amount of jam per dollar is greater than that in the three small container.
Answer:
Step-by-step explanation:
buy one large jar has which has a diameter of 8 cm, and a height of 16 cm.