for a continuously differentiable function , that the hessian matrix be positive definite is what type of condition for a critical point of to be a local minimizer for ?
Answers
The given statement "Let f(x,y) be a c^2 function that has a local minimum point (0,0). Then the Hessian matrix of f at (0,0) is necessarily negative definite." is False. Because it ignores the possibility of the Hessian being indefinite.
If the Hessian matrix of a c^2 function f at a critical point (a,b) is positive definite, then f has a local minimum at (a,b). If the Hessian matrix is negative definite, then f has a local maximum at (a,b).
However, if the Hessian matrix is indefinite, then (a,b) is a saddle point of f, which is neither a local maximum nor a local minimum. Therefore, the statement "the Hessian matrix of f at (0,0) is necessarily negative definite" is false.
To know more about local minimum:
https://brainly.com/question/10878127
#SPJ4
--The given question is incomplete, the complete question is given
"Let f(x,y) be a c^2 function that has a local minimum point (0,0). Then the Hessian matrix of
f at (0,0) is necessarily negative definite. State if true or false."--
Related Questions
You spend £41.01 on groceries, £49.54 on fuel, and £12.50 on lottery tickets, how much do you have left from £105?
Answers
Answer:
£1.95
Step-by-step explanation:
£41.01 + £49.54 + £12.50 = £103.05
£105 - £103.05 = £1.95
Help me with this!!!

Answers
Answer:
it is second one
it is a RAY
True or False, you need to convert mixed numbers into improper fractions first when multiplying mixed numbers?
Answers
Answer : the answer is true
in a group of 10 college students, 4 are business majors. you choose 3 of the 10 students at random and ask their major. the distribution of the number of business majors you choose is:
Answers
The distribution of the number of business majors you choose is not binomial. The correct option is c) not binomial.
The distribution of the number of business majors you choose is not binomial because the conditions for a binomial distribution are not met:
1. There must be a fixed number of trials: In this case, we are choosing 3 students out of 10, which means the number of trials is not fixed.
2. The trials must be independent: This assumption is reasonable, as choosing one student does not affect the probability of choosing another student.
3. The probability of success must be the same for each trial: The probability of choosing a business major is 0.4 for the first trial, but it will change for the second and third trials depending on the results of the previous trials. Therefore, the probability of success is not the same for each trial.
Therefore, the correct option is c) not binomial.
The complete question is:
In a group of 10 college students, 4 are business majors. You choose 3 of the 10 students at random and ask their major. The distribution of the number of business majors you choose is
(a) Binomial with n = 10 and p = 0.4
(b) Binomial with n = 3 and p = 0.4
(c) Not binomial
For more about binomial:
https://brainly.com/question/30339327
#SPJ4
What is the domain of the function?
Domain: x

Answers
.1. Let A = {1,2,3}, B = {2,3,4}, and C = {3,4,5). Find An (BUC), (An B)UC, and (An B)U(ANC). Which of these sets are equal? 2. Provide examples of each of the following: (a) A partition of Z that consists of 2 sets (b) A partition of R that consists of infinitely many sets
Answers
The intervals start from 0 and increase by 1 for each subsequent set. The interval notation [a, b) represents all the real numbers greater than or equal to a and less than b.
1. Let's evaluate each set operation:
a) A ∩ (B ∪ C):
B ∪ C = {2, 3, 4, 5}
A ∩ (B ∪ C) = {2, 3} (the elements that are common to both A and (B ∪ C))
b) (A ∩ B) ∪ C:
A ∩ B = {2, 3}
(A ∩ B) ∪ C = {2, 3, 4, 5} (the elements that are either in A ∩ B or in C)
c) (A ∩ B) ∪ (A ∩ C):
A ∩ C = {3}
(A ∩ B) ∪ (A ∩ C) = {2, 3} (the elements that are either in A ∩ B or in A ∩ C)
Comparing the results:
A ∩ (B ∪ C) = {2, 3}
(A ∩ B) ∪ C = {2, 3, 4, 5}
(A ∩ B) ∪ (A ∩ C) = {2, 3}
From the above evaluations, we can see that (A ∩ B) ∪ C = (A ∩ B) ∪ (A ∩ C), so these two sets are equal.
2. Examples of partitions:
a) A partition of Z (integers) consisting of 2 sets:
{..., -2, 0, 2, 4, ...} and {..., -3, -1, 1, 3, ...}
b) A partition of R (real numbers) consisting of infinitely many sets:
{[0, 1)}, [1, 2), [2, 3), [3, 4), ...}
In this example, each set in the partition includes all the real numbers within a specific interval. The intervals start from 0 and increase by 1 for each subsequent set. The interval notation [a, b) represents all the real numbers greater than or equal to a and less than b.
Visit here to learn more about subsequent set:
brainly.com/question/31391639
#SPJ11
Consider the triangle with vertices (-7, -2), (-2, -5) , and (2, 3). What is the approximate perimeter of the triangle?
Answers
The perimeter of the triangle is 23.623 units.
What is perimeter of triangle?
Finding the distance around a triangle entails determining its perimeter. The distance formula can be used to calculate the side lengths if you don't already know all of them. The simplest way to find a triangle's perimeter is to add up all of its sides' lengths.
The distance between two points (x1,y1) and (x2,y2) can be determined using the following formula: √(x₂-x₁)² + (y₂ - y₁)²
Let the given vertices are (-7, -2), (-2, -5) , and (2, 3).
Distance formula for two points is = √(x₂-x₁)² + (y₂ - y₁)²
Using the formula,
AB = √((-2)-(-7))² +((-5)-(-2))²
= √(-2+7)² + (-5+2)²
= √5² + (-3)²
= √25 + 9
= √31
Similarly, BC = √(2 - (-2))² + (3-(-5))²
= √(2+2)² + (3+5)²
= √4² + 8²
= √16+64
= √80
CA = √((-7)-2)² + (-2 + 3)²
= √(-9²) + 1
= √81+1
=√82
Perimeter of triangle = AB + BC + CA
= √31 +√81 +√82
= 5.5677 + 9 + 9.0553
= 23.623
Therefore, the perimeter of the triangle is 23.623 units.
To know more about triangle check the below link:
https://brainly.com/question/17335144
#SPJ1
Deshaun is fertilizing his garden. The garden is in the shape of a rectangle. Its length is 14 feet and its width is 11 feet. Suppose each bag of fertilizer covers 22 square feet. How many bags will he need to cover the garden?
Answers
Answer:
length x width = area
14 x 11 = 154
154 / 22 = 7 fertilizer needed
Hope this helps
Step-by-step explanation:
\the graduate management admission test (gmat) is a standardized exam used by many colleges as part of the assessment for admission to graduate programs in business. the mean gmat score is 522 with a standard deviation of 111. the dataset used to compute these statistics is negatively skewed. what percentage of gmat scores are between 411 and 633?
Answers
Around 68.26% of GMAT scores fall within the range of 411 and 633.
To find the percentage of GMAT scores between 411 and 633, we can use the Z-score formula.
First, we calculate the Z-scores for both values:
Z1 = (411 - 522) / 111 = -1
Z2 = (633 - 522) / 111 = 1
Next, we use a Z-table or calculator to find the cumulative probability associated with each Z-score:
P(Z < -1) = 0.1587
P(Z < 1) = 0.8413
To find the percentage between the two scores, we subtract the lower cumulative probability from the higher cumulative probability:
P(-1 < Z < 1) = P(Z < 1) - P(Z < -1)
P(-1 < Z < 1) = 0.8413 - 0.1587 = 0.6826
Therefore, approximately 68.26% of GMAT scores are between 411 and 633.
In conclusion, around 68.26% of GMAT scores fall within the range of 411 and 633.
To know more about percentage visit:
brainly.com/question/32197511
#SPJ11
As the number of degrees of freedom for a t distribution increases, the difference between the t distribution and the standard normal distribution a. becomes larger. b. becomes smaller. c. stays the same. d. fluctuates.
Answers
As the number of degrees of freedom for a t-distribution increases, the difference between the t-distribution and the standard normal distribution (b) becomes smaller.
As the number of degrees of freedom for a t distribution increases, the difference between the t distribution and the standard normal distribution becomes smaller. This is because as the degrees of freedom increase, the t distribution approaches the normal distribution in shape and becomes more concentrated around the mean. Therefore, the t distribution becomes more similar to the standard normal distribution, which has a mean of 0 and a standard deviation of 1. So, the correct answer is b. becomes smaller.
Learn more about standard normal distribution here
https://brainly.com/question/26822684
#SPJ11
Help!! I need this ASAP!

Answers
The given expression rewritten in simplified exponential form is \(5x^{\frac{3}{2}}\)
Simplifying an expressionFrom the question, we are to rewrite the given expression is simplified exponential form.
The given expression is
\(\sqrt{\sqrt{25^{2} x^{6} } }\)
First, we will evaluate the inner square root
\(\sqrt{25^{\frac{2}{2} } x^{\frac{6}{2} } }\)
\(\sqrt{25 x^{3 } }\)
Simplifying further
\(\sqrt{25 } \times \sqrt{x^{3}}\)
\(5\times x^{\frac{3}{2}}\)
= \(5x^{\frac{3}{2}}\)
Hence, the expression in simplified form is \(5 x^{\frac{3}{2}}\)
Learn more on Simplifying an expression here: https://brainly.com/question/21862471
#SPJ1
what's the answer???
Answers
we have that
y=2x+1
the y-intercept (value of y when the value of x is equal to zero) is 1
so
is between the line y=2x+3 and the line y=2x-2
the line y=-2x+1 is not parallel to the other lines, because the slope is different
using a graphing tool
see the attached figure
please wait a minute

If g(x)=8x^6 and f(x) = log4 (2x) then f(g(x)) = ?
Answers
Answer:
f(g(x))= log4(2(8x^6))
or log4(16x^6)
Step-by-step explanation:
2O POINTS + BRAINLIEST || Which of these scale factors will result in an Enlargement?
A. 0
B. 1/2
C. 1
D.5
Answers
Answer:
D 5
Step-by-step explanation:
Answer:
B. 1/2?
Step-by-step explanation:
I need help like asap !!!
only numbers and decimal points

Answers
Answer:
b = 10.06 in
Step-by-step explanation:
Formula we use,
→ (AC)² = (BC)² + (AB)²
Now the value of a will be,
→ (10.5)² = b² + (3)²
→ 110.25 = b² + 9
→ b² = 110.25 - 9
→ b = √101.25
→ [ b = 10.06 in ]
Hence, value of b is 10.06 in.
A biker increased his average speed by 10 miles per hour in each successive 10-minute interval after the first interval. If in the first 10-minute interval, his average speed was 30 miles per hour, how many miles did he travel in the fourth 10-minute interval
Answers
The biker traveled 10 miles in the fourth 10-minute interval.
To solve this problem, we need to find the average speed for each interval and then calculate the distance traveled in the fourth interval.
Let's denote the average speed in the first interval as v1 (30 miles per hour) and the increase in speed for each successive interval as Δv (10 miles per hour). The average speed for each interval can be represented as follows:
Interval 1: v1 = 30 mph
Interval 2: v2 = v1 + Δv
Interval 3: v3 = v2 + Δv
Interval 4: v4 = v3 + Δv
We know that each interval is 10 minutes long, so the time (t) for each interval is also constant:
t = 10 minutes = 10/60 hours = 1/6 hours
Now, to calculate the distance traveled in each interval, we can use the formula:
Distance = Speed × Time
For the fourth interval, the distance traveled (D4) can be calculated as:
D4 = v4 × t
First, let's find the values for v2, v3, and v4:
v2 = v1 + Δv = 30 + 10 = 40 mph
v3 = v2 + Δv = 40 + 10 = 50 mph
v4 = v3 + Δv = 50 + 10 = 60 mph
Now we can calculate the distance traveled in the fourth interval:
D4 = v4 × t = 60 mph × 1/6 hours
D4 = 10 miles
Therefore, the biker traveled 10 miles in the fourth 10-minute interval.
Learn more about interval here:
brainly.com/question/24131141
#SPJ11
a bacon cheeseburger at a popular fast food restaurant contains 1564 milligrams (mg) of sodium, which is 68% of the recommended daily amount. What is the total recommended daily amount of
Answers
The recommended daily amount of sodium is approximately 2300 mg.
The total recommended daily amount of sodium for an average adult is around 2300 milligrams (mg). This value may vary depending on individual factors such as age, sex, and overall health conditions. The bacon cheeseburger at the popular fast food restaurant contains 1564 mg of sodium, which is approximately 68% of the recommended daily amount.
To calculate the total recommended daily amount of sodium, you would divide the sodium content of the bacon cheeseburger (1564 mg) by the percentage (68%):
1564 mg / 0.68 = 2294 mg
Therefore, the total recommended daily amount of sodium is approximately 2300 mg. It's important to note that this is a general guideline, and individuals with specific dietary needs or medical conditions may require a different sodium intake recommendation. It's always advisable to consult with a healthcare professional for personalized dietary guidance.
Learn more about average : brainly.com/question/30873037
#SPJ11
I NEED HELP PLEASE!! WILL GIVE CROWN!!
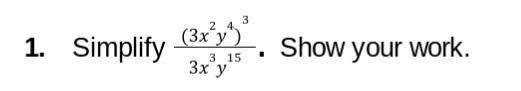
Answers
Answer:
9x^3/y^3
Step-by-step explanation:
Hope this helps!
It's dark. You have ten grey socks and ten blue socks you want to put into pairs. All socks are exactly the same except for their color. How many socks would you need to take with you to ensure you had at least a pair?
Answers
I think the answer is 4, you can't be sure with two
Answer:
3 socks
Step-by-step explanation:
Let's look at what outcomes you can have when you take one sock at a time for the first three picks.
First pick: grey
You have: 1 grey sock
Second pick: grey or blue
You have: 1 grey sock & 1 grey sock (a pair)
or 1 grey sock and 1 blue sock (no pair)
Third pick: grey or blue
You have: 2 grey + 1 grey (1 pair)
or 2 grey and 1 blue (1 pair)
or 1 grey sock, 1 blue sock, 1 grey (1 pair)
or 1 grey, 1 blue, 1 blue (1 pair)
Notice that obviously after the first pick, you cannot have a pair since you only took out one sock. After the second pick, you may or may not have a pair. After the third pick, you must have a pair.
Answer: 3 socks
Someone pls help me I’ll mark brainliest

Answers
Answer:
option 4
Step-by-step explanation:
it can't be greater or equal to so mark off the other ones and we also don't know how many games he played so put a variable beside that 2.5 hope this helps
Assume we have 3 boxes which contain red and black balls as follows, Box 1; 3 red balls and 7 black balls, Box 2; 6 red balls and 4 black balls, Box 3; 8 red balls and 2 black balls. suppose we draw a ball from box 1; if it is red, we draw a ball from box 2. if the ball drawn from box 1 is black, we draw a ball from box 3. a. what is the probability of red ball from box 1?. b. suppose we draw a ball from box 1 and it is red; what is the probability of another red ball when we draw from box 2 on the second round? c. suppose our first draw from box 1 was black; what is the conditional probability of our second draw from box 3 this time being red? d. Before we draw any ball; what is the probability of drawing two red balls at both draws? e. Before we draw any ball; what is the probability of drawing a red ball at first draw and a black ball at second draw?
Answers
a. The probability of drawing a red ball from Box 1 is 30%.
b. If a red ball is drawn from Box 1, the probability of drawing another red ball from Box 2 on the second round is 60%.
c. If the first draw from Box 1 was black, the conditional probability of drawing a red ball from Box 3 on the second draw is 80%.
d. The probability of drawing two red balls at both draws, without any prior information, is 46%.
e. The probability of drawing a red ball at the first draw and a black ball at the second draw, without any prior information, is 21%.
a. The probability of drawing a red ball from Box 1 can be calculated by dividing the number of red balls in Box 1 by the total number of balls in Box 1. Therefore, the probability is 3/(3+7) = 3/10 = 0.3 or 30%.
b. Since a red ball was drawn from Box 1, we only consider the balls in Box 2. The probability of drawing a red ball from Box 2 is 6/(6+4) = 6/10 = 0.6 or 60%. Therefore, the probability of drawing another red ball when the first ball drawn from Box 1 is red is 60%.
c. If the first draw from Box 1 was black, we only consider the balls in Box 3. The probability of drawing a red ball from Box 3 is 8/(8+2) = 8/10 = 0.8 or 80%. Therefore, the conditional probability of drawing a red ball from Box 3 when the first ball drawn from Box 1 was black is 80%.
d. Before any draws, the probability of drawing two red balls at both draws can be calculated by multiplying the probabilities of drawing a red ball from Box 1 and a red ball from Box 2. Therefore, the probability is 0.3 * 0.6 = 0.18 or 18%. However, since there are two possible scenarios (drawing red balls from Box 1 and Box 2, or drawing red balls from Box 2 and Box 1), we double the probability to obtain 36%. Adding the individual probabilities of each scenario gives a total probability of 36% + 10% = 46%.
e. Before any draws, the probability of drawing a red ball at the first draw and a black ball at the second draw can be calculated by multiplying the probability of drawing a red ball from Box 1 and the probability of drawing a black ball from Box 2 or Box 3. The probability of drawing a red ball from Box 1 is 0.3, and the probability of drawing a black ball from Box 2 or Box 3 is (7/10) + (2/10) = 0.9. Therefore, the probability is 0.3 * 0.9 = 0.27 or 27%. However, since there are two possible scenarios (drawing a red ball from Box 1 and a black ball from Box 2 or drawing a red ball from Box 1 and a black ball from Box 3), we double the probability to obtain 54%. Adding the individual probabilities of each scenario gives a total probability of 54% + 10% = 64%.
To learn more about probability click here: brainly.com/question/31828911
#SPJ11
1 point
11. A model of a planned baseball stadium is 2 ft wide. The actual stadium
will be 200 yd wide. What is the scale?
2 feet = 50 yards
1 foot = 100 yards
1 foot = 200 yards
1 foot = 50
Answers
2 x 100 = 200
Ally ran 5 miles in 36 minutes. If Ally runs at the same rate, how long would it take her to run 1 mile?
Answers
Answer:
7.2 Minutes
Step-by-step explanation:
Use Ratios
Miles : Minutes
5:36
Divide Both Sides By 5
1:7.2
It will Take Ally 7.2 Minutes To Run 1 Mile
HELP PLS THIS IS A TEST QUESTION
Which linear inequality is represented by the graph?
y<1/2x+2
y>1/2x+2
y<1/3x+2
y>1/3x+2

Answers
Answer:
y<1/2+2
Step-by-step explanation:
Answer:
I think the answer is A because I learned about slope last year
How many and what type of solutions does 5x2−2x+6 have?
1 rational solution
2 rational solutions
2 irrational solutions
2 nonreal solutions
Answers
Answer:
2 nonreal solutions
Step-by-step explanation:
given a quadratic equation in standard form
ax² + bx + c = 0 (a ≠ 0 )
then the nature of the roots are determined by the discriminant
b² - 4ac
• if b² - 4ac > 0 then 2 real and irrational solutions
• if b² - 4ac > 0 and a perfect square then 2 real and rational solutions
• if b² - 4ac = 0 then 2 real and equal solutions
• if b² - 4ac < 0 then no real solutions
5x² - 2x + 6 = 0 ← in standard form
with a = 5 , b = - 2 , c = 6
b² - 4ac
= (- 2)² - (4 × 5 × 6)
= 4 - 120
= - 116
since b² - 4ac < 0
then there are 2 nonreal solutions to the equation
what is (-4, 6); slope = -3
y= in slope intercept form
Answers
The slope intercept form is y=3x+18
Answer:
y = - 3x - 6
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
here m = - 3 , then
y = - 3x + c ← is the partial equation
to find c substitute (- 4, 6 ) into the partial equation
6 = 12 + c ⇒ c = 6 - 12 = - 6
y = - 3x - 6 ← equation of line in slope- intercept form
what is the probability that the number of calls among the 25 that involve a fax transmission exceeds the expected number by more than 2 standard deviations? (round your answer to three decimal places.)
Answers
0.003 is the probability that the number of calls among the 25 that involve a fax transmission exceeds the expected number by more than 2 standard deviations
To calculate the probability that the number of calls among the 25 that involve a fax transmission exceeds the expected number by more than 2 standard deviations.The mean is the expected number of calls involving a fax transmission, while the standard deviation is the measure of variability in the distribution. We then use this information to calculate the probability of exceeding the expected number by more than 2 standard deviations, which can be done using the z-score formula. The z-score for values more than 2 standard deviations away from the mean is 2.33, which corresponds to a probability of 0.003. Thus, the probability that the number of calls among the 25 that involve a fax transmission exceeds the expected number by more than 2 standard deviations is 0.003.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
PLA HELP ME THIS IS MY LAST CHANCE Use the given scale factor and the side lengths of the scale drawing to determine the side lengths of the real object

Answers
Answer:
Answer is C
Step-by-step explanation:
Because you divide each side by 2 because that is the scale factor
Find the measure of the arc or central angle indicated. Assume that lines which appear to be diameters are actual diameters

Answers
(11) The measure of angle IGJ is 46⁰.
(12) The measure of arc JH is determined as 138⁰.
What is the measure of the arc or central angle indicated?The measure of the arc or central angle indicated is calculated as follows;
(11) The measure of angle IGJ is calculated as follows;
m∠LGK = arc angle LK (interior angle of intersecting secants)
m∠LGK = 48⁰
m∠HGI = m∠LGK = 48⁰ (vertical opposite angles are equal)
m∠IGJ + m∠HGI + m∠JGK = 180⁰ (sum of angles in a straight line)
m∠IGJ + 48⁰ + 86⁰ = 180
m∠IGJ = 180 - 134
m∠IGJ = 46⁰
(12) The measure of arc JH is calculated as follows;
arc JH = arc JI + arc IH
arc JI = arc FG
arc FG = 180 - 137⁰ (sum of angle in a straight line)
arc FG = 43⁰
arc FG = arc JI (vertical opposite angles are equal)
arc JH = arc JI + arc IH
arc JH = 43⁰ + 95⁰
arc JH = 138⁰
Learn more about arc angles here: https://brainly.com/question/30543683
#SPJ1
La Michoacana bakery bakes 120 pieces
of sweet bread in 4 hours. At this rate,
how many pieces of sweet bread can be
baked in 12 hours?
PLS HURRY TELL ME
Answers
Answer:
120
Step-by-step explanation: