five and four hundred three thousandths in standard form
Answers
Answer:
5.403
Step-by-step explanation:
Five is 5. Four hundred three thousandths is .403. the 3 is in the thousandths the 4 is in the tenths and the 0 is in the hundredths, and the 5 is a whole number.
Related Questions
In a recent election, 63% of all registered voters participated in voting. In a survey of 275 retired voters, 162 participated in voting. Which is higher, the population proportion who participated or the sample proportion from this survey?
Answers
The population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
To determine whether the population proportion who participated in voting or the sample proportion from the survey is higher, we need to compare the percentages.
The population proportion who participated in voting is given as 63% of all registered voters.
This means that out of every 100 registered voters, 63 participated in voting.
In the survey of retired voters, 162 out of 275 participants voted. To calculate the sample proportion, we divide the number of retired voters who participated (162) by the total number of retired voters in the sample (275) and multiply by 100 to get a percentage.
Sample proportion = (162 / 275) \(\times\) 100 ≈ 58.91%, .
Comparing the population proportion (63%) with the sample proportion (58.91%), we can see that the population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
Therefore, based on the given data, the population proportion who participated in voting is higher than the sample proportion from this survey.
It's important to note that the sample proportion is an estimate based on the surveyed retired voters and may not perfectly represent the entire population of registered voters.
For similar question on population proportion.
https://brainly.com/question/29516589
#SPJ8
Find the slope of the line. 4x−4y=16 Enter your answer, in simplest form, in the box.
Answers
Answer:
y=x-4
Step-by-step explanation:
.When one increases the confidence level (1-α), say from 0.90 to 0.95,
Select one and explain:
a. margin of error will increase
b. the resulting confidence interval will capture the population parameter more often
c. both A and B are correct\
Answers
The correct answer is c. both A and B are correct. When one increases the confidence level from 0.90 to 0.95, the margin of error will increase because a higher level of confidence requires a wider interval to capture the population parameter.
However, the resulting confidence interval will also capture the population parameter more often because the higher confidence level provides a greater level of certainty that the interval contains the true population parameter.
When one increases the confidence level (1-α), say from 0.90 to 0.95, both A and B are correct.
Explanation:
a. The margin of error will increase because increasing the confidence level means we are more certain that the population parameter lies within the confidence interval. To achieve this, the interval has to be wider, which results in a larger margin of error.
b. The resulting confidence interval will capture the population parameter more often because a higher confidence level indicates a higher probability that the interval contains the true population parameter. In this case, going from a 0.90 to 0.95 confidence level means that we would expect the interval to capture the true population parameter 95% of the time, as opposed to 90% of the time.
Learn more about confidence level at: brainly.com/question/31748686
#SPJ11
Solving Differential Equation by Laplace Transform Solve the following initial value problems using Laplace transform and plase your solution using the indicated format 1. (D3+2D2+D+2)y=5+4sin(t):y(0)=3,y′(0)=1,y′′(0)=2 2. (D2+5D+6)y=5+3e3t:y(0)=5,y′(0)=0 3. (D2+6D+4)y=6ex+4t2:y(0)=4,y′(0)=2 Required: 1. Use laplace transforms 2. Find the laplace transform of the entire equation and set it implicitly (eqn1, eq 2 , eqn 3 ). 3. Plugin the initial conditions and save it as L_Eq1,L_Eq2, L_Eq3 4. Find the solution to the equation (ysoln1, ysoln 2 , ysoln3)
Answers
The value for given differential equation is ysoln1 = 3/10 + 1/2 cos t + 1/5 e-t (3 sin t + 2 cos t) + 1/5 e-t cos t, ysoln2 = 2 e-2t + 4 e3t + 2t e3t and ysoln3 = 2 t e t - 2 e t + e-2t.
The Laplace transform of the differential equation is :
D3 Y (s) + 2 D2 Y (s) + D Y (s) + 2 Y (s) = 5 + 4sin t
We know that,
L(Dn y(t))/dt^n = sn (L(y)) - sn-1 (y(0)) - sn-2 (y'(0)) - ... - sy(n-2) (0) - y(n-1) (0)
Putting n=0, 1, 2 in above formula, we get,
L(y) = Y (s), L(y') = sY (s) - y(0), L(y'')
= s2 Y (s) - s y(0) - y'(0)
= s2 Y (s) - 2s - 3
Substituting these values in the differential equation, we get :
s3 Y (s) - 3s2 - 3s + s Y (s) - 2 Y (s) = 5 + 4 L(sin t)
Taking Laplace transform of the differential equation, we get :
Y (s) = 5 s3 + s2 - 3s - 4s (s3 + 2s2 + s + 2
Using partial fraction, we get :
Y (s) = 1/2 s + 3/10 + 5/10 s + 7/10 s2 + 7/10 s + 1/5 (1/ (s2 + 2s + 1)) + (2 s - 1)/ (s2 + 2s + 1)
Taking inverse Laplace transform, we get :
ysoln1 = 3/10 + 1/2 cos t + 1/5 e-t (3 sin t + 2 cos t) + 1/5 e-t cos t
2. The Laplace transform of the differential equation is :
D2 Y (s) + 5 D Y (s) + 6 Y (s) = 5 + 3 e3t
We know that
L(Dn y(t))/dt^n = sn (L(y)) - sn-1 (y(0)) - sn-2 (y'(0)) - ... - sy(n-2) (0) - y(n-1) (0)
Putting n=0, 1 in above formula, we get,
L(y) = Y (s), L(y') = sY (s) - y(0)
Substituting these values in the differential equation, we get:s2 Y (s) - 5s - 6 + s Y (s) = 5 + 3 / (s - 3)
Taking Laplace transform of the differential equation,
we get :
Y (s) = 8 / (s - 3) + 1 / (s + 2) + 1 / ((s - 3)2)
Using partial fraction, we get :
Y (s) = 4 / (s - 3) + 2 / (s + 2) + 1 / (s - 3)2
Taking inverse Laplace transform, we get :
ysoln2 = 2 e-2t + 4 e3t + 2t e3t
3. The Laplace transform of the differential equation is :
D2 Y (s) + 6 D Y (s) + 4 Y (s) = 6 e x + 4t2
We know that
L(Dn y(t))/dt^n = sn (L(y)) - sn-1 (y(0)) - sn-2 (y'(0)) - ... - sy(n-2) (0) - y(n-1) (0)
Putting n=0, 1 in above formula, we get,
L(y) = Y (s), L(y') = sY (s) - y(0)
Substituting these values in the differential equation, we get :
s2 Y (s) - s y(0) - y'(0) + 6 s Y (s) - 6 y(0) + 4 Y (s) = 6 / (s - 1)2
Taking Laplace transform of the differential equation, we get :
Y (s) = 6 / (s - 1)2 (s2 + 6s + 4)
Using partial fraction, we get :
Y (s) = 2 / (s - 1)2 - 2 / (s - 1) + 1 / (s + 2)
Taking inverse Laplace transform, we get :
ysoln3 = 2 t e t - 2 e t + e-2t
Learn more about Laplace Transform from the given link :
https://brainly.com/question/29583725
#SPJ11
Explain why t distributions tend to be flatter and more spread out than the normal distribution.
Answers
t distributions tend to be flatter and more spread out than the normal distribution.
This is due to the fact that in the formula, the denominator is s rather than σ.
The distribution of the sample mean is normal if some samples are taken from a normal population with known variance. However, if the population variance is unknown, the distribution is not normal but Student-t with long tails. This means that sample means tend to be extreme when the population variance is unknown. Using the normal distribution instead of the t distribution to test the hypothesis increases the chance of error.
Note that there is a different t-distribution for each sample size. That is, the class of distributions. When talking about a particular t-distribution, we need to specify the degrees of freedom. The degrees of freedom for this t-statistic is given by the sample standard deviation s in the denominator of Equation 1. The spread is larger than the standard normal distribution. This is because the denominator of equation (1) is s, not σ. Because s is a random variable that changes from sample to sample, t becomes more volatile and more spread out.
Learn more about normal distribution here: https://brainly.com/question/27701525
#SPJ4
what is 3 3/4 - 2 1/5
Answers
Answer:
1 11/20
Step-by-step explanation:
3 3/4 - 2 1/5
(3-2) + (3/4 - 1/5)
1 + 11/20
1 11/20 or 31/20 or 1.55
At 9:30 A. M. Brittany tarted filling a 3,200 gallon pond at 11:30 A. M. He had filled 1,600 gallon. At what time will the pond be filled
Answers
The pond will be filled at 01:30 PM.
If Brittany started filling the pond at 9:30 A.M. and it takes him 1 hour to fill 1,600 gallons, then to fill 3,200 gallons, it will take him 3,200 / 1,600 = 2 hours.
The capacity of pond= 3600 gallon.
The Burt is started at 9:30 AM and filled 1600 gallons till 11:30 AM.
A unit of volume for measuring liquids. 1 gallon = 4 quarts = 8 pints = 16 cups = 128 fluid ounces. 1 US gallon = 231 cubic inches = 3.785411784 liters exactly.So, in 2 hours the Burt had filled 1600 gallons.
So, rate of filling = 1600/2=800 gallon/hour
The remaining volume of the pond = 3200-1600 = 1600 gallons
Time to fill the remaining volume = 1600/800=2 hour.
So, it will take 2 hours after 11:30 AM to fill the pond completely.
Hence, the pond will be filled at 01:30 PM.
For more such questions on capacity of pond
https://brainly.com/question/29725258
#SPJ4
For each problem; find the volume of the = solid that results when the region enclosed by the curves revolved about the given axis. 15) Vy -1, X=- Y= Axis: x = -1 A) ~[(5' = B) n[ (9: & 23 I =26.704 7 = 24.086 n[ (19: &y D) "[(52 ~C) 81 = 25.133 107 ~ 31.416'
Answers
The volume of the solid that results when the region enclosed by the curves is revolved about the axis x = -1 is approximately 26.704 units cubed.
To find the volume of the solid that results when the region enclosed by the curves is revolved about the given axis, we use the method of cylindrical shells. The formula for the volume of a cylindrical shell is:
V = 2πrhΔx
where r is the distance from the axis of rotation to the shell, h is the height of the shell, and Δx is the thickness of the shell.
In this case, the axis of rotation is x = -1. We need to find the limits of integration for x and y in order to set up the integral for each problem.
The curves are \(y = x^2 - 1, y = -x,\) and x = -1. Solving for x in terms of y for each curve, we get:
\(x =± \sqrt{(y+1} )\) for y in [-1, 1]
x = -y for y in [-1, 0]
The limits of integration for y are -1 to 0 for the segment of the curve y = -x, and -1 to 1 for the segment of the curve \(y = x^2 - 1\). The limits of integration for x are -1 to √(y+1) for the upper half of the parabola, and -√(y+1) to -1 for the lower half.
The integral for the volume is:
V = 2π ∫[-1,0] ∫[-1,0] (-x - (-1))y dx dy + 2π ∫[-1,1] ∫[-√(y+1),√(y+1)] (√(y+1) - (-√(y+1)))y dx dy
Simplifying and evaluating this integral, we get V = 26.704.
Therefore, the volume of the solid that results when the region enclosed by the curves is revolved about the axis x = -1 is approximately 26.704 units cubed.
For more such questions on volume visit:
https://brainly.com/question/463363
#SPJ11
2p.If k = am + 3mx, the value of m in terms of a, k,and x can be expressed asA.kat 3xk - 3mxB.C.k - am3xk-aD.3rYour answer
Answers
We are given the following
\(k=am+3mx\)we want to express m in terms of the other variables. So, what we will do is apply math operations on both sides, so we "isolate" the m variable on one side of the equation.
So, we begin by factoring the m on the right side, so we get
\(k=m\cdot(a+3x)\)Now, we divide both sides by (a+3x). So we get
\(m=\frac{k}{(a+3x)}\)which is our final answer.
Expand & simplify 3(y+5)-5(y-3)
Answers
Answer:
-2y + 30
Step-by-step explanation:
3(y+5)-5(y-3)
Distribute
3y+15 -5y +15
Combine like terms
-2y + 30
A mouse has made holes in opposite corners of a rectangular kitchen. Starting from its hole
in the northwest corner, the mouse scurries 20 feet along the length of the kitchen to reach a
piece of cheese in the southwest corner. Then the mouse scurries 15 feet along the width of
the kitchen to its other hole in the southeast corner. Finally the mouse scurries back to the
first hole. What is the total distance the mouse scurries?
Answers
Answer:
60 ft
Step-by-step explanation:
a² + b² = c²
20² + 15² = c²
c = √625
c = 25
total distance = 20 ft + 15 ft + 25 ft = 60 ft
Pls urgent help needed Bcz exam tmrw

Answers
The simplification of the expression 4a + 3b - a + 3b + 6 is 3(a + 2b + 2)
The expression im terms of x for the perimeter of the triangle is 31 = (3x - 5) + (2x - 1) + (x + 1)The value of x is 6How to find the perimeter of a triangle?Simplify 4a + 3b - a + 3b + 6
collect like terms
= 4a - a + 3b + 3b + 6
= 3a + 6b + 6
factorize
= 3(a + 2b + 2)
side a = 3x - 5
side b = 2x - 1
side c = x + 1
Perimeter = 31 cm
The perimeter of a triangle = side a + side b + side c
31 = (3x - 5) + (2x - 1) + (x + 1)
31 = 3x - 5 + 2x - 1 + x + 1
31 = 6x - 5
Add 5 to both sides
31 + 5 = 6x
36 = 6x
divide both sides by 6
x = 36/6
x = 6
Therefore, the value of x from the perimeter of the triangle is 6
Read more on perimeter of triangle:
https://brainly.com/question/24382052
#SPJ1
What is the volume of the composite solid? Use 3.14 for πr and round your answer to the nearest cm³.
A. 733 cm³
B. 707 cm³
C. 1099 cm³
D. 471 cm³
7 cm
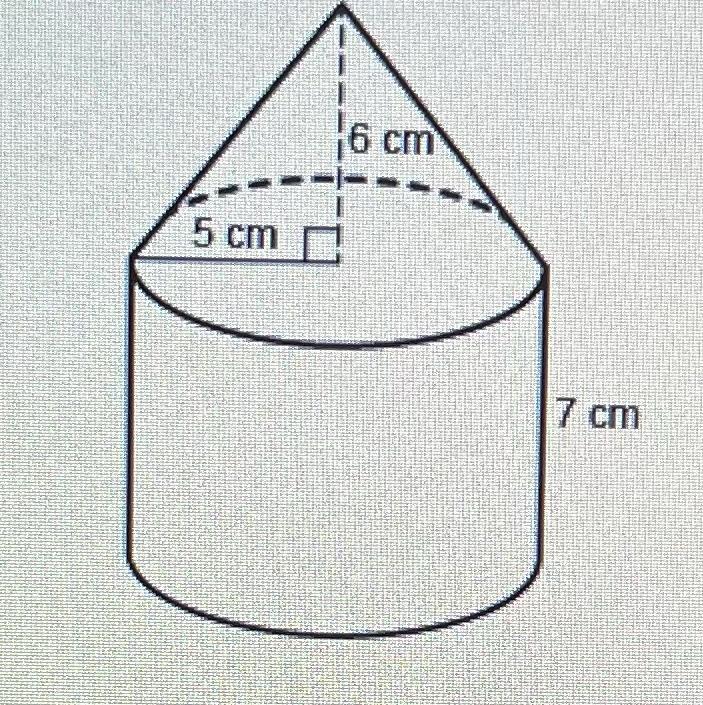
Answers
Answer:179 cm3
there you go :)
Step-by-step explanation:
Chloe earned a grade of 87% on her multiple choice math final that had a total of 200
problems. How many problems on the final exam did Chloe answer correctly?
Answers
200 x 0.87 = 174
She answered 174 questions correctly.
Answer:
Chloe answered 174 problems correctly.
Explanation:
To find percentage, you would multiply the percentages decimal to the total.
0.87x200=174
A scientist selected a random sample of seven varieties of peach ice cream to investigate the relationship between the density, in pounds per cubic inch, of the varieties of ice cream and the percent concentration of peaches in the ice cream. Assuming all conditions for inference are met, which of the following significance tests should be used to investigate whether there is convincing evidence at the 0.05 level of significance that a greater percent of peaches in the ice cream is associated with an increase in the density of the ice cream?
A. A two-sample t-test for a difference between means
B. A chi-square test of independence
C. A linear regression t-test for slope
D. A two-sample z-test for a difference between proportions
E. A matched pairs t-test for a mean difference
Answers
Answer:
The significance test that would be used to investigate whether there is convincing evidence at 0.05 level of significance that a greater percent of peaches in the ice cream is associated with an increase in the density of the ice cream is option C;
C. A linear regression t-test for slope
Step-by-step explanation:
The linear regression t-test for slope is a test for determining the existence of a statistically significant linear relationship between two variables, a independent variable, X and an dependent variable Y in the following form;
Y = B₀ + B₁·X
The test is used to test the regression line slope where we have;
B₀ = The constant
B₁ = The slope also known as the regression coefficient
The given information tested in the question is if an increase in the peaches in the ice cream is associated with an increase in the density of the ice cream, therefore, the test to investigate the relationship between the rate of both variables is the linear regression t-test for slope.
Therefore, we have
Y = B₀ + B₁·X
Where;
X = The percentage of peaches in the ice cream
Y = The density of the ice cream
estimate the error that is made by approximating the sum of the given series by the series the fitst 5 terms 1/k^3
Answers
The error involved in approximating the sum of the given series by the sum of the first five terms of the series is `R5 = 1/6³ + 1/7³ + ...`.
To estimate the error that is made by approximating the sum of the given series by the series the first 5 terms 1/k³, we can use the remainder term of a convergent series.
The given series is ∑ 1/k³ from k = 1 to infinity.We have to find the error involved in approximating the sum of the given series by the sum of the first five terms of the series.
That is, we need to find the difference between the actual sum of the series and the sum of the first five terms of the series.
The sum of the series is given by: `S = 1/1³ + 1/2³ + 1/3³ + 1/4³ + ... + 1/n³ + ...` We can use the remainder term of the series to find the error in approximation.
The remainder term `Rn` is given by: `Rn = Sn - S` where `Sn` is the sum of the first `n` terms of the series. Thus, we have to find the remainder term for `n = 5`.
The remainder term `Rn` is given by: `Rn = S - Sn = 1/6³ + 1/7³ + ...` Since the given series is convergent, the remainder term `Rn` tends to zero as `n` tends to infinity.
So, if we take the sum of the first five terms of the series, the error involved in approximation is given by the remainder term `R5`.
The error involved in this approximation is very small and can be neglected.
To learn more about : terms
https://brainly.com/question/30643700
#SPJ8
Lucía tiene un restaurante y encarga el siguiente pedido. 4523 kg de carne 3249 kg de pollo 20 kg de pescado 1814 kg de papa 2425 kg de arroz 3934 kg de granos y verduras ¿Cuánto pesa el pedido de Lucía?
A. 1781945 kg
B. 1781225 kg
C. 1802245 kg
D. 1802345 kg
Answers
Answer: 15965 kg
Step-by-step explanation:
\(4523+3249+20+1814+2425+3934=15965\)
surface area using a parametric description find the area of the following surfaces using a parametric description of the surface
The half-cylinder {(1, 0, z): r = 4,0 < 0 < 7,0 < z s 7}
Answers
The area of the half-cylinder can be found using a parametric description of the surface.
To find the area of the half-cylinder, we can parametrize the surface using cylindrical coordinates. Let's consider the surface as a function of two parameters, θ and z. We can define the parametric equations as follows:
x = r cos(θ)
y = r sin(θ)
z = z
In this case, the radius r is given as 4, the angle θ varies from 0 to 2π, and the height z varies from 0 to 7.
To calculate the surface area, we use the formula for the surface area of a surface described by parametric equations:
A = ∫∫ ||rθ × rz|| dθ dz
Here, ||rθ × rz|| represents the magnitude of the cross product of the partial derivatives of the parametric equations with respect to θ and z.
Learn more about parametric equations here:
https://brainly.com/question/29275326
#SPJ11
You are on a treasure-diving ship that is hunting for gold and silver coins. You reel in a wire basket that contains gold and silver coins, among other things. The basket holds no more than 50 pounds of material. Each gold coin weighs about 0.5 ounce, and each silver coin weighs about 0.25 ounce. You want to know the different numbers of each type of coin that could be in the basket. Explain why there cannot be 400 gold coins and 2800 silver coins in the basket.
Answers
Answer:
Cause it is more than 50 pounds
Step-by-step explanation:
Lily bought 11 3/4 metres of ribbon. Each metre costs $24.00. How much did Lily spend
Answers
Answer:
$282
Step-by-step explanation:
There is a bag with only red marbles and blue marbles.
The probability of randomly choosing a red marble is 7/10.
There are 42 red marbles in the bag and each is equally likely to be chosen.
Work out how many marbles in total there must be.
Answers
There is 60 total number of marbles in the bag for the probability of selecting a red marble is 7/10.
What is probabilityThe probability of an event occurring is the fraction of the number of required outcome divided by the total number of possible outcomes.
let the total possible outcome = x
probability of selecting a red marble = P(R) = 7/10
Given that there are 42 red marbles tgen:
42/x = 7/10
x = (42 × 10)/7 {cross multiplication}
x = 420/7
x = 60
Therefore, given the probability of selecting a red marble to be 7/10, the total number of marbles in the bag is derived to be 60
Read more about probability here:https://brainly.com/question/251701
#SPJ1
If tan(t)=4/9 what is tan(t−π)
Answers
The value of tan(t−π) is 4/9.
According to the statement
we have given that tan(t)=4/9 and we have to find the value of tan(t−π).
So,
tan(t−π) -(1)
take negative sign common from equation (1) it then
tan(t−π) = -tan(-t+π)
and we know that the according to the mathematics formula it become
tan(-t+π) is -tan t
then
tan(t−π) = -(-tan t)
it becomes
tan(t−π) = tan t
then its value becomes
tan(t−π) = tan(t)=4/9.
because we have given that the value of tan t is tan(t)=4/9.
So, The value of tan(t−π) is 4/9.
Learn more about the TRIGONOMETRY here https://brainly.com/question/24349828
#SPJ4
use Definition 1 to determine the Laplace transform of the given function. 1. t 2. t² 3. e⁶ᵗ 4. te³ᵗ 5. cos 2t
Answers
Using Definition 1 of the Laplace transform, we have determined the Laplace transforms of the given functions as mentioned above.
Definition 1 of the Laplace transform states that for a function f(t) defined for t ≥ 0, its Laplace transform F(s) is given by F(s) = L{f(t)} = ∫[0,∞] e^(-st) f(t) dt. Using this definition, we can determine the Laplace transforms of the given functions:
1. The Laplace transform of t is given by L{t} = 1/s².
2. The Laplace transform of t² is given by L{t²} = 2/s³.
3. The Laplace transform of e^(6t) is given by L{e^(6t)} = 1/(s - 6).
4. The Laplace transform of te^(3t) requires applying the property of the Laplace transform for the derivative of a function. The Laplace transform of te^(3t) is given by L{te^(3t)} = -d/ds (1/(s - 3)²).
5. The Laplace transform of cos(2t) requires using the trigonometric property of the Laplace transform. The Laplace transform of cos(2t) is given by L{cos(2t)} = s/(s² + 4).
In conclusion, using Definition 1 of the Laplace transform, we have determined the Laplace transforms of the given functions as mentioned above.
Learn more about Laplace transform here:
brainly.com/question/30402015
#SPJ11
8. The distribution of mass for United States pennies minted since 1982 is approximately normal with mean 2.5 grams. A random sample of 10 pennies minted since 1982 was selected. The sample had a mean mass of 2.47 grams and a standard deviation of 0.04 gram. The test statistic for the population mean has which of the following distributions? (A) A normal distribution with mean 0 and standard deviation 1 (B) A normal distribution with mean 2.5 and standard deviation 0.04 C A normal distribution with mean 2.47 and standard deviation 0.04 D At-distribution with 9 degrees of freedom E At-distribution with 10 degrees of freedom
Answers
If sample has mean-mass of 2.47 grams and standard-deviation of 0.04 gram, then test-statistic for population mean has (d) a "t-distribution" with 9 degrees-of-freedom.
A "test-statistic" is defined as a value calculated from a sample of data which is used in hypothesis testing.
The test statistic(t) for population mean can be calculated using formula:
⇒ t = (x' - μ)/(s/√n),
where x' = sample mean, μ = population mean, s = sample standard deviation, and n = sample size,
Substituting the values,
We get,
⇒ t = (2.47 - 2.5)/(0.04/√10) ≈ -2.38,
Since the population standard deviation is unknown, we need to use the t-distribution to find the p-value and make a conclusion about the null hypothesis.
The degrees-of-freedom for the t-distribution is = n - 1 = 10 - 1 = 9.
Therefore, the test statistic for the population mean has a t-distribution with 9 degrees of freedom, the correct option is (d).
Learn more about Degree Of Freedom here
https://brainly.com/question/30398137
#SPJ4
The given question is incomplete, the complete question is
The distribution of mass for United States pennies minted since 1982 is approximately normal with mean 2.5 grams. A random sample of 10 pennies minted since 1982 was selected. The sample had a mean mass of 2.47 grams and a standard deviation of 0.04 gram.
The test statistic for the population mean has which of the following distributions?
(a) A normal distribution with mean 0 and standard deviation 1,
(b) A normal distribution with mean 2.5 and standard deviation 0.04,
(c) A normal distribution with mean 2.47 and standard deviation 0.04,
(d) A t-distribution with 9 degrees of freedom,
(e) A t-distribution with 10 degrees of freedom.
If x is a continuous random variable then P(x≥A)=
A. P(X
B. 1-P(X>A)
C. P(X>A)
D. 1-P(X
Answers
If x is a continuous random variable then P(x≥A) = P(X>A). So, the correct option is C, i.e., P(X>A).
For a continuous random variable, the probability of X taking any specific value is zero, since there are infinitely many possible values that X could take. Instead, we calculate the probability that X falls within a certain range of values.
To find the probability that X is greater than or equal to A, we can use the cumulative distribution function (CDF) of X, denoted as F(X). The CDF F(X) gives the probability that X is less than or equal to a certain value x, i.e., F(X) = P(X ≤ x).
Now, since the event X ≥ A is the complement of the event X < A, we can use the complement rule to write:
P(X ≥ A) = 1 - P(X < A)
Using the definition of CDF, we get:
P(X ≥ A) = 1 - F(A)
Therefore, the probability of a continuous random variable X being greater than or equal to a certain value A is P(X>A) = 1 - F(A). This is the correct option C in the given question.
To learn more about continuous random variable click on,
https://brainly.com/question/23694159
#SPJ4
Complete question is:
If x is a continuous random variable then P(x≥A)=
A. P(X<A)
B. 1-P(X>A)
C. P(X>A)
D. 1-P(X≥A-1).
consider the matrix : what is the minimal approximation error achievable by a rank-1 approximation to ?
Answers
The minimal approximation error A-A 2achievable by a rank-1 approximation A to A is
||A - A1||₂=0 where A is 2×2 matrix.
We have given a matrix A as seen in above figure or A = [ 5 15 ; 6 18 ; -1 -3 ; -4 -12 ; 2 6]
note here that C₂= 3C₁
where Cᵢ --> iᵗʰ column
v = [ 5 ; 6 ; -1 ; -4 ; 2]
||v||² = 82 => ||v|| = √82
and A At v = 820 v
and A At = [ 82 246 ; 246 738]
AAt [1;3] = 820[1;3]
=> v1 = 1/√10(1,3)^t
Then the best rank of 1 approx
= √820 /√80√10 [ 5 ; 6 ; -1 ; -4 ; 2] [ 1 3]
= A
Since , the rank of matrix A is one so, the minimal approx. value is ||A - A1||2 = 0
Hence, the minimal Approx. ||A - A1||2 = 0 .
To learn more about minimal of matrix, refer:
https://brainly.com/question/19084291
#SPJ4
Complete question:
Consider the matrix A: A = [5 15] 6 18 -1 -3 -4 -12 [26] What is the minimal approximation error A-A 2 achievable by a rank-1 approximation A to A? Hint: Can you determine this without explicitly calculating the SVD?

Solve the proportion:
5
6
=
2
n
+
9
9
Answers
Step-by-step explanation:
\(56 = 2n + 99\)
Collect like terms and simplify
\(56 - 99 = 2n \\ - 43 = 2n\)
Divide both sides of the equation by 2
\( \frac{ - 43}{2} = \frac{2n}{2} \)
Simplify
\(n = - \frac{43}{2} = - 21 \frac{1}{2} \)
Solve for x on the diagram below

Answers
The value of x in the diagram is 100 degrees
How to determine the value of xFrom the question, we have the following parameters that can be used in our computation:
The figure
On the figure, we can see that:
The angle x and 100 degrees are alternate angles
Alternate angles have equal values
So, we have
x = 100
Hence, the value is 100 degree
Read more about angle at
https://brainly.com/question/25716982
#SPJ1
In the given figure, mBJ = 106 and FHJH. Which statement is true?
F
H
G
Figure not drawn to scale
K
106°
OA.
The measure of ZG is 21", and triangle FGH is isosceles.
OB.
The measure of ZG is 56", and triangle FGH is isosceles.
O.C.
The measure of ZG is 21", and triangle FGH is not isosceles.
The measure of ZG is 56", and triangle FGH is not isosceles.
D.

Answers
The 106° measure of arc \(m\widehat{HJ}\) and the length of the chords \(\widehat{FH}\) and \(\widehat{JH}\), which are the same, indicates that m∠G = 21° and ΔFGH is not isosceles. The correct option is option C;
C. The measure of ∠G is 21°, and triangle FGH is not isosceles
What is an isosceles triangle?An isosceles triangle is a triangle that have two sides of the same length and two angles of the same measure.
According to the outside angle to a circle theorem, the measure of the outside angle ∠G formed by the secant GJ and the tangent GF is equal to the difference of the measures of the arcs \(m\widehat{F'KJ}\), and arc \(m\widehat{FH}\) divided by 2.
\(m\widehat{F'KJ}\) = 360° - \(m\widehat{FH}\) - \(m\widehat{HJ}\)
\(\widehat{FH}\) = \(\widehat{JH}\)
\(\widehat{FH}\) ≅ \(\widehat{JH}\)
The lengths of the chord intercepted by congruent arcs are congruent.
Therefore; \(\widehat{JH}\) ≅ \(\widehat{FH}\)
Which indicates;
\(m\widehat{JH}\) = 106° = \(m\widehat{FH}\)
\(m\widehat{F'KJ}\) = 360° - 106° - 106° = 148°
m∠G = (\(m\widehat{F'KJ}\) - \(m\widehat{FH}\)) ÷ 2
m∠G = (148° - 106°) ÷ 2 = 21°
m∠G = 21°\(m\widehat{F'KJ}\) = 148°
m∠FHJ = 148° ÷ 2 = 74° (Angle at the center is twice angle formed at the circumference)
∠FHJ = ∠HFG + ∠G (exterior angle to triangle ΔFGH)
∠HFG = ∠FHJ - ∠G
Therefore; m∠HFG = 74° - 21° = 53°
m∠HFG = 53°
m∠FHG = 180° - 74° = 106° (linear pair angles property)
m∠G ≠ m∠FHG ≠ m∠HFG, therefore, ΔFGH is not isoscelesThe correct option is option C.
Learn more about the outside angle of a circle theorem here:
https://brainly.com/question/22227781
#SPJ1
What is the answer to this question

Answers
Answer: A
Step-by-step explanation: hope this helps!
please give brainliest!
Answer:
A. Michael must get a degree in engineering LOLLLLL