Find x when y = 2 for the following equation: y = 6x + 8
PLS HELP ASAP
Answers
2 = 6x + 8
2-8 = 6x
6x = -6
x = -1
Related Questions
find two numbers whose difference is 164 and whose product is a minimum.
Answers
Answer: The lowest possible product would be -6724 given the numbers 82 and -82.
We can find this by setting the first number as x + 164. The other number would have to be simply x since it has to have a 164 difference.
Next we'll multiply the numbers together.
x(x+164)
x^2 + 164x
Now we want to minimize this as much as possible, so we'll find the vertex of this quadratic graph. You can do this by finding the x value as -b/2a, where b is the number attached to x and a is the number attached to x^2
-b/2a = -164/2(1) = -164/2 = -82
So we know one of the values is -82. We can plug that into the equation to find the second.
x + 164
-82 + 164
82
Step-by-step explanation: Hope this helps.
Help me on this one please

Answers
Answer:
Choice D
Step-by-step explanation:
Choices A and B does not imply Dilation but Translation. Though Choice C implies Dilation, but it implies that \(\triangle J'K'L'\) is half the size of \(\triangle JKL\) but we can see that \(\triangle J'K'L'\) is larger than \(\triangle JKL\) so Choice D.
a particular highway has an average of 8 potholes per mile. what is the probability of a driver encountering 7 potholes in a given mile?
Answers
The probability of a driver encountering 7 potholes in a given mile of a highway with an average of 8 potholes per mile can be calculated using the Poisson distribution. The probability of encountering exactly 7 potholes is approximately 0.145.
The Poisson distribution is a statistical distribution that can be used to calculate the probability of a certain number of events occurring in a fixed interval of time or space, given the average rate of occurrence. In this case, the average rate of potholes per mile is 8. The Poisson distribution formula is:
P(X = x) = (e^(-λ) * λ^x) / x!
where P(X = x) is the probability of x events occurring, e is the base of the natural logarithm, λ is the average rate of occurrence, and x! is the factorial of x.
To calculate the probability of encountering exactly 7 potholes in one mile of the highway, we substitute λ = 8 and x = 7 into the formula:
P(X = 7) = (e^(-8) * 8^7) / 7!
≈ 0.145
Therefore, the probability of encountering exactly 7 potholes in one mile of the highway is approximately 0.145 or 14.5%
To learn more about Poisson distribution here:
brainly.com/question/17280826#
#SPJ11
Please give a real answer.
No Docs/No files/No link
I will rate a 5-star and give the brainiest.

Answers
Answer:
3.5 m
Step-by-step explanation:
PQ = 5/(5+5) × 7
= 5/10 × 7
= 3.5 m
Mr. Nieto has to pay an income tax of
15% on earned wages of $25,500. How
much money will Mr. Nieto spend to pay the
income tax?
F $382.50 H $3,825.00
G $25,882.50 J $29,325.00

Answers
Answer:
The answer is (H) because you multiply 25,500 by 15% hope its right.
Step-by-step explanation:
A line passes through the points (3,20) and (9,26). Write a linear function rule in terms of x and y for this line.
Answers
Answer:
y = x + 17
Step-by-step explanation
there are 40 rows of seats in a class.Each row has 120 chairs.How many students can sit in the class?
Answers
Answer:
4800 students
Step-by-step explanation:
120x40=4800students
4800 can sit in the class
Help pleaseeeeeeeee
...

Answers
Answer:
The answer is $2.04 i dont know what the silver coin is.
Step-by-step explanation:
Liz makes footprints in the snow with her boots that are \blueD{\dfrac34}
4
3
start color #11accd, start fraction, 3, divided by, 4, end fraction, end color #11accd foot long. Liz's feet are only \greenD{\dfrac23}
3
2
start color #1fab54, start fraction, 2, divided by, 3, end fraction, end color #1fab54 foot long.
What expression can be used to find out how much longer Liz's boot prints are than her feet?
Answers
The expression can be used for much longer Liz's boot prints are than her feet is 9/12 - 8/12.
What is an expression?Expressions are defined as mathematical statements that have a minimum of two terms containing variables or numbers.
Given that,
Liz makes footprints in the snow with her boots that are 3/4 and 2/3
To determine expression can be used to much longer Liz's boot prints are than her feet
The difference between 3/4 and 2/3 as :
⇒ 3/4 - 2/3
Dividing and multiplying by 12 in the above expression,
⇒ 3/4 - 2/3
⇒ (3/4 - 2/3)12/12
⇒ 3*3/12 - 2*4/12
⇒ 9/12 - 8/12
Learn more about Expressions here:
brainly.com/question/13947055
#SPJ1
Solve system of equation using elimination by addition.
Will give brainliest!!

Answers
Answer:
x = 2
y = -1
Step-by-step explanation:
You can add together the equations so the x term cancels out:
-3x + 5y = -11
+ (3x + 7y = -1)
The -3x and 3x cancel out, 5y and 7y add to 12y, and -11 and -1 add to -12:
12y = -12
Divide by 12 on both sides to get
y = -1
We can substitute this value into one of the equations to solve for x:
3x + 7y = -1
3x +7(-1) = -1
3x - 7 = -1
3x = 6
x = 2
help meeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee

Answers
Answer: 9.7 seconds
Step-by-step explanation:
\(16t^2=1503\\\\t^2 =\frac{1503}{16}\\\\t=\sqrt{1503/16} \text{ } (t > 0)\\\\t \approx 9.7\)
Consider the following ordered pairs that represent a relation.
{(-4,-7), (0, 6), (5,-3), (5,2)}
What can be concluded of the domain and range for this relation? Check all that apply.
The domain is the y values of the ordered pairs.
The range is the set of output values.
The given relation is a function.
Zero is included in the range of the relation.
5 is included in the domain of this relation,
Answers
==========================================
Explanation:
Choice A is false because the domain consists of the x values, not the y values. The domain is the set of allowed inputs.Choice B is true because the range is the set of possible output y values.Choice C is false because the input x = 5 leads to multiple outputs (y = -3 and y = 2 at the same time). Plotting all the points on the same xy grid shows the relation fails the vertical line test.Choice D is false because y = 0 is not in any of the points. Choice E is true since x = 5 is part of (5,-3) and (5,2)Answer:
The answers are B.) The range is the set of output values. and E.)
5 is included in the domain of this relation.
Step-by-step explanation:
This is right on edg. 2020
pls help me :"( geometry i will give brainliest
and 100 Pts

Answers
Answer:
ΔLNM is proved as isosceles triangle. Below for explanation.
Step-by-step explanation:
We know that:
AMBX = SquareSquares have equal sidesSince AMBX is a square, AL must equal to BN because they are the extra lengths of the square. The lengths of the square are AM, MB, BX, XA.
Side of square + Extra length = Side of triangleThis can tell us that the two sides of the triangle are equal. We also know that if 2 sides of a triangle are equal, it is classified as an isosceles triangle. Hence, ΔLNM is proved as an isosceles triangle.
Hoped this helped!
Answer:
ΔLNM is proved as isosceles triangle
Step-by-step explanation:
5/16 with bar notation
Answers
Answer:
5/16 with bar notation is written as 0.3125, where the bar is placed over the digit "5" to indicate that it repeats infinitely. This notation is used to represent a repeating decimal, where the digit or group of digits after the bar repeats infinitely without terminating. In this case, the digit "5" repeats infinitely after the decimal point.
Answer:
The bar notation is used to indicate that a digit or a sequence of digits repeats indefinitely. To express 5/16 with a bar notation, we need to find the decimal equivalent of 5/16 and identify any repeating digits.
To convert 5/16 to a decimal, we can perform the division as follows:
0.3125
The decimal equivalent of 5/16 is 0.3125. Since there are no repeating digits, we cannot express it with a bar notation.
When asked to find the value of x for
which f(x)=17, Danny answered 39. What
mistake did Danny make? What is the
correct answer?
Answers
Answer and Step-by-step explanation:
We are not given the function in question, but in order to explain, will form a function. Suppose f(x) = 3x + 2.
If f(x) = 17, then
3x + 2 = 17, to find the value of x, we have solve for x in the equation.
3x = 17 – 2
3x = 15
x = 5
This is the method that can be used to solve problems of this nature.
if T=1/4 A^3B make A the subject of formula
Answers
Step-by-step explanation:
A³B = 4T
A³=4T/B
A = cbrt 4T/B. or
³√(4T/B)
hope this helps.
The measures of the legs of a right triangle both measure 7 yards. What is the length of the hypotenuse? Round your answer to the nearest tenth.
Answers
\( {a}^{2} + {b}^{2} = {c}^{2} \)
\( {7}^{2} + {7}^{2} = {98}^{2} \)
\( \sqrt{98} = 9.9 \: yards\)
(PLEASE HELP ME ASAP)
Write down a number that has a value less than |4.7|
Answers
Answer:
4.6
Step-by-step explanation:
3.. litteraly anything less than that
Answer:
0
Step-by-step explanation:
|4.7| = 4.7
Any number less than a positive 4.7 is less than |4.7|.
help i don't get this algebra

Answers

Select the interval where f is negative.
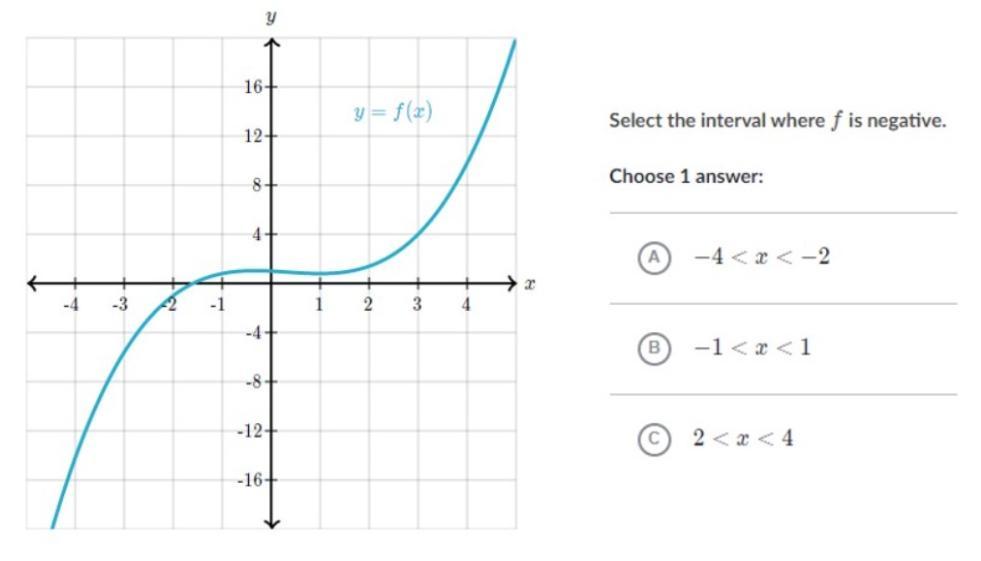
Answers
Answer: A
Step-by-step explanation:
Based on the graph, we know that it is negative if it is under the x-axis. It is also indicated by the negative labels.
A: correct
Looking at choice A, it says the interval is from -4<x<-2. This means we have to find x=-4 and x=-2. On the graph, that interval is below the x-axis, so it is negative.
B: incorrect
Looking at choice B, it says the interval is from -1<x<1. This means we have to find x=-1 and x=1. On the graph, that interval is above the x-axis, so it is positive, not negative.
C: incorrect
Looking at choice C, it says the interval is from 2<x<4. This means we have to find x=2 and x=4. On the graph, that interval is above the x-axis, so it is positive, not negative.
Therefore, A is the correct answer.
A small airplane coming in for a landing descends 5 over 66 miles per minute. About how long does it take to descend 4,000 feet? Show all work. Please.
Answers
Therefore, it takes the airplane about 10 minutes to descend 4,000 feet.
What is distance?Distance refers to the length or extent of space between two points or objects. It is a measure of how far apart two points are, and is typically measured in units such as meters, kilometers, miles, or feet. Distance is a scalar quantity, which means it only has a magnitude (i.e., a numerical value) and no direction associated with it. It is often used in calculations involving speed, time, and other physical quantities.
by the question.
We can use the rate of descent given in miles per minute to calculate the time it takes to descend a certain distance. First, let's convert 5/66 miles per minute to feet per minute:
5/66 miles per minute * 5280 feet per mile = 400 feet per minute
So, the airplane descends at a rate of 400 feet per minute. To find the time it takes to descend 4,000 feet, we can use the formula:
time = distance / rate
Plugging in the values we know:
time = 4000 feet / 400 feet per minute = 10 minutes
To learn more about rate:
https://brainly.com/question/14731228
#SPJ1
Which of the following is NOT a guideline for finding the best multiple regression equation? Choose the correct answer below. A. If two predictor values have a very high linear correlation coefficient, both should be included in finding the multiple regression equation. B. Consider equations with high values of adjusted R2, and try to include only a few variables C. Consider the P-value to select an equation having overall significance. D. Use common sense and practical considerations to include or exclude variables.
Answers
Answer: Answer A is correct :)
Step-by-step explanation:
If two predictor values have a very high linear correlation coefficient, both should be included in finding the multiple regression equation.
find teh exact value of sin 2x given that sec x = 3/2 and csc y = 3 and x and y are in quadrant 1
Answers
The exact value of \(sin 2x\) is \(4√5/9.\)
Given that \(sec x = 3/2 and csc y = 3\)where x and y are in the 2x = 2 sin x quadrant, we need to find the exact value of sin 2x.
In the first quadrant, we have the following values of the trigonometric ratios:\(cos x = 2/3 and sin y = 3/5\)
Also, we know that sin \(2x = 2 sin x cos x.\)
Now, we need to find sin x.
Having sec x = 3/2, we can use the Pythagorean identity
\(^2x + 1 = sec^2xtan^2x + 1 = (3/2)^2tan^2x + 1 = 9/4tan^2x = 9/4 - 1 = 5/4tan x = ± √(5/4) = ± √5/2\)
As x is in the first quadrant, it lies between 0° and 90°.
Therefore, x cannot be negative.
Hence ,\(tan x = √5/2sin x = tan x cos x = √5/2 * 2/3 = √5/3\)
Now, we can find sin 2x by using the value of sin x and cos x derived above sin \(2x = 2 sin x cos xsin 2x = 2 (√5/3) (2/3)sin 2x = 4√5/9\)
Therefore, the exact value of sin 2x is 4√5/9.
To know more about trigonometric visit :
https://brainly.com/question/29156330
#SPJ11
if the point p falls on the unit circle and has an x coordinate of 5/13 find the y coordinate of point p
Answers
To find the y-coordinate of point P on the unit circle, given that its x-coordinate is 5/13, we can utilize the Pythagorean identity for points on the unit circle.
The Pythagorean identity states that for any point (x, y) on the unit circle, the following equation holds true:
x^2 + y^2 = 1
Since we are given the x-coordinate as 5/13, we can substitute this value into the equation and solve for y:
(5/13)^2 + y^2 = 1
25/169 + y^2 = 1
To isolate y^2, we subtract 25/169 from both sides:
y^2 = 1 - 25/169
y^2 = 169/169 - 25/169
y^2 = 144/169
Taking the square root of both sides, we find:
y = ±sqrt(144/169)
Since we are dealing with points on the unit circle, the y-coordinate represents the sine value. Therefore, the y-coordinate of point P is:
y = ±12/13
So, the y-coordinate of point P can be either 12/13 or -12/13.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
My square patio is tiled with square tiles, all the same size. All the tiles are gray, except the tiles along the two diagonals, which are all yellow. (The corners are yellow, the center is yellow, and all the tiles along the diagonal in between are yellow.) If there are $89$ yellow tiles, how many gray tiles are there
Answers
Answer:
1936
Step-by-step explanation:
We can start by removing the center tile, because all four diagonals over lap on that tile. We'll add it back later. 88/4=22. which means there are 22 tiles per half, 44+1(the center tile) total tiles per side, which means there are a total of 1936 tiles.
AOPS ANSWER:
Suppose that we have a square with dimensions \($e \times e$\). The diagonals each have \($e$\\\) tiles. If \($e$\\\) is even, the number of yellow tiles is \($2e$\), because the \(2\) diagonals don't intersect. If \($e$\) is odd, then the number of yellow tiles is \($e+e-1=2e-1$\). (We have to subtract \(1\) because the center tile is counted \(2\) times). We know that there are \(89\) yellow tiles, which is an odd number, so \($89=2e-1$\). This implies that \($e = 45$\). So the dimensions of the floor are \($45 \times 45$\), or \(2025\\\) square units. Since all of the other tiles are gray, there are \($2025-89=\boxed{1936}$\) gray tiles.
Ihis assignment contributes \( 40 \% \) to your year mark. Question 1 Find \( \frac{d y}{d x} \) if 1.1. \( y=\sinh ^{-1}\left(\cos ^{2} x\right) \). 1.2. \( x^{2}+y^{2}=x y \). \( 1.3 \quad y=\left(\
Answers
1.1. \(\frac{dy}{dx} = -2cos(x)sinh(cos^{2}x)\)
1.2. \(\frac{dy}{dx} = \frac{2x-y}{y-x}\)
1.3. \(\frac{dy}{dx} = \frac{3x^{2} -2xy+5x}{2y-3x+1}\)
1.1. To find \(\frac{dy}{dx}\) for \(y = sinh^{-1}(cos^{2}x )\), we need to apply the chain rule. The derivative of \(sinh^{-1}(u)\) is \(\frac{1}{\sqrt{1+u^{2} } }\), and the derivative of \(cos^2(x)\) is \(-2cos(x)sin(x)\). Therefore, we have:
\(\frac{dy}{dx} = \frac{d}{dx}(sinh^{-1}(cos^{2}(x) ) )\\ = \frac{1}{\sqrt{1+cos^{4}(x) } }.\frac{d}{dx}(cos^{2}(x) )\\ = -2cos(x)sinh(cos^{2}(x) )\)
1.2. To find \(\frac{dy}{dx}\) for \(x^{2} +y^{2} = xy\), we can differentiate both sides of the equation implicitly.
Applying the product rule and chain rule, we get:
\(2x+2yy' = y+xy'\)
Rearranging the equation and solving for \(\frac{dy}{dx}\), we have:
\(\frac{dy}{dx} = \frac{2x-y}{y-x}\)
1.3. To find \(\frac{dy}{dx}\) for \(y = \frac{x^{3}-2x^{2} +5x }{2y-3x+1}\), we need to differentiate both sides of the equation implicitly. Applying the quotient rule and chain rule, we get:
\(\frac{2y-3x+1}{2}.\frac{dy}{dx} = \frac{(3x^{2} -4x+5)(2y-3x+1)-(x^{3}-2x^{2} +5x )(2-3y)}{(2y-3x+1)^{2} }\)
Simplifying the equation and solving for \(\frac{dy}{dx}\), we have:
\(\frac{dy}{dx} = \frac{3x^{2} -2xy+5x}{2y-3x+1}\)
The derivatives \(\frac{dy}{dx}\) for the given equations are:
1.1. \(\frac{dy}{dx} = -2cos(x)sinh(cos^{2}x)\)
1.2. \(\frac{dy}{dx} = \frac{2x-y}{y-x}\)
1.3. \(\frac{dy}{dx} = \frac{3x^{2} -2xy+5x}{2y-3x+1}\)
To know more about chain rule visit
https://brainly.com/question/28350594
#SPJ11
Use your knowledge on the triangle proportionality theorem to find the missing side length indicated. Be sure to explain the proportion you used.

Answers
Answer:
? = 4.29
Step-by-step explanation:
Remark
Let x be the question mark. You get the proportionality by using the dimensions of the little triangle to the dimensions of the large triangle.
Equation
14/(14+ 4) = 15/(x + 15) Combine like terms on the left
14/18 = 15/(x + 15) Cross multiply
14*(x + 15) = 18 * 15 Simplify the right
14(x + 15) = 270 Divide by 14
x + 15 = 270 / 14
x + 15 = 19.29 Subtract 15 from both sides
x = 19.29 - 15
x = 4.29
For homework, Anya had to find the width of a bedroom after the scale changed from 1 inch : 4 feet to 1 inch : 7 feet. Her work is shown below.
1 inch = 4 feet. 1 inches = 7 feet. A rectangle with length of 4 inches and width of 2 inches. StartFraction 1 over 7 EndFraction = StartFraction x over 2 EndFraction. 7 x = 2. x = StartFraction 2 over 7 EndFraction feet.
1
7
= x
2
7x = 2x = 2
7
feet
What error did Anya make?
Answers
Answer:
she set up the proportion incorrectly; the second ratio should be 2/x
Step-by-step explanation:
To obtain the width :
Scale drawing :
Initial = 1 inch = 4 feet
New = 1 inch = 7 feet
Width of rectangle = 2 inches
New width should be in the form :
new scale = width of rectangle / width of drawing
If width of drawing = x
1 / 7 = 2 / x
Cross multiply
x = 7*2
x = 14
Answer:
its A
Step-by-step explanation:
Solve each algebraic equation for the indicated variable
10r - 20 = 5r + 35
Answers
Answer:
r=11
Step-by-step explanation:
10r - 20 = 5r + 35
-5r. -5r
---------------------------
5r - 20 = 35
+20 = +20
---------------------------
5r = 55
------------
5r. 5
r=11
HI GUYS PLEASE HELPP, PLEASE!!!
THANKS SO MUCH FOR THE HELP TO WHOEVER HELPED
PLEASE BE RELEVANT!!
3. Determine the final price of purchasing a bouquet of flowers at $12.99 by first applying a coupon of 12% and then adding the sales tax of 13%.
Answers
Answer:‘12.92
Step-by-step explanation:
Answer:
Step-by-step explanation:
$12.99
applying coupon
\(12.99(1-12\%) = 12.99*88\% = 11.4312\\11.4312 * (1+13\%) = 12.917=12.92\)