Find two values of Θ, 0< Θ < 2 pi, that satisfy the following equationsin Θ = negative square root 2 over 2

Answers
Given:
\(\sin\theta=-\frac{\sqrt{2}}{2},0\leq\theta<2\pi\)To find:
The two values.
Explanation:
It can be written as,
\(\begin{gathered} \sin\theta=-\frac{\sqrt{2}}{2}\times\frac{\sqrt{2}}{\sqrt{2}} \\ \sin\theta=-\frac{2}{2\sqrt{2}} \\ \sin\theta=-\frac{1}{\sqrt{2}} \\ \theta=\sin^{-1}(-\frac{1}{\sqrt{2}}) \end{gathered}\)Since the angle lies between 0 and 2π.
Also, the value of the sine function is negative only when the angle lies in the third and fourth quadrant.
So, the angles are,
\(\begin{gathered} \theta=180+45^{\circ}\Rightarrow\text{ }225^{\circ}\text{ }(or)\text{ }\frac{5\pi}{4} \\ \theta=360-45\Rightarrow\text{ }315^{\circ}\text{ }(or)\text{ }\frac{7\pi}{4} \end{gathered}\)Final answer:
The values are,
\(\theta=\frac{5\pi}{4},\frac{7\pi}{4}\)Related Questions
e) A student spent 50 minutes doing her homework. She spent m minutes doing Geography. 2m minutes doing Mathematics and the remaining (m + 7) minutes studying History. How many minutes did she spend doing Mathematics?
Answers
Answer: 22 minutes
Step-by-step explanation: m + 2m + m + 7 = 4m + 7
4m + 7 = 50
4m = 44
m = 11
2m = 11 x 2 = 22 minutes
A market research company was interested in comparing three communities A, B and C to determine whether there are any differences in their use of water filters in homes. Each of 100 homeowners sampled from each community was asked whether or not they have installed water-filtering system in their homes. Their responses (Yes or No) are summarized in the following contingency table.
Use Filters
Community | Yes | No
A 62 38
B 58 42
C 73 27
a) Clearly state the null and alternative hypotheses in this problem.
b) Calculate the expected count for the bottom right cell (i.e., Community ‘C’ and ’No’), and explain what the number means.
c) The Chi-square statistic has been calculated to be 13.22. What can we conclude from this finding?
Answers
a) The null hypothesis is that there is no difference in the proportion of homeowners using water filters among the three communities. The alternative hypothesis is that at least one community has a different proportion of homeowners using water filters than the other communities.
b) To calculate the expected count for the bottom right cell, we can use the formula:
Expected count = (row total x column total) / grand total
The row total for Community C and the column total for No are both 100, and the grand total is 300. Therefore:
Expected count = (100 x 100) / 300 = 33.33
The expected count of 33.33 for the bottom right cell means that if there were no difference in the proportions of homeowners using water filters among the three communities, we would expect 33.33 of the 100 homeowners in Community C to answer 'No' to the question about water filters.
c) To determine what we can conclude from the Chi-square statistic of 13.22, we need to compare it to the critical value for a Chi-square distribution with (3-1) x (2-1) = 2 degrees of freedom at the desired level of significance. Let's assume a level of significance of 0.05. From a Chi-square distribution table, the critical value with 2 degrees of freedom at 0.05 level of significance is 5.99.
Since 13.22 is greater than 5.99, we can reject the null hypothesis and conclude that there is a significant difference in the proportion of homeowners using water filters among the three communities. However, we cannot determine from this test alone which communities have different proportions of homeowners using water filters. We would need to conduct further tests, such as post-hoc tests, to investigate the specific differences among the communities.
Bound
Figure 2.
Jenny would like to buy a new air conditioner for his home. As seen in Figure 2 above he has
3 types of brands that he can consider. The cash price for Daewoo is RM1,899, Daikin at a
price of RM1,699 and last choice is Mitsubishi at a price of RM1.999. He plans to make 18
monthly instalments, if he pays RM300 as a down payment for the air conditioner that he would
like to buy, find the interest charge for each brand if the interest rate is 4% based on originall
balance if he chooses to buy from Daikin, find the monthly instalment price and instalment
price that he needs to pay.

Answers
if Jenny chooses to buy from Daikin, the monthly installment price would be approximately RM98.89, and the total installment price to be paid would be approximately RM1,779.98 (18 monthly installments * RM98.89).
How to determine the monthly instalment price and instalment price that Daikin needs to pay.Calculating the loan amount for each brand by subtracting the down payment from the cash price:
Loan amount for Daewoo = RM1,899 - RM300 = RM1,599
Loan amount for Daikin = RM1,699 - RM300 = RM1,399
Loan amount for Mitsubishi = RM1,999 - RM300 = RM1,699
Calculating the interest charge for each brand:
Interest charge for Daewoo = Loan amount for Daewoo * Interest rate = RM1,599 * 0.04 = RM63.96
Interest charge for Daikin = Loan amount for Daikin * Interest rate = RM1,399 * 0.04 = RM55.96
Interest charge for Mitsubishi = Loan amount for Mitsubishi * Interest rate = RM1,699 * 0.04 = RM67.96
To find the monthly installment price, divide the total amount (cash price + interest charge) by the number of monthly installments:
Monthly installment price for Daewoo = (Cash price of Daewoo + Interest charge for Daewoo) / Number of monthly installments = (RM1,899 + RM63.96) / 18 ≈ RM107.22
Monthly installment price for Daikin = (Cash price of Daikin + Interest charge for Daikin) / Number of monthly installments = (RM1,699 + RM55.96) / 18 ≈ RM98.89
Monthly installment price for Mitsubishi = (Cash price of Mitsubishi + Interest charge for Mitsubishi) / Number of monthly installments = (RM1,999 + RM67.96) / 18 ≈ RM116.72
Therefore, if Jenny chooses to buy from Daikin, the monthly installment price would be approximately RM98.89, and the total installment price to be paid would be approximately RM1,779.98 (18 monthly installments * RM98.89).
Learn more about monthly installment at https://brainly.com/question/3260195
#SPJ1
A customer purchased 8 pairs of socks at the same price each. The customer had $42 to spend on clothing. After purchasing the socks, the customer was left with $17.68. How much did each pair of socks cost? Enter your answer in the box.
Answers
Answer:
3.04
Step-by-step explanation:
Let x be the cost of each pair
42 - 8x = 17.68
-8x = -24.32
8x = 24.32
x = 3.04
what is 999.09344471 rounded to the nearest square kilometer?
Answers
The nearest kilometers to 999.09344471 km is 1000 km.
Given value is 999.09344471 Km.
We have to calculate the round off value to the nearest kilometers. we know that after the decimal if the value of tenth place is 5 or bigger than 5 then we add 1 to the tens place digit, this is the fundamental rule of rounding off.
Now on following this rule from the very right hand side up to the tenth place digit we come to the conclusion that only the value after the decimal (934) is to be rounded off which is (900).
So 999.09344471 km is finally becomes 999.900 km after rounding of to nearest hundredth value.
Again rounding off 999.900 km to nearest km so it becomes 1000 km.
The nearest kilometers to 999.09344471 km is 1000 km.
For more details on round off follow the link:
brainly.com/question/1093198
The entire pink figure has been transformed to create the new blue image. Describe the transformation that has taken place.

Answers
Answer:
D. (bottom right)
Step-by-step explanation:
If there is a line where y = x, that means that y and x can both equal 1, 2, 3, -1, -2, -3, etc. They are just always the same. This line, then, would pass through (just for example) (-4, -4) and (4, 4). If you reflect the pink figure across that line, you will get the blue figure. Hope this helps!
(-2,-3), (4,3) in point slope form
Answers
Answer: y + 3 = 1 ⋅ (x + 2)
Step-by-step explanation:
Evaluate the definite integral of sin^5(x)dx from 0 to pi/2.
Answers
Step-by-step explanation:
The definite integral of sin^5(x)dx from 0 to pi/2 can be evaluated using the method of substitution.
Let u = sin(x), then du = cos(x)dx
The integral becomes:
∫sin^5(x)dx = ∫u^5du from 0 to sin(π/2)
= (u^6)/6 evaluated at sin(π/2) and 0
= (sin^6(π/2))/6 - 0
= (1^6)/6
= 1/6
So, the definite integral of sin^5(x)dx from 0 to pi/2 is equal to 1/6.
Solve the following system of equations using the substitution method.
y=3x-10
3y-x=2
Answers
3(3x-10)-x=2 distribute
9x-30-x=2 Combine 9x with -x and add 30 to each side.
8x=32 divide 8 each side
x=4, now plug x=4 into y=3x-10 and solve for y
y=3(4)-10
y=12-10
y=2
Answer: x=4 and y=2
According to a survey conducted by the Association for Dressings and Sauces, 80% of American adults eat
salad once a week. A nutritionist suspects that this percentage is not accurate. She conducts a survey of
445 American adults and finds that 374 of them eat salad once a week. Use a 0.005 significance level to
test the claim that the proportion of American adults who eat salad once a week is equal to 80%.
Claim: Select an answer which corresponds to [Select an answer
Opposite: Select an answer which corresponds to [Select an answer
The test is: Select an answers
The test statistic is: z-
(to 2 decimals)
The Critical Value is: z-
Based on this we: [Select an answer
Conclusion: There Select an answer appear to be enough evidence to support the claim that the
proportion of American adults who eat salad once a week is equal to 80%.
Answers
Since the test statistic (2.53) falls within the critical values (-2.576 and 2.576), we fail to reject the null hypothesis.
How to solveTo test the claim that the proportion of American adults who eat salad once a week is equal to 80%, we will conduct a hypothesis test.
Claim: p = 0.80
Opposite: p ≠ 0.80
The test is a two-tailed z-test.
Sample proportion (p) = 374/445 = 0.8404
Test statistic= (0.8404 - 0.80) / sqrt((0.80 * (1 - 0.80)) / 445)
z = 2.53 (rounded to 2 decimals)
Significance level (α) = 0.005, so the critical values for a two-tailed test are -2.576 and 2.576.
Since the test statistic (2.53) falls within the critical values (-2.576 and 2.576), we fail to reject the null hypothesis.
Conclusion: There does not appear to be enough evidence to reject the claim that the proportion of American adults who eat salad once a week is equal to 80%.
Read more about test statistic here:
https://brainly.com/question/15110538
#SPJ1
Was it evaluated correct?
explain your reasoning

Answers
Answer:
Yes
Step-by-step explanation:
Yes. They did exponents and grouping symbols first, then multiplication and division left to right. Addition came before multiplication and division because it was inside a grouping symbol.
Suppose in Florida it was observed that 70% of parents who were vegetarian were succeeded by children who were vegetarian and 30% by non-vegetarian. Also, 40% of non-vegetarians were succeeded by vegetarians and 60% by non-vegetarians. Set up the 2x2 stochastic matrix with columns and rows labeled V and NV that describes this situation.
V NV
A. V 0.7 0.4
NV 0.3 0.6
V NV
B. V 0.4 0.7
NV 0.3 0.6
V NV
C. V 0.7 0.4
NV 0.7 0.6
V NV
D. V 0.6 0.3
NV 0.3 0.4
Answers
Answer:
A
Step-by-step explanation:
From the information given:
To create the required stochastic matrix, we need to take parents who are shown to be vegetarian or nonvegetarian in the column and the children who are vegetarian or nonvegetarian into the row section.
So;
Vegetarian V → 70% → nonvegetarian NV → 30%
nonvegetarian NV → 40% vegetarian V → 60%
V NV
The 2x2 stochastic matrix = \(\left \Big { {{V} \atop {NV}} \right.} \left [\begin{array} {cc}0.7&0.4\\0.3&0.6\\\end{array}\right]\)
7. Kelly developed a formula for using a computer to find for a specific quote within a large set of articles.
The following function gives the length of the search, in seconds, over a set of n articles.
S(n) = 1.6 In (0.8n). What is the instantaneous rate of change of the search length for a set of 12 article:
Use correct units to explain the meaning of the answer.
Answers
instantaneous rate of change of the search length 0.1667 seconds per
How to find the instantaneous rate of change?We need to take the derivative of the function S(n) with respect to n and evaluate it at n=12 in order to determine the instantaneous rate of change of the search length for a set of 12 articles.
Taking the derivative of S(n) with respect to n using the chain rule, we get:
S'(n) = 1.6 * (1/(0.8n)) * 0.8 = 2/n
Evaluating this expression at n=12, we get:
S'(12) = 2/12 = 0.1667 seconds per article
This indicates that the search time will increase by approximately 0.1667 seconds per article if the set contains 12 articles by one unit. Alternately, the search time per article will decrease by approximately 0.1667 seconds if the set's number of articles decreases by one unit from 12.
Therefore, the units for the instantaneous rate of change are "seconds per article", indicating the change in search time for each additional or fewer article in the set.
know more about rate of change visit
https://brainly.com/question/12786410
#SPJ1
Natalia is a girl in a math class with a total of 11 girls and 9 boys. If the teacher selects one student at random to go to the board, what is the probability that Natalia will be selected?
A box of pens contains a total of 28 pens. If 4 of the pens are red and the rest are blue, what is the probability that the first pen pulled from the box will be red?
Katelyn has a package of 24 jelly beans. There are 9 cherry jelly beans in the package. What is the probability that the first jelly bean Katelyn pulls out of the package will be a cherry jelly bean?
A marble is drawn at random from a bag containing 2 blue marbles, 3 yellow marbles, and 7 orange marbles. What is the probability that the marble is not yellow and not blue?
(Five Stars & Thanks to whoever answers first)
Answers
Answer:
First, let's find how many students there are in total:
11 girls + 9 boys
= 20 students.
Out of those 20 students, we are trying to find the probability if Natalia will be selected first.
There is only one Natalia.
So, out of those students, the probability of selecting Natalia is a:
1/20 probability
(if wanted to convert into a percentage):
1/20 x 100
= 5% probability
Since we already know there are 28 given pens in total and 4 of them are red pens, there is a:
4/28 chance of selecting a red pen which can be simplified to a 1/7 probability.
(if wanted to convert into a percentage):
1/7 x 100
= 14% probability
Since we already know there are 24 jelly beans in total and 9 of them are cherry beans, there is a:
9/24 chance/probability of selecting a cherry jelly bean.
(if wanted to convert into a percentage):
9/24 x 100
= 37.5% probability
Let's first figure out how many marbles there are in total.
2 + 3 + 7
= 12 marbles in total.
Now let's exclude the marbles that are blue and yellow, leaving us with 7 orange marbles.
So the probability of selecting a marble that isn't blue/yellow is a:
7/12 probability
(if wanted to convert into a percentage)
7/12 x 100
= 58% probability
Calc II Question
Find the volume of the solid obtained by rotating the region bonded bt the given curves about the specified line.
Y = e^-x
Y = 1
X = 2
About the Y = 2
Answers
Answer:
\(\displaystyle \frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Step-by-step explanation:
This can be solved with either the washer (easier) or the shell method (harder). For the disk/washer method, the slice is perpendicular to the axis of revolution, whereas, for the shell method, the slice is parallel to the axis of revolution. I'll show how to do it with both:
Shell Method (Horizontal Axis)
\(\displaystyle V=2\pi\int^d_cr(y)h(y)\,dy\)
Radius: \(r(y)=2-y\) (distance from y=2 to x-axis)
Height: \(h(y)=2-(-\ln y)=2+\ln y\) (\(y=e^{-x}\) is the same as \(x=-\ln y\))
Bounds: \([c,d]=[e^{-2},1]\) (plugging x-bounds in gets you this)
Plugging in our integral, we get:
\(\displaystyle V=2\pi\int^1_{e^{-2}}(2-y)(2+\ln y)\,dy=\frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Washer Method (Parallel to x-axis)
\(\displaystyle V=\pi\int^b_a\biggr(R(x)^2-r(x)^2\biggr)\,dx\)
Outer Radius: \(R(x)=2-e^{-x}\) (distance between \(y=2\) and \(y=e^{-x}\))
Inner Radius: \(r(x)=2-1=1\) (distance between \(y=2\) and \(y=1\))
Bounds: \([a,b]=[0,2]\)
Plugging in our integral, we get:
\(\displaystyle V=\pi\int^2_0\biggr((2-e^{-x})^2-1^2\biggr)\,dx\\\\V=\pi\int^2_0\biggr((4-4e^{-x}+e^{-2x})-1\biggr)\,dx\\\\V=\pi\int^2_0(3-4e^{-x}+e^{-2x})\,dx\\\\V=\pi\biggr(3x+4e^{-x}-\frac{1}{2}e^{-2x}\biggr)\biggr|^2_0\\\\V=\pi\biggr[\biggr(3(2)+4e^{-2}-\frac{1}{2}e^{-2(2)}\biggr)-\biggr(3(0)+4e^{-0}-\frac{1}{2}e^{-2(0)}\biggr)\biggr]\\\\V=\pi\biggr[\biggr(6+4e^{-2}-\frac{1}{2}e^{-4}\biggr)-\biggr(4-\frac{1}{2}\biggr)\biggr]\)
\(\displaystyle V=\pi\biggr[\biggr(6+4e^{-2}-\frac{1}{2}e^{-4}\biggr)-\frac{7}{2}\biggr]\\\\V=\pi\biggr(\frac{5}{2}+4e^{-2}-\frac{1}{2}e^{-4}\biggr)\\\\V=\pi\biggr(\frac{5}{2}+\frac{4}{e^2}-\frac{1}{2e^4}\biggr)\\\\V=\pi\biggr(\frac{5e^4}{2e^4}+\frac{8e^2}{2e^4}-\frac{1}{2e^4}\biggr)\\\\V=\pi\biggr(\frac{5e^4+8e^2-1}{2e^4}\biggr)\\\\V=\frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Use your best judgment when deciding on what method you use when visualizing the solid, but I hope this helped!

Proving Triangles Congruent: ASA AAS

Answers
The congruence theorem required for each figure are
1. AAS
2. ASA
3. ASA
4. ASA
5. ASA
6. ASA
What is ASA congruence theorem?ASA (Angle-Side-Angle) congruence theorem states that if two triangles have two angles and the included side in common, then they are congruent.
That is to say, if two angles and the included side of one triangle are congruent to the corresponding two angles and included side of another triangle, then the two triangles are congruent.
AAS (Angle-Angle-Side) congruence theorem states that if two angles and a non-included side of one triangle are congruent to the corresponding angles and non-included side of another triangle, then the two triangles are congruent.
Learn more about ASA congruence theorem at:
https://brainly.com/question/2102943
#SPJ1
what is the value of x in the equation 8 (x+2.4)=105.6
Answers
distribute the 8 to the parenthesis, so 8x+19.2=105.6
-19.2
8x=86.4
/8
x=10.8
BIY
74
6+
84
3
-2 -1
D'
B
1
Which rule represents the translation from the pre-
image, ABCD, to the image, A'B'C'D'?
T₁-2(x, y)
OT₁,2(x, y)
T-2, 1(x, y)
OT2 1(x, y)
Answers
Answer:d
Step-by-step explanation:
The translation from the pre-image, Parallelogram ABCD, to the image, Parallelogram A'B'C'D' is T2, 1(x, y)
What is Graph?Graph is a mathematical representation of a network and it describes the relationship between lines and points.
The parallelogram ABCD is shifted to the right by 2 units and shifted up by 1 unit to get parallelogram A'B'C'D'.
Graph transformation is the process by which a graph is modified to give a variation of the proceeding graph.
The graphs can be translated or moved about the xy-plane.
This transformation rule is represented as:
(x,y) -> (x + 2,y + 1)
This transformation rule can be rewritten as:
T2, 1(x, y)
Hence, the translation from the pre-image, Parallelogram ABCD, to the image, Parallelogram A'B'C'D' is T2, 1(x, y)
To learn more on Graph click:
https://brainly.com/question/17267403
#SPJ5
20. Find the unknown angle measures.
51°
53°

Answers
The unknown angle measures are d = 76, c = 53, a = 51 and b = 76
Finding the unknown angle measures.From the question, we have the following parameters that can be used in our computation:
The lines
The sum of angles on a line is 180
So, we have
b = 180 - 51 - 53
b = 76
By vertical angle theorems, we have
d = 76
c = 53
a = 51
Read more about angles at
https://brainly.com/question/31898235
#SPJ1
Alex has a bag of marbles. 3 are blue, 5 are red, 12 are green, and 8 are purple. What is the probability of drawing 3 purple marbles in a row without replacement?
Answers
Rita has to carry 177 apples from a farm to the market. How many baskets will she need, given that each basket can hold 39 apples?
Answers
pls help me solve this

Answers
The results of operations between vectors are, respectively:
Case A: u + w = <- 3, - 1>
Case B: - 6 · v = <6, 6>
Case C: 3 · v - 6 · w = <- 21, - 15>
Case D: 4 · w + 3 · v - 5 · u = <39, 4>
Case E: |w - v| = √(4² + 3²) = 5
How to determine the operations between vectors
In this problem we must determine the operations between vectors, this can be done by following definitions:
Vector addition
v + u = (x, y) + (x', y') = (x + x', y + y')
Scalar multiplication
α · v = α · (x, y) = (α · x, α · y)
Norm of a vector
|u| = √(x² + y²)
Now we proceed to determine the result of each operation:
Case A:
u + w = <- 6, - 3> + <3, 2>
u + w = <- 3, - 1>
Case B:
- 6 · v = - 6 · <- 1, - 1>
- 6 · v = <6, 6>
Case C:
3 · v - 6 · w = 3 · <- 1, - 1> - 6 · <3, 2>
3 · v - 6 · w = <- 3, - 3> + <- 18, - 12>
3 · v - 6 · w = <- 21, - 15>
Case D:
4 · w + 3 · v - 5 · u = 4 · <3, - 2> + 3 · <- 1, - 1> - 5 · <- 6, - 3>
4 · w + 3 · v - 5 · u = <12, - 8> + <- 3, - 3> + <30, 15>
4 · w + 3 · v - 5 · u = <39, 4>
Case E:
|w - v| = |<3, 2> - <- 1, - 1>|
|w - v| = |<4, 3>|
|w - v| = √(4² + 3²) = 5
To learn more on vectors: https://brainly.com/question/31900604
#SPJ1
I will mark as the brainlest if correct

Answers
Answer:
Answer A
Step-by-step explanation:
A desk fan has blades of 4 inches rotated at a rate of 249 revolutions per minute.
Answers
The constraints of a problem are listed below. What are the vertices of the feasible region?
\(x+y\leq 7\\x-2y\leq -2\\x\geq 0\\y\geq 0\)
Answers
The vertices of the feasible region is (4, 3)
What are the vertices of the feasible region?From the question, we have the following parameters that can be used in our computation:
x + y ≤ 7
x - 2y ≤ -2
x ≥ 0
y ≥ 0
Express as equations
So, we have
x + y = 7
x - 2y = -2
Subtract the equations
3y = 9
So, we have
y = 3
Next, we have
x + 3 = 7
This gives
x = 4
Hence, the vertex of the feasible region is (4, 3)
Read more about linear programming at
https://brainly.com/question/14309521
#SPJ1
A research company desires to know the mean consumption of meat per week among people over age 29. A sample of 2092 people over age 29 was drawn and the mean meet consumption was 2.9 pounds. Assume that the standard deviation is known to be 1.4 pounds. Construct a 95% confidence interval for the mean consumption of meat among people over age 29. Round your answer to one decimal place.
Answers
Answer:
The 95% confidence interval for the mean consumption of meat among people over age 29 is between 2.8 pounds and 3 pounds.
Step-by-step explanation:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1-0.95}{2} = 0.025\)
Now, we have to find z in the Ztable as such z has a pvalue of \(1-\alpha\).
So it is z with a pvalue of \(1-0.025 = 0.975\), so \(z = 1.96\)
Now, find the margin of error M as such
\(M = z*\frac{\sigma}{\sqrt{n}}\)
In which \(\sigma\) is the standard deviation of the population and n is the size of the sample.
\(M = 1.96*\frac{1.4}{\sqrt{2092}} = 0.1\)
The lower end of the interval is the sample mean subtracted by M. So it is 2.9 - 0.1 = 2.8 pounds
The upper end of the interval is the sample mean added to M. So it is 2.9 + 0.1 = 3 pounds.
The 95% confidence interval for the mean consumption of meat among people over age 29 is between 2.8 pounds and 3 pounds.
Answer:
\(2.9-1.96\frac{1.4}{\sqrt{2092}}=2.84\)
\(2.9+1.96\frac{1.4}{\sqrt{2092}}=2.96\)
The confidence interval is given by \(2.84 \leq \mu \leq 2.96\)
Step-by-step explanation:
Information given
\(\bar X=2.9\) represent the sample mean
\(\mu\) population mean
\(\sigma =1.4\) represent the population standard deviation
n=2092 represent the sample size
Confidence interval
The confidence interval is given by:
\(\bar X \pm z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\) (1)
Since the Confidence interval is 0.95 or 95%, the significance is \(\alpha=0.05\) and \(\alpha/2 =0.025\), and the critical value would be \(z_{\alpha/2}=1.96\)
Replacing the info we got:
\(2.9-1.96\frac{1.4}{\sqrt{2092}}=2.84\)
\(2.9+1.96\frac{1.4}{\sqrt{2092}}=2.96\)
The confidence interval is given by \(2.84 \leq \mu \leq 2.96\)
The Blue Ridge parkway is 469 miles long. The parkway is a road that runs through 29 Virginia and North Carolina counties. Sam drove 2/5 of the parkway on vacation. How many miles did he drive? Simplify your answer and said it as a mixed number
Answers
187.6miles
Step-by-step explanation:
blue ridge parkway is 469miles
sam drove 2/5 of the parkway
2/5×469
=469×2/5
938/5
187.6miles
Select the correct answer. Which graph represents this inequality? 3x+y<1

Answers
Answer:
the answer is c the one above d
Step-by-step explanation:
what is the equation of the blue line
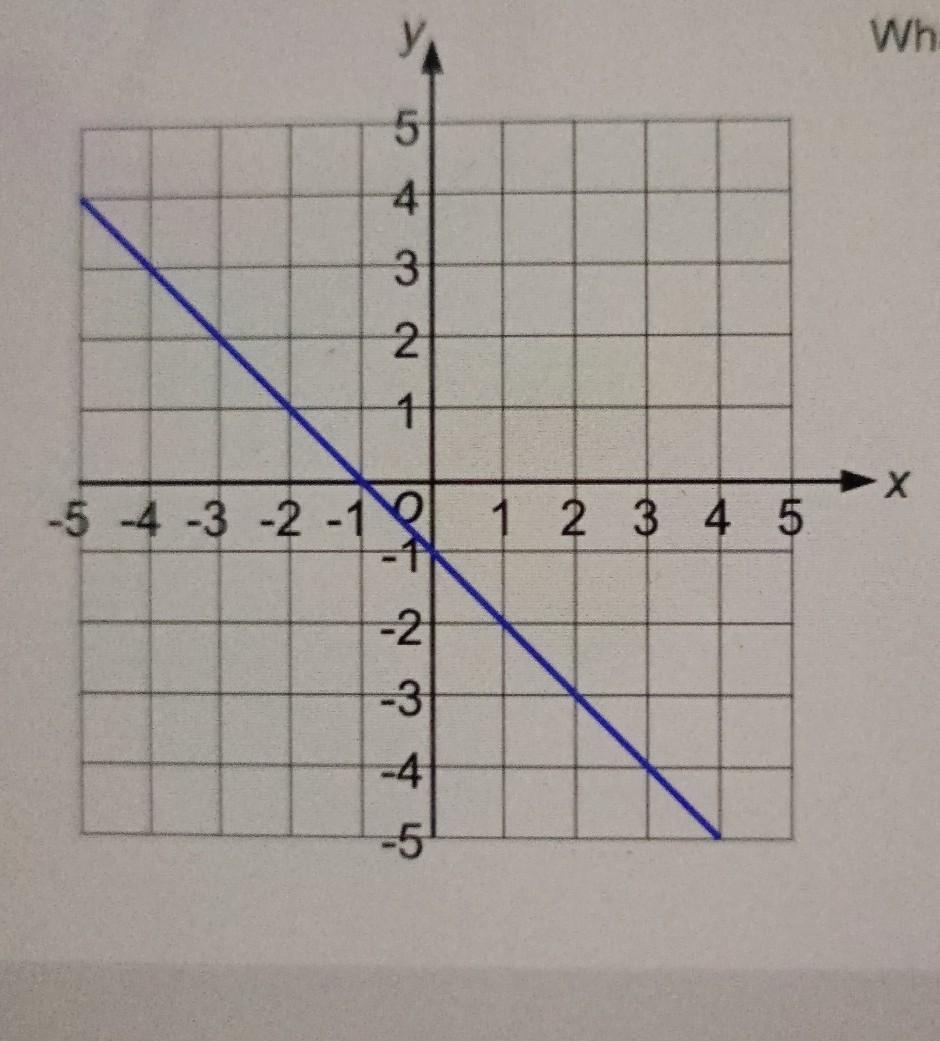
Answers
Answer: y+-1m -1
Step-by-step explanation:
how to solve this separable differential equation?

Answers
The solution to the differential equation \(2^{\sqrt{x}}\frac{dy}{dx} = cosce(ln(y))\) is,
\(\frac{y sin(ln(y))}{2} - \frac{y cos(ln(y))}{2} = C - \frac{2 ln(2) \sqrt{x} + 2}{ln^2(2)2^{\sqrt{x}}}\).
What is a differential equation?Any equation with at least one ordinary or partial derivative of an unknown function is referred to as a differential equation.
The given differential equation is \(2^{\sqrt{x}}\frac{dy}{dx} = cosce(ln(y))\).
Now, multiplying both sides by dx we,
\(2^{\sqrt{x}}dy = cosce(ln(y))dx\).
Dividing both sides by \(2^{\sqrt{x}}\) we have,
\(sin(ln(y))dy = \frac{dx}{2^{\sqrt{x}}}\).
\(\[ \int sin(ln(y))dy = \int \frac{dx}{2^{\sqrt{x}}}\).
\(\frac{y sin(ln(y))}{2} - \frac{y cos(ln(y))}{2} = C - \frac{2 ln(2) \sqrt{x} + 2}{ln^2(2)2^{\sqrt{x}}}\).
learn more about differential equations here :
https://brainly.com/question/14620493
#SPJ9