find the values of x for which the series converges. (enter your answer using interval notation.) [infinity]
∑ (x − 3)^n / 2n n = 0
Answers
Values of x for which the series converges are in the interval (1, 5).
A more detailed explanation of the answer.To find the values of x for which the series converges, we will use the Ratio Test. The series is given by:
∑ (x − 3)ⁿ / 2n, n = 0 to ∞
1. First, let's find the ratio of the (n+1)th term to the nth term:
((x - 3)ⁿ⁺¹ / 2ⁿ⁺¹) / ((x - 3)ⁿ / 2ⁿ) = (x - 3)ⁿ⁺¹ * 2ⁿ / (2ⁿ⁺¹ * (x - 3)ⁿ)
2. Simplify the ratio:
((x - 3)ⁿ⁺¹ / (x - 3)ⁿ) * (2ⁿ / 2ⁿ⁺¹) = (x - 3) * (1/2)
3. Apply the Ratio Test, the series converges if the absolute value of the ratio is less than 1:
| (x - 3) * (1/2) | < 1
4. Isolate x:
-2 < x - 3 < 2
5. Add 3 to all parts of the inequality:
1 < x < 5
Series converging values are in the interval (1, 5).
Learn more about Ratio Test.
brainly.com/question/15586862
#SPJ11
Related Questions
Can someone please identify the increasing interval?

Answers
Answer:
#4
Step-by-step explanation:
arrows on a graph means infinity
increase starts at 0,-1 infinity up to 1,4 infinity
gement System Grade 0.00 out of 10.00 (0%) Plainfield Electronics is a New Jersey-based company that manufactures industrial control panels. The equation gives the firm's production function Q=-L³+15
Answers
The equation Q = -L³ + 15 represents the production function of Plainfield Electronics, where Q is the quantity of industrial control panels produced and L is the level of labor input.
In this production function, the term -L³ indicates that there is diminishing returns to labor. As the level of labor input increases, the additional output produced decreases at an increasing rate. The term 15 represents the level of output that would be produced with zero labor input, indicating that there is some fixed component of output. To maximize production, the firm would need to determine the optimal level of labor input that maximizes the quantity of industrial control panels produced. This can be done by taking the derivative of the production function with respect to labor (dQ/dL) and setting it equal to zero to find the critical points. dQ/dL = -3L². Setting -3L² = 0, we find that L = 0.
Therefore, the critical point occurs at L = 0, which means that the firm would need to employ no labor to maximize production according to this production function. However, this result seems unlikely and may not be practically feasible. It's important to note that this analysis is based solely on the provided production function equation and assumes that there are no other factors or constraints affecting the production process. In practice, other factors such as capital, technology, and input availability would also play a significant role in determining the optimal level of production.
To learn more about Plainfield click here: brainly.com/question/30135800
#SPJ11
Isaac invested $1,800 in an account paying an interest rate of 4. 7% compounded
continuously. Assuming no deposits or withdrawals are made, how much money, to
the nearest hundred dollars, would be in the account after 15 years?
Answers
If no deposits and withdrawals are made then the amount that will be in the account after 15 years is $3642.84 .
In the question ,
it is given that ,
the amount invested is $1800 ,
the rate of interest = 4.7% = 0.047
time required is = 15 years
the continuous compounding formula is
y = P×\(e^{r \times t}\)
y = 1800*(\(e^{0.047 \times 15}\))
y = 1800*\(e^{0.705}\)
Simplifying further , we get
y = 1800*2.0238
y = 3642.84
Therefore , If no deposits and withdrawals are made then the amount that will be in the account after 15 years is $3642.84 .
Learn more about Continuous Compounding here
https://brainly.com/question/18324592
#SPJ4
URGENT !!!!!!! Please answer correctly !!!!!!!!!!!! Will be marking Brianliest !!

Answers
Answer:
A=79.2\(in^{2}\)
Step-by-step explanation:
A=a+b/2*h
A=5.4+14.4/2*8
A=19.8/2*8
A=9.9*8
A=79.2
Reaching out 2 standard errors on either side of the sample proportion makes us about _________ confident that the true proportion is capable within the interval
a. 90%
b. 99%
c. 95%
d. 68%
Answers
The correct answer is option c. 95%. Reaching out two standard errors on either side of the sample proportion gives us an interval of 95% confidence.
This is due to the fact that two standard errors on either side of the sample proportion will cover around 95% of the population's cases.
We can typically determine the true proportion in the population using this range of two standard errors on either side of the sample proportion.
This is because it helps us identify any potential outliers in the population and provides a range of population proportions for which we may be 95% certain.
We are 95% certain that the true percentage is capable inside the interval if we stretch out two standard errors on either side of the sample proportion.
To learn more about proportion visit:
https://brainly.com/question/1496357
#SPJ4
please help with my math
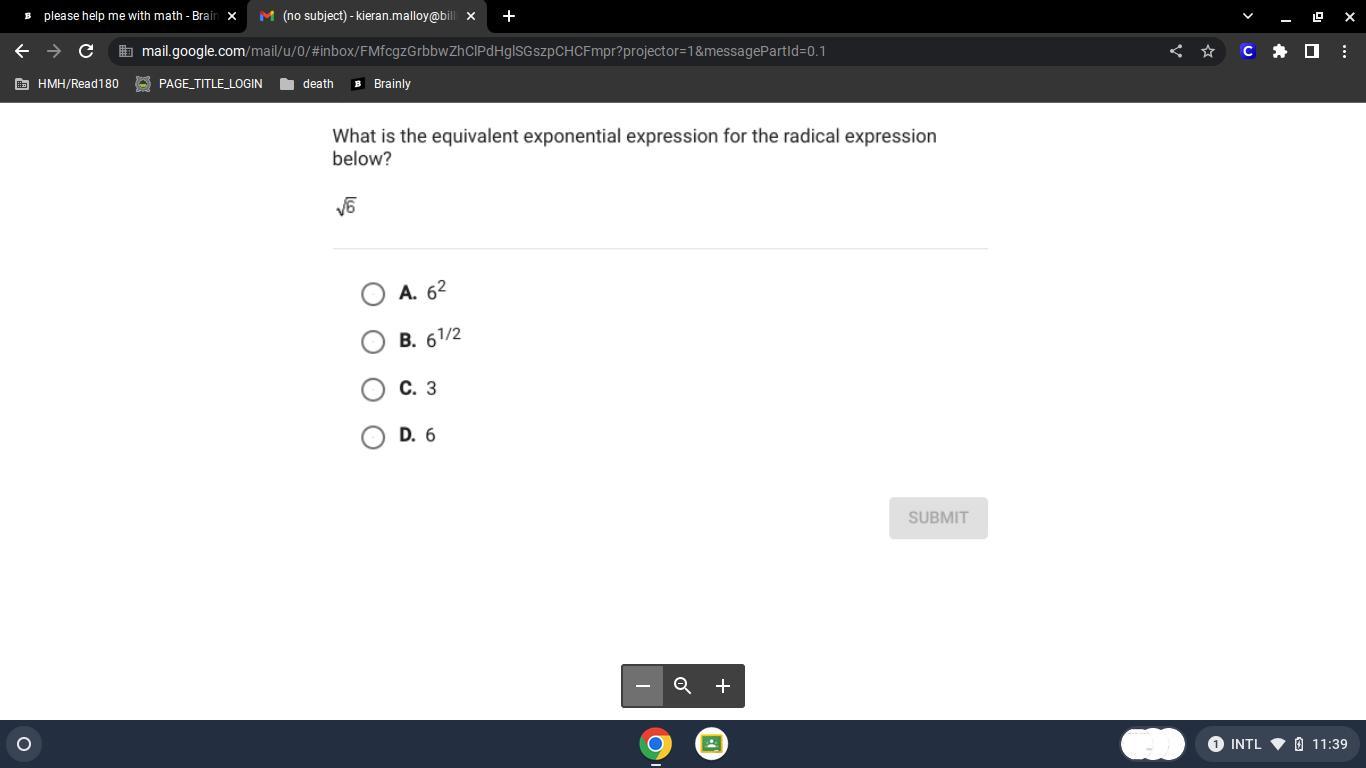
Answers
Answer:
B.) \(6^{\frac{1}{2}}\)
Step-by-step explanation:
Use the exponent rule that states \(a^{\frac{1}{m}}=\sqrt[m]{a}\). For this problem, let
a=6
m=2
So,
\(\sqrt6=6^{\frac{1}{2}}\)
Find the area of the parallelogram 60ft, 26ft, 20ftA.600ftB.1,500ftC.520 ftD. 1,200ft

Answers
Answer:
1,200 ft^2
Explanation:
The area of a parallelogram with height h and base length b is given by
\(Area=bh\)Now, in our case b = 60 ft and h = 20 ft; therefore,
\(\text{Area}=60ft\cdot20ft\)\(\boxed{\text{Area}=1200ft^2}\)which is our answer!
Solve the problems involving slope.
1. Based on the graph, what is the slope
of the line?
y = 2x - 3
Answers
“M” means slope
When you see a number in front of “x” that’s the slope in that case.
16. a bacteria culture starts with 10 00 bacteria and the number doubles every 40minutes.(a) find a formula for the number of bacteria at time t
Answers
The formula that can be used to find the number of bacteria is FV = 1000 x 2^t.
What is the formula that can be used to find the number of bacteria?The formula that can be used to determine the number of bacteria is an exponential function with the form:
FV = P(1 + r)^t
Where:
FV = future population P = present population r - rate of increase1000 x ( 1 + 1)^t
FV = 1000 x 2^t
To learn more about exponential functions, please check: https://brainly.com/question/26331578
#SPJ1
Solve Quadratic Equations by Factoring: Solve by factoring and using the Zero Product Property: 1. X^2-25=0 2. X^2=1=0 3. X^2=x+20 WILL MARK BRAINLIEST!!
Answers
Answer:
1. \(x = \pm 5\)
2. \(x = \pm i\)
3. \(x = 5, -4\)
Step-by-step explanation:
1.
\(x^2-25=0\)
\(x^2 = 25\)
\(x = \pm \sqrt{25}\)
\(x = \pm 5\)
2.
\(x^2 + 1 = 0\)
\(x^2 = -1\)
\(x = \pm \sqrt{x-1}\)
\(x = \pm i\)
3.
\(x^2=x+20\)
\(x^2 - x - 20 = 0\)
\((x-5)(x+4)=0\)
\(x = 5, -4\)
The depth of water in a cylindrical cup of radius r cm is 36cm. the water is then transferred into another cylindrical cup of radius 2r cm. find the depth of the water in the second cup
Answers
The depth of water in the second cup is 9 cm when the water is transferred from a cylindrical cup with a radius of r cm and a depth of 36 cm.
Given that,
Depth of water in the first cylindrical cup with radius r: 36 cm
Transfer of water from the first cup to another cylindrical cup
Radius of the second cup: 2r cm
The first cup has a radius of r cm and a depth of 36 cm.
The volume of a cylinder is given by the formula:
V = π r² h,
Where V is the volume,
r is the radius,
h is the height (or depth) of the cylinder.
So, for the first cup, we have:
V₁ = π r² 36.
Now, calculate the volume of the second cup.
The second cup has a radius of 2r cm.
Call the depth or height of the water in the second cup h₂.
The volume of the second cup is V₂ = π (2r)² h₂.
Since the water from the first cup is transferred to the second cup, the volumes of the two cups should be equal.
Therefore, V₁ = V₂.
Replacing the values, we have
π r² 36 = π (2r)² h₂.
Simplifying this equation, we get
36 = 4h₂.
Dividing both sides by 4, we find h₂ = 9.
Therefore, the depth of the water in the second cup is 9 cm.
To learn more about cylinder visit:
https://brainly.com/question/27803865
#SPJ12
a coin is tossed and a die is rolled. find the probability of getting a head and a number greater than 5
Answers
The probability of getting a head and a number greater than 5 i.e, independent events is 0.0833.
A coin is tossed and a die is rolled. These are two independent events. Two events are defined as independent if the outcome of one event has no effect on the outcome of another event. The probability is calculated by multiplying two independent probabilities together, i.e, P(A and B) = P(A) x P(B)
We have, Let us assume two independent events be ,
A : A coin is tossed and the head is thrown.
B : A die is rolled, and a number greater than 5 occurs.
Total possible outcomes when a coin tossed = 2 ={ H ,T }
Total possible outcomes when a die rolled = 6 = { 1,2,3,4,5,6} .
We have to determine probability of getting a head and a number greater
than 5.
Probability of getting the head on toss a coin, P(A) = 1/2
Probability of occuring a number greater than 5 on rolling a die = P(B) = 1/6
So, the probability of getting a head on coin and a number greater than 5 on die =P(A)×P(B)
=(1/2)× 1/6 = 1/12=0.0833
Hence, required probability is 0.0833.
To learn more about probability, visit:
https://brainly.com/question/13604758
#SPJ4
six boys stood equally spaced on a circle of radius $40$ feet. each boy walked to all of the other non-adjacent persons on the circle, shook their hands and then returned to his original spot on the circle before the next boy started his trip to shake hands with all of the other non-adjacent boys on the circle. after all six boys had done this, what is the least distance in feet that could have been traveled? express your answer in simplest radical form.
Answers
The least distance traveled is \($240\sqrt{3}$\) feet.
Each boy shakes hands with the two boys who are not adjacent to him on the circle. Since there are six boys in total, each boy shakes hands with four other boys. We can represent these handshakes on a graph, where the six vertices represent the six boys and the edges represent the handshakes. Each vertex has degree 4, meaning that there are 12 edges in total.
To minimize the distance traveled, each boy should simply walk directly across the circle to shake hands with the two boys on the opposite side. This way, each boy walks a distance equal to the diameter of the circle, which is \(2 \times 40 = 80$ feet.\)
Since there are six boys, the total distance traveled is \(6 \times 80 = 480$ feet\). However, we have counted each handshake twice, so we need to divide by 2 to get the total distance traveled. This gives us \(240$ feet.\)
To express this answer in the simplest radical form, we can use the fact that an equilateral triangle with side length \(s$\) has height \(s\sqrt{3}/2$\). The six handshakes form an equilateral triangle with side length 80, so its height is \(80\sqrt{3}/2 = 40\sqrt{3}$ feet\). Therefore, the total distance traveled is \(240\sqrt{3}$\) feet.
Therefore, the correct answer is \(240\sqrt{3}$\)feet.
To know more about distance, refer here:
https://brainly.com/question/26711747#
#SPJ11
please help, and please show work if you can <33
Answers
Answer:
where is the question ?
Step-by-step explanation:
Can you help me pls and thank you

Answers
Answer:
80%
Step-by-step explanation:
If you do 4 divided by 5 it equals 0.8, which is 80%
Answer:
The answer is 80%
Step-by-step explanation:
HELP IM STUCK ON THIS QUESTION

Answers
Answer:
FOR THE AREA:
Count how many full squares are in the middle, then count how many halves there are on the outer edge. the divide the amount of halves by 2 then add to the amount of full squares.
This figure has two intersecting lines and a ray. What is the value of x?
108°
72°
19°
37°

Answers
Answer: The answer is 37
Step-by-step explanation:
If you subtract 71 from 108 the answer is 37
Since the angles of (x + 71)º is opposite to the same vertex to the angle of 108º, it is found that x = 37º.
The ray generated two angles, xº and 71º.Adding these angles, there is an angle of (x + 71)º, which is opposite to the same vertex to the angle of 108º, meaning that they have the same measure.
Applying the equality:
\(x + 71 = 108\)
\(x = 108 - 71\)
\(x = 37\)
Thus, x = 37º.
A similar problem is given at https://brainly.com/question/16742265
A perfect square has length n if its last n digits (in base 10) are the same and non-zero. What is the longest possible length? What is the smallest square achieving this length?
Answers
The longest possible length is 3
The smallest square achieving this length : 38² = 1444.
Square:
A quadrilateral with four equal sides is called a square. There are numerous items in our environment that have a square shape. Equal sides and internal angles that are both 90 degrees distinguish each square shape. The complete length of a square's boundary is its perimeter. As a result, the length of each side can be added to determine the square's perimeter. Since a square has four sides, its perimeter may be calculated by adding all four of its sides. The space a square takes up is its area.
To learn more about square visit: https://brainly.com/question/28776767
#SPJ4
James is collecting signatures for a petition. He currently has 520 signatures. He has 6 more weeks to collect the remaining signatures. He needs a total of at least 1,000 signatures before he can submit the petition. James would like to collect the same number of signatures each week.
Answers
Answer:
80 per week
Step-by-step explanation:
1000-520= 480
480/6=80
. If gcd(a, b)-p, a prime, what are the possible values of gcd(a2, b2), gcd(a2, b), and gcd(a3, 2)?
Answers
The possible values are -
(a²,b²) = p
(a²,b) = p if p|-r and (a²,b) = p² if p|r
(a²,b³) = p² if p|-r and (a²,b³) = p³ if p|r
What is gcd?
The greatest common factor (GCF) that divides two or more numbers is known as the greatest common divisor (GCD). The highest common factor is another name for it (HCF).
Since (a, b) = p it can be written a = pr and b = ps where r and s are integers such that (r, s) = 1.
Then a² = p²r².
Then by Theorem 1.7, (a²,b) = (p²r²,ps) = p(pr²,s).
By Theorem 1.8, (r²,s) = 1 .
Thus, there are two cases to consider: if p|s then, (a²,b) = p², and if p|-s then (pr²,s) = 1 (Again by Theorem 1.8) so that (a²,b) = p in that case.
Thus, there are two cases for (a²,b): namely p or p².
The same analysis shows that (a³,b) must be either p, p² or p³ depending on the power of p that divides b.
Analyze (a²,b³) as follows.
Using the notation already introduced, and
Theorem 1.7, it is obtained that (a²,b³) = (p²r²,p³s³) = p²(r²,ps³).
Since, (r, s) = 1, Theorem 1.8 shows that (r²,s³) = 1.
Therefore, there are two possibilities for (a²,b³) -
(a²,b³) = p² if p|-r and (a²,b³) = p³ if p|r.
To learn more about gcd from the given link
https://brainly.com/question/16969353
#SPJ1
Find the signed area between the graph of y=x²-4 and the z-axis, over the interval [1, 3]. Area =
Answers
The signed area between the graph of y=x²-4 and the z-axis, over the interval [1, 3], is 8 square units.
To find the signed area between the graph of y=x²-4 and the z-axis over the interval [1, 3], we can use the concept of definite integration. The signed area represents the area above the x-axis minus the area below the x-axis.
First, we need to determine the points of intersection between the graph y=x²-4 and the x-axis. Setting y equal to zero, we have:
0 = x² - 4
Solving this equation, we find x = ±2. So, the graph intersects the x-axis at x = -2 and x = 2.
Next, we integrate the function y=x²-4 over the interval [1, 3]. This can be done by finding the definite integral of the function:
∫[1, 3] (x² - 4) dx
Evaluating this integral, we get:
[1/3 * x³ - 4x] [1, 3]
= (1/3 * 3³ - 4*3) - (1/3 * 1³ - 4*1)
= (1/3 * 27 - 12) - (1/3 * 1 - 4)
= (9 - 12) - (1/3 - 4)
= -3 - (-11/3)
= -3 + 11/3
= 8/3
The signed area between the graph y=x²-4 and the z-axis, over the interval [1, 3], is 8/3 square units.
Learn more about signed area
brainly.com/question/30662668
#SPJ11
PLEASEEEEE HELP! Drag the numbers to the correct locations in the equation. Each number can be used more than once, but not all numbers will be used. The average commute time, in minutes, in relation to the population, in millions, of 10 major cities is shown in the table. What is the square root equation that best models this set of data?

Answers
9514 1404 393
Answer:
\(y=10.9\sqrt{x-0.5}+23.7\)
Step-by-step explanation:
A graphing calculator or spreadsheet can help you do the square root regression. See the attachment for the result.
\(y=10.9\sqrt{x-0.5}+23.7\)

Answer:
see image
Step-by-step explanation:
Plato/Edmentum

Slide the green dot from 0 to plot the number at the correct
location.
Use the interactive to solve the following problems:
Plot -12
What is the difference between -12 and 5?
-14
-12
-10
-8
-6
-4
-2
0
What is the distance between -12 and 7 on a number
line?
units
Answers
Answer:
-8
tama po yan ng solve po ako Dyan
ikaw nalang po mag mag number line
Answer:
-7 and 5
Step-by-step explanation:
hope it helped ya
Draw a diagram to show that (2x+5)(x+3) is equivalent to 2x^2 + 11x + 15?

Answers
Answer:
Use a punnet square type of diagram
Step-by-step explanation:

What is the y-value of the solution to the system of equations? 3x 5y = 1 7x 4y = −13
Answers
The solution to the system of equations is x = -3 and y = 2. The y-value of the solution is 2
To find the y-value of the solution to the system of equations, we can solve the system using any suitable method such as substitution or elimination.
Given system of equations:
3x + 5y = 1
7x + 4y = -13
Let's use the method of elimination to solve the system:
Multiply equation 1 by 4 and equation 2 by 5 to make the coefficients of y in both equations equal:
4(3x + 5y) = 4(1) --> 12x + 20y = 4
5(7x + 4y) = 5(-13) --> 35x + 20y = -65
Now, subtract equation 1 from equation 2 to eliminate the y term:
(35x + 20y) - (12x + 20y) = -65 - 4
35x - 12x = -69
23x = -69
x = -69/23
x = -3
Substitute the value of x into equation 1 to find y:
3(-3) + 5y = 1
-9 + 5y = 1
5y = 1 + 9
5y = 10
y = 10/5
y = 2
Therefore, the solution to the system of equations is x = -3 and y = 2. The y-value of the solution is 2.
For more details of equations :
https://brainly.com/question/21620502
#SPJ4
(-3) - (+4) - (+2) - (-1)
Answers
Answer:
-8
Step-by-step explanation:
-3-4-2+1
-8
Surface area of image

Answers
The surface area of the cuboid is 3.286 cm²
What are the surface area of a cuboid?A cuboid is a solid shape or a three-dimensional shape.
Surface area is the amount of space covering the outside of a three-dimensional shape.
The surface area of a cuboid is expressed as;
SA = 2( lb + lh + bh)
length = 1 2/5 = 7/5
breadth = 5/8
height = 3/8
lb = 7/5 × 5/8 = 7/8
bh = 5/8 × 3/8 = 15/64
lh = 7/5 × 3/8 = 21/40
surface area =2( 7/8 + 15/64+21/40)
= 2( 0.875 + 0.234 + 0.525)
= 2( 1.634)
= 3.268 cm²
The surface area of the cuboid is 3.268 cm²
learn more about surface area of cuboid from
https://brainly.com/question/26403859
#SPJ1
HeLp mE sO I cAn GeT A gOoD GrAdE

Answers
Answer:
It is C
Step-by-step explanation:
7/2 is 3.5. We can see that if we multiply the y value of 2 for d, it becomes 7, which is shown there. All other choices do not make sense.
a room contains several urns. 13 urns contain two gold balls. 6 urns contain one gold ball and one silver ball. 20 urns contain two silver balls. you choose an urn at random and then draw two balls from the urn. if the first ball you draw is gold, what is the probability that the second ball you draw is gold?
Answers
The probability that the second ball you draw is gold is 0.619.
What is the probability?
A probability is a number that reflects the chance or likelihood that a particular event will occur. Probabilities can be expressed as proportions that range from 0 to 1, and they can also be expressed as percentages ranging from 0% to 100%.
Here, we have
Given: a room contains several urns 13 urns contain two gold balls, 6 urns contain one gold ball and one silver ball, 20 urns contain two silver balls.
Conditional probability is a measure of the probability of an event occurring given that another event has occurred.
Here given event is that first ball is gold. Hence sample space will have 13+8 = 21 urns.
For second ball to be gold, urn should have 2 gold balls hence it has 13 urns under above condition.
Probability = 13/21 = 0.619
Hence, the probability that the second ball you draw is gold is 0.619.
To learn more about the probability from the given link
https://brainly.com/question/7965468
#SPJ4
let φ(u,v)=(3u 3v,8u 6v). use the jacobian to determine the area of φ(r) for:
Answers
The area of the image φ(r) can be determined using the Jacobian of the transformation φ(u, v). The area of φ(r) is zero
The Jacobian matrix for φ(u, v) is given by:
J(u, v) = [[∂(3u)/∂u, ∂(3u)/∂v], [∂(8u)/∂u, ∂(8u)/∂v]] = [[3, 0], [8, 0]]
The Jacobian determinant is calculated as the determinant of the Jacobian matrix:
|J(u, v)| = |[[3, 0], [8, 0]]| = 3 * 0 - 0 * 8 = 0
Since the Jacobian determinant is zero, it indicates that the transformation φ(u, v) degenerates into a line or a point. This means that the image of φ(r) has zero area, as it collapses onto a lower-dimensional object. In other words, the transformation does not preserve the area of the region r.
Hence, the area of φ(r) is zero, implying that the transformation φ(u, v) in this case causes a loss of dimensionality, resulting in a line or point rather than a region with non-zero area.
Learn more about transformation here:
https://brainly.com/question/11709244
#SPJ11