Find the distance between the points ( 1, 4 ) and ( -2, -1 )
Answers
4- (-1)= 5
3/5 is the slope to find the distance
Related Questions
3. The carrying capacity of a drain pipe is directly proportional to the area of its cross- section. If a cylindrical drain pipe can carry 36 litres per second, determine the percentage increase in the diameter of the drain pipe necessary to enable it to carry 60 litres per second.
Answers
The percentage increase in the diameter of the drain pipe necessary to enable it to carry 60 litres per second is 28.87%.
Given that the carrying capacity is directly proportional to the area, we can write:
C1 ∝ A1 = πr₁²
Since the carrying capacity is directly proportional to the area, we have:
C2 ∝ A2 = πr₂²
To find the percentage increase in diameter, we need to find the ratio of the increased area to the initial area and then express it as a percentage. Let's calculate this ratio:
(A2 - A1) / A1 = (πr₂² - πr₁²) / (πr₁²) = (r₂² - r₁²) / r₁²
We can also express the ratio of the increased carrying capacity to the initial carrying capacity:
(C2 - C1) / C1 = (60 - 36) / 36 = 24 / 36 = 2 / 3
Since the area and the carrying capacity are directly proportional, the ratios should be equal:
(r₂² - r₁²) / r₁² = 2 / 3
Now, let's substitute r = D/2 in the equation:
((D₂/2)² - (D₁/2)²) / (D₁/2)² = 2 / 3
(D₂² - D₁²) / D₁² = 2 / 3
Cross-multiplying:
3(D₂² - D₁²) = 2D₁²
3D₂² - 3D₁² = 2D₁²
3D₂² = 5D₁²
Dividing by D₁²:
3(D₂² / D₁²) = 5
(D₂² / D₁²) = 5 / 3
Taking the square root of both sides:
D₂ / D₁ = √(5/3)
To find the percentage increase in diameter, we subtract 1 from the ratio and express it as a percentage:
Percentage increase = (D₂ / D₁ - 1) × 100
Percentage increase = (√(5/3) - 1) × 100
Percentage increase = 28.87%
To learn more on Percentage click:
https://brainly.com/question/24159063
#SPJ1
A normal distribution curve, where x = 70 and o = 15,
was created by a teacher using her students' grades.
What information about their performances can be obtained by analyzing the curve?
Answers
The normal distribution curve gives useful information regarding the distribution of students' grades, such as the average grade, the dispersion of grades, the likelihood of receiving a specific grade, and the presence of any outliers.
Obtainable Information's from the Distribution Curve?The normal distribution curve generated by the educator offers multiple insights into the distribution of academic achievement among her pupils. The analysis of the curve yields various informative data such as:
The parameter of central tendency for this distribution is represented by the mean, denoted as x=70, signifying that the students' mean grade is at 70.The normal distribution's degree of dispersion is represented by the standard deviation, denoted by o=15 in this context, conveying the extent of variability among grades. In this particular instance, the presence of a higher standard deviation denotes a greater degree of variability in the distribution of grades from the central tendency.Probability theory allows for the utilization of the normal distribution curve to determine the likelihood of a student achieving a particular grade. An illustration of this notion can be depicted by estimating the likelihood of an individual receiving a marks within the range of 55 and 85 through the computation of the region beneath the curve that occupies those particular values.The utilization of the normal distribution in statistical analysis is instrumental in recognizing any possible outliers within the dataset. An outlier refers to a data point that deviates considerably from the rest of the data. In the present scenario, grades whose values extend beyond two standard deviations from the mean, calculated as 70 + 215 = 100 or 70 - 215 = 40, may be considered as outliers.Learn more about distribution curve here: https://brainly.com/question/23418254
#SPJ1
Line g is dilated by a scale factor of 1/2 from the origin to create line g'. Where are points E' and F' located after dilation, and how are lines g and g' related? 4 3 g 1 E -5 -2 -1 0 -1 -2

Answers
C) The lines g and g' are parallel and E'(-2,0) and F'(0, 1)
1) Let's locate points E and F.
E (0,2) and F( -4,0)
Given that line was dilated by a scale factor k = 1/2 about the origin we can state the following
• The line segment g' is shorter, half of g.
,• Points E'(0,1) and F'(0,1)
3) Examining the answers we can state:
The lines g and g' are parallel and E'(-2,0) and F'(0, 1)
57\% of all us households have someone available to answer unsolicited calls. assuming that households answer (or not) independently of one another, what is the probability that calls to exactly two randomly selected households will both go unanswered?
Answers
The probability that calls to exactly two randomly selected households will both go unanswered is 0.1849
Calculating the probability that both calls will go unanswered?
From the question, we have the following parameters that can be used in our computation:
Probabiity of answering, p = 57%
This means that the probability that no one answers the call is
q = 1 - 57%
Evaluate
q = 43%
So, the probability that both calls will go unanswered is
P = q²
This gives
P = (43%)²
Evaluate
P = 0.1849
Hence, the probability is 0.1849
Read more about probability at
https://brainly.com/question/251701
#SPJ1
what is dx in calculus
Answers
In calculus, dx is a symbol used to represent a small change or increment in the variable x.
It is commonly used in derivative and integral expressions to indicate the variable of differentiation or integration.
For example, if we have the function f(x) and want to find its derivative, we would write it as df/dx, which represents the change in f with respect to the change in x.
Similarly, if we want to find the integral of a function g(x), we would write it as ∫g(x)dx, which represents the sum of all the small changes in g(x) multiplied by the corresponding small changes in x.
In short, dx is used to indicate the variable of differentiation or integration in calculus.
To know more about calculus refer here:
https://brainly.com/question/6581270#
#SPJ11
A two-digit number is such that the sum of its digits is 11. When the digits of the number are reversed and the number is subtracted from the original number, the result obtained is 9 Find the original number.
Answers
By writing and solving a system of equations we will find that the number is 56
So we can write a two-digit number as:
a*10 + b
Where the two digits are a and b.
Here we must have:
a + b = 11
The reversed number is:
b*10 + a
Then we can write the equation:
b*10 + a - a*10 - b = 9
b*9 - a*9 = 9
Then we have a system of two equations:
a + b = 11
b*9 - a*9 = 9
We can divide both sides of the second equation by 9 to get:
b - a = 1
Now we can isolate b to get:
b = 1 + a
Now we can replace this in the other equation.
a + b = a + (1 + a) = 11
2a + 1 = 11
2a = 11 - 1 = 10
a = 10/2 = 5
Now we have the value of a, and we know that:
b = 1 + a = 1 + 5 = 6
Then the two-digit number is:
a*10 + b = 5*10 + 6 = 56
If you want to learn more about systems of equations, you can read:
https://brainly.com/question/13729904
Jamal is x years old. His mother is 28 years older than Jamal. Jamal's uncle is two times older than Jamal's mother. Write and simplify an expression that represents Jamal's uncle age in years
Answers
Given: Jamal is x years old.
⠀⠀⠀⠀━━━━━━━━━━━━━━━━━━
And, his mother is 28 years older than Jamal.
Then, age of Jamal's mother is = (x + 28)
⠀⠀⠀
Jamal's uncle is two times older than Jamal's mother.⠀⠀⠀
\(:\implies\sf Jamal's\: uncle\:age = (Jamal's mother age)\\\\\\ :\implies\sf Jamal's\: uncle\:age = 2(x + 28)\\\\\\ :\implies{\underline{\boxed{\pmb{\frak{\purple{Jamal's\: uncle\:age = 2x + 56}}}}}}\:\bigstar\\\\\)
\(\therefore\:{\underline{\sf{Hence,\:the\:expression\:that\: represents\: Jamal's\: uncle \:age\:is\: {\pmb{2x + 36}}.}}}\)
est the series for convergence or divergence using the alternating series test. [infinity] (−1)n 2nn n! n = 1
Answers
The Alternating Series Test (AST) is used to determine if a series is convergent or divergent. It assumes that the terms alternate in sign and are monotonically decreasing in magnitude, and if lim_(n)a_n = 0, then the series is convergent. The series is given in the general formula for the AST, and the absolute value of each term is equal to the corresponding term.
The series for convergence or divergence using the alternating series test is given below:
[infinity] (−1)n 2nn n! n = 1
The general formula for the alternating series test is as follows. Assume that a series [a_n]_(n=1)^(∞) is defined such that the terms alternate in sign and are monotonically decreasing in magnitude.
If lim_(n→∞)△a_n = 0, where △a_n denotes the nth term of the series,
then the alternating series [a_n]_(n=1)^(∞) is convergent. We must evaluate if the alternating series is monotonically decreasing and if the absolute value of each term of the series is decreasing as well. If both conditions are met, we may apply the Alternating Series Test (AST). Let's take a look at the given series below:(-1)^n(2^n)/(n!) for n = 1 to infinity The series is given in the general formula for the AST. Because the series is already in the right form, we do not need to test it first.
The terms of the sequence decrease since (n+1)!/(n!) = (n+1), which is a positive number. Furthermore, since (n+1) > n for any natural number n, the sequence decreases monotonically. When we take the absolute value of each term in the series, it is equal to the corresponding term since all terms are positive.
Therefore, the series is convergent according to the Alternating Series Test.
To know more about Alternating Series Test Visit:
https://brainly.com/question/30400869
#SPJ11
reduce these to the simplest terms

Answers
Answer:
16. 1/2
17. 3/4
18. 1/3
19. 1/4
20. 2/3
21. 1/7
22. 1/4
23. 1/7
Answer:
16. 1/2 or 1 over 2
17. 3/4 or 3 over 4
18. 1/3 or 1 over 3
19. 1/4 of 1 over 4
20. 2/3 or 2 over 3
21. 1/7 or 1 over 7
22. 1/4 or 1 over 4
23. 1/7 or 1 over 7
Please Brainliest would be much appreciated
a cereal box is 10.4 inches high 7.4 inches long and 2.3 inches wide. what is the volume of the cereal box rounded to the nearest cubic inch
Answers
Answer:
177.008in^3
Step-by-step explanation:
Given data
Height= 10.4in
Lenght= 7.4in
Width= 2.3in
The expression for the volume of a box is given as
Volume= Length*width*Height
Volume= 10.4*7.4*2.3
Volume= 177.008 in^3
Hence the volume is 177.008in^3
patricia's parents buy her too much stuff, so she had 3 times as many as her friend suzy. if patricia has 15 toy trucks, how many does suzy have?
Answers
The solution of units problem is Suzy has 5 toy trucks by using the equation 15 = 3 * Suzy's number of toy trucks
According to the given information:
If Patricia has 3 times as many toy trucks as Suzy, we can set up an equation where:
Patricia's number of toy trucks = 3 * Suzy's number of toy trucks
We know that Patricia has 15 toy trucks, so we can substitute that value into the equation:
15 = 3 * Suzy's number of toy trucks
Now we can solve for Suzy's number of toy trucks:
Suzy's number of toy trucks = 15 / 3
Suzy's number of toy trucks = 5
Therefore, Suzy has 5 toy trucks.
To know more about Equation Visit:
https://brainly.com/question/10413253
#SPJ1
What type of variable is required when drawing a time-series plot? Why do we draw time-series plots?
A_____quantitative variable is required when drawing a time-series plot.
Select all the reasons why time-series plots are used.
A. Time-series plots are used to examine the shape of the distribution of the data.
B. Time-series plots are used to identify any outliers in the data.
C. Time-series plots are used to identify trends in the data over time.
D. Time-series plots are used to present the relative frequency of the data in each interval or category.
Answers
Time-series plots are used for several reasons:
B. Time-series plots are used to identify any outliers in the data.
C. Time-series plots are used to identify trends in the data over time.
D. Time-series plots are used to present the relative frequency of the data in each interval or category.
How to determine the plotFirst, we need to know that quantitative variable is required when drawing a time-series plot.
We need to also know that data points are graphically represented as time-series plots, with the variable of interest drawn on the y-axis and time commonly depicted on the x-axis. They demonstrate the variable's evolution over time.
Learn more about time-series plots at: https://brainly.com/question/29654037
#SPJ1
The line parallel to y=3x+5 that passes through the point (-8,-4)
Answers
Answer:
y = 3x + 20
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = 3x + 5 ← is in slope- intercept form
with slope m = 3
• Parallel lines have equal slopes , then
y = 3x + c ← is the partial equation
to find c substitute (- 8, - 4 ) into the partial equation
- 4 = - 24 + c ⇒ c = - 4 + 24 = 20
y = 3x + 20 ← equation of parallel line
Answer:
Step-by-step explanation: From the given point,
The line is: -8x-4y=0
viz, 2x+y=0
Will choose brain list

Answers
Answer:
Real, Rational
Step-by-step explanation:
The Set of integers includes zero, positive and negative numbers (not fractions)
Whole numbers include only zero and positive numbers.
Irrational numbers can't be expressed as a fraction; in fact, it's an infinite decimal.
So 0/3 is real and rational. Hope it helps!
10 times much as 5000
Answers
Answer:
50,000
Step-by-step explanation:
10*5,000=50,000
Answer: 50,000
Step-by-step explanation:
10× 5,000= 50,000
Or
Just add one zero to 5,000 :)
Hope this helps :)
The Center for Disease Control and Prevention reports that 25% of bay boys 6-8 months old in the United States weigh more than 20 pounds. A sample of 16 babies is studied.
Answers
Okay, it seems like you want to analyze a sample of 16 babies based on their weight.
The information you provided states that the Center for Disease Control and Prevention reports that 25% of baby boys aged 6-8 months in the United States weigh more than 20 pounds.
However, you haven't mentioned the specific question or analysis you want to perform on the sample. Could you please clarify what you would like to know or do with the given information?
To know more about Prevention visit-
brainly.com/question/30892272
#SPJ11
Please answer this question, i request
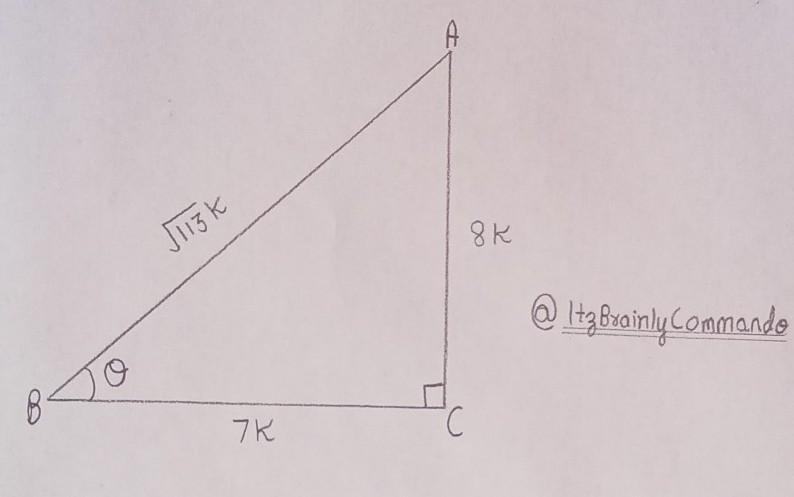
If cot θ = 7/8 , evaluate :-
(1 + sin θ)(1 – sin θ)/(1 + cos θ)(1 - cos θ)
Answers
\({\large{\textsf{\textbf{\underline{\underline{Given :}}}}}}\)
\( \star \: \tt \cot \theta = \dfrac{7}{8} \)
\( {\large{\textsf{\textbf{\underline{\underline{To \: Evaluate :}}}}}}\)
\( \star \: \tt \dfrac{(1 + \sin \theta)(1 - \sin \theta) }{(1 + \cos \theta) (1 - \cos \theta) }\)
\({\large{\textsf{\textbf{\underline{\underline{Solution :}}}}}}\)
Consider a \(\triangle\) ABC right angled at C and \(\sf \angle \: B = \theta \)
Then,
‣ Base [B] = BC
‣ Perpendicular [P] = AC
‣ Hypotenuse [H] = AB
\( \therefore \tt \cot \theta = \dfrac{Base}{ Perpendicular} = \dfrac{BC}{AC} = \dfrac{7}{8}\)
Let,
Base = 7k and Perpendicular = 8k, where k is any positive integer
In \(\triangle\) ABC, H² = B² + P² by Pythagoras theorem
\( \longrightarrow \tt {AB}^{2} = {BC}^{2} + {AC}^{2} \)
\( \longrightarrow \tt {AB}^{2} = {(7k)}^{2} + {(8k)}^{2} \)
\(\longrightarrow \tt {AB}^{2} = 49{k}^{2} + 64{k}^{2} \)
\(\longrightarrow \tt {AB}^{2} = 113{k}^{2} \)
\(\longrightarrow \tt AB = \sqrt{113 {k}^{2} } \)
\(\longrightarrow \tt AB = \red{ \sqrt{113} \: k}\)
Calculating Sin \(\sf \theta \)
\( \longrightarrow \tt \sin \theta = \dfrac{Perpendicular}{Hypotenuse}\)
\( \longrightarrow \tt \sin \theta = \dfrac{AC}{AB}\)
\(\longrightarrow \tt \sin \theta = \dfrac{8 \cancel{k}}{ \sqrt{113} \: \cancel{ k } }\)
\(\longrightarrow \tt \sin \theta = \purple{ \dfrac{8}{ \sqrt{113} } }\)
Calculating Cos \(\sf \theta \)
\( \longrightarrow \tt \cos \theta = \dfrac{Base}{Hypotenuse}\)
\( \longrightarrow \tt \cos \theta = \dfrac{BC}{ AB} \)
\( \longrightarrow \tt \cos \theta = \dfrac{7 \cancel{k}}{ \sqrt{113} \: \cancel{k } }\)
\(\longrightarrow \tt \cos \theta = \purple{ \dfrac{7}{ \sqrt{113} } }\)
Solving the given expression :-
\( \longrightarrow \: \tt \dfrac{(1 + \sin \theta)(1 - \sin \theta) }{(1 + \cos \theta) (1 - \cos \theta) } \)
Putting,
• Sin \(\sf \theta \) = \(\dfrac{8}{ \sqrt{113} }\)
• Cos \(\sf \theta \) = \(\dfrac{7}{ \sqrt{113} }\)
\( \longrightarrow \: \tt \dfrac{ \bigg(1 + \dfrac{8}{ \sqrt{133}} \bigg) \bigg(1 - \dfrac{8}{ \sqrt{133}} \bigg) }{\bigg(1 + \dfrac{7}{ \sqrt{133}} \bigg) \bigg(1 - \dfrac{7}{ \sqrt{133}} \bigg)} \)
Using (a + b ) (a - b ) = a² - b²
\(\longrightarrow \: \tt \dfrac{ { \bigg(1 \bigg)}^{2} - { \bigg( \dfrac{8}{ \sqrt{133} } \bigg)}^{2} }{ { \bigg(1 \bigg)}^{2} - { \bigg( \dfrac{7}{ \sqrt{133} } \bigg)}^{2} } \)
\(\longrightarrow \: \tt \dfrac{1 - \dfrac{64}{113} }{ 1 - \dfrac{49}{113} } \)
\(\longrightarrow \: \tt \dfrac{ \dfrac{113 - 64}{113} }{ \dfrac{113 - 49}{113} } \)
\(\longrightarrow \: \tt { \dfrac { \dfrac{49}{113} }{ \dfrac{64}{113} } }\)
\(\longrightarrow \: \tt { \dfrac{49}{113} }÷{ \dfrac{64}{113} }\)
\(\longrightarrow \: \tt \dfrac{49}{ \cancel{113}} \times \dfrac{ \cancel{113}}{64} \)
\(\longrightarrow \: \tt \dfrac{49}{64} \)
\(\qquad \: \therefore \: \tt \dfrac{(1 + \sin \theta)(1 - \sin \theta) }{(1 + \cos \theta) (1 - \cos \theta) } = \pink{\dfrac{49}{64} }\)
\(\begin{gathered} {\underline{\rule{300pt}{4pt}}} \end{gathered} \)
\( {\large{\textsf{\textbf{\underline{\underline{We \: know :}}}}}}\)
✧ Basic Formulas of Trigonometry is given by :-
\(\begin{gathered}\begin{gathered}\boxed { \begin{array}{c c} \\ \bigstar \: \sf{ In \:a \:Right \:Angled \: Triangle :} \\ \\ \sf {\star Sin \theta = \dfrac{Perpendicular}{Hypotenuse}} \\\\ \sf{ \star \cos \theta = \dfrac{ Base }{Hypotenuse}}\\\\ \sf{\star \tan \theta = \dfrac{Perpendicular}{Base}}\\\\ \sf{\star \cosec \theta = \dfrac{Hypotenuse}{Perpendicular}} \\\\ \sf{\star \sec \theta = \dfrac{Hypotenuse}{Base}}\\\\ \sf{\star \cot \theta = \dfrac{Base}{Perpendicular}} \end{array}}\\\end{gathered} \end{gathered}\)
\({\large{\textsf{\textbf{\underline{\underline{Note :}}}}}}\)
✧ Figure in attachment
\(\begin{gathered} {\underline{\rule{200pt}{1pt}}} \end{gathered} \)
23. Match the figure with the number of unit cubes that would be needed to build each figure. Not every number of unit cubes will be used.

Answers
We can see here that:
Figure 1 - 7 unit cubes.Figure 2 - 6 unit cubes.What is cube?A cube is a three-dimensional geometric shape that has six square faces, all of which are congruent (equal in size) and perpendicular to each other. It is a special type of rectangular prism where all edges have the same length, and all angles are right angles (90 degrees).
Cubes are commonly encountered in everyday life, such as dice, boxes, and Rubik's Cube puzzles. They have precise and uniform geometry, making them useful in various mathematical and engineering applications.
Learn more about cube on https://brainly.com/question/19891526
#SPJ1
find the product of 7/2 and 22
Answers
Cancel out the GCF 2:
7x11
The answer is 77
Answer:
98765
Step-by-step explanation:
HELPPP MEE PLSSS
Find m∠2

Answers
Answer:
Step-by-step explanation:
180-68=112
1= 68
2=112
For a point to be a solution to a
system of inequalities, the point
must make_ of the
inequalities true.
Answers
Answer:
The signs.Step-by-step explanation:
For a point to be a solution to a system of inequalities, the points must make the signs of the inequalities true.
For example, the points must give results like 2<3 or 0>-2, these are true solutions. If the points gives 1>2, then that point is not a solution.
define decimal in simplest forms
Answers
Answer:
A decimal number is a number that has two parts, the whole and the fractional. These parts are divided by a decimal point. For example: 7.45 or 102.7 are decimal numbers.
Represent the following sentence as an algebraic expression, where "a number" is the letter x. The quotient of 1 and a number. The quotient of 1 and a number.
Answers
Answer:
8+2x=18
x=______
10x+4=44
x=_____
Find sin D, sin E, cos D, and cos E. Write each answer as a fraction in simplest form
Answers
To find the values of sin D, sin E, cos D, and cos E, we need additional information such as the measures of angles D and E or the lengths of the sides of the triangle.
However, based on the information you provided (9, 12, 15), we can make some assumptions.
If we assume that the triangle is a right triangle, with side lengths of 9, 12, and 15, we can use the Pythagorean theorem to find the missing side lengths. The side lengths satisfy the Pythagorean theorem: 9^2 + 12^2 = 15^2.
Using these assumptions, we can calculate the values of sin D, sin E, cos D, and cos E. Since angle D is opposite side 9 and angle E is opposite side 12, we have:
sin D = 9/15 = 3/5
sin E = 12/15 = 4/5
cos D = 12/15 = 4/5
cos E = 9/15 = 3/5
Please note that these values are based on the assumption of a right triangle with side lengths of 9, 12, and 15.
Learn more about triangle here: brainly.com/question/2773823
#SPJ11
Complete question: Find Sin D, Sin E, Cos D, And Cos E. Write Each Answer As A Fraction In Simplest Form. 9 12 15 E Sin D = Sin E= Cos D= Cos E.
a farmer made a loss of 28% by selling a gold for1440shillings what percentage profit would have made if he had sold the goat.for.sh 2100
Answers
The farmer would have made a profit of 5% if he had sold the goat for 2100 shillings.
Let's use the given terms and find out the percentage profit if the farmer had sold the goat for 2100 shillings.
Calculate the cost price of the goat
We know that the farmer made a loss of 28% by selling the goat for 1440 shillings. Let's represent the cost price as "CP".
We can write the equation:
\(CP \times (1 - loss% ) = selling price (SP)\)
\(CP \times (1 - 0.28) = 1440\)
Solve for CP
\(CP \times 0.72 = 1440\)
CP = 1440 / 0.72
CP = 2000 shillings
Calculate the percentage profit
Now we want to find out the percentage profit if the farmer had sold the goat for 2100 shillings.
We can write the equation:
\((SP_{new - CP)} / CP \times 100 = profit\)
\((2100 - 2000) / 2000 \times 100 = profit%\)
\(100 / 2000 \times 100 = profit%\)
5% = profit%.
For similar question on profit.
https://brainly.com/question/29087694
#SPJ11
p is directly proportional to (q+2)2.
When q = 1, p= 1.
Find p when q = 10.
Answers
Answer:
p = 16
Step-by-step explanation:
Given p is directly proportional to (q + 2)² then the equation relating them is
p = k(q + 2)² ← k is the constant of proportion
To find k use the condition when q = 1, p = 1
1 = k(1 + 2)² = k × 3² = 9k ( divide both sides by 9 )
\(\frac{1}{9}\) = k
p = \(\frac{1}{9}\) (q + 2)² ← equation of proportion
When q = 10 , then
p = \(\frac{1}{9}\) × (10 + 2)² = \(\frac{1}{9}\) × 12² = \(\frac{1}{9}\) × 144 = 16
URGENT NEED HELP FAST

Answers
Answer: I think it’s the 4th one
Step-by-step explanation:
Answer:
2nd one
Step-by-step explanation:
Shaded below means less than
How do you solve an equation with x and y in one?
Answers
There are infinitely many solutions to an equation with two variables.
We know that an equation is a mathematical statement that contains equal symbol between two mathematical expressions.
In this question need to solve an equation with x and y in one equation.
Consider an equation with two variables: 5x + y = 8
If we solve given equation for x then it would be,
5x + y = 8
5x + y - y = 8 - y
5x/5 = (8 - y)/5
x = (8 - y)/5
for any arbitrary real value value of y we can find the value of x.
This means there are infinitely many solutions.
If we solve given equation for y then it would be,
5x + y = 8
5x + y - 5x = 8 - 5x
y = 8 - 5x
for any arbitrary real value value of x we can find the value of y.
Therefore, an equation with two variables has infinitely many solutions.
Learn more about an equation here:
https://brainly.com/question/649785
#SPJ4
Which of the following is a solution to the inequality below?

Answers
Answer:
B=3
Step-by-step explanation:
30/3=10
the inequality wanted some thing equal or grater so 30/3=10
Fill in the blanks to complete the proofs

Answers
Answer:
Look at the image I attached to my response.
Step-by-step explanation:
For proof #3, I did it according to the way I was taught how to do proofs in my state/school, so what you wrote could be correct.
