Answers
Answer:
Assuming you are asking for the slope which is 3 or in the equation format y=3x
Step-by-step explanation:
you must find the distance in the y- values and the x values, how each value increases or decreases. You may have heard of the phrase rise/run. To get to the pint (2,6) from (1,3), you must rise 3 units and move 1 unit. If you were to follow the rise/run method, you will need to divide the two numbers. In this case you will be dividing 3/1 which equals you. Then you must plug that number into the formula (y=mx+b).
Related Questions
Help me please!! I need a good grade

Answers
Answer:
The answer of this question is 8.06 cm.
Step-by-step explanation:
I came to know my answer is correct because hypotenuse is bigger than base and perpendicular in right anhled triangle.

The slope of the line below is -1/7. write a point slope equation of the line using the coordinates of the labeled point.

Answers
The equation of a straight line can be written if its slope and any one point lying on it is given. The equation of the line for given slope and point is (y - 3) = -1 / 7 × (x - 3). The correct answer is option B.
What is the equation for a straight line?A straight line can be written in the form of equation as, y = mx + c.
Two straight lines intersect each other only at one point.
When two straight lines are parallel to each other the angle between them is zero.
Given that,
The slope of the line = -1 / 7
The coordinate of the point on the line = (3,3)
The equation of a line having slope m and passing through a point (x₁, y₁) is given as,
(y - y₁) / (x - x₁) = m
Thus, the equation of the line for given slope and point is given as,
(y - 3) / (x - 3) = -1 / 7
=> (y - 3) = -1 / 7 × (x - 3)
Hence, the equation of the line for given slope and point is (y - 3) = -1 / 7 × (x - 3).
To know more about straight line equation click on,
https://brainly.com/question/21627259
#SPJ1
Do the following pairs of equations represent parallel lines,
perpendicular lines, or neither; y = -1/2 x + 5 and y = -1/2 x - 9?
Answers
Answer:
Parallel
Step-by-step explanation:
What makes two lines parallel?For two lines to be parallel, they must have the same slope.
These are linear equations, which are represented by \(y=mx+b\) where m is the slope and b is the y-intercept.
In this pair of equations, we can see that the m (or the slope) are exactly the same (\(-\frac{1}{2} = -\frac{1}{2}\)). This means that they are parallel.
What makes two lines perpendicular?Two lines are perpendicular when the slope of one of them is equal to the negative reciprocal of the other.
For example, to find the perpendicular line to \(y=-\frac{1}{2}x+5\) we would get the m (\(-\frac{1}{2}\)) and find its negative reciprocal.
\(-(-\frac{2}{1}) = 2\)
We can verify this graphically by using a calculator (if you have a graphing calculator) or we can use the Desmos tool (online graphing calculator). Please see the image that's attached to this answer. It's evident that they are perpendicular in this image due to the fact that they make an angle of 90 degrees.
Let me know if there's something you'd like me to explain further. Good luck!

Choose a company with your option and explain how
that company can create a business model? There are 8 steps in the
business module, explain each step based on the company which you
have chosen.
Answers
Company: Amazon, 8 Steps in the Business Model: Define the value proposition. What value does Amazon offer its customers? Amazon offers a convenient and affordable way to shop for a wide variety of products.
Identify the target market. Who are Amazon's customers? Amazon's target market is people who want to buy products online.
Determine the revenue streams. How does Amazon make money? Amazon makes money through product sales, advertising, and subscription fees.
Assess the cost structure. What are Amazon's costs? Amazon's costs include salaries, rent, and marketing.
Develop a marketing plan. How will Amazon reach its target market? Amazon's marketing plan includes online advertising, search engine optimization, and social media marketing.
Create a sales strategy. How will Amazon sell its products? Amazon's sales strategy includes a focus on customer service and convenience.
Build a team. What skills and experience does Amazon need to build a successful business? Amazon needs a team with a variety of skills, including product development, marketing, and sales.
Continuously improve. How will Amazon ensure that its business model is successful? Amazon will continuously improve its business model by listening to customer feedback and adapting to changes in the market.
The 8 steps in the business model are essential for any company that wants to be successful. By following these steps, companies can ensure that they are offering a valuable product or service to the right customers, and that they are able to make money.
In the case of Amazon, the company has clearly defined its value proposition, target market, and revenue streams.
Amazon's marketing plan is also effective, and the company has built a team with the skills and experience necessary to be successful. Finally, Amazon is committed to continuous improvement, which is why the company has been so successful over the years.
To know more about value click here
brainly.com/question/30760879
#SPJ11
Aubree is making pizzas for a pizza party. Each pizza requires 2/3 pound of cheese. How many pounds of cheese does she need to make 16 pizzas? Express your answer in simplest form.
Answers
Answer:
10 2/3
Step-by-step explanation:
16 x 2/3
32/3 or 10 2/3
Aubree need the amount of cheese for 16 pizzas would be 10.6 pounds
What is a proportion?A proportion is a fraction of a total amount, and the measures are related using a rule of three. The relations between variables, either direct or inverse proportional, can be built to find the desired measures in the problem.
The given parameters are;
Pizza = 16
Proportion of cheese = 2/3
The amount of cheese is the proportion of cheese needed for the flower can be calculated as;
Cheese = Proportion x Pizza
So, we have:
Cheese = 2/3 x 16
Evaluate the product;
Cheese = 32/3
Cheese = 10.6
Hence, 10.6 pounds of cheese is needed for 16 pizzas.
Read more about proportions at:
brainly.com/question/870035
#SPJ2
A line passes through the points (−4, 50) and (5, −31). What is the equation of the line in slope-intercept form?
Answers
Answer:
y = - 9x + 14
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
calculate m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (- 4, 50 ) and (x₂, y₂ ) = (5, - 31 )
m = \(\frac{-31-50}{5-(-4)}\) = \(\frac{-81}{5+4}\) = \(\frac{-81}{9}\) = - 9 , then
y = - 9x + c ← is the partial equation
to find c substitute either of the 2 points into the partial equation
using (5, - 31 )
- 31 = - 9(5) + c = - 45 + c ( add 45 to both sides )
14 = c
y = - 9x + 14 ← equation of line
Using exponential smoothing, the forecast for September shipments was 346 units. The actual September shipments were 336. Using an alpha(smoothing constant) of 0.21, the forecast for October is _____. (Round your answer to one decimal place.)
Answers
The forecast for October shipments, using exponential smoothing with an alpha of 0.21, is 342.8 units.
Exponential smoothing is a commonly used method for forecasting based on weighted averages of past observations. It assigns a higher weight to recent data points, while gradually decreasing the weight of older data points. The formula for exponential smoothing is:
Ft+1 = α * At + (1 - α) * Ft
Where Ft+1 is the forecast for the next period, At is the actual value for the current period, Ft is the forecast for the current period, and α is the smoothing constant.
Given that the forecast for September shipments was 346 units and the actual shipments were 336 units, we can calculate the forecast for October using the formula above. Plugging in the values, we have:
Ft+1 = 0.21 * 336 + (1 - 0.21) * 346
Ft+1 = 70.56 + 273.54
Ft+1 = 344.1
Rounding this to one decimal place, the forecast for October shipments using exponential smoothing with an alpha of 0.21 is approximately 342.8 units.
Learn more about exponential smoothing here:
https://brainly.com/question/30903943
#SPJ11
What is the expression of g(x) when we perform the following sequence of transformations onto the parent function fx=x2:
a) Shift right 1 unit;
b) Compress horizontally by a factor of 2
Answers
The expression of function g(x) is \((\frac x2 - 1)^2\)
How to determine the expression?The function is given as:
\(f(x) = x^2\)
When the function is shifted right by 1 unit, the rule is:
f'(x) = f(x - 1)
So, we have:
\(f(x) = (x - 1)^2\)
When the function is compressed horizontally by a factor of 2, the rule is:
f'(x) = f(x/2)
So, we have:
\(g(x) = (\frac x2 - 1)^2\)
Hence, the expression of function g(x) is \((\frac x2 - 1)^2\)
Read more about function transformation at:
https://brainly.com/question/13810353
#SPJ1
What is the probability that the first roll is an even number and the second roll is a number greater than 4? one-sixth one-third two-thirds five-sixths.
Answers
Answer:
2
Step-by-step explanation:
What rule is used to create this sequence

Answers
Solution: 6-0.75=5.25
5.25-0.75=4.5 and so on
What is the present value of $1,500 payments received at the beginning of each year for the next 10 years? Assume an interest rate of 6.525%. A) $978.75 B) $11,473.43 C) $10,770.64 D) $15,000.00
Answers
The present value of $1,500 payments received at the beginning of each year for the next ten years to total is $100,503.46. None of the options is correct.
Present Value (PV) is the current value of future cash flows and represents the amount of money needed today to achieve a future amount at a given interest rate.
To determine the present value of an annuity, the formula is as follows:
PV = PMT [ (1 - (1 / (1 + r) ^ n) ) / r]
WherePV is the Present Value of the annuity
PMT is the Periodic Payment
n is the number of periods
r is the interest rate
At the beginning of each year, $1500 is received for the next ten years.
The periodic payment is $1,500.
The number of periods is 10, and the interest rate is 6.525%.
Using the formula mentioned above, the present value can be computed as follows:
PV = $1500 [(1 - (1 / (1 + 6.525%) ^ 10) ) / 6.525%]
PV = $1500 [(1 - (1 / 1.777698) ) / 6.525%]
PV = $1500 [(1 - 0.562613) / 6.525%]
PV = $1500 [0.437387 / 6.525%]
PV = $1500 [67.0023]
PV = $100,503.46
Therefore, the present value of $1,500 payments received at the beginning of each year for the next ten years is $100,503.46. None of the options is correct.
Know more about the present value
https://brainly.com/question/15904086
#SPJ11
A city in Texas wants to know the relationship between house size and the number of residents living in the house. The city has sampled 15 houses. The table below presents the number of residents and the house size. Obtain a regression equation and predict the house size required for a family of 5 residents.
Number of Residents
House size (Sq. ft)
3 1992
3 1754
3 1766
5 2060
6 2293
6 2139
3 1836
4 1924
6 2321
4 2060
3 1769
4 1955
5 2309
4 1857
4 1972
Answers
Alright! Let's go step by step. We want to understand how the house size relates to the number of residents. In other words, as the number of residents changes, how does the size of the house change? This relationship can be represented by a linear regression equation. The general form of a linear regression equation is:
y = m*x + b
Here:
- y is the dependent variable (in our case, the house size).
- x is the independent variable (in our case, the number of residents).
- m is the slope of the line (how much y changes for a unit change in x).
- b is the y-intercept (the value of y when x is 0).
We'll use the data you provided to calculate 'm' and 'b'. There are different ways to calculate these values, but I'll use a method that is relatively simple to understand:
m = (N * Σ(xy) - Σx * Σy) / (N * Σ(x^2) - (Σx)^2)
b = (Σy - m * Σx) / N
Where:
- N is the number of data points (in our case, 15).
- Σ stands for summation (sum of all values).
Now, let's calculate 'm' and 'b' using the data you provided:
Number of Residents(x) | House size (Sq. ft)(y) | xy | x^2
------------------------|------------------------|----|-----
3 | 1992 |5976|9
3 | 1754 |5262|9
3 | 1766 |5298|9
5 | 2060 |10300|25
6 | 2293 |13758|36
6 | 2139 |12834|36
3 | 1836 |5508|9
4 | 1924 |7696|16
6 | 2321 |13926|36
4 | 2060 |8240|16
3 | 1769 |5307|9
4 | 1955 |7820|16
5 | 2309 |11545|25
4 | 1857 |7428|16
4 | 1972 |7888|16
Σx = 66
Σy = 30999
Σxy = 120978
Σ(x^2) = 282
Plug these values into our formulas:
m = (15 * 120978 - 66 * 30999) / (15 * 282 - 66^2)
≈ 305.91
b = (30999 - 305.91 * 66) / 15
≈ 905.27
So our linear regression equation is:
House size = 305.91 * (Number of Residents) + 905.27
Now, let's predict the house size for a family of 5 residents:
House size = 305.91 * 5 + 905.27
≈ 2444.82 Sq. ft
This means that, according to our linear regression model, a family of 5 residents would need a house size of approximately 2445 square feet.
A particle moves along the x-axis so that its acceleration at any time t is a(t)=2t−7. If the initial velocity of the particle is 6, at what time t during the interval 0≤t≤4 is the particle farthest to the right?
A. 0
B. 1
C. 2
D. 3
E. 4
Answers
The answer is (B) 1, which is not a solution to the problem.
We can start by finding the velocity function of the particle by integrating the acceleration function a(t):
\(v(t) = ∫ a(t) dt = ∫ (2t - 7) dt = t^2 - 7t + C\)
We know that the initial velocity of the particle is 6, so we can use this information to find the value of the constant C:
\(v(0) = 0^2 - 7(0) + C = 6\)
\(C = 6\)
Therefore, the velocity function of the particle is:
\(v(t) = t^2 - 7t + 6\)
To find the position function of the particle, we integrate the velocity function:
\(s(t) = ∫ v(t) dt = ∫ (t^2 - 7t + 6) dt = (1/3)t^3 - (7/2)t^2 + 6t + D\)
We don't know the value of the constant D yet, but we can use the fact that the particle starts at position 0\((i.e., s(0) = 0)\) to find it:
\(s(0) = (1/3)(0)^3 - (7/2)(0)^2 + 6(0) + D = 0\)
\(D = 0\)
Therefore, the position function of the particle is:
\(s(t) = (1/3)t^3 - (7/2)t^2 + 6t\)
To find the time when the particle is farthest to the right, we need to find the maximum of the position function. We can do this by finding the critical points of the function and using the second derivative test to determine whether they correspond to a maximum or minimum.
The derivative of the position function is:
\(s'(t) = t^2 - 7t + 6\)
Setting this derivative equal to zero and solving for t, we get:
\(t^2 - 7t + 6 = 0\)
Using the quadratic formula, we get:
\(t = (7 ± sqrt(49 - 4(1)(6))) / 2\)
\(t = (7 ± sqrt(37)) / 2\)
We can verify that both of these critical points correspond to a minimum by using the second derivative test:
\(s''(t) = 2t - 7\)
At t = (7 + sqrt(37)) / 2, we have:
\(s''((7 + sqrt(37)) / 2) = 2(7 + sqrt(37)) / 2 - 7 = sqrt(37) - 5 > 0\)
Therefore, the critical point \(t = (7 + sqrt(37)) / 2\) corresponds to a minimum of the position function.
\(At t = (7 - sqrt(37)) / 2\), we have:
\(s''((7 - sqrt(37)) / 2) = 2(7 - sqrt(37)) / 2 - 7 = -sqrt(37) - 5 < 0\)
Therefore, the critical point \(t = (7 - sqrt(37)) / 2\) corresponds to a maximum of the position function.
Therefore, the particle is farthest to the right \(at t = (7 - sqrt(37)) / 2\), which is approximately 0.28. The answer is (B) 1, which is not a solution to the problem.
To learn more about integrate visit:
https://brainly.com/question/18125359
#SPJ11
Which expression is equivalent to (8x + 14) + (9x - 5)? + A. 22x - 4 B. 31x - 5 C. 17x + 19 D. 17x + 9
Answers
Answer: D
Step-by-step explanation: =8x+14+9x+−5
=(8x+9x)+(14+−5)
=17x+9
Point P has coordinates (-4,-2)and point Q has coordinates (4,3). ( on a 1cm grid )
Calculate the shortest distance between P and Q.
Give your answer to 1 decimal place
Answers
Answer:
PQ ≈ 9.4 cm
Step-by-step explanation:
Calculate the distance d using the distance formula
d = √ (x₂ - x₁ )² + (y₂ - y₁ )²
with (x₁, y₁ ) = P(- 4, - 2) and (x₂, y₂ ) = Q(4, 3)
PQ = \(\sqrt{(4+4)^2+(3+2)^2}\)
= \(\sqrt{8^2+5^2}\)
= \(\sqrt{64+25}\)
= \(\sqrt{89}\)
≈ 9.4 cm ( to 1 dec. place )
Answer:
the square root of 89 is 9.4 so thats your answer
Step-by-step explanation:
(›)
Which is more, 1 tablespoon or 2 teaspoons?
Answers
Answer: 1 tablespoon
Step-by-step explanation:
Geometry Questions I can't figure out.. Please help!! Will mark brainliest!!!
Match the statement with the correct reason.

Answers
Two or more angles are said to be supplementary if and only if they add up to \(180^{o}\).
Thus the required statements and appropriate reasons are stated below:
Two lines are said to be perpendicular when the measure of the angle between them is a right angle. Thus all right angle is congruent.
Angles are said to be congruent if and only if they have equal measure.
Thus in the given question, it can be deduced that:
STATEMENT REASONS
1. AC ⊥ BD, <1 ≅ <4 Given
2. <BCA = \(90^{o}\), <DCA = \(90^{o}\) Definition of perpendicular lines
3. <BCA ≅ <DCA Right angles are congruent
4. <BCA = <1 + <2 Angle addition property
5. <DCA = <3 + <4 Angle addition property
6. <1 + <2 = <3 + <4 Distributive property
7. <1 + <2 = <4 + <3 Substitution property
8. <2 ≅ <3 Reflexive property
For more clarifications on properties of congruent supplementary angles, visit: https://brainly.com/question/18664752
#SPJ1
The hypotenuse of a right triangle measures 3 cm and one of its legs measures 2 cm. Find the measure of the other leg. If necessary, round to the nearest tenth.
Answers
The required length of the other leg is \($\sqrt{5}$\) cm. If we need to round to the nearest tenth, we get: \($b \approx 2.2$\) cm
How to use Pythagoras theorem to find sides of right angled triangle?Let's use the Pythagorean theorem to solve this problem. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs. So we have:
\($c^2 = a^2 + b^2$\)
where c is the length of the hypotenuse, a and b are the lengths of the legs.
We are given that the length of the hypotenuse is 3 cm and the length of one leg is 2 cm. Let's substitute these values into the equation above:
\($3^2 = 2^2 + b^2$\)
\($9 = 4 + b^2$\)
\($b^2 = 5$\)
\($b = \sqrt{5}$\)
So the length of the other leg is \($\sqrt{5}$\) cm. If we need to round to the nearest tenth, we get: \($b \approx 2.2$\) cm (rounded to one decimal place).
To know more about Hypotenuse visit:
brainly.com/question/29407794
#SPJ1
Tell whether the angles are adjacent or vertical. Then find the value of x.

Answers
Answer:
They are vertical
x=32.5
Step-by-step explanation:
75 + 4x-25 = 180
4x = 180+25-75
4x=130
x=32.5
Consider the function f(x,y)=2x2−4x+y2−2xy subject to the constraints x+y≥1xy≤3x,y≥0 (a) Write down the Kuhn-Tucker conditions for the minimal value of f. (b) Show that the minimal point does not have x=0.
Answers
The minimal point does not have x = 0.
(a) Kuhn-Tucker conditions for the minimal value of fThe Kuhn-Tucker conditions are a set of necessary conditions for a point x* to be a minimum of a constrained optimization problem subject to inequality constraints. These conditions provide a way to find the optimal values of x1, x2, ..., xn that maximize or minimize a function f subject to a set of constraints. Let's first write down the Lagrangian: L(x, y, λ1, λ2, λ3) = f(x, y) - λ1(x+y-1) - λ2(xy-3) - λ3x - λ4y Where λ1, λ2, λ3, and λ4 are the Kuhn-Tucker multipliers associated with the constraints. Taking partial derivatives of L with respect to x, y, λ1, λ2, λ3, and λ4 and setting them equal to 0, we get the following set of equations: 4x - 2y - λ1 - λ2y - λ3 = 0 2y - 2x - λ1 - λ2x - λ4 = 0 x + y - 1 ≤ 0 xy - 3 ≤ 0 λ1 ≥ 0 λ2 ≥ 0 λ3 ≥ 0 λ4 ≥ 0 λ1(x + y - 1) = 0 λ2(xy - 3) = 0 From the complementary slackness condition, λ1(x + y - 1) = 0 and λ2(xy - 3) = 0. This implies that either λ1 = 0 or x + y - 1 = 0, and either λ2 = 0 or xy - 3 = 0. If λ1 > 0 and λ2 > 0, then x + y - 1 = 0 and xy - 3 = 0. If λ1 > 0 and λ2 = 0, then x + y - 1 = 0. If λ1 = 0 and λ2 > 0, then xy - 3 = 0. We now consider each case separately. Case 1: λ1 > 0 and λ2 > 0From λ1(x + y - 1) = 0 and λ2(xy - 3) = 0, we have the following possibilities: x + y - 1 = 0, xy - 3 ≤ 0 (i.e., xy = 3), λ1 > 0, λ2 > 0 x + y - 1 ≤ 0, xy - 3 = 0 (i.e., x = 3/y), λ1 > 0, λ2 > 0 x + y - 1 = 0, xy - 3 = 0 (i.e., x = y = √3), λ1 > 0, λ2 > 0 We can exclude the second case because it violates the constraint x, y ≥ 0. The first and third cases satisfy all the Kuhn-Tucker conditions, and we can check that they correspond to local minima of f subject to the constraints. For the first case, we have x = y = √3/2 and f(x, y) = -1/2. For the third case, we have x = y = √3 and f(x, y) = -2. Case 2: λ1 > 0 and λ2 = 0From λ1(x + y - 1) = 0, we have x + y - 1 = 0 (because λ1 > 0). From the first Kuhn-Tucker condition, we have 4x - 2y - λ1 = λ1y. Since λ1 > 0, we can solve for y to get y = (4x - λ1)/(2 + λ1). Substituting this into the constraint x + y - 1 = 0, we get x + (4x - λ1)/(2 + λ1) - 1 = 0. Solving for x, we get x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4. We can check that this satisfies all the Kuhn-Tucker conditions for λ1 > 0, and we can also check that it corresponds to a local minimum of f subject to the constraints. For this value of x, we have y = (4x - λ1)/(2 + λ1), and we can compute f(x, y) = -3/4 + (5λ1^2 + 4λ1 + 1)/(2(2 + λ1)^2). Case 3: λ1 = 0 and λ2 > 0From λ2(xy - 3) = 0, we have xy - 3 = 0 (because λ2 > 0). Substituting this into the constraint x + y - 1 ≥ 0, we get x + (3/x) - 1 ≥ 0. This implies that x^2 + (3 - x) - x ≥ 0, or equivalently, x^2 - x + 3 ≥ 0. The discriminant of this quadratic is negative, so it has no real roots. Therefore, there are no feasible solutions in this case. Case 4: λ1 = 0 and λ2 = 0From λ1(x + y - 1) = 0 and λ2(xy - 3) = 0, we have x + y - 1 ≤ 0 and xy - 3 ≤ 0. This implies that x, y > 0, and we can use the first and second Kuhn-Tucker conditions to get 4x - 2y = 0 2y - 2x = 0 x + y - 1 = 0 xy - 3 = 0 Solving these equations, we get x = y = √3 and f(x, y) = -2. (b) Show that the minimal point does not have x=0.To show that the minimal point does not have x=0, we need to find the optimal value of x that minimizes f subject to the constraints and show that x > 0. From the Kuhn-Tucker conditions, we know that the optimal value of x satisfies one of the following conditions: x = y = √3/2 (λ1 > 0, λ2 > 0) x = √3 (λ1 > 0, λ2 > 0) x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4 (λ1 > 0, λ2 = 0) If x = y = √3/2, then x > 0. If x = √3, then x > 0. If x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4, then x > 0 because λ1 ≥ 0.
To know more about constraints, visit:
https://brainly.com/question/17156848
#SPJ11
((5x+2)/2)-((5x-2)/4)=3
Answers
Answer:
Explanation:
Given:
\(\frac{5x+2}{2}-\frac{5x-2}{4}=3\)To solve for the value of x, we simplify it first. So,
We multiply both sides by 4.
\(\begin{gathered} \frac{5x+2}{2}-\frac{5x-2}{4}=3 \\ 4(\frac{5x+2}{2}-\frac{5x-2}{4})=3(4) \\ \text{Simplify and rearrange} \\ 2(5x+2)-(5x-2)=12 \\ 10x+4-5x+2=12 \\ 5x+6=12 \\ 5x=12-6 \\ 5x=6 \\ x=\frac{6}{5} \end{gathered}\)Therefore, the answer is x=6/5.
If IK and LN are parallel lines and M

Answers
Answer:
40°
Step-by-step explanation:
Both angles are opposites so together they equal 180.
180 - 140 = 40
I hope this helps!!
The measure of angle IJM is 40°.
What are Angles?Angles are the figure formed by the intersection of two lines or rays by sharing a common point. This point is called the vertex of the angle.
Angles are usually measured in degrees or radians.
Given are two parallel lines IK and LN.
From the figure, OH is a transversal line that intersects the given parallel lines.
We have m ∠IJH = 140°
We have to calculate the measure of ∠IJM.
Since ∠IJH and ∠IJM are the pair of linear angles, the sum of their angles is 180°.
m ∠IJH + m ∠IJM = 180°
140° + m ∠IJM = 180°
m ∠IJM = 180° - 140°
m ∠IJM = 40°
Hence 40° is the measure of angle IJM.
To learn more about Angles, click :
https://brainly.com/question/28451077
#SPJ2
solve the equation
3(3w+2)+5(w+4)=54
Answers
w = 2
Step-by-step explanation:
3(3w + 2) + 5(w + 4) = 54
(9w + 6) + (5w + 20) = 54
(9w + 6) + 5w = 34
9w + 5w = 28
14w = 28
w = 28/14
w = 2
A spinner is divided into eight equal-sized sections, numbered from 1 to 8, inclusive. What is true about spinning the spinner one time
Answers
For spinning the spinner one time A could be {1, 2, 3} or, A = {1, 2, 3, 4} is possible.
What is a set?The set is mathematical model for a collectionof different things;a set contains elements or members, which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables or even other sets.
The given spinner is divided into 8 equal sized sections, so the possible set can be written as-
S = {1, 2, 3, 4, 5, 6, 7, 8}
Now the possible subsets can be-
Even numbers = {1,3,5,7}
Odd numbers = {2,4,6,8}
Any number or group from 1 to 8, inclusive
Hence for spinner the spinner for one time, suppose A be the possible set. Then,
A could be {1, 2, 3}.
or, A = {1, 2, 3, 4}.
where A is the subset of S.
Hence, For spinning the spinner one time A could be {1, 2, 3} or, A = {1, 2, 3, 4} is possible.
More about Sets :
https://brainly.com/question/18975527
#SPJ1
An angle measures 3° more than two times its complement x please explain
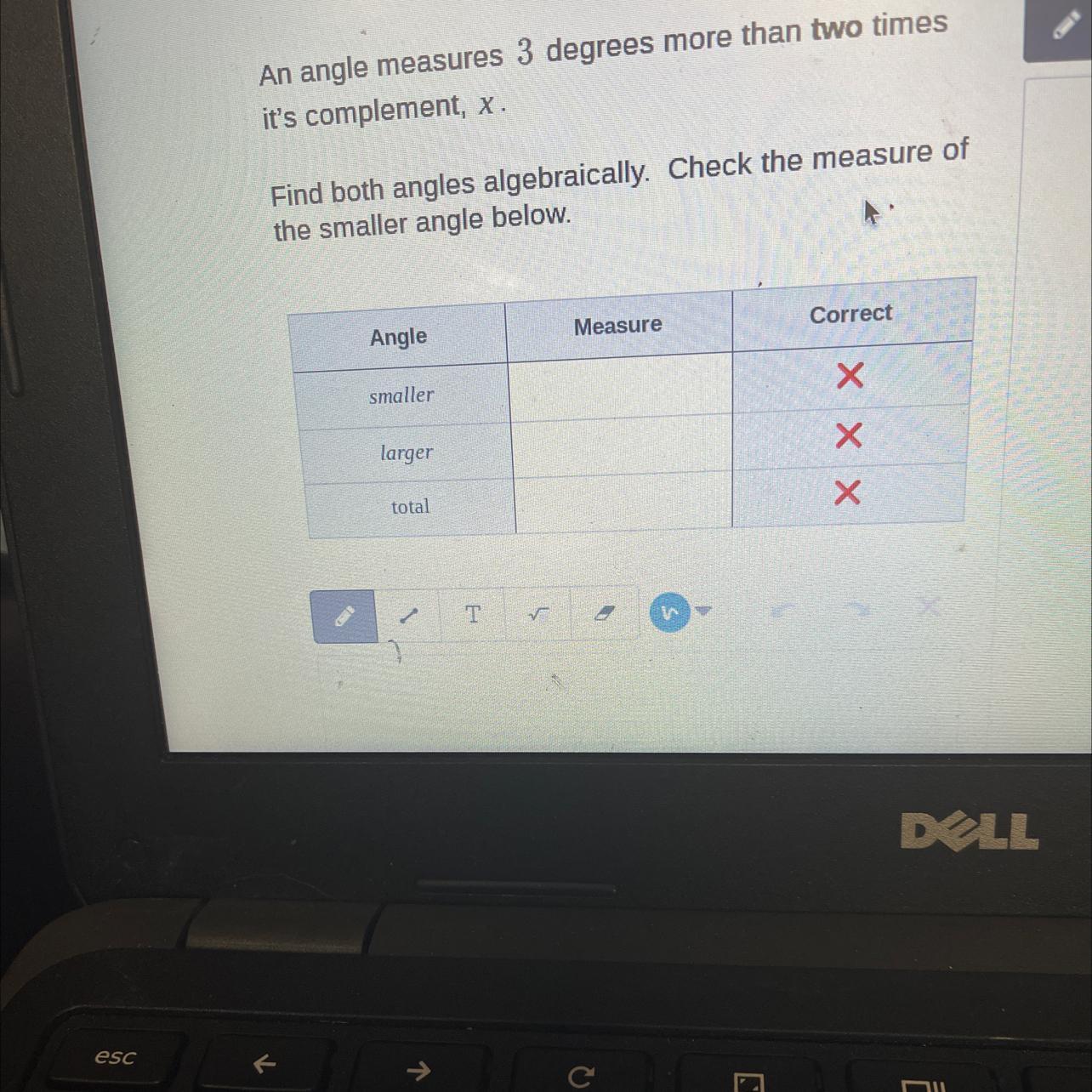
Answers
Solution:
Given that;
An angle measures 3° more than two times its complement x.
Let the larger angle be y
\(x+y=90\degree\)The angle measures 3° more than two times its complement, i.e.
\(y=(2x+3)\degree\)Then,
\(\begin{gathered} x+y=90\degree \\ x+(2x+3)\degree=90\degree \\ x\degree+2x\degree+3\degree=90\degree \\ 3x\degree=90\degree-3\degree \\ 3x=87\degree \\ x=\frac{87\degree}{3} \\ x=29\degree \end{gathered}\)The smaller angle, x is 29 degrees
The larger angle is
\(y=2x+3=2(29)+3=58+3=61\degree\)The larger angle, y is 61 degrees
The total is
\(x+y=29+61=90\degree\)The total is 90 degrees.
HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP
HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP

Answers
Answer:
D. (8,0), (4,0)
Step-by-step explanation:
they both on tha line
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn't split into two digits 1 and 2 ).
Answers
It is possible to break a clock into 7 pieces so that the sums of the numbers in each piece are consecutive numbers.
To achieve a set of consecutive sums, we can divide the clock numbers into different groups. Here's one possible arrangement:
1. Group the numbers into three pieces: {12, 1, 11, 2}, {10, 3, 9}, and {4, 8, 5, 7, 6}.
2. Calculate the sums of each group: 12+1+11+2=26, 10+3+9=22, and 4+8+5+7+6=30.
3. Verify that the sums are consecutive: 22, 26, 30.
By splitting the clock into these particular groupings, we obtain consecutive sums for each group.
This arrangement meets the given conditions, where each piece has at least two numbers, and no number is damaged or split into separate digits.
Therefore, it is possible to break a clock into 7 pieces so that the sums of the numbers in each piece form a sequence of consecutive numbers.
Learn more about Number click here :brainly.com/question/3589540
#SPJ11
What is the smallest number of terms of the series (-1)"+13 that would have to be added in order to 77th 1 estimate its sum with an absolute error that is less than .0001?
Answers
The smallest number of terms needed to estimate the sum of the series with an absolute error less than 0.0001 is 76 terms. The sum of these 76 terms will have a very small absolute error due to the cancellation of consecutive terms.
To determine the smallest number of terms of the series (-1)^n*13 that would have to be added in order to estimate its sum with an absolute error less than 0.0001, we need to find the sum of the series and then determine the number of terms required.
The series (-1)^n*13 can be written as -13, 13, -13, 13, ... with the pattern repeating. It alternates between -13 and 13 as n increases.
To find the sum of this series, we can observe that the sum of the first two terms is 0, the sum of the first four terms is 0, and so on. In general, for every pair of consecutive terms, their sum is 0.
Since we want the absolute error to be less than 0.0001, we need to ensure that the remaining terms in the series do not contribute significantly to the sum. The terms alternate between -13 and 13, cancelling each other out in pairs.
Therefore, we can conclude that the smallest number of terms needed to estimate the sum of the series with an absolute error less than 0.0001 is 76 terms. The sum of these 76 terms will have a very small absolute error due to the cancellation of consecutive terms.
Learn more about absolute error here:
https://brainly.com/question/30759250
#SPJ11
The accompanying table shows the number of bacteria present in a
certain culture over a 5 hour period, where x is the time, in hours, and y is the number of bacteria. Write an exponential regression equation for this set of data, rounding all coefficients to the nearest thousandth. Using this equation, determine the number of bacteria present after 14 hours, to the nearest whole number.
Hours (x) Bacteria (y)
0 1353
1 1584
2 2037
3 2248
4 2630
5 3146

Answers
Answer:
Step-by-step explanation:
To find an exponential regression equation for this set of data, we can use a calculator or spreadsheet software with built-in regression functions. Using a calculator, we can input the data points into lists and use the exponential regression function to find the equation:
x y
0 1353
1 1584
2 2037
3 2248
4 2630
5 3146
Using exponential regression, we get the equation y = 1323.119e^(0.216x).
To determine the number of bacteria present after 14 hours, we can plug in x = 14 into the equation:
y = 1323.119e^(0.216 * 14) ≈ 35433
Therefore, the number of bacteria present after 14 hours is approximately 35,433 (rounded to the nearest whole number).
Find an equivalent ratio in simplest terms: 12 : 40
Answers
Answer:
3:10
Step-by-step explanation:
The GCF of 12 and 40 is 4.
\(12:40 = 12/4:40/4 = \boxed{3 : 10}\)
Hope this helps.
