Factorise -75ab² - 15ac
5a(3b - c)
-15b²(3a + c)
-15a(5b² + c)
15a(5b² - c)
A triangle has a base of length 6 cm and an area of less than 12 cm². Which of the following gives the height h of the triangle
h < 4 cm
h < 6cm
h < 12 cm
h < 24 cm
Expand (2x-3)(2x +3)
4x² + 12x + 9
4x² - 12x – 9
4x² - 9
4x² + 9
A woman buys 8 tubers of yam at #200 each and sells them at a profit of 12%. Calculate the selling price.
#192
#1600
#1792
#2000
What is the size of each angle of a regular 15-sided polygon?
78⁰
156⁰
185⁰
200⁰
The height of a boy is t cm. His father is two times his height. Express the height of the father in terms of t.
5t cm
2t cm
t cm
t² cm
Factorise 4am² - 6am
2am(2m – 3)
m²(2a - 3m)
am²(4 - 6a)
2a²m²(2m - 3)
What is the slant height of a cone of height 8cm and base diameter of 12cm?
5 cm
6 cm
8 cm
10 cm
Express 51 x 10⁻⁵ as a decimal number.
0•000051
0•00051
0•0051
0•51
A television costs #54 000. A 12¹/₂% discount is given for cash. What is the cash price ?
# 54 000
# 47 000
# 47 250
# 6 750
Find y-intercept in the graph below

(0, 1)
(0, 5)
(5, 0)
(0, 2)
Simplify - 40pq ÷ (-2)²
-10p
-10q
-10pq
10pq
Express the product of 0•003 and 0•045 in standard form.
3•45 x 10⁵
1•35 x 10⁵
1•35 x 10⁻⁵
1•35 x 10⁻⁴
Submission Tracking ID - DO NOT CHANGE *
This is important for tracking purposes. Do not change. Any change in this will make your submission void
Which of these is the three figure bearing of the acute-angle bearing N40⁰W ?
320⁰
310⁰
270⁰
040⁰
The volume of a cylinder is 700π cm³. What is the base diameter of the cylinder if its height is 7 cm ?
6•5 cm
7cm
10 cm
20 cm
What is the LCM of 2x²y, 3xy² and 4x²y ?
16x²y²
12x²y²
12x²y
7xy
Express 636 000 in standard form.
6.36 x 10⁻⁵
6.36 x 10⁻⁴
6.36 x 10⁴
6.36 x 10⁵
A cone and a cylinder have equal volumes and radii. The height of the cone is 12 cm. What is the height of the cylinder?
4 cm
12 cm
36 cm
50 cm
Find the angle measured clockwise between the directions: N and SW
45°
135°
180°
225°
What is the total surface area of a cylinder opened at one end if its height is 20cm and it's diameter is 14cm (π = 3¹/₇)
880 cm²
1034 cm²
1188 cm²
1250 cm²
I think of a number. I then double it. The result is 58. What number did I think of ?
29
20
16
10
RSTU is a quadrilateral as seen below. What is the value of X?

5
10
11
15
Answers
Answer:
9) 51 × 10⁻⁵ = 0.00051
10) Cash price = #54,000 × (1 - 0.125) = #47,250
11) -40·p·q÷(-2)² = -10·p·q
12) 0.003 × 0.045 = 1.35 × 10⁻⁴
13) N40°W = 320°
14) The base diameter of the cylinder = √(4 × (700×π cm³/7)/π) = 20 cm
15) The LCM of 2·x²·y, 3·x·y² is 12·x²·y²
16) 636,000 = 6.36 × 10⁵
17) 1/3·π·r²·h₁ = π·r²·h₂
h₂/h₁ = 1/3·π·r²/( π·r²) = 1/3
h₂/12 = 1/3
h₂ = 12/3 = 4 cm, the height of the cylinder = 4 cm
18) The angle = 180 + 45 = 225°
19) The total surface area = 22/7×14²/4 + 22/7 ×14 × 20 = 1034 cm²
20) The number is 58/2 = 29.
Step-by-step explanation:
Step-by-step explanation:
THE ANSWERS ARE
1 B
2A
3C
4A
6B
Related Questions
Lin has a drawing with an area of 20 square inches. If she increases all the sides by a scale factor of 4, what will the new area be in square inches?
Answers
Answer:
100 square inches
Step-by-step explanation:
20*4=100
Mr. Brown purchased tires for his car. The tires were $75 each, including tax, plus $10 for installation. Mr. Brown paid $160 for the tires and installation. Which equation can be used to find the number of tires, t, that Mr. Brown purchased?
A. t = 160 + 75(10)
B. 75 + t(10) = 160
C. 75t + 10 =160
D. 160t - 75 = 10
Could you show your work? Thanks!
Answers
Answer:
Step-by-step explanation:
The answer is C because t = 2 so 75x2=150 and 150 + 10= 160.
What is the ratio of the length of one leg to the length of the other leg?

Answers
9514 1404 393
Answer:
D. 1 : 1
Step-by-step explanation:
The ratio of the two legs in any isosceles triangle is 1 : 1. That is also true of this isosceles right triangle. (You can tell it is isosceles because the acute angles are identical in size.)
Write a system of equations for the following word problem. Solve. What does your solution mean in the context of the question?
The wedding planner was looking for the best deal on flowers. Flowers R’ Us was selling roses for $2 each and then $150 for delivery. Flowers Lobby are selling roses for $4 each and $140 for delivery. At how many flowers and at what cost will the two flower shops be the same?
Answers
The pricing and flowers from both businesses will be the same at 5 flowers and 160 dollars.
Let x be the number of flowers ordered from both shops at the same cost.
For R'U shop,
Total cost = Per flower cost + delivery charges
Total cost = 2*x+150
For Flowers Lobby,
Total cost = Per flower cost + delivery charges
Total cost = 4*x+140
Thus, for the same cost, the value of x will be,
4x+140= 2x+150
2x = 10
x=5
Therefore, for 5 flowers and 160$, the price and the flowers will be equal from both shops.
Learn more about the System of equations here:
https://brainly.com/question/12628931
#SPJ1
In a class of 34 students, 19 of them are girls.
What percentage of the class are girls?
Give your answer to 1 decimal place
Answers
Step-by-step explanation:
Since we have given that
Total no. if students= 34
no. of girls = 19
so, percentage of the class are girls is given by
\( \frac{number \: of \: girls}{total \: number \: of \: students} = \frac{19}{34} \times 100 \\ = 55.88 \: percentage\)
the annual precipitation amounts in a certain mountain range are normally distributed with a mean of 90 inches, and a standard deviation of 14 inches. what is the probability that the mean annual precipitation of a sample of 49 randomly picked years will be less than 92.8 inches?
Answers
The probability that the mean annual precipitation of a sample of 49 randomly picked years will be less than 92.8 inches is, 0.9192
What is standard deviation?
The standard deviation in statistics is a measurement of how much a group of values can vary or be dispersed. A low standard deviation suggests that values are often close to the set's mean, whereas a large standard deviation suggests that values are dispersed over a wider range.
Given: The annual precipitation amounts in a certain mountain range are normally distributed with a mean of 90 inches, and a standard deviation of 14 inches.
z score is given by,
z = (x - μ)/(σ/√n) = (92.8 - 90)/(14/√49) = 2.8/2 = 1.4
The required probability is,
p(z < 1.4) = 0.9192, by standard normal table.
Hence, the probability that the mean annual precipitation of a sample of 49 randomly picked years will be less than 92.8 inches is, 0.9192.
To know more about the standard deviation, click on the link
https://brainly.com/question/475676
#SPJ4
According to the Chronicles of Contrived Statistics (March, 2016), the probability that Elon Musk will offer you a free trip into space in the next month is 41%. The probability that scientists from Area 51 will start selling pet aliens next month is 27%. Finally, the probability that either Elon Musk will offer you a free trip to space or that scientists will begin sales of pet aliens next month is 24%. What is the probability that both Elon Musk will offer you a free trip into space and scientists from Area 51 will start selling pet aliens in the next month?
Answers
Answer:
\(P(A\ and\ B) = 44\%\)
Step-by-step explanation:
Given
Represents the event as follows:
A = \(Elon\ Musk\) will offer you a \(free\ trip\) into space in the next month\
B = Scientists from \(Area\ 51\) will \(start\ selling\) pet aliens next month
So, we have:
\(P(A) = 41\%\)
\(P(B) = 27\%\)
\(P(A\ or\ B) = 24\%\)
Required
Determine \(P(A\ and\ B)\)
This is calculated as:
\(P(A\ and\ B) = P(A) + P(B) - P(A\ or\ B)\)
So, we have:
\(P(A\ and\ B) = 41\% + 27\% - 24\%\)
\(P(A\ and\ B) = 44\%\)
Which of the following shows the correct first step for finding the midpoint between the points (2,2) and (-1, 5)

Answers
Answer:
A
Step-by-step explanation:
By adding both the x and y coordinates individually and dividing them by two u get the mid point
The tree diagram below shows all of the possible outcomes for flipping three coins.
A tree diagram has outcomes (H, H, H), (H, H, T), (H, T, H), (H, T, T), (T, H, H), (T, H, T), (T, T, H), (T, T, T).
What is the probability that at least two of the coins will be tails?
Answers
Answer:
1/2
Step-by-step explanation:
Let H = the possible outcomes that include flipping heads
Let T = the possible outcomes that include flipping tails
In order to have an outcome of two coins having tails, that means for each outcome, you must have at least two T's.
Therefore, the possible outcomes are:
(H, T, T)
(T, H, T)
(T, T, H)
(T, T, T)
This is 4 possible outcomes, and since we want to find the probability we find the total number of outcomes and make a fraction.
\(4/8 = 1/2\)
There are 8 outcomes, and since 4 work for this scenario, the answer is 1/2.
#LearnWithBrainly
Find the slope and the equation of the tangent line to the graph of the function at the given value of x. y=x 4
−10x 2
+9;x=1 The slope of the tangent line is (Simplify your answer.) The equation of the tangent line is
Answers
The equation of the tangent line represents a straight line that passes through the point of tangency and has a slope of -16.
The slope of the tangent line to the graph of the function y = x^4 - 10x^2 + 9 at x = 1 can be found by taking the derivative of the function and evaluating it at x = 1. The equation of the tangent line can then be determined using the point-slope form.
Taking the derivative of the function y = x^4 - 10x^2 + 9 with respect to x, we get:
dy/dx = 4x^3 - 20x
To find the slope of the tangent line at x = 1, we substitute x = 1 into the derivative:
dy/dx (at x = 1) = 4(1)^3 - 20(1) = 4 - 20 = -16
Therefore, the slope of the tangent line is -16.
To find the equation of the tangent line, we use the point-slope form: y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope.
Given that the point of tangency is (1, y(1)), we substitute x1 = 1 and y1 = y(1) into the equation:
y - y(1) = -16(x - 1)
Expanding the equation and simplifying, we have:
y - y(1) = -16x + 16
Rearranging the equation, we obtain the equation of the tangent line:
y = -16x + (y(1) + 16)
To find the slope of the tangent line, we first need to find the derivative of the given function. The derivative represents the rate of change of the function at any point on its graph. By evaluating the derivative at the specific value of x, we can determine the slope of the tangent line at that point.
In this case, the given function is y = x^4 - 10x^2 + 9. Taking its derivative with respect to x gives us dy/dx = 4x^3 - 20x. To find the slope of the tangent line at x = 1, we substitute x = 1 into the derivative equation, resulting in dy/dx = -16.
The slope of the tangent line is -16. This indicates that for every unit increase in x, the corresponding y-value decreases by 16 units.
To determine the equation of the tangent line, we use the point-slope form of a linear equation, which is y - y1 = m(x - x1). We know the point of tangency is (1, y(1)), where x1 = 1 and y(1) is the value of the function at x = 1.
Substituting these values into the point-slope form, we get y - y(1) = -16(x - 1). Expanding the equation and rearranging it yields the equation of the tangent line, y = -16x + (y(1) + 16).
The equation of the tangent line represents a straight line that passes through the point of tangency and has a slope of -16.
To learn more about tangent click here:
brainly.com/question/10053881
#SPJ11
find a recurrence relation and give initial conditions for the number of bit strings of length n that do not have two consecutive 0s. how many such bit strings are there of length five?
Answers
there are 11 such valid strings.
To find the recurrence relation, let's consider the possibilities for the last digit of a valid bit string. It can either be 1 or 0. If it's 1, the remaining n-1 digits can be any valid bit string of length n-1. If it's 0, the second-to-last digit must be 1 to avoid having two consecutive 0s. In this case, the remaining n-2 digits can be any valid bit string of length n-2.
Therefore, the total number of valid bit strings of length n can be obtained by summing the number of valid strings of length n-1 (when the last digit is 1) and the number of valid strings of length n-2 (when the last digit is 0). This gives us the recurrence relation F(n) = F(n-1) + F(n-2).
For the initial conditions, we observe that F(1) = 2 because there are two valid bit strings of length 1: 0 and 1. Similarly, F(2) = 3 because there are three valid bit strings of length 2: 01, 10, and 11.
To find the number of valid bit strings of length five, we apply the recurrence relation iteratively. Starting with F(1) = 2 and F(2) = 3, we can compute F(3) = 5, F(4) = 8, and finally F(5) = 13. Therefore, there are 13 valid bit strings of length five.
Learn more about recurrence relation here:
https://brainly.com/question/30895268
#SPJ11
all other things being equal, what do you estimate the difference in traffic will be between a dealership in a suburban location compared to the traffic in a rural location? if you estimate that the traffic will be higher for a rural location, indicate a positive number; otherwise use a negative number.
Answers
Based on the given information "all other things being equal," we can estimate that the traffic will be higher for a dealership in a suburban location compared to a rural location. Therefore, we would estimate a positive number, indicating that the traffic in the suburban location is expected to be higher than in the rural location.
In general, a dealership in a suburban location tends to experience higher traffic compared to a rural location. This estimation is based on several factors. Suburban areas are typically more densely populated and have a higher concentration of residential and commercial activities, leading to increased overall traffic volume.
Additionally, suburban locations often have better transportation infrastructure, including highways, main roads, and public transportation options, which attract more commuters and potential customers to the area.
On the other hand, rural areas are characterized by lower population densities and fewer amenities, resulting in lower levels of traffic. Therefore, the estimate of a positive difference in traffic between a suburban and rural dealership is reasonable.
To learn more about traffic: https://brainly.com/question/9380087
#SPJ11
HELP. find the missing length indicated

Answers
The missing length of the given triangle is 28/3 which is equal to 9.3.
The Side-Splitters Theorem:
If BC is drawn parallel to DE and ADE is any triangle, then AB/BD = AC/CE
The parallelogram formed by the line BF and AE demonstrates that this is the case. BCEF
Triangles ABC and BDF are comparable because they have the same angles.
Side AB and Side AC are corresponding to Side BD and Side BF, respectively.
Thus, AB/BD = AC/BF while BF = CE
Hence, AB/BD = AC/CE.
Example:
When the lengths are doubled, the area is four times as large since the two triangles are comparable and have sides that are in the ratio 2:1.As a result, their area ratio is 4:1.4:1 can alternatively be written as 2^2:1.Then,
28/18 = x / 6
(14/9) * 6 = x
x = 28/3
x = 9.3
Hence, the missing length of the given triangle is 28/3 which is equal to 9.3.
To know more about Triangles check the below link:
https://brainly.com/question/385308
#SPJ1
Find the length of side x simplest radical form with a rational denominator

Answers
Answer:
The length of x in the simplest radical form with a rational denominator will be:
\(x=\frac{5\sqrt{3}}{2}\)Step-by-step explanation:
Given
hypotenuse = 5
angle Ф = 60°
To determine
x = ?
Using the trigonometric ratio
cos Ф = adjacent / hypotenuse
here
Ф = 60°
adjacent of 60° = x
hypotenuse = 5
so substituting Ф = 60°, adjacent = x and hypotenuse = 5 in the equation
cos Ф = adjacent / hypotenuse
so
\(cos\:60^{\circ }\:=\:\frac{x}{5}\)
\(\frac{\sqrt{3}}{2}=\frac{x}{5}\)
switch sides
\(\frac{x}{5}=\frac{\sqrt{3}}{2}\)
Multiply both sides by 5
\(\frac{5x}{5}=\frac{5\sqrt{3}}{2}\)
Simplify
\(x=\frac{5\sqrt{3}}{2}\)
Therefore, the length of x in the simplest radical form with a rational denominator will be:
\(x=\frac{5\sqrt{3}}{2}\)Can someone pose help me with this?

Answers
A car purchased for $25,000 is worth $23,750 after being used for one year. Find the percent decrease
A. 95%
B. 95%
C. 0. 5%
D. 5%
Answers
Answer:
0.95=95%
Step-by-step explanation:
25,000*0.95=23750
Square a root of 32761 by division method
Answers
Answer:
181..
Step-by-step explanation:
1 8 1 < answer
-----------
32761
1 1
227
28 224
361
361 361
3) (2 Marks) Find the range and codomain of the matrix transformation T A
, where A= \( {\left[\begin{array}{cc}1 & 2 \\ 1 & -2 \\ 0 & 1\end{array}\right] \). Is the result true if the functions are not linear? Justify your \( } \) answer.
Answers
T A can be seen as a linear transformation from R^2 to R^3.
To find the range and codomain of the matrix transformation T A, we need to first determine the matrix T A . The matrix T A is obtained by multiplying the input vector x by A:
T A (x) = A x
Therefore, T A can be seen as a linear transformation from R^2 to R^3.
To determine the range of T A , we need to find all possible outputs of T A (x) for all possible inputs x. Since T A is a linear transformation, its range is simply the span of the columns of A. Therefore, we can find the range by computing the reduced row echelon form of A and finding the pivot columns:
A = (\left[\begin{array}{cc}1 & 2 \ 1 & -2 \ 0 & 1\end{array}\right]) ~ (\left[\begin{array}{cc}1 & 0 \ 0 & 1 \ 0 & 0\end{array}\right])
The pivot columns are the first two columns of the identity matrix, so the range of T A is spanned by the first two columns of A. Therefore, the range of T A is the plane in R^3 spanned by the vectors [1, 1, 0] and [2, -2, 1].
To find the codomain of T A , we need to determine the dimension of the space that T A maps to. Since T A is a linear transformation from R^2 to R^3, its codomain is R^3.
If the functions were not linear, it would not make sense to talk about their range or codomain in this way. The concepts of range and codomain are meaningful only for linear transformations.
Learn more about linear from
https://brainly.com/question/2030026
#SPJ11
For the following ordered set of data, find the 60" percentile. 0,2,3,5,5, 6, 8, 10, 10, 11, 12, 14, 16 Click the answer you think is right. 8.4 6.0
Answers
To find the 60th percentile for the given set of data (0, 2, 3, 5, 5, 6, 8, 10, 10, 11, 12, 14, 16), the answer is 8.4.
To determine the 60th percentile, we need to arrange the data in ascending order. The ordered set of data is: 0, 2, 3, 5, 5, 6, 8, 10, 10, 11, 12, 14, 16.
To find the 60th percentile, we need to calculate the position of the value within the data set. Since the percentile represents the percentage of values below a certain point, we can calculate the position using the formula: (p/100) * (n + 1), where p is the percentile and n is the total number of data points.
For the 60th percentile, the calculation would be: (60/100) * (13 + 1) = 7.2. Since the position is not an integer, we can interpolate between the values. The value at the 7th position is 8, and the value at the 8th position is 10. By interpolating, we find that the 60th percentile is 8 + 0.2 * (10 - 8) = 8.4.
Therefore, the 60th percentile for the given set of data is 8.4.
To learn more about integer click here, brainly.com/question/490943
#SPJ11
A landscaping company charges a $12 fee to make a house call plus an hourly rate for labor. If the total bill for a job that takes 2.5 hours comes to $95.75, write an equation that can be used to solve for the hourly labor rate. Use r to represent the rate. Then solve the equation and explain all steps.
Answers
ATQ
\(\\ \tt\hookrightarrow 12+2.5r=95.75\)
\(\\ \tt\hookrightarrow 2.5r=95.75-12=83.75\)
\(\\ \tt\hookrightarrow r=83.75/2.5\)
\(\\ \tt\hookrightarrow r=33.5\)
50 points.
Please simplify.
Please answer it correctly and don't answer of you don't know otherwise I'll report it to higher authorities.

Answers
Answer:
1
Step-by-step explanation:
Using the rules of exponents
\((a^m)^{n}\) = \(a^{mn}\)
\(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
Given
\((\frac{1}{x^{(a-b)}) } ^{a+b}\) × \((\frac{1}{x^{b+a}) } ^{b-a}\)
= \(\frac{1}{x^{(a-b)(a+b)} }\) × \(\frac{1}{x^{(b+a)(b-a)} }\)
= \(\frac{1}{x^{(a^2-b^2)} }\) × \(\frac{1}{x^{(b^2-a^2)} }\)
= \(\frac{1}{x^{(a^2-b^2+b^2-a^2)} }\)
= \(\frac{1}{x^{0} }\)
= \(\frac{1}{1}\)
= 1
well you already got an answer so can i have free 25
I have to solve for x

Answers
X = 25
The two top angles both equal 60
Answer:
m<CAB = 59
m<ACB = 59
Step-by-step explanation:
4x - 41 = 2x + 9
2x - 41 = 9
2x = 50
x = 25
m<CAB: 4x - 41
4(25) - 41
59
m<ACB: 2x + 9
2(25) + 9
59
A box has the shape of a rectangular prism with height 31 cm. If the height is increased by 0.8 cm, by how much does the surface area of the box increase?
Use pencil and paper. Show your work. Then show a second way to solve the problem. Explain which way you like better and why.
Answers
First way to solve the problem: To find the increase in the surface area of the box, we need to calculate the difference in surface areas before and after the increase in height.
Let's denote the original height of the box as h1 = 31 cm and the increased height as h2 = 31 cm + 0.8 cm = 31.8 cm.
The surface area of a rectangular prism can be calculated using the formula: SA = 2lw + 2lh + 2wh, where l, w, and h represent the length, width, and height of the box, respectively.
Before the increase, the surface area (SA1) of the box is SA1 = 2lw + 2lh1 + 2wh1.
After the increase, the surface area (SA2) of the box is SA2 = 2lw + 2lh2 + 2wh2.
By subtracting SA1 from SA2, we can find the increase in surface area: SA2 - SA1 = 2lw + 2lh2 + 2wh2 - 2lw - 2lh1 - 2wh1 = 2l(h2 - h1).
So, the increase in surface area of the box is 2l(h2 - h1), where l represents the length of the box.
Second way to solve the problem:
Alternatively, we can calculate the increase in surface area by focusing on the change in the height only.
The two faces of the box that are affected by the increase in height are the top and bottom faces, each with an area equal to lw, and the two side faces, each with an area equal to lh1 and lh2.
Therefore, the increase in surface area of the box is equal to 2lw + 2lh2 - (2lw + 2lh1) = 2l(h2 - h1).
I prefer the second way of solving the problem because it directly focuses on the change in the height and eliminates the need to calculate the entire surface area of the box in both cases. It simplifies the calculation and reduces the chances of making errors. By isolating the change in the height, we can directly compute the increase in surface area, which is the desired result.
Learn more about surface area here: brainly.com/question/29298005
#SPJ11
- 1/2 + 3 1/2Mark answer in the grid. Use the correct place value.
Answers
According to the given data we have the following expression to solve:
- 1/2 + 3 1/2
To solve this expression we would have to make the following calculations:
First we would multiply 3 times 1/2
\(3\cdot\frac{1}{2}=\frac{3\cdot\:1}{1\cdot\:2}\)So, we would get:
\(-\frac{1}{2}+\frac{3}{2}\)\(\text{Next, }\mathrm{Apply\: the\: fraction\: rule}\colon\quad \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}\)\(So,\text{ }-\frac{1}{2}+\frac{3}{2}=\frac{-1+3}{2}\)\(\mathrm{Add\: the\: numbers\colon}\: -1+3=2\)So, Finally we would get the fraction 2/2 that would be equal to 1.
Therefore, - 1/2 + 3 1/2=1
sound travels at about 330 m/s in air How long would it take sound to travel 80 m.
Answers
330 m/s also means \(\dfrac{330 \text{ m}}{1 \text{ s}}\), which is the same as \(\dfrac{1 \text{ s}}{330 \text{ m}}\).
If you take that last version and multiply it by 80 m:
\(80 \text{ m} \cdot \dfrac{{1 \text{ s}}}{330 \text{ m}} = \dfrac{80}{330} \text{ s}\)
80/330 ≈ 0.2424...
five hamburgers cost 5.25 at this rate what is the cost of 8 hamburgers
Answers
Answer: 8.4
Step-by-step explanation: 5.25 divided by 5 is 1.05. So 1.05 x 8 is 8.4
2. Price of 1 is 1.05
3. 1.05 multiply by 8 is 8.40
ANSWER: $8.40 for 8
I need help with this please

Answers
The range of a function is the set of all possible output values (y-values) of the function. To find the range of f(x) = (5/2)^x - 5, we need to find the minimum and maximum values of y that can be obtained by plugging in all possible x values.
Since (5/2)^x is always greater than 0 for any x, the minimum value of f(x) is -5.To find the maximum value of f(x), we can take the limit as x approaches infinity:
lim (x → ∞) (5/2)^x - 5 = ∞ - 5 = ∞Therefore, the range of f(x) is (-5, ∞).A rubber gasket has a circumference of 3.2 cm. when placed in service, it expands by a scale factor of 2. what is the circumference of the gasket when in service?
a.
13.2 cm
b.
1.6 cm
c.
6.4 cm
d.
3.2 cm
Answers
6.4 cm is the needed circumference of the gasket following dilatation with a scale factor of 2.
What does circumference mean?
The boundary length of any circular shape is known as the
circumference.
What is scale factor?
A scale factor is a quantity multiplier (also known as a scale). The scaling factor for x, for instance, is represented by the letter "C" in the equation y = Cx. The factor would be 5 if y = 5x were the equation.
According to the given data:
After scale factor 2 is applied, 6.4 cm must be the gasket's needed circumference.
It includes a rubber gasket with a 3.2 cm circumference. The circumference of the gasket has must be calculated after scaling up by factor 2.
Here,
3.2 cm is the gasket's circumference.
The circumference changed upon scale factor 2 dilatation.
Dilated gasket circumference: 2 * 3.2 = 6.4 cm
As a result, 6.4 cm is the needed circumference of the gasket following dilatation with a scale factor of 2.
Learn more about scale factor at:
brainly.com/question/14769343
#SPJ4
Answer:
C. 6.4 cm
Hope this helps!
Step-by-step explanation:

Can someone help me with this?
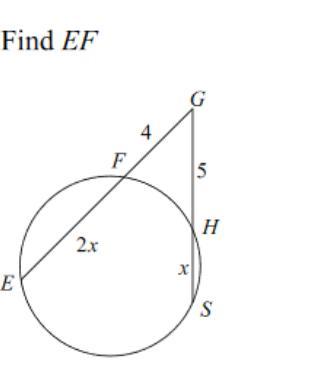
Answers
Answer:
E= 52 degrees and F=21 degrees
(sorry)
Step-by-step explanation:
Determine f(4) for A piecewise function f of x in three pieces. The function is defined by part 1, which is x cubed for x less than negative 3, part 2, which is 2 times x squared minus 9 for negative 3 is less than or equal to x which is less than or equal to 4, and part 3 which is 5 times x plus 4, for x greater than 4..
23
24
41
64
Answers
Answer:
23
Step-by-step explanation:
seen it before