Factor out the greatest common factor.
4x³+16x² +8x
Answers
The greatest common factor for 4x³+16x² +8x is 4x(x2- 4x - 2).
This solution focuses on simplification:
4x(x2-4x-2)
(4(x3)-24x2)-8x
(22x3-24x2) -8x
Take similar factors aside:
4x3-16x2-8= 4x(x2-4x-2)
Factoring x2 - 4x - 2
x2 is the initial term, and it has a coefficient of 1.
The coefficient of the intermediate term, which would be -4x, is 4.
"The constant," the final term, is -2.
Multiply the constant by the coefficient of the first term. 1 -2 = -2
The second step is to find two -2 factors whose sum is equal to the -4 coefficient of the middle word.
-2 + 1 = -1
-1 + 2 = 1
No two of these factors can be discovered!!
Trinomial cannot be factored.
Hence, The greatest common factor is 4x(x2- 4x - 2).
To learn more about greatest common factor, here;
brainly.com/question/11221202
#SPJ9
Related Questions
Classify each function as a power function, root function, polynomial (state its degree), rational function, algebraic function, trigonometric function, exponential function, or logarithmic function.
(a) y=Ï€x
(b) y=xπ
(c) y=x2(2−x3)
(d) y=tant−cost
(e) y=s1+s
(f) y=x3−1√1+x√3
Answers
(a) f(x) = \(log_2(x)\) is a logarithmic function
(b) g(x) = ∜x is a root function
(c) h(x) = \(2x^3/(1 - x^2)\) is a rational function
(d) u(t) = 1 - 1.1t + \(2.54t^2\) is a polynomial of degree 2
(e) v(t) = \(5^t\)is an exponential function
(f) w(θ) = sin θ \(cos^{2}\theta\) is a trigonometric function.
(a) f(x) = \(log_2(x)\) is a logarithmic function. Logarithmic functions have the logarithm of the independent variable as the output. Here, the logarithm base is 2.
(b) g(x) = ∜x is a root function. Root functions have the square root or higher roots of the independent variable as the output. Here, the root is a cube root.
(c) h(x) = \(2x^3/(1 - x^2)\) is a rational function. Rational functions are functions that are expressed as the quotient of two polynomials. Here, the numerator is a cubic polynomial and the denominator is a quadratic polynomial.
(d) u(t) = 1 - 1.1t + \(2.54t^2\) is a polynomial of degree 2. Polynomials are functions that are expressed as a sum of powers of the independent variable, with coefficients. The degree of a polynomial is the highest power of the independent variable.
(e) v(t) = \(5^t\) is an exponential function. Exponential functions have the independent variable as the exponent. Here, the base is 5.
(f) w(θ) = sin θ \(cos^{2}\theta\) is an algebraic function and a trigonometric function. Algebraic functions are functions that can be expressed using arithmetic operations and algebraic expressions. Trigonometric functions are functions that involve the ratios of the sides of a right triangle. Here, the function is a combination of sine and cosine functions.
Read more about functions:
brainly.com/question/28934802
#SPJ4
The complete question is -
Classify each function as a power function, root function, polynomial (state its degree), rational function, algebraic function, trigonometric function, exponential function, or logarithmic function.
(a) f(x) = \(log_2(x)\)
(b) g(x) = ∜x
(c) h(x) = \(2x^3/(1 - x^2)\)
(d) u(t) = 1 - 1.1t + \(2.54t^2\)
(e) v(t) = \(5^t\)
(f) w(θ) = sin θ \(cos^{2}\theta\)
I keep getting the wrong answer.

Answers
The volume of the solid obtained by rotating the region bounded by the curve y = 1 - (x - 5)² in the first quadrant about the y-axis is 51π cubic units.
What is the volume of the solid obtained by rotating the region in the first quadrant bounded by the given curve about the y - axis?To find the volume of the solid obtained by rotating the region bounded by the curve y = 1 - (x - 5)² in the first quadrant about the y-axis, we can use the method of cylindrical shells.
The formula for the volume using cylindrical shells is:
V = 2π ∫ [a, b] x * h(x) dx
Where:
- V is the volume of the solid
- π represents the mathematical constant pi
- [a, b] is the interval over which we are integrating
- x is the variable representing the x-axis
- h(x) is the height of the cylindrical shell at a given x-value
In this case, we need to solve for x in terms of y to express the equation in terms of y.
Rearranging the given equation:
x = 5 ± √(1 - y)
Since we are only interested in the region in the first quadrant, we take the positive square root:
x = 5 + √(1 - y)
Now we can rewrite the volume formula with respect to y:
V = 2π ∫ [c, d] x * h(y) dy
Where:
- [c, d] is the interval of y-values that correspond to the region in the first quadrant
To determine the interval [c, d], we set the equation equal to zero and solve for y:
1 - (x - 5)² = 0
Expanding and rearranging the equation:
(x - 5)² = 1
x - 5 = ±√1
x = 5 ± 1
Since we are only interested in the region in the first quadrant, we take the value x = 6:
x = 6
Now we can evaluate the integral to find the volume:
V = 2π ∫ [0, 1] x * h(y) dy
Where h(y) represents the height of the cylindrical shell at a given y-value.
Integrating the expression:
V = 2π ∫ [0, 1] (5 + √(1 - y)) * h(y) dy
To find h(y), we need to determine the distance between the y-axis and the curve at a given y-value. Since the curve is symmetric, h(y) is simply the x-coordinate at that point:
h(y) = 5 + √(1 - y)
Substituting this expression back into the integral:
V = 2π ∫ [0, 1] (5 + √(1 - y)) * (5 + √(1 - y)) dy
Now, we can evaluate this integral to find the volume
V = 2π ∫ [0, 1] (5 + √(1 - y)) * (5 + √(1 - y)) dy
To simplify the integral, let's expand the expression:
V = 2π ∫ [0, 1] (25 + 10√(1 - y) + 1 - y) dy
V = 2π ∫ [0, 1] (26 + 10√(1 - y) - y) dy
Now, let's integrate term by term:
\(V = 2\pi [26y + 10/3 * (1 - y)^\frac{3}{2} - 1/2 * y^2]\)] evaluated from 0 to 1
V = \(2\pi [(26 + 10/3 * (1 - 1)^\frac{3}{2} - 1/2 * 1^2) - (26 * 0 + 10/3 * (1 - 0)^\frac{3}{2} - 1/2 * 0^2)]\)
V = 2π [(26 + 0 - 1/2) - (0 + 10/3 - 0)]
V = 2π (25.5)
V = 51π cubic units
Learn more on volume of a solid obtained by rotating curve here;
https://brainly.com/question/32301706
#SPJ1
Calc II Question
Find the volume of the solid obtained by rotating the region bonded bt the given curves about the specified line.
Y = e^-x
Y = 1
X = 2
About the Y = 2
Answers
Answer:
\(\displaystyle \frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Step-by-step explanation:
This can be solved with either the washer (easier) or the shell method (harder). For the disk/washer method, the slice is perpendicular to the axis of revolution, whereas, for the shell method, the slice is parallel to the axis of revolution. I'll show how to do it with both:
Shell Method (Horizontal Axis)
\(\displaystyle V=2\pi\int^d_cr(y)h(y)\,dy\)
Radius: \(r(y)=2-y\) (distance from y=2 to x-axis)
Height: \(h(y)=2-(-\ln y)=2+\ln y\) (\(y=e^{-x}\) is the same as \(x=-\ln y\))
Bounds: \([c,d]=[e^{-2},1]\) (plugging x-bounds in gets you this)
Plugging in our integral, we get:
\(\displaystyle V=2\pi\int^1_{e^{-2}}(2-y)(2+\ln y)\,dy=\frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Washer Method (Parallel to x-axis)
\(\displaystyle V=\pi\int^b_a\biggr(R(x)^2-r(x)^2\biggr)\,dx\)
Outer Radius: \(R(x)=2-e^{-x}\) (distance between \(y=2\) and \(y=e^{-x}\))
Inner Radius: \(r(x)=2-1=1\) (distance between \(y=2\) and \(y=1\))
Bounds: \([a,b]=[0,2]\)
Plugging in our integral, we get:
\(\displaystyle V=\pi\int^2_0\biggr((2-e^{-x})^2-1^2\biggr)\,dx\\\\V=\pi\int^2_0\biggr((4-4e^{-x}+e^{-2x})-1\biggr)\,dx\\\\V=\pi\int^2_0(3-4e^{-x}+e^{-2x})\,dx\\\\V=\pi\biggr(3x+4e^{-x}-\frac{1}{2}e^{-2x}\biggr)\biggr|^2_0\\\\V=\pi\biggr[\biggr(3(2)+4e^{-2}-\frac{1}{2}e^{-2(2)}\biggr)-\biggr(3(0)+4e^{-0}-\frac{1}{2}e^{-2(0)}\biggr)\biggr]\\\\V=\pi\biggr[\biggr(6+4e^{-2}-\frac{1}{2}e^{-4}\biggr)-\biggr(4-\frac{1}{2}\biggr)\biggr]\)
\(\displaystyle V=\pi\biggr[\biggr(6+4e^{-2}-\frac{1}{2}e^{-4}\biggr)-\frac{7}{2}\biggr]\\\\V=\pi\biggr(\frac{5}{2}+4e^{-2}-\frac{1}{2}e^{-4}\biggr)\\\\V=\pi\biggr(\frac{5}{2}+\frac{4}{e^2}-\frac{1}{2e^4}\biggr)\\\\V=\pi\biggr(\frac{5e^4}{2e^4}+\frac{8e^2}{2e^4}-\frac{1}{2e^4}\biggr)\\\\V=\pi\biggr(\frac{5e^4+8e^2-1}{2e^4}\biggr)\\\\V=\frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Use your best judgment when deciding on what method you use when visualizing the solid, but I hope this helped!

You created a playlist, and 100 of your friends listened to it and shared if they
liked it or not. Mario said the ratio of the number of people who liked the playlist
to the number of people who did not like the playlist is 75:25. Lila said that for
every three people who liked the playlist, one person did not. Do they agree? *
Answers
Answer:
its yes
Step-by-step explanation:
A jar has 20 marbles: 3 green, 12 blue, 5 red.
What is the probability of randomly choosing a red and then a green marble (keep the red marble when you choose it)?
Answers
Probability is defined as the likelihood or the certainty that an event is going to occur or happen.
The probability of randomly choosing a red and then a green marble is \(3/76\).
The total number of marbles = 20
The number of green marbles= 3
The number of blue marbles = 12
The number of red marbles = 5
The probability of choosing a red marble = Number of red marbles / Total number of marbles
= 5/20
In simplest fraction form = \(\frac{1}{4}\)
We are told in the question that you keep the red marble you choose, So this means the total number of marbles left reduces to 19
The probability of choosing a green marble is = Number of green marbles / New total number of marbles
= 3/19
Therefore, the probability of randomly choosing a red and then a green marble is
P (Red) x P(Green)
= 1/4 x 3/19
= \(3/76\)
To learn more, visit the link below:
https://brainly.com/question/22563776
Use the procedures developed to find the general solution of the differential equation. (Let x be the independent variable.)
2y''' + 15y'' + 24y' + 11y= 0
Answers
Solution :
Given :
2y''' + 15y'' + 24y' + 11y= 0
Let x = independent variable
\((a_0D^n + a_1D^{n-1}+a_2D^{n-2} + ....+ a_n) y) = Q(x)\) is a differential equation.
If \(Q(x) \neq 0\)
It is non homogeneous then,
The general solution = complementary solution + particular integral
If Q(x) = 0
It is called the homogeneous then the general solution = complementary solution.
2y''' + 15y'' + 24y' + 11y= 0
\($(2D^3+15D^2+24D+11)y=0$\)
Auxiliary equation,
\($2m^3+15m^2+24m +11 = 0$\)
-1 | 2 15 24 11
| 0 -2 - 13 -11
2 13 11 0
∴ \(2m^2+13m+11=0\)
The roots are
\($=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$\)
\($=\frac{-13\pm \sqrt{13^2-4(11)(2)}}{2(2)}$\)
\($=\frac{-13\pm9}{4}$\)
\($=-5.5, -1$\)
So, \(m_1, m_2, m_3 = -1, -1, -5.5\)
Then the general solution is :
\($= (c_1+c_2 x)e^{-x} + c_3 \ e^{-5.5x}$\)
A variable needs to be eliminated to solve the system of equation below. Choose the correct first step.
3x-9y=-39. 3x-6y=-21
Answers
Answer:
3
−
9
=
−
3
9
3
−
6
=
-21
Step-by-step explanation:
3x−9y=−39, 3x−6y=−21 : x=5, y=6
Steps
[ 3x−9y=−39 3x−6y=−21 ]
Show Steps
Isolate x for 3x−9y=−39: x=−13+3y
Substitute x=−13+3y
[ 3(−13+3y)−6y=−21 ]
Show Steps
Simplify
[ −39+3y=−21 ]
Show Steps
Isolate y for −39+3y=−21: y=6
For x=−13+3y
Substitute y=6
x=−13+3· 6
Simplify
x=5
The solutions to the system of equations are:
I need help!! Please help me!! My question is attached, please show your work! There are two questions, answer both.

Answers
Answer:
Approximately 36.5885
Approximately 4.2426
Step-by-step explanation:
Please reference the drawing I've provided (sorry it's kind of awful. Drawing on a computer is hard :(
Problem 1)
So, the trapezoid can be split into a right triangle and a rectangle. To find the perimeter, we just need to find all the side lengths and add them.
We already know the dimensions of the rectangle. So, we need to find the dimensions of the right triangle.
We know that the height is 9 since it's opposite to the rectangle. Importantly, we know that the angle opposite to 9 is 60°.
This means that the other angle is 30°. So, the right triangle is a "special right triangle." In the 30-60-90 triangle, the hypotenuse is 2x, the side opposite to 60° is x√3, and the side opposite to 30° is x.
So, we know that 9 is the side opposite to 60°. Substitute and solve for x:
\(9=x\sqrt{3}\\ x=\frac{9}{\sqrt{3} } \\ x=\frac{9\sqrt3}{3}=3\sqrt3\)
So, x is 3√3. This means that the side opposite of angle 30 or d is 3√3.
And since x is 3√3, this means that the hypotenuse is 2(3√3) or 6√3.
Therefore, the perimeter of the figure would be:
\(9+6+6+3\sqrt3+6\sqrt3\\=21+9\sqrt3\\\approx36.5885\)
Problem 2:
For the bookcase, we simply need to find the value of c.
The braces that will be built is simply the hypotenuse of the right triangles. Therefore:
\(a^2+b^2=c^2\\\)
Plug in 3 for a and b:
\(3^2+3^2=c^2\\c^2=9+9=18\\c=\sqrt{18}=\sqrt{9\cdot 2}=3\sqrt2\approx4.2426\)
Therefore, each of the braces will be approximately 4.2426 feet long.
Edit: Grammar

Find the most general antiderivative of the function. (Use C for the constant of the antiderivative).
f(x) = 6x5 − 7x4 − 9x2
F(x) = ?
Answers
Answer:
\(x^6 - \frac{7x^5}{5} - 3x^3 + C\)
Find the length of wire required to fence it with three rounds. (i) If the rate of cost of fencing is Rs 25 per metre, find the total cost of fencing. b) Charimaya is running a race around a square track of length 75 m. Find the distance covered by her at the end of her fifth round. c) 540 m of wire is required to fence a square shaped of fish pond with three rounds. What is the length of wire required for one round? What is the perimeter of the pond? (ii) (iii) Find the length of the pond. Creative Section - B A rectangular ground is 25m long and 18m broad. (i) Find its perimeter. (ii) How many metres does a girl run around the ground when completes five rounds? b) Mrs. Kanchhi Tamang has a vegetable garden of length 30m and br 18m. (1) Find its perimeter. quired to fence it with 3 rounds.
Answers
The lengths and breadths of the rectangular shaped figures indicates;
a) i) Rs 6,900
b) 1500 m
c) (i) 180 m, (ii) 180 m, (iii) 45 m
Creative section B) (i) 86 meters, (ii) 430 meters
b) (i) 288 meters
What is a rectangle?A rectangle is a quadrilateral that has congruent facing sides and four interior right angles.
The possible part of the question includes;
The length of the fence = 27 meters
The breadth = 19 meters
The perimeter of the fencing = 2 × (27 + 19) = 92 meters
The length of three round of fencing = 3 × 92 meters = 276 meters
(i) The cost per meter = Rs 25
The total cost of fencing = Rs 25/m × 276 m = Rs 6,900
b) The length of the square track = 75 m
The distance at covered after the 5th round = 5 × 4 × 75 m = 1500 m
c) (i) The length of wire required for one round = 540 m/3 = 180 m
(ii) The perimeter of the pond = 180 m
(iii) The length of the pond = 180 m/4 = 45 m
Creative Section;
(i) The perimeter = 2 × (25 + 18) = 86 meters
(ii) The distance the girl runs after five rounds = 5 × 86 meters = 430 meters
b) i) The perimeter required to fence Mrs. Kanchhi's the vegetable garden with 3 rounds = 3 × 2 × (30 m + 18 m) = 288 m
Learn more on the perimeter of a rectangle here: https://brainly.com/question/29806262
#SPJ9
Pre - Calculus evaluate exponential derivative at a point !

Answers
Answer:
\(\displaystyle\)\(\displaystyle f'(1)=-\frac{9}{e^3}\)
Step-by-step explanation:
Use Quotient Rule to find f'(x)
\(\displaystyle f(x)=\frac{3x^2+2}{e^{3x}}\\\\f'(x)=\frac{e^{3x}(6x)-(3x^2+2)(3e^{3x})}{(e^{3x})^2}\\\\f'(x)=\frac{6xe^{3x}-(9x^2+6)(e^{3x})}{e^{6x}}\\\\f'(x)=\frac{6x-(9x^2+6)}{e^{3x}}\\\\f'(x)=\frac{-9x^2+6x-6}{e^{3x}}\)
Find f'(1) using f'(x)
\(\displaystyle f'(1)=\frac{-9(1)^2+6(1)-6}{e^{3(1)}}\\\\f'(1)=\frac{-9+6-6}{e^3}\\\\f'(1)=\frac{-9}{e^3}\)
Answer:
\(f'(1)=-\dfrac{9}{e^{3}}\)
Step-by-step explanation:
Given rational function:
\(f(x)=\dfrac{3x^2+2}{e^{3x}}\)
To find the value of f'(1), we first need to differentiate the rational function to find f'(x). To do this, we can use the quotient rule.
\(\boxed{\begin{minipage}{5.5 cm}\underline{Quotient Rule for Differentiation}\\\\If $f(x)=\dfrac{g(x)}{h(x)}$ then:\\\\\\$f'(x)=\dfrac{h(x) g'(x)-g(x)h'(x)}{(h(x))^2}$\\\end{minipage}}\)
\(\textsf{Let}\;g(x)=3x^2+2 \implies g'(x)=6x\)
\(\textsf{Let}\;h(x)=e^{3x} \implies h'(x)=3e^{3x}\)
Therefore:
\(f'(x)=\dfrac{e^{3x} \cdot 6x -(3x^2+2) \cdot 3e^{3x}}{\left(e^{3x}\right)^2}\)
\(f'(x)=\dfrac{6x -(3x^2+2) \cdot 3}{e^{3x}}\)
\(f'(x)=\dfrac{6x -9x^2-6}{e^{3x}}\)
To find f'(1), substitute x = 1 into f'(x):
\(f'(1)=\dfrac{6(1) -9(1)^2-6}{e^{3(1)}}\)
\(f'(1)=\dfrac{6 -9-6}{e^{3}}\)
\(f'(1)=-\dfrac{9}{e^{3}}\)
Tina pet sits to earn extra money. She charges a flat service fee of $20, plus $15 per day. If one of her customers spent less than $125, which of the following inequalities could be used to solve for x, the number of days the customer paid for pet sitting?
Answers
Therefore, **x < 7** is the inequality that may be utilized to find x
What is inequality?A mathematical statement known as an inequality compares two expressions using an inequality sign, such as (less than), > (greater than), or (less than or equal to).
For instance, the inequality x + 2 5 signifies that "x + 2 is less than 5".
Let x represent how many days the client paid for pet sitting.
$15 per day plus a $20 fixed service fee equals the total cost of pet sitting.
We are aware that the customer's purchase was under $125. Consequently, we can write:
20 + 15x < 125
Putting this disparity simply:
15x < 105
x < 7
To know more about inequality visit:
brainly.com/question/11536194
#SPJ1
What are the answers to these questions?

Answers
Step-by-step explanation:
the inside expression of an absolute value expression can be positive or negative, but the result is only the positive one.
therefore, for our example here the negative case would be
2.5x - 6.8 = -12.9
which gives us
2.5x = -6.1
x = -6.1/2.5 = -2.44
and the positive case would be
2.5x - 6.8 = 12.9
and that gives us
2.5x = 19.7
x = 19.7/2.5 = 7.88
Find the slope of a line perpendicular to the line whose equation is x + 6y = -24.
Fully simplify your answer.
Answers
Answer:
\(m_{perpendicular}\) = 6
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
given
x + 6y = - 24 ( subtract x from both sides )
6y = - x - 24 ( divide through by 6 )
y = - \(\frac{1}{6}\) x - 4 ← in slope- intercept form
with slope m = - \(\frac{1}{6}\)
given a line with slope m then the slope of a line perpendicular to it is
\(m_{perpendicular}\) = - \(\frac{1}{m}\) = - \(\frac{1}{-\frac{1}{6} }\) = 6
somebody pls help me !!! i’m close to a 90

Answers
Answer: the first sone should be it
Step-by-step explanation:
can someone help me with this (will give brainliest)
please view the attached image

Answers
Answer:
rate: 4 rate: -2
starting: 3 starting: 30
y= -4x + 3 y= -2x + 30
rate: 2 rate: 6
starting: -4 starting: 6
y= 2x -4 y= 6x + 6
Step-by-step explanation:
\(m = \frac{\text{rise}}{\text{run}} = \frac{y_2 - y_1}{x_2 - x_1}\)
^equation to find slope
To also find b, the starting value, you need to take any point given and substitute it back into the equation with the slope.
However, these problems give you the y-int already [it is the point like (0,y)]
7-3/1-0 = 4/1
rate: 4
starting: 3
y= 4x + 3
28-30/1-0= -2/1
rate: -2
starting: 30
y= -2x + 30
-2 - (-4)/1-0 = 2/1
rate: 2
starting: -4
y= 2x -4
6-0/1-0 = 6/1
rate: 6
starting: 6
y= 6x + 6
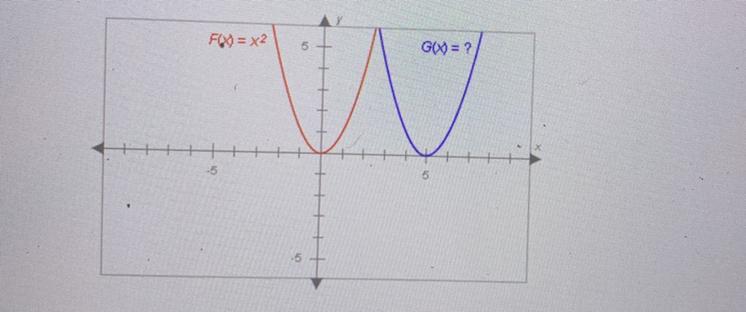
The graphs below have the same shape. Complete the equation of the blue
graph. Enter exponents using the caret (-); for example, enter x2 as x^2.
Answers
The answer : (x-5)^2 .....................................(x-5)square
For example, for f(x)= x square . For x=1 ,then, y=1 .
But consider the g function. the minimum value that g function has is x is 5. When x is 5, y is 0 . So (x-5)square is the equation of this function.
The complete equation of the blue graph is (x-5)^2.
What is a function?
Function is a type of relation, or rule, that maps one input to specific single output.
In mathematics, a function is an expression, rule, or law that describes the relationship between one variable (the independent variable) and another variable (the dependent variable) (the dependent variable). In mathematics and the physical sciences, functions are indispensable for formulating physical relationships.
Linear function is a function whose graph is a straight line
We are given that;
Red graph equation= X^2
Now,
In blue graph it shifted by 5 units to the right
For blue graph
x=5
Putting the value of x in red graph equation
=(x-5)^2
=x^2 + 25 - 10x
Therefore, by the given graph function will be (x-5)^2.
Learn more about function here:
https://brainly.com/question/2253924
#SPJ7
Write what the variable n represents in each expression.
L. Lisa can run the 100-yard dash 5 seconds faster than Jerry. Lisa's time is n-5
seconds.
M. Pedro is 3 times younger than his father. Pedro is n + 3 years old.
N. Lucia has $10.00 less than her sister. Lucia has n-10 dollars.
O. Jack is 2 times taller than his younger brother. Jack is 2 x n inches tall.
Answers
The variable n represents time in seconds
The variable n represents age
The variable n represents amount of money in dollars.
The variable n represents height in inches.
In each expression:
L. The variable n represents Jerry's time in seconds for the 100-yard dash. Lisa's time is n-5 seconds, indicating that Lisa runs 5 seconds faster than Jerry.
M. The variable n represents Pedro's father's age in years. Pedro's age is n + 3 years old, meaning Pedro is 3 years younger than his father.
N. The variable n represents Lucia's sister's amount of money in dollars. Lucia has n-10 dollars, indicating that Lucia has $10.00 less than her sister.
O. The variable n represents Jack's younger brother's height in inches. Jack is 2 times taller than his younger brother, so Jack's height is 2 times n inches.
Learn more about expression here:
https://brainly.com/question/28170201
#SPJ1
solve system by substitutition or elimination.
9x-8x=9
-18x+16y=-18
Answers
Answer:
1. 9x-8y=9
2. -18x+16y= -18 ⇒ -9x+8y= -9 ⇒ 9x-8y=9
as we see both equations are same, it means the lines overlap and there is infinite number of solutions
Enter the number that belong in the green box please help

Answers
Step-by-step explanation:
Since we have three sides and trying to find an angle, use Law of Cosines
\(c = \sqrt{ {a}^{2} + {b}^{2} - 2ab \times \cos(d) } \)
where c is
Solving for the angle d.
\( \cos {}^{ -1 } (( \frac{ {c}^{2} - {b}^{2} - {a}^{2} }{ - 2ab} ) = d\)
where d is in degrees
The angle d is the opposite of the side c.
It does not matter what a and b is(they can be either 4 or 5)
let
c=7
a=4
b=5
\( \cos {}^{ - 1} ( \frac{ - 1}{5} ) = d\)
This angle must be within 0 and 180
We get
\(d = 101.54\)
6 to the 3rd power ÷ 4 + 2 x 9(32 x 8 – 17 x 4).
HELP
Answers
Answer:
6 to the 3rd power ÷ 4 + 2 ×9(256-17×4)
6 to the 3rd power ÷ 4 + 2 ×9(256-68)
6 to the 3rd power ÷ 4 + 2 ×9×188
216 ÷ 4 + 2 × 1692
216 ÷ 4 + 3384
54 + 3384
=3438
Which graph represents y as a function of x?

Answers
===========================================================
Reason:
This graph passes the vertical line test, so it is a function.
The vertical line test is where we try to pass a single vertical line through more than one point on the curve. If such a thing is possible, then we say the curve fails the vertical line test and it's not a function.
Graph D for instance can have a vertical line through x = 1 and intersect the curve at (1,4) and (1,-4) simultaneously. The input x = 1 leads to multiple outputs (y = 4 and y = -4). Graph D fails the vertical line test for this very reason, and it is not a function. Graphs A and B are similar stories. Any vertical line itself is automatically not a function.
To have a function, any x input in the domain must lead to exactly one and only one y output in the range.
---------
Notice with graph C it is impossible to have a single vertical line intersect more than one point on the curve. So this is why graph C passes the vertical line test. Each input leads to exactly one output.
$46.76 for 4 pounds. What is the price per pound?
Answers
9514 1404 393
Answer:
$11.69 per pound
Step-by-step explanation:
To find price per pound, divide price by pounds:
$46.76/(4 lb) = $11.69/lb
Alijah had a taxable income of $8450 and filed his federal income tax return with the Single filing status. Using the table below, find the amount he has to pay in taxes.
Single
Taxable income is over
8.350
33 950
82.750
171.550
372,950
But nat over
8,350
33.950
82,250
171.550
372.550
The tax is
Plus
50.00
835.00
4 675.00
16.750.00
41,754.00
108,216.00
10%
15%
25%
20%
33%
35%
Of the
amount over
50
8.350
33.950
82,250
171.550
372,850
O A. $835.00
• B. $850.00
O c. $2087.50
O D. $1252.50
Answers
Answer:
Step-by-step explanation:
67
Alijah's taxable income puts him in the first tax bracket, over $8,350 but not surpassing $33,950. Hence, his tax due is a base of $835 plus 15% of the income that exceeds $8,350. This results in a total tax payable of $850. Option B is the correct answer.
Alijah's taxable income falls within the first bracket of the tax table given, being over $8,350 but not over $33,950.
This bracket requires him to pay a tax of $835.00 plus 15% of the amount over $8,350.
He has a surplus of $100 over the $8,350 threshold (i.e., $8,450 - $8,350), and 15% of $100 equals $15.
Therefore, the total tax he owes would be the fixed amount of $835.00 plus the $15.00 calculated, which sums up to $850.00.
Thus, looking at the provided options, option B ($850.00) would be the correct answer.
Learn more about Income Tax here:
https://brainly.com/question/34135935
#SPJ2
A box without a top is to be made from a rectangular piece of cardboard, which has a length of 30 in by 10 in, by cutting out squares with side lengths, x, from each corner. > Determine the value of x that will maximize the volume of the box. Round your answer to the nearest tenth.
Answers
Cutting squares with side length approximately 3.8 inches from each corner will result in a box with the maximum volume.
What is the value of x that will maximize the volume of the box?To determine the value of x that will maximize the volume of the box, we can start by visualizing the box and expressing its volume in terms of x.
When we cut out squares with side lengths x from each corner of the rectangular cardboard, the resulting shape, when folded, will form the box without a top. The height of the box will be equal to the side length of the squares, which is x. The length and width of the base of the box will be the dimensions of the cardboard after the squares are cut out, which will be (30 - 2x) and (10 - 2x) respectively.
The volume of the box can be calculated by multiplying the dimensions of the base and the height:
V(x) = (30 - 2x)(10 - 2x)x.
To find the value of x that maximizes the volume, we can take the derivative of V(x) with respect to x, set it equal to zero, and solve for x.
dV/dx = 0.
Let's calculate the derivative of V(x):
dV/dx = [(30 - 2x)(10 - 2x)]'x + (30 - 2x)(10 - 2x) * 1.
Simplifying and setting it equal to zero:
[(30 - 2x)(10 - 2x)]'x + (30 - 2x)(10 - 2x) = 0.
Solving for this;
x = 3.8 inches
Learn more on maximizing volume of square here;
https://brainly.com/question/30351524
#SPJ1
2+2=
a. 3
b. 5
c. 4
d. 7
Answers
Answer:
C
Step-by-step explanation:
2
+2
-----
4
2) A 25 foot ladder leans against a house. The base of the ladder is 7 feet
away from the house. What is h, the height of the house? #2 pleasee

Answers
Step by step
Using Pythagorean theorem, we can find the height of the right triangle
We know a= 7, we know c= 25, we need to find b
a^2 + b^2 = c^2
7^2 + b^2 = 25^2
49 + b^2 = 625
Subtract 49 from both sides to solve b
49 - 49 + b^2 = 625 - 49
b^2 = 576
Take square root of both sides
√ b^2 = √ 576
b = 24 ft
Now according to the drawing, the ladder did not go to the top of the house, we need to add 11 ft to 24 ft = 35 ft total height
Evaluate the following expression when x = -5 and y = 25.
A. -3,130
B. -630
C. 3,120
D. 620
Answers
Plzzzzz helpppp, Find the value of x

Answers
Answer:
51
Step-by-step explanation:
Select the solution to the following system of equations:

Answers
Answer:
4x+2y=4
3x-y=-7
first one by 3
second by 4
12x+6y=12
12x-4y=-28
subtract
10y=40
y=4
plug in
3x-4=-7
add 4
3x=-3
x=-1
(-1,4)
c
Hope This Helps!!!
Answer: third option
Step-by-step explanation:
There are 2 ways to go about systems of equations normally, and that's elimination and substitution. For this particular problem, I would recommend elimination.
we see the first equation 4x+2y=4
we want to be able to simplify it as much as possible (so it's easier to solve)
so we divide all the terms by 2, giving 2x+y=2.
the second equation can't be simplified, so we set up the elimination method.
2x+y=2
-3x-y=-7
multiplying both equations by 2 and 3, we subtract them and get that y equals 4, which is clearly the answer.