Factor and SHOW ALL STEPS: 2x3+10x2+12x
Please need it fast. Please and thank you.
Answers
Answer:
2x(x + 2)(x + 3).
Step-by-step explanation:
2x3+10x2+12x
The GCF is 2x so
= 2x(x^2 + 5x + 6)
= 2x(x + 2)(x + 3).
Related Questions
Consider your construction of pentagon ABCED.
What segments, if any, are parallel? Explain how you made your
determination.

Answers
Therefore , the solution of the given problem of pentagonal comes out to be Nadia has created a pentagonal prism as a result.
Define pentagonal.Pentagons are two-dimensional polygons having five sides and fifth angles. When we mix the Greek terms "penta" and "gon," which mean "five" and "angles," respectively, we have the word "pentagon."
Here,
we know that a pentagonal prism has five rectangular sides in addition to two pentagonal bases at the top and bottom.
Pentagonal prisms are pentagon-shaped if we look at them from the bottom.
When viewed from the side, a pentagonal prism would have a rectangular shape.
If we were to look at the pentagonal prism from the front, it would appear rectangular.
Therefore , the solution of the given problem of pentagonal comes out to be Nadia has created a pentagonal prism as a result.
To learn more about the pentagonal visit:
brainly.com/question/26709266
#SPJ1
A box contains 10 transistors, 3 of which are defective. If 3 are selected at random, find the probability of the statements below. a. All are defective b. None are defective Answers has to be a fraction
Answers
Answer:
1. 1/120
2. 7/24
Step-by-step explanation:
n = 10
Number of defective = 3
1. Probability of all defective =
(Number of defective/n) x (number of defective -1/n -1)...(number of defective -n/n-1)
=3/10 x 2/9 X 1/8
= 6/720
= 1/120
2. probability of none defective
Since 3 are defective, those that are not defective = 7
The probability is therefore:
7/10 x 6/9 x 5/8
= 210/720
= 7/24.
a company's marginal cost function is 8 √ x where x is the number of units. find the total cost of the first 64 units (of increasing production from x=0 to x=64)
Answers
Thus, the total cost of the first 64 units is approximately $2730.67.
To find the total cost of the first 64 units, we need to integrate the marginal cost function over the range of production from x=0 to x=64.
The marginal cost function is given by C'(x) = 8√x.
Integrating this function with respect to x, we get:
C(x) = ∫(8√x dx) = 8 * (2/3)x^(3/2) + C
To find the total cost for the first 64 units, we need to evaluate C(x) at x=64 and x=0 and subtract the results:
C(64) - C(0) = (8 * (2/3) * 64^(3/2) + C) - (8 * (2/3) * 0^(3/2) + C)
Simplifying the equation, we get:
C(64) - C(0) = 8 * (2/3) * 64^(3/2)
Now, compute the value:
C(64) - C(0) = 8 * (2/3) * 512 = (16/3) * 512 ≈ 2730.67
So, the total cost of the first 64 units is approximately $2730.67.
Know more about the marginal cost function
https://brainly.com/question/17481520
#SPJ11
help me pls in math plssss

Answers
Answer:
The answer is of this question is 324.
Which best describes the structure outlined in the
bridge.
O It is a parallelogram because it has one pair of
opposite sides that is parallel.
O It is a parallelogram because it has exactly one pair
of opposite sides that is congruent.
It is a trapezoid because it has exactly one pair of
opposite sides that is congruent.
It is a trapezoid because it has exactly one pair of
opposite sides that is parallel.
Answers
It is a trapezium because there is only one set of parallel opposite edges.
Which best describes the parallelogram's sides?A parallelogram is a quadrilateral with two pairs of parallel edges. In a parallelogram, the opposing edges are of equal length, and the opposing angles are of equal size. Additionally, the internal angles that are supplementary to the transversal on the same side.
Which of the following statements about parallelograms is untrue?The diagonals of a parallelogram must cross one another in order for it to exist. do. As a result, we can conclude that only the third assertion is false, making option (C) Diagonals cut in half opposing lines.
To know more about trapezium visit:-
https://brainly.com/question/22607187
#SPJ9
Chris rented a truck for one day. There was a base fee of $15.99 , and there was an additional charge of 77 cents for each mile driven. Chris had to pay $234.67 when he returned the truck. For how many miles did he drive the truck?
Answers
Answer:
Chris drove the truck for 284 miles.
Step-by-step explanation:
Let us assume the total number of miles driven by Chris be \(x\). Now, as per the question, we can say that the sum of the base fee and the additional charge for each mile will be equal to the total rent that Chris will have to pay when he returns the truck. Next, we know that 1 cent = \(1/100\) $. So, we have,
77 cents = 0.77 $
So, we can say that,
⇒\(15.99+0.77x=234.67\)
⇒\(0.77x=234.67-15.99\)
⇒\(0.77x=218.68\)
⇒\(x=218.68/0.77\)
⇒\(x=284\)
Hence, Chris drove for a total of 284 miles when he returned the truck.
A bag contains two yellow, two blue, and four red marbles. How many blue marbles must be added to the bag to make the probability of drawing a blue marble 1/2
Answers
We need to add 4 blue marbles to the bag to make the probability of drawing a blue marble 1/2.
Currently, there are two blue marbles out of a total of eight marbles in the bag, so the probability of drawing a blue marble is 2/8 or 1/4.
Let x be the number of blue marbles we need to add to the bag. After adding x blue marbles, there will be a total of 2 + x blue marbles in the bag, out of a total of 8 + x marbles.
We want the probability of drawing a blue marble to be 1/2, so we can set up the equation:
(2 + x) / (8 + x) = 1/2
Multiplying both sides by (8 + x), we get:
2 + x = (8 + x) / 2
Multiplying both sides by 2, we get:
4 + 2x = 8 + x
Subtracting x from both sides, we get:
4 + x = 8
Subtracting 4 from both sides, we get:
x = 4
Therefore, we need to add 4 blue marbles to the bag to make the probability of drawing a blue marble 1/2.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
. Find the characteristic equation and the eigenvalues (and a basis for each of the corresponding eigenspaces) of the matrix. 12 - 3 -4 (a) the characteristic equation (b) the eigenvalues (Enter your answers from smallest to largest.) (11, 12) = a basis for each of the corresponding eigenspaces X1 = X2 =
Answers
The characteristic equation of the matrix is: λ² - 23λ + 132 = 0 and the eigenvalues of the matrix are λ = 11, and λ = 12 and A basis for the corresponding eigenspace for λ = 11 is X₁ = { (3y, y) | y ∈ ℝ }.A basis for the corresponding eigenspace for λ = 12 is X₂ = { (-y, y) | y ∈ ℝ }
The given matrix is:
| 12 -3 |
| -4 11 |
(a) The characteristic equation is found by setting the determinant of the matrix subtracted by the identity matrix equal to zero:
| 12 - λ -3 |
| -4 11 - λ | = 0
Expanding the determinant, we have:
(12 - λ)(11 - λ) - (-3)(-4) = 0
(132 - 12λ - 11λ + λ²) + 12 = 0
λ² - 23λ + 120 + 12 = 0
λ² - 23λ + 132 = 0
(b) To find the eigenvalues, we solve the characteristic equation for λ. Factoring the equation, we have:
(λ - 11)(λ - 12) = 0
Setting each factor equal to zero, we find the eigenvalues:
λ - 11 = 0 => λ = 11
λ - 12 = 0 => λ = 12
So the eigenvalues are 11 and 12.
To find the basis for each eigenspace, we need to solve the equation (A - λI)v = 0 for each eigenvalue, where A is the given matrix, λ is the eigenvalue, and v is the eigenvector.
For λ = 11:
(A - 11I)v = 0
Substituting the values, we have:
| 12 - 11 -3 | | x | | 0 |
| -4 11 - 11 | × | y | = | 0 |
Simplifying, we get the equations:
x - 3y = 0 => x = 3y
Therefore, a basis for the eigenspace corresponding to λ = 11 is:
X₁ = { (3y, y) | y ∈ ℝ }
For λ = 12:
(A - 12I)v = 0
Substituting the values, we have:
| 12 - 12 -3 | | x | | 0 |
| -4 11 - 12 | × | y | = | 0 |
Simplifying, we get the equations:
-3x - 3y = 0 => x + y = 0 => x = -y
Therefore, a basis for the eigenspace corresponding to λ = 12 is:
X₂ = { (-y, y) | y ∈ ℝ }
To summarize:
(a) The characteristic equation is λ² - 23λ + 132 = 0.
(b) The eigenvalues are 11 and 12.
A basis for the corresponding eigenspace for λ = 11 is X₁ = { (3y, y) | y ∈ ℝ }.
A basis for the corresponding eigenspace for λ = 12 is X₂ = { (-y, y) | y ∈ ℝ }
you can learn more about Matrix at: brainly.com/question/28180105
#SPJ11
Use long division to divide.
691 ÷ 9
Answers
Answer ⇒
= 76
Step - By - Step Explanation ⇒
It is not easy to write long division on a laptop as it paper, so I have attached an image from a calculator that I found online.

What is the range of this function?OA. (3, 5, 7, 11)OB. (-3, 4, 5, 7)OC. (-3, 0, 3, 4, 5, 6, 7,)OD. (-3, 0, 4, 6)

Answers
SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Define the range of a function
The range of a function is the set of its possible output values. The range of a function refers to the entire set of all possible output values of the dependent variable
STEP 2: Get the range of the function
The range of the function will be:
\(\lbrace-3,0,4,6\rbrace\)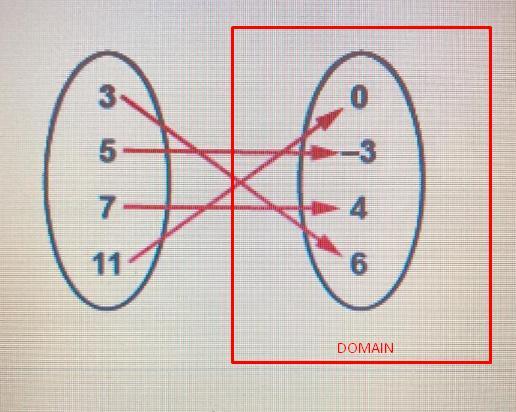
HELP ME ILL GIVE YALL BRAINLIESST

Answers
Answer:
615.44 cm^2
Step-by-step explanation:
here r, radius is 14 cm and π as 3.14
area of circle = π\(r^{2}\)
3.14 * 14^2
3.14 * 14 * 14
615.44cm^2
Answer:
The area of the hubcap is about \(\boxed{\tt{615.44}}\) cm².
Step-by-step explanation:
Solution :Here's the required formula to find the area of hubcap :
\(\longrightarrow{\pmb{\sf{Area_{(Circle)} = \pi{r}^{2}}}}\)
➝ π = 3.14 ➝ r = radiusSubstituting all the given values in the formula to find the area of hubcap :
\(\longrightarrow{\sf{Area_{(Hubcap)} = \pi{r}^{2}}}\)
\(\longrightarrow{\sf{Area_{(Hubcap)} = 3.14{(14)}^{2}}}\)
\(\longrightarrow{\sf{Area_{(Hubcap)} = 3.14{(14 \times 14)}}}\)
\(\longrightarrow{\sf{Area_{(Hubcap)} = 3.14{(196)}}}\)
\(\longrightarrow{\sf{Area_{(Hubcap)} = 3.14 \times 196}}\)
\(\longrightarrow{\sf{Area_{(Hubcap)} = 615.44}}\)
\(\star{\underline{\boxed{\sf{\purple{Area_{(Hubcap)} = 615.44 \: {cm}^{2}}}}}} \)
Hence, the area of hubcap is 615.44 cm².
\(\rule{300}{2.5}\)
(a+b)^2hiiiiiiiiiiiiii
Answers
Answer:
a^2+2ab+b^2 is the formula
Question
Name the included angle between JK¯¯¯¯¯¯¯¯
and KL¯¯¯¯¯¯¯¯
.
Answers
Answer:
K is the angle between JK and KL. It is called the included angle of sides JK and KL.
please help find the correct solutions for the equations below 2x+20=-3x-25 x= -7x+14=4x- 19 x= 10x-3=-5x-18 x= answers 8 5 6 24 -1 -9 20 3 10 -2
Answers
Answer:
I think its 8
Step-by-step explanation:
3(x+6)+6x+9=7x+8 Solve for x.*
A -19/2
B 19/2
C 2/19
D -2/19
Answers
Answer:
a) -19/2
Step-by-step explanation:
3(x+6)+6x+9=7x+8
3x + 18 + 6x + 9 = 7x + 8
3x + 6x - 7x = 8 - 18 - 9
2x = -19
2x/2 = -19/2
Therefore, x = -19/2
a candy distributor needs to mix a 10% fat-content chocolate with a 50% fat-content chocolate to create 100 kilograms of a 14% fat-content chocolate. how many kilograms of each kind of chocolate must they use?
Answers
The candy distributor needs to use 30 kilograms of 10% fat-content chocolate and 70 kilograms of 50% fat-content chocolate to create 100 kilograms of a 14% fat-content chocolate.
To solve this problem, we can use the method of mixture problems, which involves setting up a system of equations. Let x be the number of kilograms of the 10% fat-content chocolate and y be the number of kilograms of the 50% fat-content chocolate.
We have two equations based on the fat content and the total weight of the mixture:
0.1x + 0.5y = 0.14(100) (equation for fat content)
x + y = 100 (equation for total weight)
We can solve this system of equations using substitution or elimination. Using substitution, we can solve for x in terms of y from the second equation and substitute it into the first equation:
x = 100 - y
0.1(100 - y) + 0.5y = 0.14(100)
10 - 0.1y + 0.5y = 14
0.4y = 4
y = 10
Then we can substitute y = 10 back into the equation for x and get:
x = 100 - y = 100 - 10 = 90
To know more about elimination, refer here:
https://brainly.com/question/14619835#
#SPJ11
The probability that Cody will be first in the 50m backstroke Is 25%. What are the odds In favour of him being first?
Answers
Answer:
To find the odds in favor of Cody being first, we need to divide the probability of him winning (25%) by the probability of him not winning (75%).
Odds in favor of Cody winning = 25% / (100% - 25%) = 25% / 75%
Simplifying, we get:
Odds in favor of Cody winning = 1/3
Therefore, the odds in favor of Cody being first in the 50m backstroke are 1 to 2 (or 1:2).
Solve the equation: 3/8g + 2 = 5
Answers
Answer:
3/8g + 2 = 5
Subtract the number 2 from both sides of the equation.
3/8g = 3
Now divide 3/8 from both sides of the equation.
3/8 divided by 3/8 equals 0. 3 divided by 3/8 equals 8.
The final answer is:
g = 8
------------------------------------------------------------------------------------------
Check your answer:
3/8g + 2 = 5
Substitute 8 into the spot where the variable g was.
3/8 X 8 + 2 = 5
So our answer x = 8 is true.
Step-by-step explanation:
I hope that this has helped you to understand this equation. If you have any questions please put them below in the comments. If there are no questions, please have a great rest of your day/night!
Suppose an insurance company wants to determine the average speed of cars passing through an intersection. They randomly selected 85 cars and found their average speed to be 42 miles per hour with standard deviation of 4.2 miles per hour. A 90% confidence interval for the average speed of all the cars passing through the intersection is
Answers
The 90% confidence interval for the average speed of all the cars passing through the intersection is (41.29, 42.71) miles per hour.
To calculate the confidence interval, we can use the formula:
Confidence interval = Sample mean ± (Critical value * Standard error)
Given that the sample mean is 42 miles per hour and the standard deviation is 4.2 miles per hour, we need to determine the critical value and the standard error.
Since we have a sample size of 85, we can use the t-distribution with (n-1) degrees of freedom to find the critical value. With a 90% confidence level, the corresponding critical value for a two-tailed test is approximately 1.66.
The standard error is calculated as the standard deviation divided by the square root of the sample size:
Standard error = (Standard deviation) / √(Sample size)
Standard error = 4.2 / √85 ≈ 0.456
Now we can plug in the values into the confidence interval formula:
Confidence interval = 42 ± (1.66 * 0.456)
Confidence interval ≈ (41.29, 42.71)
Therefore, the 90% confidence interval for the average speed of all the cars passing through the intersection is (41.29, 42.71) miles per hour.
Based on the given data and calculations, we can conclude that with 90% confidence, the average speed of all the cars passing through the intersection falls within the range of 41.29 to 42.71 miles per hour.
To know more about intersection , visit :
https://brainly.com/question/12089275
#SPJ11
Last month, Korey’s Comics had a gross profit of $4,370 and a net income of $3,500. Calculate Korey’s operating expenses for last month.
a.
$787
b.
$870
c.
$7,870
d.
$8,700
Answers
Answer: B. $870
Step-by-step explanation:
Correct on Edge2021
Korey’s operating expenses for last month would be $870
What is the gross profit margin?The gross profit margin is a profitability raio. Profitability ratios measures the efficiency with which a company generates profit from its asset. Gross profit margin measures the return on sales.
Gross profit margin can be calculated by dividing the gross profit (difference between revenue and cost of goods sold) by revenue (Net sales). It could be expressed as a percentage by multiplying by 100.
Therefore, Gross profit margin = (gross profit ÷ net sales) x 100
Gross profit = $3,320
Net sales = $4,350
Gross profit margin = ($3,320÷$4,350) * 100
0.763 * 100 = 76.3%
4,350 - 3,320 = 1030
That would be 870 dollar.
To learn more about profit margin, please check: brainly.com/question/26208770
#SPJ7
At what value(s) of x does fx) x4-18x2 have a critical point where the graph changes from decreasing to increasing? (4 points) 0 and -3 only 0 and 3 only 0 -3, and 3 only 0 only DELL
Answers
The correct answer is: 0, -3, and 3. At 0, -3, and 3 of x does fx) x4-18x2 have a critical point where the graph changes from decreasing to increasing.
To find the critical points where the graph of the function f(x) = x^4 - 18x^2 changes from decreasing to increasing, we need to find the values of x where the derivative of the function is equal to zero or does not exist.
Let's find the derivative of f(x) with respect to x:
f'(x) = 4x^3 - 36x
To find the critical points, we set the derivative equal to zero and solve for x:
4x^3 - 36x = 0
Factor out 4x:
4x(x^2 - 9) = 0
Now we have two factors:
1) 4x = 0, which gives x = 0
2) x^2 - 9 = 0, which gives x = ±3
So, the critical points where the graph changes from decreasing to increasing are x = 0, x = -3, and x = 3.
Therefore, the correct answer is: 0, -3, and 3.
Visit here to learn more about graph brainly.com/question/17267403
#SPJ11
Faizah is paid $11 per hour for her work at a factory. She works 9 hours a day and 24 days a month. She saves $594 a month. Express the amount she saves as a percentage of her income.
Answers
Answer:
The amount she saves is 25% of her income
Step-by-step explanation:
She is paid $11 per hour
She works 9 hours per day
and for 24 days per month
So, she works 9(24) hours per month
= 216 hours per month
Now, she is paid $11 hourly, so for 216 hours,
she will have 11(216) = $2376
Total income = $2376 per month
Saving = $594 per month
As a percentage, we divide the savings by the total income,
savings/(total income) = 594/2376 = 1/4 = 0.25
Hence we get 25%
The volume of a cuboid is 594cm3. The length is 9cm and the width is 60mm. Work out the height of the cuboid in cm
Answers
The height of the cuboid is 2.33 cm. To determine the height of a cuboid whose volume is 594cm³, with a length of 9 cm and a width of 60 mm, it is important to first convert the width into cm.
This can be done by dividing it by 10, since 1 cm = 10 mm. Therefore, the width is 6 cm. Thus, the formula for the volume of a cuboid is V = lwh, where l = length, w = width, and h = height.
Therefore, substituting the known values into the formula, we get: 594 = 9 × 6 × h
Dividing both sides by 54, we get: h = 2.33 (rounded off to two decimal places).
Therefore, the height of the cuboid is 2.33 cm.
For more question on cuboid
https://brainly.com/question/26403859
#SPJ8
Al saves pennies. He agreed to give six thirteenths of his pennies to Bev if she would give six thirteenths of what she got from Al to Carl and if Carl in turn would give six thirteenths of what he got from Bev to Dani. Bev, Carl, and Dani agreed and Dani received 2376 pennies. How many pennies did Al have initially?
Answers
Answer:
Step-by-step explanation:
Let x represent the number of pennies that Al had initially.
He agreed to give six thirteenths of his pennies to Bev. It means that the number of pennies that he gave to Bev is 6/13 × x = 6x/13
if she would give six thirteenths of what she got from Al to Carl, it means that the number of pennies that Carl received is 6/13 × 6x/13 = 36x/169
if Carl in turn would give six thirteenths of what he got from Bev to Dani and Dani received 2376 pennies, it means that
6/13 × 36x/169 = 2376
216x/2179 = 2376
216x = 2376 × 2179
216x = 5220072
x = 5220072/216
x = 24167
AI had 24167 pennies initially
The length of the base edge of a square pyramid is 6 ft, and the height of the pyramid is 16 ft. What is the volume of the pyramid? 96 ft3 192 ft3 288 ft3 576 ft3
Answers
The volume of the pyramid is B) 192ft
The volume of a pyramid can be calculated utilizing the condition:
V = (1/3) * base region * height...........(1)
In the case of a square pyramid, the base area is given by the condition:
base area = (edge length)²
Thus, in this issue, we have:
base area = (6 ft)² = 36 ft²
height = 16 ft (given)
Substituting these values into the condition for the volume of a pyramid ( equation (1) ), we get:
V = (1/3) * 36 ft² * 16 ft
V = 192 cubic feet
In this way, the volume of the pyramid is 192 cubic feet.
To know more about the volume of the pyramid refer to this:
https://brainly.com/question/18994842
#SPJ4
Awad claims that when m is a negative integer and n is a positive integer, n - m is
always negative. Is Awad's claim true or false? Explain your reasoning. If it is true,
give an example to support his claim. If it is false, give a counterexample. Explain
your reasoning.
Answers
Using the concept of integer it can be concluded that Awad's claim is false.
What is an integer ?Integer, a positive, negative, or 0 with a complete value. The counting numbers 1, 2, 3, and so forth are used to create the integers, together with the subtraction process. A counting number can be divided by itself and the result is always zero; for instance, 4 divided by 4 equals 0. The result of subtracting a larger number from a smaller one is a negative whole number; for instance, 2 - 3 = 1. By deriving each integer in this way from the counting numbers, a set of numbers that can be closed with the subtraction operation is produced.
You can have positive or negative numbers. Negative numbers are frequently surrounded by brackets to make them simpler to read, for example (-2). Positive numbers typically don't have the + before the number. 3 is actually +3. Positive and negative number combinations can be confusing to add and multiply, thus caution is advised.
Subtraction and Addition
Two "pluses" equal a "plus," and two "minuses" equal a "plus." A negative is made up of a plus and a minus.
Whenever you subtract a negative number, you always end up adding because two negatives make a positive. For example,
n = 4
m = -3
then,
4-(-3) is going to turn into 4+3 = 7.
To know more about integers, visit :
https://brainly.com/question/15276410
#SPJ9
How is the series 3+5+7+...+51 represented in sigma notation?

Answers
Answer:
The third one
Step-by-step explanation:
The only one which gives the last number of the sequence is the third one as subbing in 16 you get 3×16 + 3 = 48 + 3 = 51
Find the standard form of the equation of the parabola with the given characteristics.
Vertex: (-5, 4); directrix: x = -12
Answers
Check the picture below, so the parabola looks more or less like so, with a "p" distance of positive 7.
\(\textit{horizontal parabola vertex form with focus point distance} \\\\ 4p(x- h)=(y- k)^2 \qquad \begin{cases} \stackrel{vertex}{(h,k)}\qquad \stackrel{focus~point}{(h+p,k)}\qquad \stackrel{directrix}{x=h-p}\\\\ p=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix}\\\\ \stackrel{p~is~negative}{op ens~\supset}\qquad \stackrel{p~is~positive}{op ens~\subset} \end{cases} \\\\[-0.35em] ~\dotfill\)
\(\begin{cases} h=-5\\ k=4\\ p=7 \end{cases}\implies 4(7)(~~x-(-5)~~) = (~~y-4~~)^2 \implies 28(x+5)=(y-4)^2 \\\\\\ x+5=\cfrac{1}{28}(y-4)^2\implies \boxed{x=\cfrac{1}{28}(y-4)^2 - 5}\)

WILL GIVE BRAINIEST!!!

Answers
The quadratic regression equation that best fits the data is:
y = 32.86x² - 379.14x + 1229.14.
How to obtain the regression equation?Regression equations are obtained inserting the points of a table or of a scatter plot into a calculator.
The choice of calculator is relevant to the type of regression equation desired. For this problem, it is stated that a quadratic regression equation is desired, hence the calculator used is for quadratic regression.
From the table given on the right side of the image, the points that will be used to build the quadratic regression equation are given by the ordered pairs presented as follows:
(3, 330), (4, 276), (5, 263), (6, 86), (7, 174), (8, 198), (9, 553).
Inserting these points into a calculator, the quadratic regression equation that best fits the data from the table is given below:
y = 32.86x² - 379.14x + 1229.14.
The concave up parabola is expected, as the measures in the table start decreasing and after the vertex they increase.
A similar problem, also featuring regression equations, is presented at https://brainly.com/question/29613968
#SPJ1
At a local restaurant, the amount of time that customers have to wait for their food is
normally distributed with a mean of 32 minutes and a standard deviation of 3
minutes. Using the empirical rule, determine the interval of minutes that the middle
99.7% of customers have to wait.
Answers
Answer:
.........................
Step-by-step explanation:
.................................................
Answer:
99.7% of customers have to wait between 8 minutes to 30 minutes for their food.
Step-by-step explanation:
We are given the following in the question:
Mean, μ = 18 minutes
Standard Deviation, σ = 3 minutes
We are given that the distribution of amount of time is a bell shaped distribution that is a normal distribution.
Empirical Formula:
Almost all the data lies within three standard deviation from the mean for a normally distributed data.
About 68% of data lies within one standard deviation from the mean.
About 95% of data lies within two standard deviations of the mean.
About 99.7% of data lies within three standard deviation of the mean.
Thus, 99.7% of the customers have to wait:
`
Thus, 99.7% of customers have to wait between 8 minutes to 30 minutes for their food.
hope this helps
plz can i get brainliest:)