Expand. Your answer should be a polynomial in standard form. (-p^2+4p-3)(p^2+2)=(−p 2 +4p−3)(p 2 +2)=left parenthesis, minus, p, squared, plus, 4, p, minus, 3, right parenthesis, left parenthesis, p, squared, plus, 2, right parenthesis, equals
Answers
The expansion of the polynomial (-p²+4p-3)(p²+2) would be is -p⁴ + 4p³ - 5p² + 8p - 6
Here we need to expand the polynomial (-p²+4p-3)(p²+2)
To do so we need to multiply each of the term with the first bracketby the each term of second bracket.
So, the expansion of the polynomial (-p²+4p-3)(p²+2) would be,
(-p² + 4p - 3)(p² + 2)
= [p² × (-p² + 4p - 3)] + [2 × (-p² + 4p - 3)]
= [p² × (-p²) + p² × 4p - p² × 3] + (-2p² + 8p - 6)
= (-p⁴ + 4p³ - 3p²) + (-2p² + 8p - 6)
= -p⁴ + 4p³ - (3 + 2)p² + 8p - 6 .......(add like terms)
= -p⁴ + 4p³ - 5p² + 8p - 6
Therefore, the required polynomial is -p⁴ + 4p³ - 5p² + 8p - 6
Learn more about the polynomial here:
https://brainly.com/question/11536910
#SPJ4
Related Questions
What is the sum of the prime factors of the number 330?
Answers
Answer:
21
Step-by-step explanation:
prim factors: 2, 3, 5, and 11
The sum of the prime factors of the number 330 is 21.
What is a prime factor?A natural number other than 1 whose only factors are 1 and itself is said to have a prime factor. In actuality, the first few prime numbers are 2, 3, 5, 7, 11, and so forth.
Given:
The number is 330
Factorize the above number,
330 = 1 × 2 × 3 × 5 × 11
Prime factors are = 2, 3, 5, 11
Calculate the sum of the prime factor
2 + 3 + 5 + 11 = 21
Therefore, the sum of the prime factors of the number 330 is 21.
To know more about prime factors:
https://brainly.com/question/19235147
#SPJ6
a. Find the ratio of the number of nonfiction book to the number of fiction books give your answer in fraction form. Give your answer in fraction form
b. How many times the number of nonfiction books is the number of fiction books? Give your answer in fraction form.
c. Suppose the number fiction books is 2/7 times the number of nonfiction books what would be the ratio of the number of nonfiction books to the number of TOTAL number of books give your answer in fraction form.
Answers
The ratio of nonfiction to fiction books is 49 : 2.
What are ratio and proportion?In its most basic form, a ratio is a comparison between two comparable quantities.
There are two types of proportions One is the direct proportion, whereby increasing one number by a constant k also increases the other quantity by the same constant k, and vice versa.
If one quantity is increased by a constant k, the other will decrease by the same constant k in the case of inverse proportion, and vice versa.
Given, The number of fiction books is 2/7 times the number of nonfiction books.
So, If we have 7 nonfiction books then we have 2/7 fiction books.
Therefore, The ratio Nonfiction : Fiction = 7 : 2/7.
Nonfiction : Fiction = 49 : 2.
learn more about ratios here :
https://brainly.com/question/13419413
#SPJ1
A certain test preparation course is designed to help students improve their scores on the GRE exam. A mock exam is given at the beginning and end of the course to determine the effectiveness of the course. The following measurements are the net change in 7 students' scores on the exam after completing the course:
24,6,21,8,16,10,18
Using these data, construct a 80% confidence interval for the average net change in a student's score after completing the course. Assume the population is approximately normal
Step 1:Calculate the sample mean for the given sample data. Round your answer to one decimal place.
Step 2:Calculate the sample standard deviation for the given sample data. Round your answer to one decimal place.
Step 3:Find the critical value that should be used in constructing the confidence interval. Round your answer to three decimal places.
Step 4:Construct the 80% confidence interval. Round your answer to one decimal place (Lower endpoint, Upper endpoint)
Answers
Step 1: The sample mean is (24+6+21+8+16+10+18)/7 = 15.7 (rounded to one decimal place)
Step 2: The sample standard deviation is calculated using the formula:
s = sqrt[(Σ(x - mean of x)^2) / (n - 1)]
where Σ is the sum of the squared deviations from the mean, mean of x is the sample mean, and n is the sample size.
Using the given data, we get:
s = sqrt[((24-15.7)^2 + (6-15.7)^2 + (21-15.7)^2 + (8-15.7)^2 + (16-15.7)^2 + (10-15.7)^2 + (18-15.7)^2) / (7-1)]
s = 6.679 (rounded to one decimal place)
Step 3: To find the critical value, we use a t-distribution with n-1 degrees of freedom and a confidence level of 80%. From a t-distribution table or using a calculator, we find the critical value to be 1.397 (rounded to three decimal places).
Step 4: Using the formula for the confidence interval:
CI = mean of x ± t*(s / sqrt(n))
where mean of x is the sample mean, t is the critical value, s is the sample standard deviation, and n is the sample size.
Plugging in the values, we get:
CI = 15.7 ± 1.397*(6.679 / sqrt(7))
CI = (9.47, 21.93)
So the 80% confidence interval for the average net change in a student's score after completing the course is (9.47, 21.93).
Visit here to learn more about sample mean brainly.com/question/31101410
#SPJ11
11. What is the area of the triangle ABC if a=4, b= 7, and B= 75°?
Answers
If a=4, b= 7, and B= 75°, the area of triangle ABC is approximately 13.476 square units.
To find the area of triangle ABC given the values of a, b, and B, we can use the formula:
Area = (1/2) * a * b * sin(B)
where a and b are the lengths of two sides of the triangle and B is the angle between them, measured in degrees.
Substituting the given values, we get:
Area = (1/2) * 4 * 7 * sin(75°)
Using a calculator to evaluate the sine of 75°, we get:
Area = (1/2) * 4 * 7 * 0.96593
Area ≈ 13.476 square units
The formula for the area of a triangle involves using the length of two sides and the angle between them.
To learn more about area click on,
https://brainly.com/question/29648395
#SPJ4
Assume that A and B are n * n matrices with det A = 6 and det B = -2. Find the indicated determinant. Det (B^-1 A) det (B^-1 A) =
Answers
The value of the determinant det(B⁻¹ A) is -3.
We want to find the determinant of the product of matrices B⁻¹ and A, which can be written as det(B⁻¹ A).
Given that det(A) = 6 and det(B) = -2, you can use the following properties of determinants:
1. det(AB) = det(A) * det(B) for any square matrices A and B.
2. det(A⁻¹) = 1/det(A) for any invertible matrix A.
Now, let's find the determinant of the given product:
det(B⁻¹A) = det(B⁻¹) * det(A) by property 1.
Since det(B) = -2, we can find det(B⁻¹) using property 2:
det(B⁻¹) = 1/det(B) = 1/(-2) = -1/2.
Now, substitute the known values of det(A) and det(B⁻¹) into the equation:
det(B⁻¹ A) = det(B⁻¹) * det(A) = (-1/2) * 6 = -3.
So, the determinant of the product B⁻¹A is -3.
Learn more about a determinant:
https://brainly.com/question/16981628
#SPJ11
suppose that the slope parameter in a simple linear regression model is β1 = 3.52. what does this suggest about the nature of the relationship between x and y?
Answers
A slope parameter of β1 = 3.52 in a simple linear regression model suggests that there is a positive and direct relationship between the independent variable (x) and the dependent variable (y).
Specifically, for every one unit increase in the independent variable (x), the dependent variable (y) is expected to increase by an average of 3.52 units. This indicates a positive linear association between x and y, implying that as x increases, y tends to increase as well.
The magnitude of the slope parameter (3.52) also indicates the steepness of the relationship. A larger slope suggests a stronger relationship, indicating that the change in y for a given change in x is relatively large.
Learn more about parameter here : brainly.com/question/14350133
#SPJ11
justin is driving from riverton to rock springs, a distance of 144 miles. he plans to stop along the way for 15 minutes. how fast must justin drive in order to averafe 64 miles per hour for the whole trip, including the time when he stops
Answers
Justin must drive at least 67.2 miles per hour (rounded to one decimal place) to average 64 miles per hour for the whole trip, including the 15-minute stop
To average 64 miles per hour for the whole trip, Justin must complete the 144-mile distance and the 15-minute stop in a total of 144 minutes (2 hours and 24 minutes) or less.
If we subtract the 15 minutes stop from the total time, Justin will have to cover the 144 miles in 129 minutes (2 hours and 9 minutes) or less.
To determine the required speed, we can use the formula:
\(speed = \frac{distance }{time}\)
So, \(speed = \frac{144 miles}{129 minutes}=1.12 miles per minute\)
To convert this to miles per hour, we can multiply by 60:
1.12 miles per minute x 60 minutes per hour = 67.2 miles per hour
Therefore, Justin must drive at least 67.2 miles per hour (rounded to one decimal place) to average 64 miles per hour for the whole trip, including the 15-minute stop.
To know more about "Speed" refer here:
https://brainly.com/question/3004254#
#SPJ11
On a spinner I have a 0.1% chance of getting a 5. How many times do I need to spin to get 5?
Answers
Answer:
\(\frac{1}{10} * \frac{1}{100} = \frac{1}{1000}\)
1000 times
Step-by-step explanation:
Answer:
0.1% = 1 spin then
100% = ( 100×1) ÷0.1 = 1000
we are using 100% because its a sure bet it will happen but not logically
the answer is 1000
the ratio of the side length of square A to the side length of square B is 3 : 5. the perimeter of square B IS 60 feet. what is the area of square A?
Answers
Answer:
81 square ft
Step-by-step explanation:
square B has a site lenght of 15ft
therefore square must have one of 3/5 of 15 which is 9
the area is 9x9=81
If team A is the underdog in playing team B and has probability 1/3 of winning every game it plays against team B. What is the probability that it wins the best-of-five series over team B? Note: Team A must win the last game played.
Answers
The probability that team A wins the best-of-five series over team B is 32/243.
For team A to win the best-of-five series over team B, team A must win at least three of the five games played, and the last game played must be a win for team A. Let's consider the different ways that team A can win the series:
Team A wins the first three games and loses the last two games.
Team A wins the first two games, loses the third game, wins the fourth game, and loses the fifth game.
Team A wins the first two games, loses the third game, loses the fourth game, and wins the fifth game.
Team A wins the first game, loses the second game, wins the third game, loses the fourth game, and wins the fifth game.
The probability of each of these outcomes is:
(1/3)^3 * (2/3)^2 = 8/243
(1/3)^2 * (2/3) * (1/3) * (2/3) = 8/243
(1/3)^2 * (2/3) * (2/3) * (1/3) = 8/243
(1/3) * (2/3) * (1/3) * (2/3) * (1/3) = 8/243
Therefore, the probability that team A wins the best-of-five series over team B is the sum of these probabilities:
P(A wins series) = 8/243 + 8/243 + 8/243 + 8/243 = 32/243
So, the probability that team A wins the best-of-five series over team B is 32/243.
To learn more about probability visit:https://brainly.com/question/30034780
#SPJ11
i dont know
what to do here and its due by the end of class

Answers
Answer:
ur screwed but the answer is 110.88
Step-by-step explanation:
:)
If a voter votes RIGHT in one election, the probability that the voter will vote LEFT in the next election is 0.2. If a voter votes LEFT in one election, the probability that the voter will vote RIGHT in the next election is 0.1. Assume that these are the only two parties available to vote for. 1. What is the Markov assumption? 2. Draw the transition diagram to this problem. 3. Write down the transition matrix. 4. If 55% of the electorate votes RIGHT one year, find the percentage of voters who vote RIGHT the next year. What would be the voter percentages in 10 years' time? Interpret your result. (2+2+3 marks) 5. Will there ever be a steady state where the party percentages don't waiver? Interpret your result. (3+3 marks)
Answers
After 10 years, the voter percentages would be approximately 50.3% for LEFT and 49.7% for RIGHT.
The Markov assumption in this context is that the probability of a voter's next vote depends only on their current vote and not on their past voting history. In other words, the Markov assumption states that the future behavior of a voter is independent of their past behavior, given their current state.
Transition diagram:
LEFT RIGHT
|--------->--------|
LEFT | 0.8 0.2 |
| |
RIGHT| 0.1 0.9 |
|--------->--------|
The diagram represents the two possible states: LEFT and RIGHT. The arrows indicate the transition probabilities between the states. For example, if a voter is currently in the LEFT state, there is a 0.8 probability of transitioning to the LEFT state again and a 0.2 probability of transitioning to the RIGHT state.
Transition matrix:
| LEFT | RIGHT |
---------------------------
LEFT | 0.8 | 0.2 |
---------------------------
RIGHT | 0.1 | 0.9 |
---------------------------
The transition matrix represents the transition probabilities between the states. Each element of the matrix represents the probability of transitioning from the row state to the column state.
If 55% of the electorate votes RIGHT one year, we can use the transition matrix to find the percentage of voters who vote RIGHT the next year.
Let's assume an initial distribution of [0.45, 0.55] for LEFT and RIGHT respectively (based on 55% voting RIGHT and 45% voting LEFT).
To find the percentage of voters who vote RIGHT the next year, we multiply the initial distribution by the transition matrix:
[0.45, 0.55] * [0.2, 0.9; 0.8, 0.1] = [0.62, 0.38]
Therefore, the percentage of voters who vote RIGHT the next year would be approximately 38%.
To find the voter percentages in 10 years' time, we can repeatedly multiply the transition matrix by itself:
[0.45, 0.55] * [0.2, 0.9; 0.8, 0.1]^10 ≈ [0.503, 0.497]
After 10 years, the voter percentages would be approximately 50.3% for LEFT and 49.7% for RIGHT.
Interpretation: The results suggest that over time, the voter percentages will tend to approach an equilibrium point where the percentages stabilize. In this case, the percentages stabilize around 50% for both LEFT and RIGHT parties.
No, there will not be a steady state where the party percentages don't waiver. This is because the transition probabilities in the transition matrix are not symmetric. The probabilities of transitioning between the parties are different depending on the current state. This indicates that there is an inherent bias or preference in the voting behavior that prevents a steady state from being reached.
Learn more about probability at:
brainly.com/question/13604758
#SPJ4


Which of the following functions is graphed below?
Answers
Answer:
there are no functions her pls add them for an answer:)
Step-by-step explanation:
Which method would be best (quickest) for solving the system below:
3x - 4y = -2
y = 2x + 1
Answers
Write the equations under one another, like this:
2x - y = -1
+ 3x + 4y = 26
Ideally, we would like for one of the variables to be eliminated when we add vertically (straight down). But if we add them as they are this does not happen. We must manipulate one of the equations so that it will happen. Again, you can try to eliminate either x or y. I always look for a term that has a coefficient of 1 (or negative 1). So, let's use that y from the first equation again.
If the coefficient of the y in the other equation is POSITIVE 4, then I need the coefficient from the first equation to be its opposite, NEGATIVE 4. To do this, simply multiply the first equation by 4, this will create MAGIC!
4( 2x - y = -1)
+ 3x + 4y = 26
Be certain to Distribute across the entire first equation, so multiply all three terms by 4.
8x - 4y = -4
+ 3x + 4y = 26
Now add straight down (vertically). The y term will be eliminated.
11x = 22
Divide both sides of the equation by 11.
x = 2
Almost there! Now, substitute the 2 in for x in either of the original equations. Either one will work. I'm gonna use the second equation.
3x + 4y = 26
3(2) + 4y = 26
6 + 4y = 26
Subtract 6 from both sides of the equation.
4y = 20
Divide both sides of the equation by 4.
y = 5
That's it! There it is again. Put it all together. If x = 2 and y = 5, then the solution is the ordered pair, (2,5).
A data set has these values: 6, 8, 8, 10, 10, 10, 10, 12, 12, 14. The histogram of
the distribution is shown.
Frequency
5
4
3
21
0
11
Data values
5 7 9
13 15
Which statement does not describe the data set?
Answers
The statement that does not describe the data set 6, 8, 8, 10, 10, 10, 10, 12, 12, 14 is:
(C) The range of the data set is 15.
Consider the data set,
6, 8, 8, 10, 10, 10, 10, 12, 12, 14
The mean of the data set will be:
mean = ( 6 + 8 + 8 + 10 + 10 + 10 + 10 + 12 + 12 + 14 )/ 10
mean = 100/10
mean = 10
The data set in ascending order are:
6, 8, 8, 10, 10, 10, 10, 12, 12, 14
As the number of terms is even. Therefore, the median will be the sum of two middle numbers divided by 2.
So,
Median = ( 10 + 10 )/2 = 20/2 = 10
The mode of a data set is the maximum number of times a number appears in the data set.
Therefore, the mode of the data set is 10.
The range of the data set is the difference between the highest and the lowest number in the data set.
Range = 14 - 6 = 12
The data set is a symmetric distribution if the mean, median, and mode all fall at the same point.
As the mean, median, and mode are 10, 10, and 10 respectively. Hence, the data set is symmetric.
Hence, statements (A), (B), and (D) are true.
Learn more about mean, median, and mode here:
brainly.com/question/14532771
#SPJ1

2) Julie wants to purchase swim lessons for her son. There are four different stores that offer swim lessons. Based on the lowest cost per minute, which store has the BEST deal ?
Store A: $25 for a 45 minute lesson, Store B: $30 for a 1 hour lesson, Store C: $45 for a 1.5 hour lesson, and Store D: $80 for three 1 hour lessons
Answers
Store C offers the best deal
Based on the lowest cost per minute, Store C has the best deal. It charges $45 for a 1.5 hour lesson, which works out to $0.30 per minute. The other stores charge more per minute: Store A charges $0.56 per minute, Store B charges $0.50 per minute, and Store D charges $0.40 per minute for each of the three 1 hour lessons.
Store A has the highest cost that is $0.56 per minute
Next Store B comes in the 2nd place which costs around $0.50 per minute.
After that Store D charges at the rate of $0.40 per minute.
Store C offers the best deal which is $0.30 per minute.
To know more about minute conversion visit: brainly.com/question/15600126
#SPJ4
Water flows through a hose and fills a 100-gallon tank in eight minutes. When represented as a rate, in gallons per minute, what is the unit rate?
800
0.08
18
12.5
Answers
Answer:
0.08.
Step-by-step explanation:
Answer:
12.5
Step-by-step explanation:
A gardener wants to divide a square piece of lawn in half diagonally. what is the length of the diagonal side of the square is 8 ft ? leave your answer in simplest radical form.a. 16b.2c.8d. 4
Answers
The length of the diagonal side is 82, or answer (d) in its simplest radical form.
The Pythagorean Theorem must be utilized in order to determine the length of the diagonal side of a square with a length of 8 feet. You can use the formula a2 + b2 = c2, where a and b are the sides of the triangle and c is the hypotenuse, since the diagonal side of the square is. Because a and b are both 8 feet, you can use those numbers to solve for c:
82 + 82 = c2 64 + 64 = c2 128 = c2 The length of the diagonal side is 82, or answer d in its simplest radical form.
Learn more about Radical Form:
https://brainly.com/question/28519153
#SPJ4
helpppppppppppppppppppppppppppp

Answers
Answer:
hii
Step-by-step explanation:
I don't know what is the answer
Answer:
use formula
Step-by-step explanation:
and solve step by step hope it helpd
Need help ASAP !!! And show work please

Answers
Answer:
\(\sqrt{40}\) or 6.32
Step-by-step explanation:
We can find the distance between two points by using this formula
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
where the x and y values are derived from the given points
The points given are ( -2 , 5 ) and ( 4 , 3 )
So we plug in the x and y values of those coordinates into the distance formula
\(\sqrt{(4-(-2)^2+(3-5)^2} \\4-(-2)=6\\3-5=-2\\d=\sqrt{6^2+-2^2} \\6^2=36\\-2^2=4\\36+4=40\\d=\sqrt{40}\)
or 6.32
Using the equality of surds theorem, solve this question
In the question solve for a and b
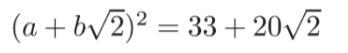
Answers
Step-by-step explanation:
76.72135955 is the answer I think So if the answer is correct then plz mark me as brainliest
What is the perimeter of the parallelogram?
A 12
B 15
C 30
D 44

Answers
Answer:
C. P = 30
Step-by-step explanation:
Parallelogram opposite (or parallel) sides are equal,
so:
2x = x + 2
5y - 9 = 2y + 3
For x:
2x = x + 2
2x - x = 2
x = 2
For y:
5y - 9 = 2y + 3
5y - 2y = 3 + 9
3y = 12
y = 4
the smallest sides are equal 2x and x + 2 => 2 * 2 = 4
the biggest sides are equal 5y - 9 and 2y + 3 => 2 * 4 + 3 = 11
P = 2 * (a + b)
P = 2 * (4 + 11)
P = 2 * 15
P = 30
Help!! Stuff about triangles

Answers
Answer:
3
Step-by-step explanation:
Since \(\angle A \cong \angle A\) by the reflexive property and \(\angle ABC \cong \angle ADE\) since they are both right angles, \(\triangle ABC \sim \triangle ADE\) by AA.
It follows that:
\(\frac{x}{9}=\frac{5}{9+6} \implies x=3\)
You run 6 miles in 1 hour. At this rate, how much time it will take you to run 27 miles? Answer in hours and minutes.
Answers
Answer:
4hours and 30 minutes
Step-by-step explanation:
27/6=4.5
Mrs Ong bought some fruits. 3 fewer than 1/2 of the fruits were oranges. 2 fewer than 1/2 of the remaining fruits were pears. 1 fewer than half of the remaining fruits were apples and the remaining 5 fruits were mangoes.
(a) How many fruits did Mrs Ong buy altogether?
(b) What fraction of the fruits were pears? Give your answer in the simplest form.
Answers
Using algebra we can conclude that Mrs. Ong brought a total of 12 fruits.
What is Algebra?Algebra is a discipline of mathematics that studies symbols and the mathematical operations that can be applied to them.
These symbols are referred to as variables because they don't have predetermined values.
These symbols are also subjected to various addition, subtraction, multiplication, and division arithmetic operations in order to ascertain the values.
Now, let the total fruits be x.
Oranges = 1/2 x - 3
Pears = [x - 1/2 (1/2x -3 ) ]- 2= x - 1/4x + 3/2 - 2 = 3x /4 - 1/2
Apples = x - 1/2 (3x /4 - 1/2) - 1
= x - 3/8 x + 1/4 - 1 = 5x /8 - 3/4
Mangoes = 5
x - 5x/ 8 + 3/4 = 5
3x /8 + 3/4 = 5
3x + 6 = 40
3x = 34
x = 11.333
Therefore, using algebra we can conclude that Mrs. Ong brought a total of 12 fruits.
Learn more about algebra here:
brainly.com/question/24875240
#SPJ1
Complete question:
Mrs. Ong bought some fruits. 3 fewer than 1/2 of the fruits were oranges. 2 fewer than 1/2 of the remaining fruits were pears. 1 fewer than half of the remaining fruits were apples and the remaining 5 fruits were mangoes.
How many fruits did Mrs Ong buy altogether?
Is Jennifer or Jacqueline correct?

Answers
Answer:
Jennifer
Step-by-step explanation:
The domain of a function is the set of x-values that result in defined and real values for that function.
In this case the requirement was to plot a graph so that the domain is between -4 and 5 inclusive
We can represent this mathematically as -4 ≤ x ≤ 5
If you look at both graphs, Ashton's graph on the left has a minimum
x-value of -4 and a maximum x-value of 5. So his graph is correct
Carlie's graph on the right does have a minimum x-value of -4 but its maximum x-value is between 2 and 3. So this graph is incorrect
Therefore Jennifer's statement is correct
Answer: Jennifer
suppose there are a black balls and b white balls in a jar. we randomly pick a ball from the jar and put it back until we have a white ball. denote x as the number of balls we have picked. what would be the distribution and expectation of x? (the distribution is the general formula for P(x=k)
for each
k∈N)
. (You should derive the expectation from the definition).
Answers
It is the sum of the product of the number of trials and the probability of getting a white ball in that trial. E(X) = 1(1-p) + 2(1-p)p + 3(1-p)p2 + ....= 1 + (1-p)p + (1-p)p2 + ....= 1/p = (a+b)/b = (a/b) + 1.
Suppose there are a black balls and b white balls in a jar. We randomly pick a ball from the jar and put it back until we have a white ball. Denote x as the number of balls we have picked. What would be the distribution and expectation of x? (the distribution is the general formula for P(x=k) for each k ∈ N). (You should derive the expectation from the definition).The probability of picking a white ball is p = (b/(a+b)).
Then the probability of getting a white ball after x-1 black balls would be (1-p)x-1p. The distribution can be given as:P(x=k) = (1-p)k-1pSince we are choosing balls randomly, the balls' outcomes are independent of each other. Therefore, the distribution of x is given by the geometric distribution. The expectation is the total number of trials required to get a white ball.
Learn more about Black balls
brainly.com/question/31171032
#SPJ11
a) about what percentage of scores were between between 68 and 82? 68 % b) about what percentage of scores were between 61 and 75?
Answers
Therefore , the percentage of case 1 is 68% and percentage of case 2 is 47.4%
What is percentage?One percent (symbolized as 1%), being the hundredth component, is represented as 100 percent, while 200 percent signifies twice the amount specified. As an illustration, 1% of 1,000 chickens is equal to 1/100 of 1,000, or 10 birds, and 20% of the quantity is equal to 20% of 1,000, or 200.
Here,
Given: Total number of freshman =500
mean =75 and standard deviation =7
a) the percentage of scores that fell between 68 and 82
340 is the number of freshman whose scores that fell between 68 and 82
thus,
percentage = 340 /500 * 100
=> percentage = 68%
b)the percentage of scores that fell between 61 and 75
237 is the number of freshman whose scores that fell between 61 and 75
thus,
percentage = 237/500 * 100
=> percentage = 47.4%
Therefore , the percentage of case 1 is 68% and percentage of case 2 is 47.4%
To know more about percentage , visit
https://brainly.com/question/1578304
#SPJ4
For the standard normal random variable z, find z for each situation. If required, round your answers to two decimal places. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300)'
a. The area to the left of z is 0.1827. z =
b. The area between −z and z is 0.9830. z =
c. The area between −z and z is 0.2148. z =
d. The area to the left of z is 0.9997. z =
e. The area to the right of z is 0.6847. z=
Answers
The z-values for the given situations are approximate:
a. The area to the left of z is 0.1827. z = -0.90
b. The area between −z and z is 0.9830. z = 2.17
c. The area between −z and z is 0.2148. z = 0.85
d. The area to the left of z is 0.9997. z = 3.49
e. The area to the right of z is 0.6847. z= -0.48
a. For an area of 0.1827 to the left of z, the corresponding z-value can be found using a standard normal distribution table or a statistical calculator. The z-value is approximately -0.90.
b. To find the z-value for an area between -z and z equal to 0.9830, we need to find the value that corresponds to (1 - 0.9830)/2 = 0.0085 in the upper tail of the standard normal distribution. Using the table or calculator, the z-value is approximately 2.17.
c. Similarly, for an area between -z and z equal to 0.2148, we find the value that corresponds to (1 - 0.2148)/2 = 0.3926 in the upper tail. The z-value is approximately 0.85.
d. For an area of 0.9997 to the left of z, we find the value that corresponds to 0.9997 in the upper tail. The z-value is approximately 3.49.
e. To find the z-value for an area to the right of z equal to 0.6847, we find the value that corresponds to 1 - 0.6847 = 0.3153 in the upper tail. The z-value is approximately -0.48.
In summary, the z-values for the given situations are approximate:
a. -0.90
b. 2.17
c. 0.85
d. 3.49
e. -0.48
These values can be used to determine the corresponding percentiles or probabilities for the standard normal distribution. The values are typically found using standard normal distribution tables or statistical calculators that provide the cumulative probability distribution function (CDF) for the standard normal distribution.
For more such answers on z-values
https://brainly.com/question/28000192
#SPJ8
Jack drove 520 miles on his trip. If he was going 65 miles per hour, how many hours did he drive?
Answers
Answer:
8 hours
Step-by-step explanation:
520 miles divided by 65mph