Eloise practiced piano for 25 of an hour. Sarah practiced piano for 34 of an hour.
How much longer did Sarah practice than Eloise?
Enter your answer as a fraction in simplest form by filling in the boxes.
first one gets brainiest
Answers
2/5 and 3/4 need the same second half so 2/5 and 3/4 = 8/20 and 15/20
15/20 - 8/20 - 7/20.
Sarah practiced 7/20 of an hour more than Eloise.
This can not be simplified.
7/12.
Math isn't my best subject, sorry if incorrect.
Related Questions
Leah has an account balance of -150 dollars. Which of the following represents a debt greater than -150 dollars? - 175 dollars - 150 dollars -125 dollars 0 dollars
Answers
Owing 175 dollars is more than owing 150 dollars.
Thereby, the correct answer is A) -175 dollars
............................................................... .
Answers
Please help thank you

Answers
Can somebody please help me!!

Answers
Step-by-step explanation:
Simply you replace X and Y by their values
Given: x=-1 y=-4
10 - (-X)^3 + y^2
=10 + X^3 + Y^2
Now replace X and Y
=10 + (-1)^3 + (-4)^2
=10 - 1 + 16
= 25
Which of the following is an equivalent representation of 5-4 ?
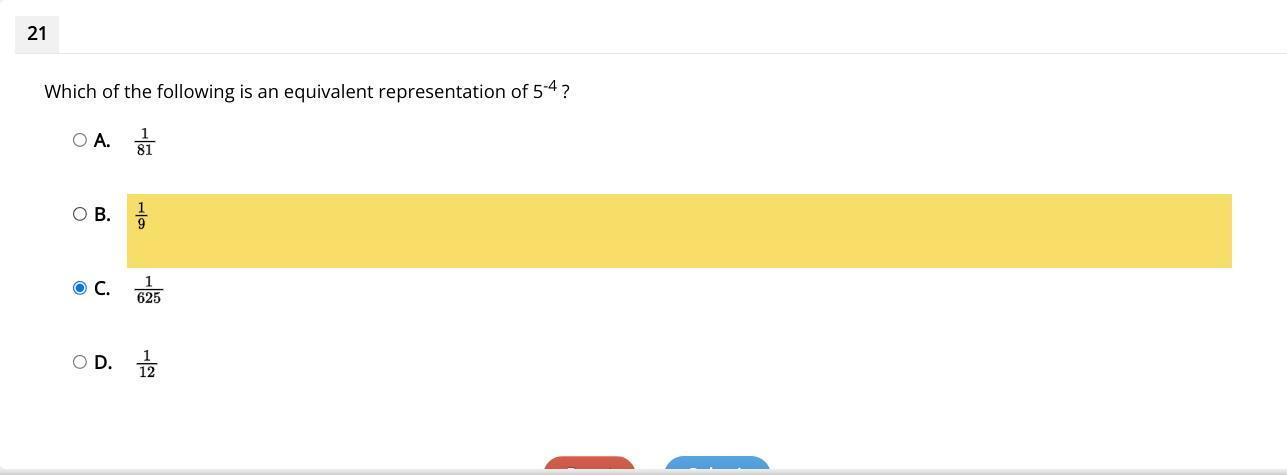
Answers
1/5^4
Raise 5 to the power 4
1/625
HELP ME WITH THIS PROBLEM PLEASE!!

Answers
Answer:
w ≈ 33.9 in
Step-by-step explanation:
Using Pythagoras' identity in the right triangle
w² + w² = 48²
2w² = 2304 ( divide both sides by 2 )
w² = 1152 ( take the square root of both sides )
w = \(\sqrt{1152}\) ≈ 33.9 in ( to the nearest tenth )
The axis of symmetry for the graph of the function f start bracket x end bracket equals one-quarter x square plus b x plus 10 is x=6. What is the value of b?−12−31/23
Answers
Given that the axis of symmetry for the graph of the function f (x) = 1/4x² + bx + 10 is x = 6.The formula to find the axis of symmetry of a quadratic function is given by; x = - b/2a
Since the given function is already in vertex form, the value of the axis of symmetry can be read directly from the formula. The vertex form of a quadratic function is given by; f (x) = a(x - h)² + k Where (h, k) is the vertex of the parabola. Comparing this to the given function, we have; h = 0 and k = 10Therefore, the axis of symmetry is x = h = 0The equation x = - b/2a gives us b = -12Thus, the value of b is -12. Hence, the correct option is −12.
Learn more about graph here:
https://brainly.com/question/25477902
#SPJ11
What is the place value of the 9 in 67.49?
Answers
Find the midpoint of the line segment with end coordinates of: (-3,-1)and(-4,2)
Give coordinates as decimals where appropriate.
Answers
Answer:
The answer for this question is (-3.5,0.5)
Susan made 168 cupcakes and gave some to her 21 students.
She then had 1/2 of her cupcakes left. On average, how many
cupcakes did she give to each of the 21 students?
Answers
Answer:
4
Step-by-step explanation:
The smallest angle of rotational symmetry for a regular polygon is 30°. How many sides does the regular polygon have?
Answers
At what input value will the function
f(x) = -x - 2 + 2 begin to have real
outputs?
x = [?]
Answers
Answer:
All real numbers.
Step-by-step explanation:
f(x) = -x - 2 + 2
~Combine like terms
f(x) = -x
This function does not have any constraints so x can be equal too any real number.
Best of Luck!
Answer: -2
Step-by-step explanation:
add two to both sides
X-2<0
-X<2
Times -1 to both side
X<-2
Flip the sign When you have a negative.
The least common denominator of\(\frac{1}{6} and \frac{5}{12}\) is 12.
TrueFalse
Answers
In one year, there were 116 homicide deaths in Richmond, Virginia. Using the Poisson distribution, find the probability that the number of homicide deaths for a randomly selected day is:
a) 0
b) 1
c) 2
Answers
The probability that the number of homicide deaths for a randomly selected day is:
a) 0: 0.18,
b) 1: 0.35,
c) 2: 0.27
The Poisson distribution is used to simulate the likelihood that a certain number of events will occur within a predetermined window of time or space.
In this instance, the Poisson distribution can be used to simulate the number of homicide deaths that occurred in Richmond, Virginia over the course of a year.
The Poisson distribution can be used to determine the likelihood of 0, 1, and 2 homicides happening on any given day.
One homicide occurs on a randomly chosen day with a 0.18 percent chance, one homicide occurs on a randomly chosen day with a 0.35 percent chance, and two homicides occur on a randomly selected day with a 0.27 percent chance.
Complete Question:
In one year, there were 116 homicide deaths in Richmond, Virginia. Using the Poisson distribution, find the probability that the number of homicide deaths for a randomly selected day is:
a) 0
b) 1
c) 2
To learn more about probability visit:
https://brainly.com/question/24756209
#SPJ4
Find the value of each variable

Answers
Answer:
x = 22, y = 12.
Step-by-step explanation:
5x + 4 = 114 (opposite angles).
5x + 4 + 3x - 24 + 2y = 180 (adjacent angles are supplementary)
From first equation:
5x = 110
x = 22.
Substituting for x in the second equation:
114 + 3(22) - 24 + 2y = 180
2y = 180 - 114 - 66 + 24
2y = 24
y = 12.
The base lengths of a trapezoidal tabletop are 6 feet and 8 feet. the height is 4 feet. what is the area
Answers
The area is 28 square feet.
The formula to find the area of a trapezoid is (base1 + base2) * height / 2. In this case, the base lengths are 6 feet and 8 feet, and the height is 4 feet. So, we can substitute these values into the formula.
Using the formula, we get:
Area = (6 + 8) * 4 / 2
= 14 * 4 / 2
= 56 / 2
= 28 square feet
Therefore, the area of the trapezoidal tabletop is 28 square feet.
A trapezoid is a quadrilateral with one pair of parallel sides. The bases of a trapezoid are the parallel sides, and the height is the perpendicular distance between the bases. To find the area of a trapezoid, we multiply the sum of the bases by the height, and then divide by 2.
In this case, the sum of the bases is 6 + 8 = 14. Multiplying 14 by the height of 4 gives us 56. Dividing 56 by 2 gives us the final answer of 28 square feet.
Know more about trapezoid here:
https://brainly.com/question/31380175
#SPJ11
the surface area of a sphere is 1. what is the surface area (including the base area) of a hemisphere with the same radius?
Answers
If the surface area of a sphere is 1, then its radius is √(1/4π) = 0.2821 (approximate to four decimal places).
The surface area of a hemisphere with the same radius is half that of the sphere since it only covers half of the surface area.
So, the surface area (including the base area) of the hemisphere would be:
2π(0.2821)^2 + π(0.2821)^2 = 0.5 + 0.25π = 0.7854 (approximate to four decimal places).
Therefore, the surface area (including the base area) of the hemisphere with the same radius is approximately 0.7854 square units.
Hi! To find the surface area of a hemisphere with the same radius as a sphere, we'll first determine the radius using the sphere's surface area formula, and then apply the hemisphere's surface area formula.
1. Sphere's surface area formula: A = 4πr²
Given surface area A = 1, we'll solve for radius r:
1 = 4πr²
Divide both sides by 4π:
1 / 4π = r²
2. Find r:
r = √(1 / 4π)
3. Hemisphere's surface area formula (including base area): A_hemisphere = 3πr²
Substitute r with the value we found:
A_hemisphere = 3π(√(1 / 4π))²
4. Simplify the expression:
A_hemisphere = 3π(1 / 4π)
A_hemisphere = (3/4)π
So, the surface area (including the base area) of the hemisphere with the same radius as the given sphere is (3/4)π.
know more
https://brainly.com/question/31464920
#SPJ11
Which of the following is a solution to the equation: tan(x+pi/4) = cotx
a. -0.414
b. -1.883
c. -3pi/8
d. 2.424
Answers
None of the options represent Values that are multiples of π, and therefore, none of them satisfy the equation sin(x) = 0. Thus, none of the given options is a solution to the equation tan(x + π/4) = cot(x).
To determine which of the given options is a solution to the equation tan(x + π/4) = cot(x), we can use the trigonometric identities and properties.
Recall that tan(x) is equal to sin(x)/cos(x), and cot(x) is equal to cos(x)/sin(x). Substituting these expressions into the equation, we have:
sin(x + π/4)/cos(x + π/4) = cos(x)/sin(x)
Next, let's simplify the equation by cross-multiplying:
sin(x + π/4) * sin(x) = cos(x + π/4) * cos(x)
Now, we can use the trigonometric identity sin(a + b) = sin(a)cos(b) + cos(a)sin(b) to rewrite the equation as follows:
(sin(x)cos(π/4) + cos(x)sin(π/4)) * sin(x) = cos(x)cos(π/4) * cos(x)
Simplifying further:
(√2/2)sin(x) + (√2/2)cos(x) = (√2/2)cos(x)
Now, let's simplify the equation by subtracting (√2/2)cos(x) from both sides:
(√2/2)sin(x) = 0
From this equation, we can see that sin(x) = 0, which occurs when x is a multiple of π (x = nπ, where n is an integer).
Looking at the given options:
a. -0.414
b. -1.883
c. -3π/8
d. 2.424
None of the options represent values that are multiples of π, and therefore, none of them satisfy the equation sin(x) = 0. Thus, none of the given options is a solution to the equation tan(x + π/4) = cot(x).
For more questions on Values .
https://brainly.com/question/843074
#SPJ8
Mr. vazquez determines that the area of a bathroom in his house is 25 square feet less than 1/5 of the area of the living room if the bathroom measures 35 square feet what is the area of the living room ?
Answers
Answer:200
Step-by-step explanation:
Multiply 35 by 5 to get 175. You do this because you are doing the opposite to find a larger amount. Then add 25 to get 200
1.) The signature on the line on the bottom right hand corner of a check should always be written:
A.) in cursive writing.
B.) in printed writing.
C.) in either cursive or printed writing.
D.) with the initials of the check signer.
E.) None of these choices are correct.
Answers
Answer:
below
Step-by-step explanation:
a. in cursive writing as your signature
In a (Gallup poll, 26.6% of 5000 people reported a Body Mass Index (BMl) greater than 30, which is classified as obese. The 5000 people polled are a random sample of adults, aged 18 and older, from the United States population. Choose the correct interpretation for the 98% confidence interval for the proportion of the population who arc obese? A. The proportion of adults in the United States, aged 18 or older, who are obese is between 0.2515 and 0.2805. B. We are 98% confident the proportion of adults polled who are obese is between 0.2515 and 0.2805. C. In 98% of all samples, the proportion of adults polled who are obese will be between 0.2515 and 0.2805. D. We are 98% confident that the proportion of adults in the United States, aged 18 or older, who are obese is between 0.2515 and 0.2805.
Answers
Answer:
D. We are 98% confident that the proportion of adults in the United States, aged 18 or older, who are obese is between 0.2515 and 0.2805.
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the z-score that has a p-value of \(1 - \frac{\alpha}{2}\).
26.6% of 5000 people reported a Body Mass Index (BMl) greater than 30
This means that \(\pi = 0.266, n = 5000\)
98% confidence level
So \(\alpha = 0.02\), z is the value of Z that has a p-value of \(1 - \frac{0.02}{2} = 0.99\), so \(Z = 2.327\).
The lower limit of this interval is:
\(\pi - z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.266 - 2.327\sqrt{\frac{0.266*0.734}{5000}} = 0.2515\)
The upper limit of this interval is:
\(\pi - z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.266 + 2.327\sqrt{\frac{0.266*0.734}{5000}} = 0.2805\)
The correct interpreation is that we are 98% confident that the proportion of adults in the United States, aged 18 or older, who are obese is between 0.2515 and 0.2805, which means that the correct answer is given by option D.
Which Is The Simplified Rational Expression?

Answers
Answer:
1st choice
Step-by-step explanation:
(r² -4r + 5 - r² -2r + 8) / (r - 4)
= (-6r + 13) / (r - 4)
in symbolizing truth-functional claims, the word "if" used alone introduces the consequent of a condition. "only if" represents the antecedent.
Answers
In symbolizing truth-functional claims, the word "if" is used to introduce the consequent of a condition, while the phrase "only if" represents the antecedent.
Symbolizing truth-functional claims involves representing statements or propositions using logical symbols. When using the word "if" in a truth-functional claim, it typically introduces the consequent of a conditional statement. A conditional statement is a type of proposition that states that if one thing (the antecedent) is true, then another thing (the consequent) is also true. For example, the statement "If it is raining, then the ground is wet" can be symbolized as "p → q," where p represents "it is raining" and q represents "the ground is wet."
On the other hand, the phrase "only if" is used to represent the antecedent in a truth-functional claim. In a conditional statement using "only if," it states that if the consequent is true, then the antecedent must also be true. For example, the statement "The ground is wet only if it is raining" can be symbolized as "q → p," where p represents "it is raining" and q represents "the ground is wet."
In summary, when symbolizing truth-functional claims, the word "if" introduces the consequent of a condition, while the phrase "only if" represents the antecedent. These terms help express the relationships between propositions in logical statements.
Learn more about symbols here: https://brainly.com/question/30763849
#SPJ11
Weakly dependent and asymptotically uncorrelated time series Consider the sequence X; where (e ; t = 0,1,_is an i.d sequence with zero mean and constant variance of 0? True or False: This process is asymptotically uncorrelated
Answers
False. The given sequence X; where (e ; t = 0,1,... is an i.d sequence with zero mean and constant variance of σ^2, does not necessarily imply that the process is asymptotically uncorrelated.
The term "asymptotically uncorrelated" refers to the property where the autocovariance between observations of the time series tends to zero as the lag between the observations increases. In the given sequence, since the random variables e; are independent, the cross-covariance between different observations will indeed tend to zero as the lag increases. However, the process may still have non-zero autocovariance for individual observations, depending on the properties of the underlying random variables.
In order for the process to be asymptotically uncorrelated, not only should the cross-covariance tend to zero, but the autocovariance should also tend to zero. This would require additional assumptions about the distribution of the random variables e; beyond just being i.d with zero mean and constant variance.
Know more about constant variance here:
https://brainly.com/question/30281901
#SPJ11
pls help me, i’ll give brainliest

Answers
Answer:
the set of integers
Step-by-step explanation:
Arnetta's monthly gross pay is $4,568. federal withholding is 16.55% of her pay. her other deductions total $318.10. find her net pay. round to the nearest cent if necessary. her net pay is
Answers
Answer:
3493.90
Step-by-step explanation:
total = 100% = 4568
withholding = 16.55% of pay = 16.55% of 4568
1. convert 16.55% to a decimal by dividing by 100
16.55% = 0.1655
2. multiply that by the 100% number
0.1655 * 4568 = 756.004 = 16.55% of 4568
3. subtract that from the original
pay - federal withholding = 4568- 756.004 = 3811.996
then, subtract her other deductions from that amount
3811.996 - 318.10 = 3493.896 ≈ 3493.90
a daily mail is delivered to your house between 3:00 p.m. and 7:00 p.m. assume delivery times follow the continuous uniform distribution. determine the percentage of mail deliveries that are made after 6:00 p.m.
Answers
So, approximately 25% of mail deliveries are made after 6:00 p.m.
To determine the percentage of mail deliveries that are made after 6:00 p.m., we need to find the proportion of the continuous uniform distribution that lies between 6:00 p.m. and 7:00 p.m.
The total range of delivery times is 4 hours (from 3:00 p.m. to 7:00 p.m.), so the distribution has a uniform density of 1/4 over this range.
The proportion of deliveries made after 6:00 p.m. is the proportion of the area under the density curve that lies to the right of 6:00 p.m.
The area under the density curve from 3:00 p.m. to 6:00 p.m. is (6:00 - 3:00)/(7:00 - 3:00) = 3/4 of the total area.
Therefore, the proportion of deliveries made after 6:00 p.m. is (1 - 3/4) = 1/4, or 25%.
So, approximately 25% of mail deliveries are made after 6:00 p.m.
learn more about continuous uniform distribution
https://brainly.com/question/30893381
#SPJ11
Solve the equation
n/10+6=13
Answers
Answer:
n = 70
Step-by-step explanation:
n/10 + 6 = 13
n/10 = 7
n = 70
CHECK:
70/10 + 6 = 13
Write the equations in cylindrical coordinates. 5x2 - 9x + 5y2 + z2 = 5 (a) z = 2x2 – 2y? (b) (-9, 9/3, 6) (c)
Answers
The result (-9, 9/3, 6) has cylindrical coordinates (3√2, π/4, 6)
The equation is given by:5x² - 9x + 5y² + z² = 5
In cylindrical coordinates, x = r cosθ, y = r sinθ and z = z.
Substituting these into the equation we have:r²cos²θ - 9rcosθ + 5r²sin²θ + z² = 5r²(cos²θ + sin²θ) + z² = 5r² + z²
In cylindrical coordinates, the equation becomes:r² + z² = 5 ------------(1)
The equation of the cylinder in cylindrical coordinates is obtained as follows:r² = x² + y²
From the given equation, we have:r² = x² + y² = 5 - z²r² + z² = 5 ------------(2)
Comparing (1) and (2) we have:r² = 5 - z² and z = 2x² - 2y
Substituting the value of z in terms of x and y into (2), we have:r² = 5 - (2x² - 2y)² = 5 - 4x⁴ + 8x²y² - 4y⁴
Now we can write the equations in cylindrical coordinates as follows:
a. z = 2x² - 2y becomes z = 2r²cos²θ - 2r²sin²θ which is simplified to z = r²(cos²θ - sin²θ)b.
(-9, 9/3, 6) has cylindrical coordinates (3√2, π/4, 6)
Know more about the cylindrical coordinates
https://brainly.com/question/31400636
#SPJ11
1. The cost of buying some books is partly constant and partly varies with the number of books bought. The cost is #4800 when 20 books are bought and #8000 when 40 are bought. Find the cost when 1000 books are bought
Answers
Answer:
Step-by-step explanation:
let the cost based on number of book bought be x and the constant be c:
4800 = 20x + c
8000 = 40x + c
c is common in both equations:
c =4800-20x
c = 8000-40x
equate the two:
4800-20x = 8000 - 40x
20x = 3200
x = 160
and c = 4800-20*160
c = 1600
Cost of 1000 books:
160*1000 + 1600
= 161600