Ellason wants to solve the following system using the elimination method:
5x + 2y = 30
x + y = 8
What number should the equation x + y = 8 be multiplied by to eliminate y? (4 points)
Answers
Related Questions
What is the probability that a standard normal random variable will be between 0.3 and 3.2?
Answers
A standard normal random variable has a 0.3814 percent chance of falling between 0.3 and 3.2, according to the z table.
What is probability?The probability is calculated by dividing the total number of outcomes by the total number of events.
Odds and probability are two different concepts.
Divide the probability of an event occurring by the probability that it won't happen to calculate chances.
The four main types of probability that mathematicians study are axiomatic, classical, empirical, and subjective.
So, the probability that a standard normal random variable will occur with a probability ranging from 0.3 to 3.2 must therefore be calculated.
First, a mean and standard deviation are introduced for a standard normal random variable.
The probability that a standard normal random variable will fall between 0.3 and 3.2 needs to be calculated.
Therefore, it should be more likely that:
P(0.3<z<3.2)=P(z<3.2)−P(z<0.3)
Using the usual value of z:
P(0.3<z<3.2)=0.9993−0.6179
Justify by saying:
P(0.3<z<3.2)=0.3814
Therefore, a standard normal random variable has a 0.3814 percent chance of falling between 0.3 and 3.2, according to the z table.
Know more about probability here:
brainly.com/question/24756209
#SPJ4
Name the smallest angle of angle ABC the diagram is not scale.
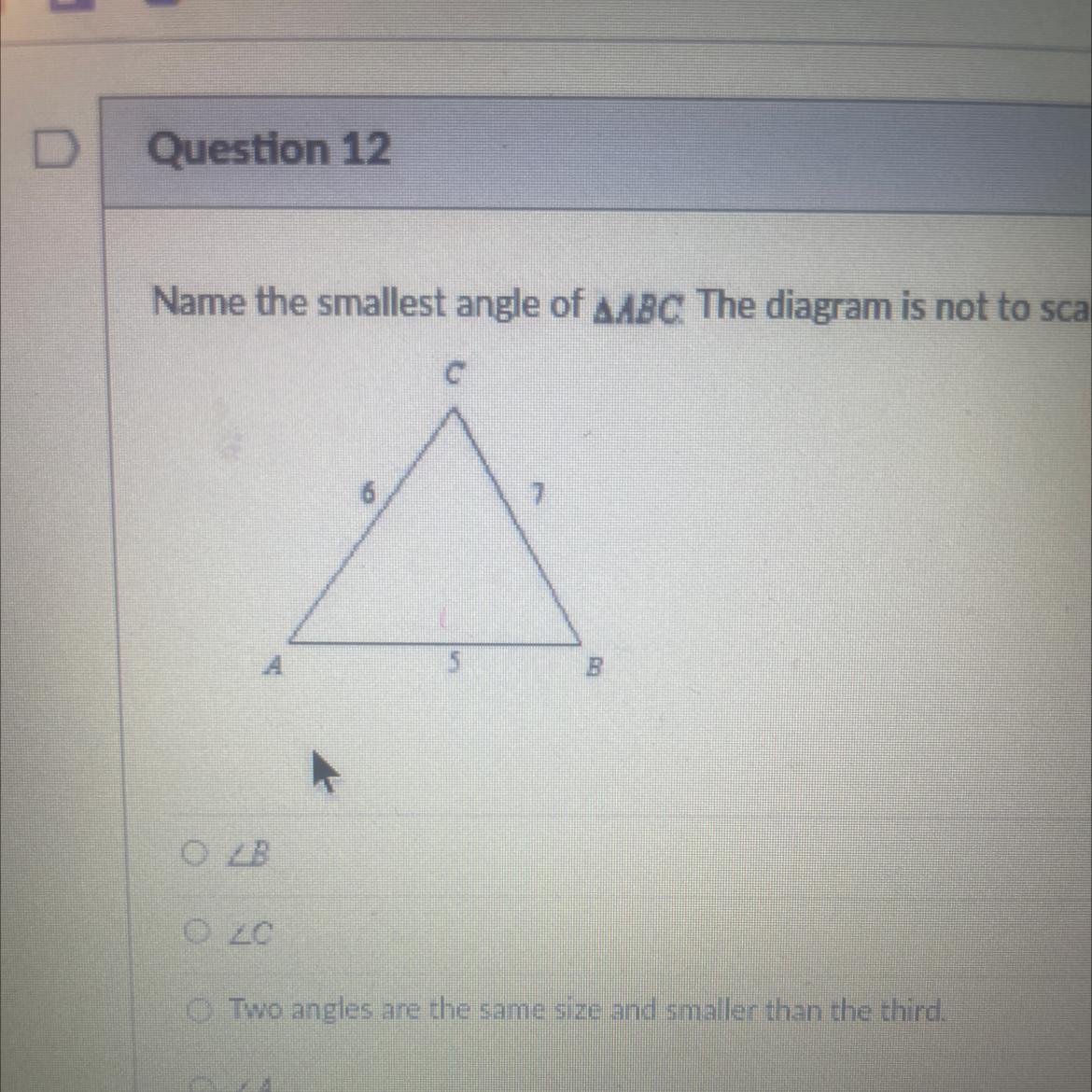
Answers
The angle is none because all angles are 60
So far, Yoko has burned 773.5 calories. She wants to burn a total of 800 calories. How many more calories must Yoko burn?
Answers
Answer:
Yoko must burn 26.5 more calories.
Step-by-step explanation:
You have to take how many calories she wants to burn and subtract how many she already has burned. In this case, it would be 800-773.5. This equals 26.5, so 26.5 is your answer.
Hope this helps,
noah
help plsssssssssssss

Answers
Answer:
85,000 and 90,000
Step-by-step explanation:
I need help with this geometry equation

Answers
The area of the composite figure is 58. 71 square units.
How to determine the areaIt is important to note that the area of the composite figure is given as;
Area of a rectangle + area of a semi circle
The formula for area of a rectangle is expressed as;
Area = lw
Where;
l is the length of the rectanglew is the width of the rectangleNow, let's substitute the values, we have;
Area = 6 × 9
Area = 54 square units
The formula for area of a semicircle is expressed as;
Area = πr²/2
Where;
pi = 3. 14r is the radius of the semi circleGiven diameter = 6, radius = 6/2 = 3
Substitute the value
Area = 3. 14(3)/2
Area = 4. 71 square units
But area of the composite figure = 54 + 4. 71 = 58. 71 square units.
Hence, the area is 58. 71 square units.
Learn more about area here:
https://brainly.com/question/25292087
#SPJ1
The point P(x, y) is on the terminal ray of angle theta. If theta is between pi and 3pi/2 radians and csc theta equals -5/2 what are the coordinates of P(x, y)?
Answers
Answer:
(-4.58, -2)
Step-by-step explanation:
\(\theta $ is in between \pi$ and $\frac{3\pi}{2}$ radians \\Therefore, \theta$ is in Quadrant III\\If \csc \theta = -\dfrac{5}{2}$ and cosec \theta = \dfrac{Hypotenuse}{Opposite} \\ $Therefore:\\Hypotenuse = 5\\Opposite $=-2\)
Using Pythagoras Theorem
\(5^2=(-2)^2+ x^2\\25=4+x^2\\x^2=21\\x=\sqrt{21} \approx 4.58\)
Since the angle is in the third Quadrant, Adjacent = -4.58.
Therefore, the coordinates of P(x,y) is (-4.58, -2)
Answer: a
Step-by-step explanation: edge 2021
Hint(s) A population has a mean of 300 and a standard deviation of 70. Suppose a simple random sample of size 125 is selected and I is used to estimate H. Use z-table. a. What is the probability that the sample mean will be within 29 of the population mean (to 4 decimals)? b. What is the probability that the sample mean will be within 16 of the population mean (to 4 decimals)? Hint(s) 0 Icon Key
Answers
a. To calculate the probability that the sample mean will be within 29 of the population mean, use the standard error formula and the z-score formula to find the cumulative probability between the z-scores corresponding to -29/SE and 29/SE.
b. Similarly, calculate the probability that the sample mean will be within 16 of the population mean using the same approach.
a. To calculate the probability that the sample mean will be within 29 of the population mean, we can use the standard normal distribution and the formula for the standard error of the mean. The standard error of the mean (SE) is calculated as the standard deviation of the population divided by the square root of the sample size.
SE = standard deviation / √sample size
= 70 / √125
≈ 6.244997998
To find the probability, we can use the z-score formula:
z = (sample mean - population mean) / SE
For a sample mean within 29 of the population mean, we need to calculate the probability of getting a z-score between -29/SE and 29/SE.
Using a z-table or a calculator, we can find the corresponding probabilities for the z-scores. Subtracting the cumulative probability for the negative z-score from the cumulative probability for the positive z-score will give us the desired probability.
b. Similarly, to calculate the probability that the sample mean will be within 16 of the population mean, we follow the same steps as above, but with a different range of z-scores.
It's important to note that the z-table may provide probabilities for z-scores up to a certain decimal place. To achieve the desired precision, it's necessary to consult a more detailed z-table or use a calculator that provides more decimal places.
Learn more about probability here:-
https://brainly.com/question/14740947
#SPJ11
33, 25, 42, 25, 31, 37, 46, 29, 38 what is the interquartile range of the data?
Answers
The interquartile range of the data will be 13
When arranged from lowest to highest, the IQR reflects the median 50% of values. To calculate the interquartile range (IQR), firstly compute the median (middle value) of the data's lower and upper halves. All those are quartile 1 (Q1) and quartile 3 (Q3) values (Q3). The interquartile range is the difference between quarters three and then one.
first, let us sort the data from lowest to highest
25,25,29,31,33,37,38,42,46
Q1- median of the lower half of the data=(29+25)/2=27
Q3-median of the upper half of the data=(38+42)/2=40
the interquartile range of the data will be Q3-Q1
40-27= 13
Learn more about interquartile range here:https://brainly.com/question/17083142
#SPJ4
Sophia owns a small business selling used books. She knows that in the last week 15 customers paid cash, 50 customers used a debit card, and 15 customers used a credit card. Based on these results, express the probability that the next customer will pay with a debit card as a decimal to the nearest hundredth.
Answers
The probability that the next person will pay with a debit card is:
P = 0.63
How to find the probability?
We want to find he probability that the next customer will pay with a debit card.
That probability can be estimated as the quotient between the number of customers that paid with debit card and the total number of customers.
We know that:
15 paid in cash.
50 paid with debit card.
15 paid with credit card.
For a total of 15 + 50 + 15 = 80
Then the probability is:
P = 50/80 = 0.63
Learn more about probability at:
https://brainly.com/question/25870256
#SPJ1
Find the volume of the solid enclosed by the paraboloid z = 2 + x2 + (y - 2)2 and the planes z = 1, x = ?2, x = 2, y = 0, and y = 3.
Answers
Main Answer:The volume of the solid enclosed by the paraboloid and the planes is 18.67 cubic units.
Supporting Question and Answer:
How do we calculate the volume of a solid bounded by surfaces using triple integration?
To calculate the volume of a solid bounded by surfaces using triple integration, we set up a triple integral with the integrand equal to 1, representing the infinitesimal volume element. The bounds of integration are determined by the equations defining the surfaces that enclose the solid. By evaluating the triple integral over the specified region, we can find the volume of the solid.
Body of the Solution: To find the volume of the solid enclosed by the paraboloid z = 2 + x^2 + (y - 2)^2 and the planes z = 1, x = -2, x = 2, y = 0, and y = 3, we can set up a triple integral in the given region.
To find the volume,using the triple integral:
V = ∫∫∫ R (1) dz dy dx
where R is the region bounded by the given planes and the paraboloid.
The bounds of integration for x are -2 to 2, for y are 0 to 3, and for z are the lower bound function z = 1 and the upper bound function z = 2 + x^2 + (y - 2)^2.
Setting up the triple integral:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 ∫ from z = 1 to 2 + x^2 + (y - 2)^2 (1) dz dy dx
Integrating the innermost integral with respect to z:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 [(2 + x^2 + (y - 2)^2) - 1] dy dx
Simplifying the expression inside the integral:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 [x^2 + (y - 2)^2 + 1] dy dx
Integrating the inner integral with respect to y:
V = ∫ from x = -2 to 2 [x^2(y) + ((y - 2)^3)/3 + y] evaluated from y = 0 to 3 dx
Substituting the limits of integration for y:
V = ∫ from x = -2 to 2 [x^2(3) + (3 - 2)^3/3 + 3 - (x^2(0) + (0 - 2)^3/3 + 0)] dx
Simplifying further:
V = ∫ from x = -2 to 2 [3x^2 +2/3] dx
Integrating the final integral with respect to x:
V = [(x^3) + (2/3)x] evaluated from x = -2 to 2
Evaluating the expression at the limits:
V = [(2^3) +(2/3) 2] - [((-2)^3) + (2/3)(-2)]
V = (8 +4/3) - (-8 - 4/3)
V = 16+8/3
V =56/3
Final Answer:Therefore, the volume of the solid enclosed by the paraboloid and the given planes is 56/3 cubic units.
To learn more about the volume of a solid bounded by surfaces using triple integration from the given link
https://brainly.com/question/31473156
#SPJ4
The volume of the solid enclosed by the paraboloid and the planes is 18.67 cubic units.
How do we calculate the volume of a solid bounded by surfaces using triple integration?To calculate the volume of a solid bounded by surfaces using triple integration, we set up a triple integral with the integrand equal to 1, representing the infinitesimal volume element. The bounds of integration are determined by the equations defining the surfaces that enclose the solid. By evaluating the triple integral over the specified region, we can find the volume of the solid.
Body of the Solution: To find the volume of the solid enclosed by the paraboloid z = 2 + x^2 + (y - 2)^2 and the planes z = 1, x = -2, x = 2, y = 0, and y = 3, we can set up a triple integral in the given region.
To find the volume,using the triple integral:
V = ∫∫∫ R (1) dz dy dx
where R is the region bounded by the given planes and the paraboloid.
The bounds of integration for x are -2 to 2, for y are 0 to 3, and for z are the lower bound function z = 1 and the upper bound function z = 2 + x^2 + (y - 2)^2.
Setting up the triple integral:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 ∫ from z = 1 to 2 + x^2 + (y - 2)^2 (1) dz dy dx
Integrating the innermost integral with respect to z:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 [(2 + x^2 + (y - 2)^2) - 1] dy dx
Simplifying the expression inside the integral:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 [x^2 + (y - 2)^2 + 1] dy dx
Integrating the inner integral with respect to y:
V = ∫ from x = -2 to 2 [x^2(y) + ((y - 2)^3)/3 + y] evaluated from y = 0 to 3 dx
Substituting the limits of integration for y:
V = ∫ from x = -2 to 2 [x^2(3) + (3 - 2)^3/3 + 3 - (x^2(0) + (0 - 2)^3/3 + 0)] dx
Simplifying further:
V = ∫ from x = -2 to 2 [3x^2 +2/3] dx
Integrating the final integral with respect to x:
V = [(x^3) + (2/3)x] evaluated from x = -2 to 2
Evaluating the expression at the limits:
V = [(2^3) +(2/3) 2] - [((-2)^3) + (2/3)(-2)]
V = (8 +4/3) - (-8 - 4/3)
V = 16+8/3
V =56/3
Therefore, the volume of the solid enclosed by the paraboloid and the given planes is 56/3 cubic units.
To learn more about the volume of a solid
brainly.com/question/31473156
#SPJ4
the length of a retangle multiplied by 3 is equal to 4 times the width. the perimeter is 8(2)/(5)feet. find the length and width
Answers
The answer is that the length and the width of the rectangle are respectively are 32/35 feet and 24/35 feet.
This question is based on the perimeter of the rectangle .
Now, here let the length and the breadth of the rectangle be l and b respectively.
So, According to question , 3l=4b or b = 3l/4 .... (i)
Also, the perimeter is given as 16/5 feet. We know that the perimeter of a rectangle is 2(l+b) .
So, 16/5= 2(l+b)
= 2(l+3l/4)
= 2(7l/4).
From here, l comes out to be 32/35 feet.
Putting this value in (i) , we get b = 24/35 feet.
So, the length and the width of the rectangle are respectively are 32/35 feet and 24/35 feet.
To learn more about perimeter , visit link - brainly.com/question/29595517
#SPJ4
How do you solve quotients step by step?
Answers
We can Long Division method to solve quotients step by step
What is long division method and its steps ?
When splitting huge numbers, the task is divided into several sequential parts using the long division approach. The dividend is divided by the divisor, just as in conventional division problems, and the result is known as the quotient; occasionally, it also produces a remainder.
We need to comprehend a few stages in order to divide. A vinculum or right parenthesis separates the dividend from the quotient, while a vertical bar separates the divisor from the dividend. Let's now go through the long division stages listed below to comprehend the procedure.
1. Take the dividend's first digit starting from the left . Verify if this digit exceeds or is equal to the divisor.
2. Next, divide it by the divisor, and write the result as the quotient on top.
3. Subtract the outcome from the digit, and then put the difference below.
Step 4: Decrease the dividend's subsequent digit (if present).
Step 5: Carry out Step 4 again.
Learn more about Long division from the link below
https://brainly.com/question/28824872
#SPJ4
____A mail clerk is making deliveries along a long straight hallway. The clerk's velocity is modeled in meters/min by v(t) = 4π sin(). If the clerk starts at one end and takes 13 minutes to finish deliveries, how many 3 meters did the clerk walk during the132 minutes?
Answers
The clerk walked approximately 0.371π meters during the 132 minutes of delivering along the hallway.
To find the number of 3-meter segments the clerk walked during the 132 minutes, we need to integrate the velocity function over the given time interval.
v(t) = 4π sin(t)
The clerk starts at one end and takes 13 minutes to finish deliveries, so the time interval is from t = 0 to t = 13.
To calculate the distance walked, we integrate the absolute value of the velocity function over the given interval:
Distance = ∫[0, 13] |v(t)| dt
Let's calculate the integral:
Distance = ∫[0, 13] |4π sin(t)| dt
Since the absolute value of sin(t) is positive for the given interval, we can simplify the integral to:
Distance = 4π ∫[0, 13] sin(t) dt
Using the integral of sin(t), which is -cos(t), the expression becomes:
Distance = -4π cos(t) |[0, 13]
Now we can evaluate the integral over the given interval:
Distance = -4π (cos(13) - cos(0))
Simplifying further:
Distance = -4π (cos(13) - 1)
Calculating the value:
Distance ≈ -4π (0.907 - 1)
Distance ≈ -4π (-0.093)
Distance ≈ 0.371π meters
Therefore, the clerk walked approximately 0.371π meters during the 132 minutes.
To learn more about velocity function visit : https://brainly.com/question/25749514
#SPJ11
plss help me!!
A navy ship observes an illigal boat 'd' miles away to it's West. If the boat travels at a 'u' velocity towards the south , and it's given that the maximum velocity of the ship's canon is λu ( λ<1)
and the max range they can be shot at is 'v',
show that if λ^2 +(v/d)^2 <1 ,
1) that the illigal boat can avoid any harm caused by the navy ship.
( use relative velocity triangles and geometry)
Answers
Step-by-step explanation:
The problem statement says λ<1. If this is true, then the cannonball is slower than the boat, and it will never reach the boat. So I assume it's actually λ>1.
If we say t is the amount of time, then the boat travels south a distance of ut, and the cannonball travels a distance of λut.
v = λut
ut = v/λ
Using Pythagorean theorem:
d² + (ut)² > v²
d² + (v/λ)² > v²
λ²d² + v² > λ²v²
λ²d² > (λ² − 1) v²
λ² / (λ² − 1) > (v/d)²

(This question may have more than one solution.) Let C be a fixed n × n matrix. Determine whether the following are linear
operators on R^X":
(a) L(A) = 1 - 1
(6) L(A) = 1 + 17
(c) L(1) = C1 + AC
(d) L(1) = C°1
(c) L(1) = 1?C
Answers
Functions (c) L(1) = C1 + AC and (d) L(1) = C°1 are linear operators on R^n, while functions (a), (b), and (e) do not satisfy the properties of linearity and therefore are not linear operators.
a) L(A) = 1 - 1: This function is not a linear operator because it does not preserve scalar multiplication. Multiplying A by a scalar c would yield L(cA) = c - c, which is not equal to cL(A) = c(1 - 1) = 0.
b) L(A) = 1 + 17: Similar to the previous case, this function is not linear since it fails to preserve scalar multiplication. Multiplying A by a scalar c would result in L(cA) = c + 17, which is not equal to cL(A) = c(1 + 17) = c + 17c.
c) L(1) = C1 + AC: This function is a linear operator since it satisfies both the preservation of addition and scalar multiplication properties. Adding matrices A and B and multiplying the result by scalar c will yield L(A + B) = C(1) + AC + C(1) + BC = L(A) + L(B), and L(cA) = C(1) + cAC = cL(A).
d) L(1) = C°1: This function is a linear operator since it satisfies the properties of linearity. Addition and scalar multiplication are preserved, and L(cA) = C(0)1 = c(C(0)1) = cL(A).
e) L(1) = 1?C: This function is not a linear operator as it does not preserve scalar multiplication. Multiplying A by a scalar c would give L(cA) = 1?(cC), which is not equal to cL(A) = c(1?C).
In summary, functions (c) L(1) = C1 + AC and (d) L(1) = C°1 are linear operators on R^n, while functions (a), (b), and (e) do not satisfy the properties of linearity and therefore are not linear operators.
Learn more about scalar multiplication here:
https://brainly.com/question/28875206
#SPJ11
When u and v are nonzero vectors, Spanlu,v) contains only the line through u and the line through v and the origin. OA. False. Span(u,v) includes linear combinations of both u and v. 0 B. False. Span(u,v) will not contain the origin. ° C. True. Span(u,v) is the set of all scalar multiples of u and all scalar multiples of v
Answers
False. Span(u,v) includes linear combinations of both u and v.
The correct option is A
Now, According to the question:
When u and v are nonzero vectors, Span {u, v} contains only the line through u and the origin, and the line through v and the origin. b. Any list of five real numbers is a vector in ℝ5 .
Span(u,v) is the set of all linear combinations of u and v, meaning any combination of u and v multiplied by scalars. This includes scalar multiples of both u and v, but does not include the origin. To calculate Span(u,v), first write u and v as vectors u = (u1,u2,...,un) and v = (v1,v2,...,vn). Then, any linear combination of u and v can be written as c1u + c2v, where c1 and c2 are scalars, and the set of all such linear combinations is Span(u,v). For example, if u = (1,2) and v = (3,4), then Span(u,v) = {(1,2), (3,4), (4,6), (5,8), (7,10), ...}. In other words, Span(u,v) is the set of all scalar multiples of u and all scalar multiples of v.
Learn more about linear combinations at:
https://brainly.com/question/29551145
#SPJ4
The equation of the line of best fit is y = 0.677x + 1.77.
Based on the line of best fit, approximately how many students are predicted to be in the marching band at a school with 35 students in the concert band?
Answers
There are 25 students in the marching band
How to determine the number of students?The equation of the line of best fit is
y = 0.677x + 1.77
The number of students in the concert band is given as
Students =35
This means that
x = 35
Substitute 35 for x in the equation y = 0.677x + 1.77
So, we have
y = 0.677 x 35 + 1.77
Evaluate the products in the above equation
This gives
y = 23.695+ 1.77
Add the numbers
y = 25.465
Approximate
y = 25
Hence, the students are 25
Read more about linear regression at
https://brainly.com/question/10209928
#SPJ1
Find the x,y,z
For 10points

Answers
Answer:
x = y = 110°z = 70°Step-by-step explanation:
You want to know angles x, y, and z in the given figure where parallel lines 'a' and 'b' are crossed by a transversal. The sum of these angles is 290°.
Consecutive interior anglesAngles y and z are called consecutive interior angles. As such, they are supplementary, so their sum is 180°.
x + y + z = 290°
x + 180° = 290°
x = 110°
Vertical anglesAngles x and y are vertical angles, so are congruent.
y = x = 110°
Then z is found from ...
y + z = 180°
110° + z = 180°
z = 70°
The measures of x, y, and z are 110°, 110°, and 70°, respectively.
<95141404393>
Rewrite the equation in Ax+BY =C form please and thank you

Answers
Answer:
3x - y = 20
Step-by-step explanation:
First, distribute the 3 among everything within the parentheses to get
y + 2 = 3x - 18.
Next, add 18 on both sides to get
y + 20 = 3x.
Now subtract y on both sides in order to move it.
Your answer is now: 20 = 3x - y, or
3x - y = 20.
Hope this helps :)
I need help with this asap (50 Points)

Answers
Answer:
Multiply this measurement by two to account for both sides. Add the three separate measurements together. Because surface area is the total area of all of the faces of an object, the final step is to add all of the individually calculated areas together.
Step-by-step explanation:
PLZ HURRY I ONLY HAVE 27 MINUTES TO GET THIS DONE
The owner of a local music store was interested in knowing which type of music most of his customers preferred. From a list of his regular customers the owner picked a name at random and every sixth person on the list after that, going through the list and returning to the name he started with. Was this a random sample and if so, which sampling method was used? A. Yes, he used simple random sampling. B. Yes, he used systematic random sampling. C. Yes, he used stratified random sampling. D. No, he did not choose a random sample.
Answers
Answer:
definitely b.
Step-by-step explanation:
Answer:
I'm just going with the person above me that the answer is B. Yes, he used systematic random sampling.
Step-by-step explanation:
Tell me if I'm wrong.
Use the x-coordinates A and C to calculate AC without counting
Answers
W+15x-9y+2z
Terms:
Coefficients:
Answers
In the problem given:
W + 15x - 9y + 2z
The term are single mathematical expressions that separate values.
In the expression, there is a + and -; these concludes 2 terms.
There are 3 coefficients next to each variable.
The coefficients are 15x, -9y, and 2z.
That means there are 3 coefficients.
Cheers
- ROR
\(\quad \huge \quad \quad \boxed{ \tt \:Answer }\)
\( \sf{W \rightarrow coefficient = 1} \)\( \sf{15x \rightarrow coefficient = 15} \)\( \sf{-9y\rightarrow coefficient = -9} \)\( \sf{2z\rightarrow coefficient = 2} \)
____________________________________
\( \large \tt Solution \: : \)
Term refers to each variable or constant separated by a mathematical operator.
Coefficient refers to the numberic part of variable or a constant number present in an expression.
\(\qquad \tt \rightarrow \: 12a - 10b + 6\)
\( \large\textsf{Terms :} \)
\( \texttt{W } \)\( \texttt{coefficient = 1} \)
\( \texttt{15x} \)\( \texttt{coefficient = 15} \)
\( \texttt{-9y} \)\( \texttt{coefficient = -9} \)
\( \texttt{ 2z} \)\( \texttt{coefficient= 2} \)
Answered by : ❝ AǫᴜᴀWɪᴢ ❞
please help...
thanks due in some hours

Answers
Answer:
1. x=4 y=4√3
2. x=48 y=24√3
4. x=7/√3 y= 14/√3
5. x=27√3 y = 54
Step-by-step explanation:
Find the length of the third side. If necessary, round to the nearest tenth

Answers
Answer: To find the length of the third side, we need to find the length of the hypotenuse. The hypotenuse is 8 + 10 = 18. So the length of the third side is 18.
Step-by-step explanation:
How many solutions?
2x + 6 = 3(x + 2) - x
Answers
Answer:
2x = 2x
Step-by-step explanation:
2x + 6 = 3x + 6 - x
2x = 3x - x(cancel equal terms)
2x=2x
a dessert chef prepares the dessert for every day of a week starting with sunday. the dessert each day is either cake, pie, ice cream, or pudding. the same dessert may not be served two days in a row. there must be cake on friday because of a birthday. how many different dessert menus for the week are possible?
Answers
There are 324 different dessert menus possible for the week, considering the restriction that there must be cake on Friday and no dessert can be repeated two days in a row.
To determine the number of different dessert menus for the week, we can approach the problem systematically.
Since there are four options for dessert each day (cake, pie, ice cream, or pudding), and the same dessert may not be served two days in a row, we need to consider the dessert choices for each day of the week.
Let's start with the restriction that there must be cake on Friday due to a birthday. We have three options for dessert on the other six days (excluding Friday) because we cannot repeat the dessert from the previous day.
To count the number of dessert menus, we can consider the choices for each day of the week starting from Sunday:
1. Sunday: There are four options for dessert since no dessert has been served yet.
2. Monday: There are three options left since we cannot repeat Sunday's dessert.
3. Tuesday: There are three options available, excluding Monday's dessert.
4. Wednesday: There are three options remaining, excluding Tuesday's dessert.
5. Thursday: There are three options available, excluding Wednesday's dessert.
6. Friday: There must be cake, so only one option is available.
To find the total number of dessert menus, we multiply the number of options for each day:
4 options × 3 options × 3 options × 3 options × 3 options × 1 option = 324 dessert menus
Therefore, there are 324 different dessert menus possible for the week, considering the restriction that there must be cake on Friday and no dessert can be repeated two days in a row.
Each dessert menu represents a unique combination of desserts for each day of the week, satisfying the given conditions.
In conclusion, the dessert chef has 324 different dessert menu options for the week, ensuring a variety of desserts and fulfilling the requirement of having cake on Friday.
Learn more about restriction here
https://brainly.com/question/28368825
#SPJ11
please help asap I will give brainliest :-)

Answers
Step-by-step explanation:
60°+x=2x+4
56°=x
m (2x+4)=2 (56)+4
=116°
I do believe i need help.

Answers
Answer:
A
Step-by-step explanation:
Can't have 0 in the denominator
1. So far this month Raul calculated that he will ear $40 in commission for his
$280 in product sales. If Raul would like for his commission to be $132, how much
does her need in sales? *
Answers
Answer:
Raul needs sales of $924.
Step-by-step explanation:
It looks like Raul earns commission at 1/7 of his sales. (40/280 = 1/7).
\(\frac{40}{280}=\frac{132}{x}\\ 40x = 280*132\\x=924\)