Elijah has $1.60 worth of nickels and dimes. He has 5 more nickels than dimes. Determine the number of nickels and the number of dimes that Elijah has.
Answers
Number of nickels = 14
Number of dimes = 9
Let n= number of nickels
Let d = number of dimes
Given:
n = d + 5 ---1---
160 = 5n +10d ----2---
Substitute (1) in (2)
160 = 5d + 25 + 10d
15d = 135
d = 9
n = 14
Hence,
Number of nickels = 14
Number of dimes = 9
Learn more about nickels and dimes from the link
https://brainly.com/question/28793265
#SPJ1
Related Questions
write an equation in slope-intercept form for the line that passes through (9,12) and is parallel to y=4
Answers
An equation in slope-intercept form for the line that passes through (9,12) and is parallel to y=4 is y= 4x -24.
What is Parallel lines?
Parallel lines in geometry are coplanar, straight lines that don't cross at any point. In the same three-dimensional space, parallel planes are any planes that never cross. Curves with a predetermined minimum distance between them and no contact or intersection are said to be parallel.
Parallel lines will have the same slope but different y-intercepts so again we can use the coordinates to determine the y intercept of the new equation.
So we know that the slope intercept formula is y=mx + b where m is the slope and b is the y-intercept so we will input the x and y coordinates to solve for b.
12 = 4(9) + b
12 = 36 + b
b = -24
The equation will be y= 4x -24.
To learn more about Parallel lines visit:https://brainly.com/question/16701300
#SPJ1
If h = 8.1 inches and k = 9 inches, what is the approximate measure of angle α?
Answers
Answer:
brainliest please, i need it and it takes one click
Answer: C. 26°
Step-by-step explanation:
Right triangle: a triangle in which one of the interior angles measures 90°.
This type of angle can be solved using trigonometrical functions. As the measure of the sides given are h and k, then we will use:
In our case, it would be:
cosa = adjacent/hypotenuse
Replacing the values:
cosa = h/k
Solving for a:
cosa-1(cosa) = cos-1(8.1/9)
a = cos-1(8.1/9)
a≈ 25.8 ≈26
Answer: C. 26°
Pls help I need help
Hehhehrhrh

Answers
Answer:
C) 11.4
Step-by-step explanation:
Luisa began walking up a hill at a spot where the elevation is 0.9 km. After she walked
3 km, she saw a sign giving the elevation as 0.95 km. How far will she have walked when she
reaches and elevation of 1.1 km?
Answers
Answer:
3.82 km
Step-by-step explanation:
Assuming that the change in elevation is linear, we can calculate the elevation change per km traveled. The known values are the start (0km) and the sign (3km). The elevation gain over that interval is (0.95-9.0)km = 0.5km. That was for an distance interval of 3km, so we can write:
(0.5km elevation gain)/(3km distance)
We can use this as a rate change and and use it in a linear equation to predict the elevation as a function of distance.
Let y be the elevation and x the distance, both in km.
y = (0.183)(x)+b, where b is the elevation at the start of the trail. We can find b by using this equation and entering one of the two data points. Lets use the elevation of 0.95m at 3km distance:
y = (0.183)(x)+b
0.95 = (0.183)(3)+b
b = 0.4km
The full equation is :
y = (0.1833)X + 0.4
Enter 1.1 km for y and calculate x, the distance to reach 1.1 km altitude.
1.1 = (0.1833)X + 0.4
X = 3.82 km
-19 + m > 36
(The greater than sign has a line under it btw)
Answers
Answer:
m> 55 (you only flip the direction of the sign when you divide by a negative number)
Step-by-step explanation:
Answer:
m > 55
Step-by-step explanation:
simplify both sides of the inequality
m - 19 > 36
Add 19 to both sides
36+19
m>55
Hope this helps :D
Sorry the quality is bad- I’ll mark brainlist

Answers
Answer: A and C
Step-by-step explanation:
Consider the following rational expression: 4y + 16 y+ 4 Step 2 of 2: Find the restricted values of y, if any, for the given rational expression Answer How to enter your answer (opens in new window) 2
Answers
The given rational expression is 4y + 16 y + 4. To find the restricted values of y, we need to identify any values of y that would make the expression undefined.
In this case, the expression is in the form of a sum, so we don't have any denominators that could lead to division by zero. Therefore, there are no restricted values of y for this rational expression.
The expression 4y + 16 y + 4 is defined for all real numbers. We can evaluate it for any value of y without encountering any restrictions.
Learn more about rational expression here: brainly.com/question/25292194
#SPJ11
A car rental company charges a daily rate of $ 24 plus $ 0.10 per mile for a certain car. Suppose that you rent that car for a day and your bill (before taxes) is $ 37.00. How many miles did you drive?
_________miles
Answers
Explanation: make an equation. 24 + 0.10m = 37.00. subtract 24 from both sides leaving m for miles on one side. 0.10m = 13.00. now divide both sides by 0.10 leaving m by itself and making the equation m = 130.
explain how to solve 3x − 4 = 6 using the change of base formula . include the solution for x in your answer. round your answer to the nearest thousandth.
Answers
To solve 3x − 4 = 6 using the change of base formula, we first isolate the variable by adding 4 to both sides of the equation.
The given equation is 3x − 4 = 6. To solve for x, we want to isolate the variable on one side of the equation.
Step 1: Add 4 to both sides of the equation:
3x − 4 + 4 = 6 + 4
3x = 10
Step 2: Apply the change of base formula, which states that log(base b)(x) = log(base a)(x) / log(base a)(b), where a and b are positive numbers not equal to 1.
In this case, we will use the natural logarithm (ln) as the base:
ln(3x) = ln(10)
Step 3: Solve for x by dividing both sides of the equation by ln(3):
(1/ln(3)) * ln(3x) = (1/ln(3)) * ln(10)
x = ln(10) / ln(3)
Using a calculator, we can approximate the value of x to the nearest thousandth:
x ≈ 1.660
Therefore, the solution for x in the equation 3x − 4 = 6, using the change of base formula, is approximately x ≈ 1.660.
To learn more about nearest thousandth.
brainly.com/question/30284475
#SPJ11
Solve dy/dx=1/3(sin x − xy^2), y(0)=5
Answers
The general solution to the differential equation dy/dx = 1/3(sin x − xy^2), y(0)=5 is: y = ±√[(sin x - e^(x/2)/25)/x], if sin x - xy^2 > 0 and y(0) = 5
To solve this differential equation, we can use separation of variables.
First, we can rearrange the equation to get dy/dx on one side and the rest on the other side:
dy/dx = 1/3(sin x − xy^2)
dy/(sin x - xy^2) = dx/3
Now we can integrate both sides:
∫dy/(sin x - xy^2) = ∫dx/3
To integrate the left side, we can use substitution. Let u = xy^2, then du/dx = y^2 + 2xy(dy/dx). Substituting these expressions into the left side gives:
∫dy/(sin x - xy^2) = ∫du/(sin x - u)
= -1/2∫d(cos x - u/sin x)
= -1/2 ln|sin x - xy^2| + C1
For the right side, we simply integrate with respect to x:
∫dx/3 = x/3 + C2
Putting these together, we get:
-1/2 ln|sin x - xy^2| = x/3 + C
To solve for y, we can exponentiate both sides:
|sin x - xy^2|^-1/2 = e^(2C/3 - x/3)
|sin x - xy^2| = 1/e^(2C/3 - x/3)
Since the absolute value of sin x - xy^2 can be either positive or negative, we need to consider both cases.
Case 1: sin x - xy^2 > 0
In this case, we have:
sin x - xy^2 = 1/e^(2C/3 - x/3)
Solving for y, we get:
y = ±√[(sin x - 1/e^(2C/3 - x/3))/x]
Note that the initial condition y(0) = 5 only applies to the positive square root. We can use this condition to solve for C:
y(0) = √(sin 0 - 1/e^(2C/3)) = √(0 - 1/e^(2C/3)) = 5
Squaring both sides and solving for C, we get:
C = 3/2 ln(1/25)
Putting this value of C back into the expression for y, we get:
y = √[(sin x - e^(x/2)/25)/x]
Case 2: sin x - xy^2 < 0
In this case, we have:
- sin x + xy^2 = 1/e^(2C/3 - x/3)
Solving for y, we get:
y = ±√[(e^(2C/3 - x/3) - sin x)/x]
Again, using the initial condition y(0) = 5 and solving for C, we get:
C = 3/2 ln(1/25) + 2/3 ln(5)
Putting this value of C back into the expression for y, we get:
y = -√[(e^(2/3 ln 5 - x/3) - sin x)/x]
So the general solution to the differential equation dy/dx = 1/3(sin x − xy^2), y(0)=5 is:
y = ±√[(sin x - e^(x/2)/25)/x], if sin x - xy^2 > 0 and y(0) = 5
y = -√[(e^(2/3 ln 5 - x/3) - sin x)/x], if sin x - xy^2 < 0 and y(0) = 5
Note that there is no solution for y when sin x - xy^2 = 0.
Visit here to learn more about differential equation : https://brainly.com/question/14620493
#SPJ11
A line segment has endpoints P(2, 3) and Q(4, 6). It is dilated by a scale factor of 3 with a center of dilation at (0, 6). Which statement is true?
Answers
The correct statement is The image segment is longer than the original segment.
To determine the image of the line segment after dilation, we can use the formula for dilation in the coordinate plane. The formula states that the coordinates of the image point (x', y') are related to the coordinates of the original point (x, y) by the following equation:
(x', y') = (h + k(x - h), v + k(y - v))
Where:
(h, v) represents the center of dilation.
k represents the scale factor.
In this case, the center of dilation is (0, 6), and the scale factor is 3. The endpoints of the line segment are P(2, 3) and Q(4, 6). Let's find the image points P' and Q' after dilation.
For point P(2, 3):
x' = 0 + 3(2 - 0) = 0 + 3(2) = 6
y' = 6 + 3(3 - 6) = 6 + 3(-3) = 6 - 9 = -3
Therefore, the image point P' after dilation is P'(6, -3).
For point Q(4, 6):
x' = 0 + 3(4 - 0) = 0 + 3(4) = 0 + 12 = 12
y' = 6 + 3(6 - 6) = 6 + 3(0) = 6 + 0 = 6
Therefore, the image point Q' after dilation is Q'(12, 6).
Now, let's analyze the coordinates of the image points P' and Q' to determine which statement is true.
The image segment is longer than the original segment.
The image segment is shorter than the original segment.
The image segment has the same length as the original segment.
To compare the lengths of the line segments, we can use the distance formula:
Distance = √((x₂ - x₁)² + (y₂ - y₁)²)
For the original segment PQ:
Distance(PQ) = √((4 - 2)² + (6 - 3)²) = √(2² + 3²) = √(4 + 9) = √13
For the image segment P'Q':
Distance(P'Q') = √((12 - 6)² + (6 - (-3))²) = √(6² + 9²) = √(36 + 81) = √117
Since √13 is approximately 3.6056 and √117 is approximately 10.8167, we can conclude that the image segment P'Q' is longer than the original segment PQ.
Therefore, the correct statement is:
The image segment is longer than the original segment.
for such more question on segment
https://brainly.com/question/10496716
#SPJ8
Water leaking onto a floor forms a circular pool. The radius of the pool increases at a rate of 4 cm/min. How fast is the area of the pool increasing when the radius is 9 cm
Answers
When the radius is 9 cm, the area of the circular pool is increasing at a rate of 288π cm square/min.
To find how fast the area of the circular pool is increasing when the radius is 9 cm, we can use the formula for the area of a circle, which is A = πr^2, where A represents the area and r represents the radius.
Given that the radius is increasing at a rate of 4 cm/min, we can differentiate the formula for the area with respect to time (t) using the chain rule:
dA/dt = dA/dr * dr/dt
Here, dA/dt represents the rate of change of the area with respect to time, dr/dt represents the rate of change of the radius with respect to time, and dA/dr represents the derivative of the area with respect to the radius.
To find dA/dr, we can differentiate the formula for the area of a circle:
dA/dr = d/dt (πr^2)
= 2πr * dr/dt
Plugging in the given values, we have:
dr/dt = 4 cm/min
r = 9 cm
Substituting these values into the equation for dA/dr:
dA/dr = 2π(9) * 4
= 72π cm^2/min
Now, we can find dA/dt by multiplying dA/dr by dr/dt:
dA/dt = (72π cm^2/min) * (4 cm/min)
= 288π cm^2/min
To know more about chain rule refer here:
https://brainly.com/question/29498741#
#SPJ11
Find the limit, if it exists, or show that the limit does not exist. lim(,)→(0,0) 2 2 4
Answers
The limit does not exist.
What is a limit?A limit in mathematics is the value that a function approaches when its input approaches some value. Limits are used to define continuity, derivatives, and integrals in calculus and mathematical analysis.In order for such a limit to occur, the fraction \(\frac{x^{2} }{x^{2} +y^{2} }\) must be comparable to the same value \(L\), regardless of the way we take to get there \((0,0)\).
Try approaching \((0,0)\) along the x-axis.
This means setting \(y=0\) and finding the limit \(lim_{x-0} \frac{x^{2} }{x^{2} +y^{2} }\).
We obtain:
\(lim_{x-0,y=0}\frac{x^{2} }{x^{2} +y^{2} } =lim_{y=0}}\frac{x^{2} }{x^{2} +0 }\\=lim_{x-0}} \frac{x^{2} }{x^{2} } \\\\=lim_{x-0}}1\\=1\)
Now evaluate approaching \((0,0)\) along the y-axis.
This means setting \(x=0\) and finding the limit \(lim_{y-0} \frac{x^{2} }{x^{2} +y^{2} }\).
\(lim_{y-0,x-0} \frac{x^{2} }{x^{2} +y^{2} } =lim_{y-0} \frac{0}{0+y^{2} } \\=lim_{y-0} \frac{0}{y^{2} } \\=lim_{y-0} 0\\=0\)
Approaching the origin via these two methods results in distinct limits.
\(lim_{x-0,y-0} \frac{x^{2} }{x^{2} +y^{2} }\) ≠ \(lim_{y-0,x-0}\frac{x^{2} }{x^{2} +y^{2} }\)
Therefore the limit does not exist.
Know more about limits here:
https://brainly.com/question/1521191
#SPJ4
The correct question is given below:
Find the limit, if it exists, or show that the limit does not exist.
\(lim_{(x,y) -(0,0)} \frac{x^{2} }{x^{2} +y^{2} }\)
What is the value of a?

Answers
Answer:
2nd option is the correct answer.
\( 5\frac{1}{3}\: units\)
Step-by-step explanation:
\( In\:\triangle XWZ, \: \angle XWZ= 90°
\\ \: \&\: WY \perp XZ\\\)
Therefore, by geometric mean postulate:
\( WY^2 = XY\times YZ\\
\therefore 4^2 = 3\times a\\
\therefore 16 = 3a
\therefore a = \frac{16}{3}\\\\
\huge \red {\boxed {\therefore a = 5\frac{1}{3}\: units}} \)
Please help!! I am so confused on how to do this.

Answers
Answer:
its 62!
p-by-step explanation:
Answer:
62.
Step-by-step explanation:
A=2(wl+hl+hw)=2·(3·5+2·5+2·3)=62
Which model below represents a fraction that is equivalent to
4
8
Answers
Answer:
4/8 is one half
Step-by-step explanation:
Suppose the lengths of the pregnancies of a certain animal are approximately normally distributed with mean = 246 days and standard deviation 13 days. Complete parts (a) through (1) below
(a) What is the probability that a randomly selected pregnancy lasts less than 242 days?
The probability that a randomly selected pregnancy lasts less than 242 days is approximately (Round to four decimal places as needed)
a
Answers
ANSWER
0.3783
EXPLANATION
The lengths of the pregnancies, X, is normally distributed with a mean of 246 days and a standard deviation of 13 days,
\(X=N(246,13)\)We have to find the probability that a randomly selected pregnancy lasts less than 242 days,
\(P(X<242)=?\)For this, we have to standardize the variable X with the formula,
\(Z=\frac{X-\mu}{\sigma}\)So the probability we have to solve is,
\(P(X<242)=P\mleft(\frac{X-\mu}{\sigma}<\frac{242-\mu}{\sigma}\mright)=P\mleft(Z<\frac{242-246}{13}\mright)=P(Z<-0.31)\)This is equivalent to,
\(P(Z<-0.31)=P(Z>0.31)\)Which is also equivalent to,
\(P(Z>0.31)=1-P(Z<0.31)\)We have to find these equivalences because, usually, normal distribution tables show the probabilities for positive z-scores and to the left of those values - i.e. less than those values. Find z = 0.31 in a z-table,
So, the probability is,
\(P(X<242)=1-P(Z<0.31)=1-0.6217=0.3783\)Hence, the probability that a randomly selected pregnancy lasts less than 242 days is 0.3783.

Decreasing Size of Cattle Herd. Drought has been the major reason for the decrease in the U. S. Cattle herd in recent years. The number of cattle is at its lowest level since 1952. In 2006, there were 96. 6 million head of cattle. This number had fallen to 87. 7 million by 2014. (Source: U. S. Department of Agriculture) Find the average rate of change in the number of cattle from 2006 to 2014
Answers
the average rate of change in the number of cattle from 2006 to 2014 is approximately -1.1125 million head of cattle per year.
To find the average rate of change in the number of cattle from 2006 to 2014, we need to divide the total change in the number of cattle over that period by the number of years.
The total change in the number of cattle is:
87.7 million - 96.6 million = -8.9 million
The number of years is:
2014 - 2006 = 8
So, the average rate of change is:
-8.9 million / 8 years = -1.1125 million per year
learn more about average rate of change here:
https://brainly.com/question/10961052
#SPJ4
The mean time required to repair breakdowns of a certain copying machine is 93 minutes. The company which manufactures the machines claims that breakdowns of its newer model are easier to fix. To test this claim, a sample of 18 breakdowns of the new model were observed, resulting in a mean repair time of 86.8 minutes with a standard deviation of 14.6 minutes. Using a significance level of a = 0.10, determine if the new copy machines are faster to repair. State clearly what your null and alternative hypotheses are, show your work, and state your conclusion.
Answers
A significance level of 0.10, we have enough evidence to conclude that the new copy machines have a significantly faster mean repair time compared to the older model.
To test if the new copy machines are faster to repair, we can set up the following null and alternative hypotheses:
Null Hypothesis (H₀): The mean repair time for the new copy machines is the same as the mean repair time for the older model.
Alternative Hypothesis (H₁): The mean repair time for the new copy machines is less than the mean repair time for the older model.
Let's perform a one-sample t-test to test these hypotheses. The test statistic is calculated as:
t = (sample mean - population mean) / (sample standard deviation / √(sample size))
Given:
Population mean (μ) = 93 minutes
Sample mean (\(\bar x\)) = 86.8 minutes
Sample standard deviation (s) = 14.6 minutes
Sample size (n) = 18
Significance level (α) = 0.10
Calculating the test statistic:
t = (86.8 - 93) / (14.6 / sqrt(18))
t = -6.2 / (14.6 / 4.24264)
t ≈ -2.677
The degrees of freedom for this test is n - 1 = 18 - 1 = 17.
Now, we need to determine the critical value for the t-distribution with 17 degrees of freedom and a one-tailed test at a significance level of 0.10. Consulting a t-table or using statistical software, the critical value is approximately -1.333.
Since the test statistic (t = -2.677) is less than the critical value (-1.333), we reject the null hypothesis.
To know more about significance level:
https://brainly.com/question/4599596
#SPJ4
Pls help me with this work

Answers
Answer:
Step-by-step explanation:
To the 4th power means that all the items in the parenthesis is mulitplied 4 times
(9m)⁴
=9*9*9*9*m*m*m*m*m or
= (9m)(9m)(9m)(9m)
2.) Write the standard number 0.00007396
in scientific notation.
A 7.396 x 10-3
B 7.396 x 10-7
C 7.396 x 10-4
D7.396 x 10-5
Answers
Answer:
7.396 × 10-5
Step-by-step explanation:
To convert 0.00007396 into scientific notation, follow these steps:
Move the decimal 5 times to right in the number so that the resulting number, m = 7.396, is greater than or equal to 1 but less than 10
Since we moved the decimal to the right the exponent n is negative
n = -5
Write in the scientific notation form, m × 10n
= 7.396 × 10-5
Answer:D
0.00007395999999999999 7.396x10-5 7.396e-5 7.396 x 10-5
For box plot data where Q1 = 200, Q2 = 250, and Q3 = 290, the
IQR
Answers
The value of IQR is 90 when box plot data where Q₁ = 200, Q₂ = 250, and Q₃ = 290.
Given that,
For box plot data where Q₁ = 200, Q₂ = 250, and Q₃ = 290
We have to find the data of IQR.
We know that,
IQR is define as the variation in the distribution of your data's middle quartile is measured by the interquartile range (IQR). It is the range that corresponds to your sample's middle 50%. Measure the variability where the majority of your numbers are by using the IQR.
IQR Formula is Q₃ - Q₁
So,
Q₃ = 290
Q₁ = 200
Then ,
IQR = Q₃ - Q₁
IQR = 290 - 200
IQR = 90
Therefore, The value of IQR is 90.
To know more about IQR visit:
https://brainly.com/question/31207390
#SPJ4
Which equation is equivalent to 231 = 10?

Answers
Answer:
4.) log2(10)=3x
Step-by-step explanation:
I think it's correct
im basically just gonna keep putting up sum1 hmu till sum1 with an interesting conversation talks 2 me l-m-a-oooooo
Answers
Answer:
My discord server is very close to 100 membersthe code is: qSnYEsPplease join it :)Or you can copy my name and paste it into the discord join server thingboth worksStep-by-step explanation:
A student is asked to find the vertex of a parabola whose equation is as follows: y = 3 * (x + 4) ^ 2 - 2 The student concludes the vertex is at (4, - 2) . the student correct? If not, what do you think the student did wrong? Explain with as much relevant mathematical detail as possible. Please use at least 3 sentences total in your answer
Answers
Step-by-step explanation:
the general equation of a parabola is
y = a(x – h)² + k.
(h, k) is the vertex of the parabola.
comparing it to
y = 3(x + 4)² - 2
we see that (h, k) = (-4, -2).
the student made a sign mistake. it is "- h" in the squared factor. so, "+4" indicates "-4" as "h".
but the student simply used "+4".
HELPP ‼️‼️‼️ THIS IS DUE LIKE IN A MIN

Answers
Answer:
1, -2
Step-by-step explanation:
The x axis is 1 to the right, and the y axis is 2 down.
You tried 8 of the frozen yogurt flavors shown. In which two ways can you write the fraction of flavors that you tried?
Answers
The solution is, 128 combinations.
What is combination?In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter.
here, we have,
We are told in the question that a frozen yogurt shop has:
8 flavors of frozen yogurt
2 kinds of syrup
8 toppings.
The combinations that can be made with one flavor of frozen yogurt, one syrup, and one topping is calculated as:
8 × 2 × 8
= 128 combinations
Therefore, the combinations that can be made with one flavor of frozen yogurt, one syrup, and one topping is 128 combinations.
To learn more on combination click:
brainly.com/question/10699405
#SPJ1
A. 7.6
B.9
C.7.1
D.8 units
HELPP PLEASEE

Answers
Answer:it will be c
Step-by-step explanation:
9514 1404 393
Answer:
C. 7.1
Step-by-step explanation:
The distance is found using the distance formula:
d = √((x2 -x1)² +(y2 -y1)²)
d = √((1-(-6))² +(1-2)²) = √(7² +(-1)²) = √50
d ≈ 7.07107 ≈ 7.1 . . . . . matches choice C
Find the angle?
Need help please

Answers
Answer:
ans - 25.77°
Step-by-step explanation:
tan a = 14/29
a = tan ^ -1 14/29
a = 25.77°
Answer:
25.77
Step-by-step explanation:
It's logically impossible for this angle to be .008.
Alternatively (the harder way), use trigonometric ratios to solve this problem.
Since you know the adjacent and opposite angle, you need to use tangent ratio.
tan = a/o
Use \(tan^-1\)
\(tan^-1(14/29)\)
a = 25.76932762, ~25.77
Plss help if you can
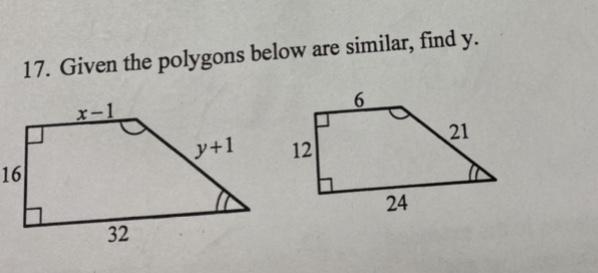
Answers
Answer:
26.93
Step-by-step explanation:
The right polygon is the first one scaled down by 1.33 so we can multiply the values on the 2nd one by 1.33 to get the first one.
y+1 = 21*1.33
y+1 =27.93
y=26.93