Discuss the coordinates of a point P(x, y) on a coordinate plane, and how these can be
described by its distance, r, from the origin and the angle made with the positive x-axis.
Answers
The distance between any coordinate (x,y) and the origin is given by the equation presented as follows:
D = square root of (x² + y²).
The angle between these coordinates and the positive x-axis is given as follows:
Angle = arctan(y/x).
How to obtain the distance and the angle?The distance between two points on a coordinate line is equivalent to the hypotenuse of a right triangle.
The sides of the triangle are represented by the differences of the x-coordinates and the y-coordinates of each point.
For the origin, the coordinates are (0,0), hence the distance of any point from the origin is given by the equation presented as follows:
D = square root of (x² + y²).
For the angle, we have that:
The opposite side to the angle is the difference between the y-coordinates.The adjacent side to the angle is the difference between the x-coordinates.Hence the tangent is applied, as follows:
tan(Angle) = y/x
Angle = arctan(y/x).
More can be learned about the distance between two points at https://brainly.com/question/7243416
#SPJ1
Related Questions
You deposit $2,000 in an account earning 3% interest compounded monthly.
a. How much will you have in the account in 20 years?
b. How much interest will you earn?
Answers
\(~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+\frac{r}{n}\right)^{nt} \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill &\$2000\\ r=rate\to 3\%\to \frac{3}{100}\dotfill &0.03\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{monthly, thus twelve} \end{array}\dotfill &12\\ t=years\dotfill &20 \end{cases}\)
\(A = 2000\left(1+\frac{0.03}{12}\right)^{12\cdot 20}\implies A=2000(1.0025)^{240} \implies \boxed{A \approx 3641.51} \\\\\\ 3641.51~~ - ~~2000~~ \approx~~ \stackrel{earned~interest}{\boxed{1641.51}}\)
Victor biked from his hometown to a neighboring city in 6 hours. He biked back to his hometown in 4 hours. His speed on the return trip was 4 mph faster than his speed on the first trip. How far apart are the two cities?
Answers
We will have the following:
His speed on the return (r) trio was 4mph faster than his speed in the first trip (o), so:
\(r=o+4\)Then, we have that speed times distance equals time, and distance is equal to time over speed. Thus:
\(6h(\frac{x}{\text{hours}})=4h(\frac{x+4}{\text{hours}})\)Then, we have:
\(6x=4x+16\Rightarrow2x=16\)\(\Rightarrow x=8\)So, the initial speed was of 8mph.
Then we deternine the distance:
\(d=(8mi/h)(6h)\Rightarrow d=48mi\)So, the two cities are 48 miles apart.
Two lines in the plane of a floor are
Answers
Answer:
never skew
Step-by-step explanation:
What is the value of the expression when a = 2 and b = 3 ? 4a + b - 2 Question 1 options: 7 9 12
Answers
Answer:
9
Step-by-step explanation:
4 * 2 + 3 - 2 =
= 8 + 1 =
= 9
The circle with center O shown above has a 34° inscribed angle and a 42° central angle. What is the measure of minor arc ABC?
Answers
The measures of the three intercepted arcs from least to greatest are;
AC < BC < AB
We have,
We are given that
Angle ACB = 63 degrees
Arc BC is 118 degrees.
Now, from the Triangle angle sum theorem, we know that the sum of all interior angles of any triangle is always equal to 180 degrees.
Thus, the sum of the interior angles of the inscribed triangle given to us id also 180 degrees.
Now, since Angle ACB = 63 degrees
Then Arc AB = 63 * 2 = 126
Arc AC = 360 - (Arc BC + Arc AB)
We are given BC = 118 degrees
Thus;
Arc AC = 360 - (118 + 126)
Arc AC = 116°
Thus, the least arc angle is Arc AC while the greatest is Arc AB
Read more about missing side of triangle at; brainly.com/question/24279384
#SPJ1
complete question:
Triangle ABC is inscribed in a circle centered at point O.
The figure shows triangle ABC is inscribed in a circle centered at point O and has an angle ACB is 63 degrees and arc BC is 118 degrees.
Order the measures of the three intercepted arcs from least to greatest.
if m<xyz = 58 and m<wxz = 51 find m<wzx
Answers
Answer:
m<wzx = 71
Step-by-step explanation:
Assuming these are interior angles of a triangle.
The sum of all three interior angles of a triangle is always 180 degrees, therefore:
m<xyz + m<wxz + m<wzx = 180
Substitute our values:
58 + 51 + m<wzx = 180
m<wzx = 180 - 58 - 51
m<wzx = 71
A group consists of five men and five women. Three people are selected to attend a conference.
A. In how many ways can three people be selected from this group of ten?
B. In how many ways can three women be selected from the five women?
C. Find the probability that the selected group will consist of all women.
Answers
Answer:
a) 120
b) 10
c) 1/12
Step-by-step explanation:
The number of ways that a sample of r can be selected from a population of n is:
nCr = n! / (r! (n−r)!)
a) 3 people selected from a group of 10
₁₀C₃ = 120
b) 3 women selected from a group of 5
₅C₃ = 10
c) Of the 120 committees that can be chose, 10 are all women. So the probability is 10/120 = 1/12.
Nick needs 75 yards of wire for a project. If the wire is only sold on spools which hold 6 feet of wire, how many spools will he need? Nick needs spools .
Answers
Answer:
12.5
Step-by-step explanation:
Answer:
37.5
Step-by-step explanation:
I have 0 idea what this even means? Does anyone know the answer and if you could possibly elaborate if you do? Very confused over here
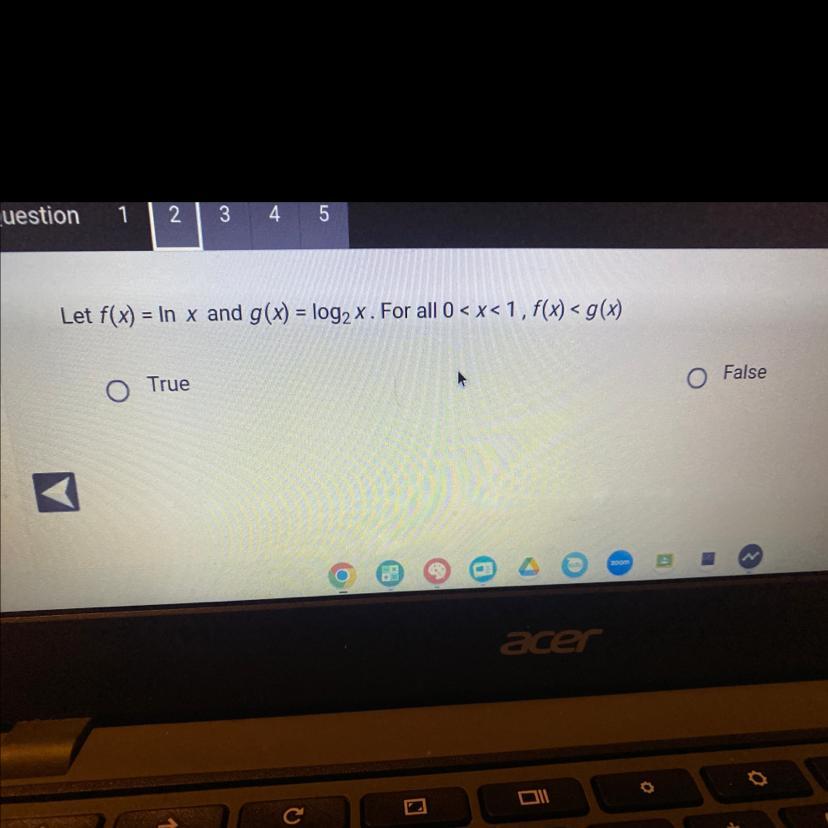
Answers
Let f(x) = lnx and g(x) = log₂x. for all 0 < x < 1, f(x) < g(x): True.
How to determine the corresponding output value for this function?In this scenario and exercise, we would determine the corresponding output value for the functions f(x) and g(x) under the given mathematical operation and independent variables.
When x = 1, the output value for f(x) based on the table of values is given by;
f(x) = lnx
f(1) = ln(1).
f(1) = 0.
When x = 2, the output value for f(x) based on the table of values is given by;
f(x) = lnx
f(2) = ln(2).
f(2) = 0.69314718
When x = 1, the output value for g(x) based on the table of values is given by;
g(x) = log₂x
g(1) = log₂(1)
g(1) = 0.
When x = 2, the output value for g(x) based on the table of values is given by;
g(x) = log₂x
g(2) = log₂(2)
g(2) = 1.
In this context, we can logically deduce that the function f(x) is less than function g(x) for all 0 < x < 1.
Read more on function here: brainly.com/question/10687170
#SPJ1
Solve x≤0 or x≥−4 and write the solution in interval notation.
Answers
Answer:
-4 ≤ x ≤ 0
Step-by-step explanation:
Given
x ≤ 0 or x ≥ -4
Required
Write using Interval notation
x ≤ 0 or x ≥ -4
This can be rewritten as
x ≤ 0 or -4 ≤ x
Reorder the above inequality to give:
-4 ≤ x or x ≤ 0
The above inequality can then be combined to give
-4 ≤ x ≤ 0
Hence, the interval notation of x ≤ 0 or x ≥ -4 is -4 ≤ x ≤ 0
If I make $84000 a year, how much is that per month?
Answers
Answer:
$|-7000|
Step-by-step explanation:
divide 84000 by 12 = 7000
Answer:
7,000.00
Step-by-step explanation:
if you have 84,000 and divide it by 12 you would get 7,000.
In the 2006 season, Tom Brady threw for 3,529
yards. In the 2007 season, he threw for 2,806
yards. What is the percentage decrease
Answers
3529-2806=723
(723/35290)x100= 20.4873901955
First, work out the difference (decrease) between the two numbers you are comparing. Next, divide the decrease by the original number and multiply the answer by 100. If the answer is a negative number, this is a percentage increase.
Answer:
59.02%
Step-by-step explanation:
SO SORRY THAT THIS IS LATE anyway what you is minus the biggest number by the smallest number which would be 3,529 - 2,806 = 723
BECAUSE 3,529 is the original number you would do 723 / 3,529 = 0.5902521
then you would times that number by 100
0.5902521 x 100 = 59.02%
hope this helps
3. There are shows scheduled for Theater A next week. All of the tickets for the seats have been sold. What is the expected attendance for next week?
Answers
Answer:
Initially, national security was defined as the government's ability to protect its citizens from military attacks. Today, this definition also includes other non-military areas such as defense against crime and terrorism, economic security, environmental security, food security, energy security and cyber security.
If A = (0,0) and B = (8, 2), what is the length of AB?
A. 8.25 units
B. 9.41 units
C. 3.16 units
D. 7.75 units
Answers
Answer:
8.25
= root under (8-0)^2+(2-0)^2
= root under (8)^2+(2)^2
=root under 64+4
= root under 68
8.25 units
I hope this will help you and plz mark me as brainest answer
How far above ground is the top of the pole?

Answers
Answer:
I would say about 7 feet and 1 inch
Step-by-step explanation:
(6.2 x 10²) x (3.5 x 10³)
Answers
Answer:
\(21.7 x 10^5\)
Step-by-step explanation:
(6.2 x 10²) x (3.5 x 10³)
First, multiply the coefficients: 6.2 x 3.5 = 21.7.
Then, add the exponents: 10² x 10³ = 10^(2+3) = 10^5.
Therefore, the result is 21.7 x 10^5.
Answer:
3286000
Step-by-step explanation:

How would you write the equation with a slope of 2/3 and a y-intercept of -3 in slope- intercept form
Answers
y=2/3x-2
Explanation:
The equation of a line can be written as y=mx+c
m=slope and c = y-intercept
The point at the x−intercept has coordinates (-3,0)
In y=mx+c
0=2/3(3)+c
0=2+c
-2=c
The equation is y=2/3x-2
Answer:
\( y = \frac{2}{3} x - 3\)
Step-by-step explanation:
Slope (m) = 2/3
y-intercept (b) = - 3
Equation of line in slope intercept form is given as:
\( y = mx + b\)
Plug the values of m and b in the above equation, we find:
\(y = \frac{2}{3} x + ( - 3) \\ \\ y = \frac{2}{3} x - 3\)
Chris and Mary are selling tickets at their class play. Chris is selling student tickets for $4.00 each, and Mary selling adult tickets for $6.50 each. If their total income for 21 tickets was $124.00, how many tickets did Chris and Mary sell individually?
Answers
Answer:
Chris sells 5 tickets and Mary sells 16 tickets
Step-by-step explanation:
System of Equations
To solve the problem we call:
x = number of tickets sold by Chris
y = number of tickets sold by Mary
They sold a total of 21 tickets, thus:
x + y = 21 [1]
Mary sold adult tickets for $6.50 each and Chris sold student tickets for $4.00 each. The total income was:
4x + 6.5y = 124 [2]
Multiplying [1] by -4:
-4x - 4y = -84 [3]
Adding [2] and [3]:
2.5y = 40
Dividing by 2.5:
y = 40/2.5
y = 16
From [1]
x = 21 - 16 = 5
x = 5
Chris sells 5 tickets and Mary sells 16 tickets
Please solve this
∫ (log(1 + x ^ 2))/((x + 1) ^ 2) dx
Answers
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
We have,
To solve the integral ∫ (log(1 + x²) / (x + 1)²) dx, we can use the method of substitution.
Let's substitute u = x + 1, which implies du = dx. Making this substitution, the integral becomes:
∫ (log(1 + (u-1)²) / u²) du.
Expanding the numerator, we have:
∫ (log(1 + u² - 2u + 1) / u²) du
= ∫ (log(u² - 2u + 2) / u²) du.
Now, let's split the logarithm using the properties of logarithms:
∫ (log(u² - 2u + 2) - log(u²)) / u² du
= ∫ (log(u² - 2u + 2) / u²) du - ∫ (log(u²) / u²) du.
We can simplify the second integral:
∫ (log(u²) / u²) du = ∫ (2 log(u) / u²) du.
Using the power rule for integration, we can integrate both terms:
∫ (log(u² - 2u + 2) / u²) du = log(u² - 2u + 2) / u - 2 ∫ (log(u) / u³) du.
Now, let's focus on the second integral:
∫ (log(u) / u³) du.
This integral does not have a simple closed-form solution in terms of elementary functions.
It can be expressed in terms of a special function called the logarithmic integral, denoted as Li(x).
Therefore,
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
Learn more about integrations here:
https://brainly.com/question/30217024
#SPJ1
8. A pyramid has a volume of 8 cubic feet. The height is 2 feet. The base is rectangular. Give possible dimensions for the length and width of the base.
Answers
Answer:
base = 12 ft²
The base could be 3 ft x 4 ft, 6 ft x 2 ft, etc. (any numbers multiplied together = 12)
Step-by-step explanation:
volume = 1/3bh
8 = 1/3b(2)
multiply both sides of the equation by 3:
24 = 2b
b = 12 ft²
Write an expression to represent:
5 times the sum of x and 3
Answers
Answer:
5(x + 3)
Step-by-step explanation:
the sum of x and 3 is x + 3, then multiply by 5 to obtain
5(x + 3)
(y + 2)² when y=-7, z = 19
Answers
Answer:
Step-by-step explanation:
if y=-7 you can plug it in the equation\(=(-7+2)^{2} \\=(-5)^{2} \\=25\)Which correlation coefficient could represent the relationship in the scatterplot?
Answers
The correlation coefficient that could represent the relationship in the scatterplot is B. -.098.
What is a correlation coefficient?A correlation coefficient is a number between -1 and 1 that is meant to show the strength of the relationship between two variables.
When the relationship between the variables is negative - one variable increases while the other variable decreases - then the correlation coefficient will be negative.
As we can see in the graph, the relationship between time spent practicing and number of notes played incorrectly is negative. The correlation coefficient will therefore be negative.
-0.098 is therefore the best answer because it is negative. -1.43 is beyond the range of -1 to 1 so cannot be a correlation coefficient.
Options for this question:
A) 0.34 B) -.098 C) -1.43 D) 0.99
Find out more on correlation coefficients at https://brainly.com/question/4219149
#SPJ1

A message is coded into the binary symbols 0 and 1 and the message is sent over a communication channel.
The probability a 0 is sent is 0.4 and the probability a 1 is sent is 0.6. The channel, however, has a random error that
changes a 1 to a 0 with probability 0.1 and changes a 0 to a 1 with probability 0.2. Show your work below.
a. What is the probability a 1 is received?
b. If a 1 is received, what is the probability a 0 was sent?
Answers
Answer:
A: the probability that a 1 is received is 0.56.
B: the probability that a 0 was sent given that a 1 is received is (2/25) * (1 - P(0 sent)).
Step-by-step explanation:
To solve this problem, we can use conditional probabilities and the concept of Bayes' theorem.
a. To find the probability that a 1 is received, we need to consider the two possibilities: either a 1 was sent and remained unchanged, or a 0 was sent and got flipped to a 1 by the random error.
Let's denote:
P(1 sent) = 0.6 (probability a 1 is sent)
P(0→1) = 0.2 (probability a 0 is flipped to 1)
P(1 received) = ?
P(1 received) = P(1 sent and unchanged) + P(0 sent and flipped to 1)
= P(1 sent) * (1 - P(0→1)) + P(0 sent) * P(0→1)
= 0.6 * (1 - 0.2) + 0.4 * 0.2
= 0.6 * 0.8 + 0.4 * 0.2
= 0.48 + 0.08
= 0.56
Therefore, the probability that a 1 is received is 0.56.
b. If a 1 is received, we want to find the probability that a 0 was sent. We can use Bayes' theorem to calculate this.
Let's denote:
P(0 sent) = ?
P(1 received) = 0.56
We know that P(0 sent) + P(1 sent) = 1 (since either a 0 or a 1 is sent).
Using Bayes' theorem:
P(0 sent | 1 received) = (P(1 received | 0 sent) * P(0 sent)) / P(1 received)
P(1 received | 0 sent) = P(0 sent and flipped to 1) = 0.4 * 0.2 = 0.08
P(0 sent | 1 received) = (0.08 * P(0 sent)) / 0.56
Since P(0 sent) + P(1 sent) = 1, we can substitute 1 - P(0 sent) for P(1 sent):
P(0 sent | 1 received) = (0.08 * (1 - P(0 sent))) / 0.56
Simplifying:
P(0 sent | 1 received) = 0.08 * (1 - P(0 sent)) / 0.56
= 0.08 * (1 - P(0 sent)) * (1 / 0.56)
= 0.08 * (1 - P(0 sent)) * (25/14)
= (2/25) * (1 - P(0 sent))
Therefore, the probability that a 0 was sent given that a 1 is received is (2/25) * (1 - P(0 sent)).
A message is coded into the binary symbols 0 and 1 and the message is sent over a communication channel. The probability a 0 is sent is 0.4 and the probability a 1 is sent is 0.6. The channel, however, has a random error that changes a 1 to a 0 with probability 0.2 and changes a 0 to a 1 with probability 0.1. (a) What is the probability a 0 is received? (b) If a 1 is received, what is the probability a 0 was sent?
find the mean and median of each of the following sets of data. determine the deviation from the mean for each data point within the sets and find the mean deviation for each set. 24.49 24.68 24.77 24.83 24.73
Answers
The average distance from the mean is 0.09.
The mean is also known as the average and is calculated by adding up all the values in the set and then dividing the sum by the total number of values.
So, for the given set of data: 24.49, 24.68, 24.77, 24.83, 24.73, the mean would be calculated as follows:
Mean = (24.49 + 24.68 + 24.77 + 24.83 + 24.73) / 5
= 24.70
It tells us what the typical value is within the data set. In this case, the mean value of the data set is 24.70.
Next, let's find the median of the set of data. The median is the middle value of a data set when it is arranged in numerical order. In this case, the data set is already arranged in numerical order, so we can easily find the median.
The median value of the data set is the middle value, which is 24.77.
Now, we will calculate the deviation from the mean for each data point within the set. The deviation from the mean tells us how far each value is from the mean value. This is calculated by subtracting the mean from each value in the set.
Deviation from the mean for each data point:
-0.21, -0.02, 0.07, 0.13, 0.03
As you can see, some values are above the mean, and some are below the mean. The deviation from the mean can be used to determine how spread out the data is from the mean value.
Finally, we will calculate the mean deviation for the set. The mean deviation is the average of the absolute values of the deviation from the mean.
Mean deviation = (|(-0.21)| + |(-0.02)| + |0.07| + |0.13| + |0.03|) / 5
= 0.09
The mean deviation tells us the average distance from the mean value.
To know more about mean here.
https://brainly.com/question/22871228
#SPJ4
The following table presents the time taken to review articles that were submitted for publication to a particular journal during a recent year. A few articles took longer than 6 months to review; these are omitted from the table. Consider the data to be a population. (image) (a) Approximate the variance of the times. Round the answer to at least two decimal places. The variance is (b) Approximate the standard deviation of the times. Round the answer to at least two decimal places. The standard deviation is

Answers
Answer:
Variance = 0.1645
Standard deviation = 0.4056
Step-by-step explanation:
Kindly check attached picture for detailed explanation

a) 9-12/2
b) 27-13/²2

Answers
a) Option a) 9 - 1/2 is equal to 17/2.
b) Option b) 27 - 2/3 is equal to 79/3.
a) The expression 9 - 1/2 can be simplified by finding a common denominator for the terms. The common denominator for 9 and 1/2 is 2.
Multiplying 9 by 2/2, we get:
9 * (2/2) = 18/2
So, the expression 9 - 1/2 can be simplified to:
18/2 - 1/2 = 17/2
Therefore, option a) 9 - 1/2 is equal to 17/2.
b) The expression 27 - 2/3 can be simplified in a similar manner by finding a common denominator for the terms. The common denominator for 27 and 2/3 is 3.
Multiplying 27 by 3/3, we get:
27 * (3/3) = 81/3
So, the expression 27 - 2/3 can be simplified to:
81/3 - 2/3 = 79/3
Therefore, option b) 27 - 2/3 is equal to 79/3.
for such more question on simplified
https://brainly.com/question/11680269
#SPJ8
what are the zeroes of f(x)=(x-7)(x+8)
Answers
Answer:
The zeroes of f(x) = (x-7)(x+8) are 7 and -8.
Step-by-step explanation:
You have to figure out what makes each of the equal to zero.
Step 1 : Make the 2 equations both equal 0.
x-7 = 0
x+8 = 0
Step 2: Solve for x
x-7 = 0
x=7
x+8 = 0
x=-8
So 7 and -8 are both zeroes of this function.
Randy's gross salary is $760 per week. his salary is taxed at 16% what is his net salary
Answers
Answer:
$638.4
Step-by-step explanation:
Randy's gross salary (salary without any deduction) = $760
taxed rate =16%
Amount tax paid =tax% of gross income
=16/100 * $760
=$16*760/100
=$12160/100
=$121.6
net salary = gross salary - tax paid
=$760 - $ 121.6
=$638.4
Randy's net salary is $638.40
Randy's gross salary = $760 per week.
Tax paid on his salary = 16%
Net salary is the difference between the salary earned and the amount paid as tax. This will be:
= Salary - Tax
= $760 - (16% × $760)
= $760 - (0.16 × $760)
= $760 - $121.60
= $638.40
Read related link on:
https://brainly.com/question/23421215
If c(x) = 2x^2 - 4x + 3 and d(x) = -x^3 + x + 1 find c(3a)
Answers
Answer:
c(3a) = 2(3a)^2 - 4(3a) + 3 = 18a^2 - 12a + 3.
Step-by-step explanation:
c(3a) = 18a^2 - 12a + 3
Note: this is the simplified form of the expression.