Determining if a function is linear which table represent a linear function?

Answers
Answer: It’s the last one, D
Step-by-step explanation: because It’s the last one, D
The correct function which is linear shown in table 4.
What is mean by Function?A relation between a set of inputs having one output each is called a function. and an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
Given that;
To find a function is linear which table represent a linear function.
Now, From table 4;
Rate of change are,
⇒ (3 - 1) / (1 - 0)
⇒ 2
⇒ (5 - 3) / (2 - 1)
⇒ 2
Thus, The correct function which is linear shown in table 4.
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ7
Related Questions
Find any points of discontinuity for the rational function.
Answers
The points of discontinuity for a rational function occur when the denominator is equal to zero.
In a rational function, the denominator represents the values where the function is undefined. To find the points of discontinuity, we need to identify the values that make the denominator zero. These values are the zeros of the denominator.
When the denominator is zero, the rational function is undefined because division by zero is not possible. Thus, the points of discontinuity are the values that make the denominator zero, but are not canceled out by factors in the numerator. These points can be vertical asymptotes or removable discontinuities, depending on the factors present in the numerator. It is important to check for these points and understand their nature when analyzing rational functions.
Learn more about rational functions here
brainly.com/question/27914791
#SPJ11
What are the points of discontinuity for the given rational function?
What outcome is likely to occur for a hypothesis test evaluating a treatment that has a very large and robust effect?
Answers
For the given statement, we have to correctly rejecting the null hypothesis.
According to the statement
we have to find the outcome when hypothesis test evaluating a treatment that has a very large and robust effect.
For this purpose, we know that the
A hypothesis is a testable statement about the relationship between two or more variables or a proposed explanation for some observed phenomenon.
And according to the given statement it is clear that the by this we have to rejected this hypothesis.
because this treatment and the large effects are not possible for the independent values of the hypothesis.
In other words, we can say that the we have to correctly rejecting the null hypothesis.
So, For the given statement, we have to correctly rejecting the null hypothesis.
Learn more about hypothesis here
https://brainly.com/question/11555274
#SPJ4
The auxiliary equation for the given differential equation has complex roots. Find a general solution. y" - 10y' +29y=0
Answers
The general solution to the given differential equation y" - 10y' + 29y = 0, where the auxiliary equation has complex roots, is given by y(x) = e^(5x)(C1cos(2x) + C2sin(2x)), where C1 and C2 are arbitrary constants.
To find the general solution of the given differential equation, we first solve the auxiliary equation, which is obtained by substituting y(x) = e^(rx) into the homogeneous equation. The auxiliary equation for the given differential equation is r^2 - 10r + 29 = 0.
Solving this quadratic equation, we find that the roots are complex: r = 5 ± 2i. Since the roots are complex, we can express them as r = 5 ± 2i.
Using Euler's formula, e^(ix) = cos(x) + isin(x), we can rewrite e^(2ix) as cos(2x) + i sin(2x). Therefore, the general solution can be written as y(x) = e^(5x)(C1cos(2x) + C2sin(2x)), where C1 and C2 are arbitrary constants.
This general solution represents a linear combination of the exponential function e^(5x) and the trigonometric functions cosine and sine with a double frequency of 2x.
Hence, the general solution to the given differential equation is y(x) = e^(5x)(C1cos(2x) + C2sin(2x)), where C1 and C2 are arbitrary constants.
To learn more about differential equation: -brainly.com/question/32645495
#SPJ11
A FOOTBALL MATCH STARTED AT 10:00AM AND FINISHED AT 2:30PM HOW LONG DID THE GAME LAST
Answers
how do i find the inverse

Answers
Step-by-step explanation:
To solve for inverse, utilize the following steps.
Step 1: let f(x)=y so we get
\(y = \sqrt{x - 6} + 5\)
Step 2: Swap y and x
\(x = \sqrt{y - 6} + 5\)
Solve for y.
\(x - 5 = \sqrt{y - 6} \)
\((x - 5) { }^{2} + 6 = y\)
Step 4: Let y =f^-1(x)
\((x - 5) {}^{2} + 6 = f {}^{ - 1} (x)\)
Answer: \(f^{-1}(x) =\) x²-10x+19
Step-by-step explanation:
Let's replace f(x) for y for now.
\(y=\sqrt{x-6}+5\)
To find inverse. make your y into x, and your x into y
\(x=\sqrt{y-6}+5\) >Now you solve for y. subtract 5 from both sides
\(x-5=\sqrt{y-6}\) >Square both sides to get rid of root
\((x-5)^{2} =(\sqrt{y-6})^{2}\) >drop root and square (x-5)
(x-5)(x-5) = y-6 >FOIL
x²-5x-5x+25 = y-6 > combine like terms
x²-10x+25 = y-6 >add 6 to both sides
x²-10x+19=y > this is your inverse now put the y into inverse form
\(f^{-1}(x) =\) x²-10x+19
What is the slope of the line represented by:
5x-12y = 24
Answers
Answer:
5/12
Step-by-step explanation:
5x - 12y = 24
~Subtract 5x to both sides
-12y = 24 - 5x
~Divide -12 to everything
y = -2 + 5/12x
~Reorder
y = 5/12x - 2
Slope is represent by "m" in slope intercept form [ y = mx + b ]. As we can see m = 5/12 from the given information.
Best of Luck!
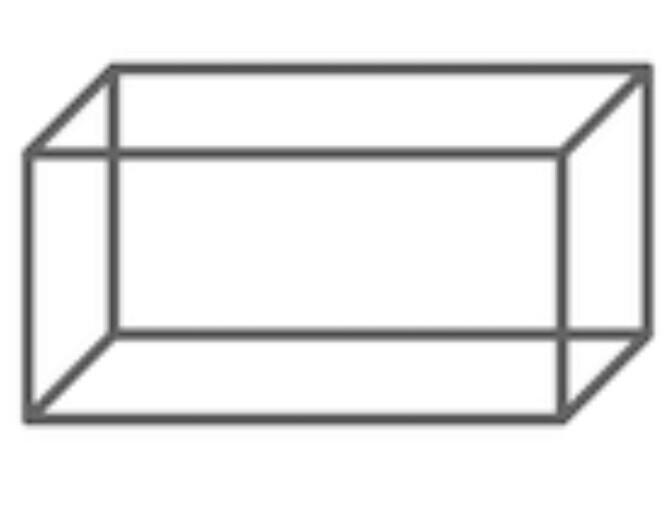
Can someone help me with number 17?

Answers
Answer:
Vertices = 8
Edges = 12
Faces = 6
Step-by-step explanation:
A cuboid ( or a rectangular solid ) has 8 vertices , 12 edges & 6 faces.
In Problems 55-62, write each function in terms of unit step functions. Find the Laplace transform of the given function 0 =t< 1 57. f(t) = {8 12 1 Jo, 0 =t < 30/2 58. f(t) = ( sint, t = 30/2
Answers
The Laplace transform of the given function is,
L{f(t)} = (8/s) - 4e^{-3s/2}/s - 6e^{-2s}/s
Given function is f(t) = {8 12 1 Jo, 0 ≤ t < 3/2, 3/2 ≤ t < 2, 2 ≤ t < ∞ respectively.
We have to find Laplace transform of the given function.
For first interval 0 ≤ t < 3/2,
f(t) = 8u(t) - 8u(t-3/2)
For second interval 3/2 ≤ t < 2,
f(t) = 12u(t-3/2) - 12u(t-2)
For third interval 2 ≤ t < ∞,
f(t) = Jo(u(t-2))
Hence, we can write the Laplace transform of the given function as,
L{f(t)} = L{8u(t) - 8u(t-3/2)} + L{12u(t-3/2) - 12u(t-2)} + L{Jo(u(t-2))}
Where, L is Laplace transform.
Let's calculate each Laplace transform stepwise,
1. L{8u(t) - 8u(t-3/2)}L{8u(t)} = 8/L{u(t)}L{u(t)}
= 1/sL{u(t-3/2)}
= e^{-3s/2}/s
Therefore,
L{8u(t) - 8u(t-3/2)} = 8[1/s - e^{-3s/2}/s]
2. L{12u(t-3/2) - 12u(t-2)}L{12u(t-3/2)}
= 12e^{-3s/2}/sL{12u(t-2)}
= 12e^{-2s}/s
Therefore,
L{12u(t-3/2) - 12u(t-2)} = 12[e^{-3s/2}/s - e^{-2s}/s]
3. L{Jo(u(t-2))}L{Jo(u(t-2))} = ∫_{0}^{∞}δ(t-2)e^{-st}dtL{Jo(u(t-2))}
= e^{-2s}
Hence, the Laplace transform of the given function is,
L{f(t)} = 8[1/s - e^{-3s/2}/s] + 12[e^{-3s/2}/s - e^{-2s}/s] + e^{-2s}
= (8/s) - 4e^{-3s/2}/s - 6e^{-2s}/s
To know more about Laplace visit:
https://brainly.com/question/30759963
#SPJ11
Drag each label to the correct image. Each label can be used more than once, but not all labels will be used. A cube is a rectangular prism whose faces are all squares with sides of the same length. Match each cross section of the cube to its correct image.
Answers
Answer:
From left to right it's square square rectangle.
Help please
Solve for j.
j=

Answers
Answer:
j=15
Step-by-step explanation:
Let's set up an equation:
2j+7=37
Subtract both sides by 7
2j=30
Divide both sides by 2
j=15
Answer:
15
Step-by-step explanation:
37=2j+7
so subract 7 from both sides
30=2j
then divide by 2 on each side
j=15
Find the 6th term of the geometric sequence whose common ratio is 3/2 and whose first term is 4
Answers
6th terms of given geometric progression whose common ratio is 3/2 and first term is 4 is 243/8 using the farmula ar^(n-1).
What is a geometric sequence?
A mathematical sequence known as a geometric progression (GP) is one in which each following phrase is generated by multiplying each preceding term by a fixed integer, or "common ratio." This progression is sometimes referred to as a pattern-following geometric sequence of numbers. Learn development in mathematics here as well. Here, each phrase is multiplied by the common ratio to generate the subsequent term, which is a non-zero value. A geometric series with a common ratio of 2 is 2, 4, 8, 16, 32, 64, etc.
Geometric Progression takes the following general form: a, ar, ar^2, ar^3, ar^4,..., ar^(n-1).
a = First term where
The common Ratio is r.
nth term = ar^(n-1)
6th terms ar^(6-1) = ar^5.
given is that r =3/2. a = 4.
6th term = 4 * (3/2)^5
= 4 * 3^5/2^5
=4*243/4*8
=243/8.
To know more about geometric progression here:
https://brainly.com/question/4853032
#SPJ4
According to a recent report, a sample of 360 one-year-old baby boys in the United States had a mean weight of 25.5 pounds. Assume the population standard deviation is =σ5.1 pounds.Construct a 99.5% confidence interval for the mean weight of all one-year-old baby boys in the United States. Round the answer to at least one decimal place.
Answers
The 99.5% confidence interval for the mean weight of all one-year-old baby boys in the United States is (24.8, 26.2) pounds.
We are given a sample of 360 one-year-old baby boys in the United States with a mean weight of 25.5 pounds and a population standard deviation of σ=5.1 pounds. We need to construct a 99.5% confidence interval for the mean weight of all one-year-old baby boys in the United States.
To construct the confidence interval, we can use the formula:
Confidence interval = sample mean ± (z-score)(standard error)
where the z-score is based on the confidence level and the standard error is calculated as:
standard error = σ/√n
Plugging in the given values, we get:
standard error = 5.1/√360 = 0.27 pounds
Since we want a 99.5% confidence interval, the corresponding z-score is 2.807. Therefore, the confidence interval is:
Confidence interval = 25.5 ± (2.807)(0.27) = (24.8, 26.2) pounds
We can be 99.5% confident that the mean weight of all one-year-old baby boys in the United States falls within the range of 24.8 to 26.2 pounds.
To know more about z-score visit:
https://brainly.com/question/29187588
#SPJ11
Consider the differential equation dy/dx = y^2 (2x + 2). Let y = f (x) be the particular solution to the differential equation with initial condition f(0) = -1.(a) find lim\frac{f(x)+1}{sinx}Show the work that leads to your answer.(b) Use Euler's method, starting at x = 0 with two steps of equal size, to approximate f(1/2).(c) find y = f (x), the particular solution to the differential equation with initial condition f(0) = -1
Answers
The limit of (f(x) + 1) / sin(x) as x approaches 0 is 0, the approximation for f(1/2) using Euler's method with two steps is 19/32 and the particular solution to the differential equation with the initial condition f(0) = -1 is: y(x) = -1 / (x² + 2x + 1) - 1.
(a) To find the limit of (f(x) + 1) / sin(x) as x approaches 0, we can first rewrite the given differential equation as:
dy / dx = y² (2x + 2)
Separating variables, we get:
dy / y² = (2x + 2) dx
Integrating both sides, we have:
∫(1 / y² ) dy = ∫(2x + 2) dx
Integrating the left side gives:
-1 / y = x² + 2x + C1
where C1 is the constant of integration.
Since we have the initial condition f(0) = -1, we substitute x = 0 and y = -1 into the above equation:
-1 / (-1) = 0² + 2(0) + C1
1 = C1
So the particular solution is:
-1 / y = x² + 2x + 1
Multiplying through by y gives:
-1 = y(x² + 2x + 1)
Simplifying further:
y(x² + 2x + 1) + 1 = 0
Now, to find the limit (f(x) + 1) / sin(x) as x approaches 0, we substitute x = 0 into the particular solution equation:
f(0)(0² + 2(0) + 1) + 1 = 0
-1(0) + 1 = 0
1 = 0
Therefore, the limit of (f(x) + 1) / sin(x) as x approaches 0 is 0.
(b) Using Euler's method, we approximate the value of f(1/2) starting at x = 0 with two steps of equal size. Let's choose the step size h = 1/4.
First step:
x0 = 0, y0 = f(0) = -1
Using the differential equation, we have:
dy / dx = y² (2x + 2)
dy = y² (2x + 2) dx
Approximating the derivative using the Euler's method:
Δy ≈ y² (2x + 2) Δx
Δy ≈ (-1)² (2(0) + 2) (1/4)
Δy ≈ 1/2
Next, we update the values:
x1 = x0 + Δx = 0 + 1/4 = 1/4
y1 = y0 + Δy = -1 + 1/2 = 1/2
Second step:
x0 = 1/4, y0 = 1/2
Using the differential equation again:
dy / dx = y^2 (2x + 2)
dy = y² (2x + 2) dx
Approximating the derivative using the Euler's method:
Δy ≈ y² (2x + 2) Δx
Δy ≈ (1/2)² (2(1/4) + 2) (1/4)
Δy ≈ 3/32
Updating the values:
x2 = x1 + Δx = 1/4 + 1/4 = 1/2
y2 = y1 + Δy = 1/2 + 3/32 = 19/32
Therefore, the approximation for f(1/2) using Euler's method with two steps is 19/32.
c)To find the particular solution to the differential equation dy/dx = y^2 (2x + 2) with the initial condition f(0) = -1, we can solve the separable differential equation.
Separating variables, we have:
dy / y² = (2x + 2) dx
Integrating both sides:
∫(1 / y² ) dy = ∫(2x + 2) dx
Integrating the left side:
-1 / y = x² + 2x + C
where C is the constant of integration.
To find the particular solution, we substitute the initial condition f(0) = -1:
-1 / (-1) = 0² + 2(0) + C
1 = C
So the particular solution is:
-1 / y = x² + 2x + 1
Multiplying through by y gives:
-1 = y(x² + 2x + 1)
Simplifying further:
y(x² + 2x + 1) + 1 = 0
Therefore, the particular solution to the differential equation with the initial condition f(0) = -1 is: y(x) = -1 / (x² + 2x + 1) - 1
To know more about differential check the below link:
https://brainly.com/question/28099315
#SPJ4
Does anyone know the answer to this?

Answers
the answer is b. y-5=1/2(x+3)^2
9514 1404 393
Answer:
B. y -5 = (1/2)(x +3)^2
Step-by-step explanation:
The parent function f(x) = x^2 has been shifted left 3 and up 5, and scaled vertically. The translation of the vertex to (h, k) can be modeled by ...
y -k = a(x -h)^2
For (h, k) = (-3, 5), the form of the answer will be ...
y -5 = a(x +3)^2
Only one answer choice has that form.
_____
Additional comment
The coefficient 'a' will be positive when the parabola opens upward. This eliminates choices A and C. Choice D represents a translation of 3 units right and 5 units down—directions opposite of those shown on this graph.

can someone help me out with these .

Answers
Question 7 I need help on thank you

Answers
Find the slope of the line.
*

Answers
Help me plases. thank you

Answers
The length of leaves from a tree. The correct option D.
Describe Measurement Units?Measurement units are standardized systems used to quantify and express the magnitude or size of physical quantities. They provide a common language for scientists, engineers, and other professionals to communicate about the physical world.
Measurement units are typically classified into two main categories: base units and derived units. Base units are the fundamental building blocks of measurement and are used to define other units. Derived units are created by combining base units and are used to measure quantities that are derived from the fundamental ones.
Examples of base units include the meter for length, the kilogram for mass, the second for time, the ampere for electric current, the Kelvin for temperature, the mole for amount of substance, and the candela for luminous intensity. These units are defined based on natural phenomena and are universally recognized.
Derived units are created by combining base units using mathematical operations such as multiplication, division, and exponentiation. For example, the unit for speed is meters per second (m/s), which is derived from the base units of length and time. Other examples of derived units include the newton for force, the joule for energy, the watt for power, and the volt for electric potential.
Measurement units play a crucial role in science, engineering, and many other fields. They allow us to express physical quantities with precision and accuracy, making it possible to analyze, compare, and communicate complex data effectively.
The measurements which are given in question are most suitable for length of leaves.
To know more about length visit:
https://brainly.com/question/30537092
#SPJ1
You are given the function h(t) = ť – 4t + 2 - Find h(-2). Do not include "h(-2) =" in your answer.
Answers
Substituting these values in the given function, we get:
h(-2) = 4 + 8 + 2
Simplifying the expression further, we get:
h(-2) = 14
So, h(-2) is equal to 14.
The function h(t) = ť – 4t + 2 represents a quadratic equation in t, where t is the independent variable and h(t) is the dependent variable.
To find h(-2), we need to substitute -2 in place of t in the given function as follows:
h(-2) = (-2)^2 - 4(-2) + 2
Here, (-2)^2 means -2 multiplied by itself, which equals 4.
Also, -4(-2) means the product of -4 and -2, which equals 8.
Therefore, substituting these values in the given function, we get:
h(-2) = 4 + 8 + 2
Simplifying the expression further, we get:
h(-2) = 14
So, h(-2) is equal to 14.
Learn more about function from
https://brainly.com/question/11624077
#SPJ11
Miss Tyrrell catches the 9:45am bus from Leeds to London.
The distance between the two cities is 195 miles.
The bus travels at an average speed of 52 mph.
What time should she arrive in Glasgow?
Answers
Step-by-step explanation:
Give me the answer each one please.

At an ocean depth of 8 meters, a buoy bobs up and then down 5 meters from the ocean's depth. Sixteen seconds pass from the time
the buoy is at its highest point to when it is at its lowest point. Assume at x = 0 the buoy is at normal ocean depth.
Use the sine tool to graph the function. The first point must be on the midline and the second point must be a maximum or minimum
value on the graph closest to the first point.
Answers
Answer:
The answer is the equation for the function describing the movement of the buoy:
f(x) = 5 * sin(2 * pi * x / 16) + 8
Step-by-step explanation:
To graph the function, we need to find an equation that describes the buoy's movement. Since the buoy bobs up and down 5 meters from the ocean's depth, we can use the sine function. The amplitude of the function is 5, since the buoy moves 5 meters from the normal ocean depth. The period of the function is 16 seconds, since it takes 16 seconds for the buoy to go from its highest point to its lowest point.
Using this information, we can write the equation for the function as:
f(x) = 5 * sin(2 * pi * x / 16) + 8
where x is the time in seconds.
The first point on the graph would be (0, 8), since at x = 0 the buoy is at normal ocean depth. The second point would be either a maximum or minimum value on the graph closest to x = 0, which can be found by finding the derivative of the function and setting it equal to zero.
The graph of the function would look like a wave that oscillates up and down, with a maximum value of 5 meters above the normal ocean depth and a minimum value of 3 meters below the normal ocean depth.
isiaiisjjajsihajaihaiahshushsu a habja uahabja ha ha a ha ha Janna j Jabjaban an aka. na a ha ha ha ha a ja aja naja ha. ha aub ah ah ah ha ahahaha a ahba ahbahabhaba babav aha ha ha answer a
solution to 5y\9-y\9 is equal to 8\9?
Answers
Answer:
\(y = 2\)
Step-by-step explanation:
1) Simplify 5y/9 - y/9 to 4y/9.
\( \frac{4y}{9} = \frac{8}{9} \)
2) Multiply both sides by 9.
\(4y = \frac{8}{9} \times 9\)
3) Cancle 9.
\(4y = 8\)
4) Divide both sides by 4.
\(y = \frac{8}{4} \)
4) Simplify 8/4 to 2.
\(y = 2\)
Hence, the answer is y = 2.
Who can answer this?

Answers
Answer:
nonliner and linear c.
Step-by-step explanation:
kkkkkkkkkkkkkkkkkkkk
find the expected value of the proposition.round your answer to two decimal places. losses must be expressed as negative values.

Answers
To find the expected value of the question, we need to find the probability of having a card with a value less or equal to 5, and the probabilities greater than 5. We are told that the aces are considered the highest card in the deck. So, this card is not part of the group less or equal to 5.
Then, we have in a standard deck of cards 52 cards.
• Those cards that are equal or less than 5 are 16 cards.
,• Those cards that are greater than 5 are 36 cards.
The probability of having a card equal to or less than 5 is equal to:
\(P(C\leq5)=\frac{16}{52}\)The probability of having a card greater than 5 is equal to:
\(P(C>5)=\frac{36}{52}\)When we pay someone, we have a "loss" in a game. Then, if we pay $22, we need to write this value as -$22.
Therefore, the expected value of the proposition is as follows:
\(E(V)=\frac{16}{52}\cdot39-\frac{36}{52}\cdot22=-3.23076923077\)If we round the result to two decimal places, we have that the expected value is equal to E(V) = $ -3.23.

Find a point-slope form with slope 1/2 and passing through the point (-7,-1)
Answers
Answer:
x-2y+5=0
Step-by-step explanation:
y+1= \(\frac{x+7}{2}\)
y=\(\frac{x+7}{2}\) -1
y=\(\frac{x+7-2}{2}\)
y=\(\frac{x+5}{2}\)
2y=x+5
x-2y+5=0
The equation is:
⇨ y + 1 = 1/2(x + 7)Work/explanation:
Recall that the point slope formula is \(\rm{y-y_1=m(x-x_1)}\),
where m is the slope and (x₁, y₁) is a point on the line.
Plug in the data:
\(\rm{y-(-1)=\dfrac{1}{2} (x-(-7)}\)
Simplify
\(\rm{y+1=\dfrac{1}{2}(x+7)}\)
Hence, the equation in point slope is y + 1 = 1/2(x + 7).Write 27^2/9^4 as a power of 3
Answers
Answer: We can simplify 27 as 3^3 and 9 as 3^2. Then, we have:
27^2/9^4 = (3^3)^2/(3^2)^4
Using the power of a power rule, we can simplify:
= 3^(3x2)/(3^2x4)
= 3^6/3^8
Using the quotient rule, we can subtract the exponents:
= 3^(6-8)
= 3^-2
Therefore, 27^2/9^4 can be expressed as 3^-2 in terms of a power of 3.
brainliest???? (:
A friend of yours bought a new sports car with a $5,000 down payment plus a $28,000 car loan that is financed at an interest rate of 0.50% per month for 60 months. a. Calculate the required monthly loan payment on the car. b. How much does your friend still owe on the car loan immediately after she makes the 24 th monthly payment? c. If, after the 24th payment, she decides to pay $100 more each month, how many months will it take her to payoff the remaining loan she owes? a. The required monthly payment is (Round to the nearest cent.) b. Your friend still owes $ on the car loan. (Round to the nearest dollar.) c. It will take her months (Round-up to the nearest month)
Answers
(a) the required monthly loan payment on the car is approximately $528.23, (b)your friend still owes approximately $17,833.86 on the car loan after the 24th monthly payment, (c)it will take your friend approximately 23 months (rounded up to the nearest month) to pay off the remaining loan she owes after the 24th payment, given the increased monthly payment of $100.
(a) The required monthly loan payment on the car can be calculated using the formula for the monthly payment on a loan. Given a car loan of $28,000, financed at an interest rate of 0.50% per month for 60 months, the monthly payment can be determined using the following formula:
Monthly Payment = (Loan Amount * Monthly Interest Rate) / (1 - (1 + Monthly Interest Rate)^(-Number of Months))
Plugging in the values, we have:
Monthly Payment = (28000 * 0.005) / (1 - (1 + 0.005)^(-60))
Calculating this, the required monthly loan payment on the car is approximately $528.23.
(b) After making the 24th monthly payment, your friend still owes a remaining balance on the car loan. To calculate this, we need to determine the remaining balance based on the number of payments made and the original loan amount. We can use the formula:
Remaining Balance = Loan Amount * (1 + Monthly Interest Rate)^Number of Payments - (Monthly Payment * ((1 + Monthly Interest Rate)^Number of Payments - 1) / Monthly Interest Rate)
Plugging in the values, we have:
Remaining Balance = 28000 * (1 + 0.005)^24 - (528.23 * ((1 + 0.005)^24 - 1) / 0.005)
Calculating this, your friend still owes approximately $17,833.86 on the car loan after the 24th monthly payment.
(c) If your friend decides to pay $100 more each month after the 24th payment, we can calculate the number of months it will take her to pay off the remaining loan balance. Using the increased monthly payment, we can calculate the new remaining balance and divide it by the increased monthly payment to determine the number of months needed to pay off the loan.
New Remaining Balance = Remaining Balance - (Monthly Payment + Additional Monthly Payment) * ((1 + Monthly Interest Rate)^Number of Payments - 1) / Monthly Interest Rate
Number of Months = New Remaining Balance / (Monthly Payment + Additional Monthly Payment)
Plugging in the values, we have:
New Remaining Balance = 17,833.86 - (528.23 + 100) * ((1 + 0.005)^x - 1) / 0.005
Number of Months = New Remaining Balance / (528.23 + 100)
By solving the equation, it will take your friend approximately 23 months (rounded up to the nearest month) to pay off the remaining loan she owes after the 24th payment, given the increased monthly payment of $100.
Learn more about interest rate here:
https://brainly.com/question/12496793
#SPJ11
For Items 7-9, two relations are given. One relation is a function and one is not. Identify each and explain. 7. {(5,-2), (-2,5), (2, -5), (-5,2)} {(5,-2), (-2,5), (5,2), (-5, 2)}
Answers
#Relation 1 is a function, for each value of x, there is a corresponding value of Y. Also there's no element in the x, without corresponding values in Y.So this is a Function
1) The easiest way to make it, is by sketching it a diagram.
Let's do this
For the 1st Relation:
As we can see, for each value of x, there is a corresponding value of Y. Also there's no element in the x, without corresponding values in Y.So this is a Function
#2 Relation
Since for 5 there are 2 corresponding values this can't be a function. Because in a function one value in the domain can only relate to another only one value in the Range.


please help on this question

Answers
Answer:
B. 9
Step-by-step explanation:
the trapezoids are the same size so the length of AB is the same length of RS
Miriam packed 4 T-shirts, 3 pairs of shorts and two pairs of shoes for her vacation. How many different T-shirt, short and shoe outfit combinations can she wea
Answers
Answer:
24
Step-by-step explanation: