determine this is the function, the app is crashing
a) r'lt) b) T (1) c) r""(t) a r' (t) x r"(t).
a) r'lt) b) T (1) c) r""(t) a r' (t) x r"(t).
y(t) = (t, t^2, t^3)
"
Answers
All the values of the solution are,
a) r'(t) = (1, 2t, 3t²)
b) T(1) = (1/√14, 2/√14, 3/√14)
c) r''(t) = r'(t) x r''(t) = (6t, -3t, 2).
We have to given that,
The function is,
⇒ y(t) = (t, t², t³)
a) For r'(t), we need to take the derivative of r(t) = (t, t², t³) with respect to t:
r'(t) = (1, 2t, 3t²)
b) For T(1), we need to normalize r'(t) at t = 1:
r'(1) = (1, 2, 3)
||r'(1)|| = √(1 + 2 + 3) = √14
Therefore, T(1) = r'(1) / ||r'(1)|| = (1/√14, 2/√14, 3/√14)
c) For r''(t), we need to take the second derivative of r(t) with respect to t:
r''(t) = (0, 2, 6t)
Then, we can find r'(t) x r''(t) by taking the cross product:
r'(t) x r''(t) = (6t, -3t, 2)
Therefore, r''(t) = r'(t) x r''(t) = (6t, -3t, 2).
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ4
Related Questions
The area of a circle is 144π ft². What is the circumference, in feet? Express your answer in terms of \piπ.
Answers
Answer:
24π inches
Step-by-step explanation:
Area = π × r²
144π = π × r²
r² = 144
r = 12
Circumference = 2 π × r
= 2 × π × 12
= 24π in
Question: Erin needs of a cup of chocolate chips to make a cake and of a cup of chocolate chips for the frosting. She's trying to decide if a one cup bag of chocolate chips will be enough for the cake and the frosting. Determine whether Erin needs to buy more chocolate chips. es ) answer below: View Format - Table - hope someone can help
Answers
Answer:
She needs to buy more chocolate chips≥
Step-by-step explanation:
An easy question for people who want points
What is the MISSING NUMBER in the pattern?

Answers
Answer:
12 5/12 i think
Step-by-step explanation:
Answer:
13 3/10 is the answer.
need help asap very confusing (for me)

Answers
Answer:
The last one (2/3 and 8/12)
Step-by-step explanation:
When you reduce 8/12, you would get 2/3. If you multiply 2/3, you would get 8/12. Therefore, this ratio is proportional.
Have a good day :)
1-Find the cosine of the angle between A and B with respect to the standard inner product on M22 A = [2 1 6 -3] , B = [3 1 2 0]
Answers
The cosine of the angle between vectors A and B with respect to the standard inner product on M22 is √7 / 10.
This was determined by calculating the dot product of A and B, and dividing it by the product of their magnitudes.
To find the cosine of the angle between vectors A and B with respect to the standard inner product on M22, we can use the formula:
cos(theta) = (A·B) / (||A|| ||B||)
where A·B represents the dot product of A and B, and ||A|| and ||B|| represent the magnitudes of vectors A and B, respectively.
Let's calculate each component needed for the formula:
A·B = (2)(3) + (1)(1) + (6)(2) + (-3)(0) = 6 + 1 + 12 + 0 = 19
||A|| = sqrt((2^2 + 1^2 + 6^2 + (-3)^2) = sqrt(4 + 1 + 36 + 9) = sqrt(50) = 5√2
||B|| = sqrt((3^2 + 1^2 + 2^2 + 0^2) = sqrt(9 + 1 + 4 + 0) = sqrt(14)
Now, we can plug in these values into the formula:
cos(theta) = (A·B) / (||A|| ||B||) = 19 / (5√2 * √14)
To simplify further, we can rationalize the denominator:
cos(theta) = 19 / (5√28) = 19 / (5 * 2√7) = (19 / 10) * (1 / √7) = (19√7) / 10√7 = √7 / 10
Therefore, the cosine of the angle between vectors A and B with respect to the standard inner product on M22 is √7 / 10.
To learn more about standard inner product click here: brainly.com/question/32071888
#SPJ11
Which recursive formula correctly models the values shown in the table?
n 1 2 3 4 5
an 5 15 45 135 405
a. an+1=an+10, a1=5
b. an+1=an+5, a1=10
c. an+1=an⋅3, a1=5
d. an+1=an⋅5, a1=3
Answers
The right answers are
1. C, 1
2. B, an+1 = an x 3, a1 =5
3. C, an = -6 x 0.5^n-1
4. D, an + 2/3 x (1/2)^n-1
5. D, an+1 = an x (-2), a1 = 5
I just took the test and got 100% so these should be correct
An algorithm will be used to identify the maximum value in a list of one or more integers. Consider the two versions of the algorithm below. Algorithm I: Set the value of a variable max to - 1. Iterate through the list of integer values. If a data value is greater than the value of the variable max, set max to the data value. Algorithm II : Set the value of a variable max to the first data value. Iterate through the remaining values in the list of integers. If a data value is greater than the value of the variable max, set max to the data value. Which of the following statements best describes the behavior of the two algorithms? A Both algorithms work correctly on all input values. В Algorithm I always works correctly, but Algorithm II only works correctly when the maximum value is not the first value in the list. Algorithm Il always works correctly, but Algorithm I only works correctly when the maximum value is greater than or equal to - 1. D Neither algorithm will correctly identify the maximum value when the input contains both positive and negative input values.
Answers
Algorithm Il always works correctly, but Algorithm I only works correctly when the maximum value is greater than or equal to - 1
=====================================================
Explanation:
Let's say we have the data set {-4,-3,-2}. The value -2 is the largest.
If we follow algorithm 1, then the max will erroneously be -1 after all is said and done. This is because the max is set to -1 at the start even if -1 isn't in the data set. Then we see if each data value is larger than -1.
-4 > -1 is false-3 > -1 is false-2 > -1 is falseEach statement being false means we do not update the max to its proper value -2. It stays at -1.
This is why we shouldn't set the max to some random value at the start.
It's better to use the some value in the data set to initialize the max. Algorithm 2 is the better algorithm. Algorithm 1 only works if the max is -1 or larger.
A cylinder tank has a radius of 7.5 feet and an altitude of 14 feet. If a gallon of paint will cover 130 ft.² of surface how much paint is needed to put two coats of paint on the entire surface of the tank?
Answers
A cylinder tank has a radius of 7.5 feet and an altitude of 14 feet. If a gallon of paint will cover 130 ft.² of surface how much paint is needed to put two coats of paint on the entire surface of the tank?
Remember that
The surface area of a cylinder is equal to
\(SA=2B+Ph\)where
B is the area of the circular nase
P is the circumference of the circular base
h is the height of the cylinder
so
Find out B
\(B=\pi\cdot r^2\)we have
r=7.5 ft
pi=3.14
substitute
\(\begin{gathered} B=3.14\cdot(7.5)^2 \\ B=176.625\text{ ft2} \end{gathered}\)Find out the circumference
\(\begin{gathered} P=2\pi\cdot r^{} \\ P=2(3.14)\cdot7.5 \\ P=47.1\text{ ft} \end{gathered}\)the value of h=14 ft
therefore
SA=2(176.625)+47.1(14)
SA=1,012.65 ft2
Remember that s needed to put two coats of paint
Multiply the surface area by 2
1,012.65*2=2,025.3 ft2
1 gallon -------> 130 ft2
applying proportion
1/130=x/2,025.3
solve for x
x=2,025.3/130
x=15.6 gal
therefore
the answer is 16 gallon9x+10=11x-10
Please show work
Answers
Answer:
\(x=10\)
Step-by-step explanation:
1) Subtract 10 from both sides of the equation
\(9x+10=11x-10\\9x+10-10=11x-10-10\)
2) Simplify
a. Subtract the numbers
b. Subtract the numbers again
\(9x=11x-20\)
3) Subtract 11x from both sides of the equation
\(9x=11x-20\\9x-11=11x-20-11x\)
4) Simplify
a. Combine like terms
b. Combine like terms again
\(-2x=-20\)
5) Divide both sides of the equation by the same term
\(-2x=20\\\frac{-2x}{-2} =\frac{-20}{-2}\)
6) Simplify
a. Cancel terms that are in both the numerator and denominator
\(\frac{-2x}{-2} =\frac{-20}{-2} \\x=\frac{-20}{2}\)
b. Divide the numbers
\(x=\frac{-20}{-2x} \\x=10\)
9x + 10 = 11x + -10
Reorder the terms:
10 + 9x = 11x + -10
Reorder the terms:
10 + 9x = -10 + 11x
Solving
10 + 9x = -10 + 11x
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-11x' to each side of the equation.
10 + 9x + -11x = -10 + 11x + -11x
Combine like terms: 9x + -11x = -2x
10 + -2x = -10 + 11x + -11x
Combine like terms: 11x + -11x = 0
10 + -2x = -10 + 0
10 + -2x = -10
Add '-10' to each side of the equation.
10 + -10 + -2x = -10 + -10
Combine like terms: 10 + -10 = 0
0 + -2x = -10 + -10
-2x = -10 + -10
Combine like terms: -10 + -10 = -20
-2x = -20
Divide each side by '-2'.
x = 10
Simplifying
x = 10
A student tosses a six-sided die, with each side numbered 1 though 6, and flips a coin. What is the probability that the die will land on the face numbered 1 and the coin will land showing tails? A. 1/3 B. 1/12 C. 1/6 D. 1/4
Answers
The probability that the die will land on the face numbered 1 and the coin will land showing tails is 1/12.In the offered options, this corresponds to option B.
There are two events happening here: the die being rolled and the coin being flipped. Since these events are independent, we can find the probability of both events occurring by multiplying the probabilities of each individual event.
The probability of rolling a 1 on a six-sided die is 1/6, and the probability of flipping tails on a coin is 1/2. We multiply these probabilities to obtain the likelihood of both occurrences occurring.:
1/6 x 1/2 = 1/12
Therefore, the probability that the die will land on the face numbered 1 and the coin will land showing tails is 1/12. In the offered options, this corresponds to option B.
It is important to note that the probabilities of the two events are independent, meaning that the outcome of one event does not affect the outcome of the other event
Learn more about probabilities
https://brainly.com/question/30034780
#SPJ4
Let E be the elliptic curve y^2 = x^3+2x +7 defined over Z31. It can be shown that #E = 39 and P = (2, 9) is an element of order 39 in E. The Simple Elliptic Curve-Based Cryptosystem defined on E has Z31* as a plaintext space. Suppose the private key is m = 8.(a.) Compute Q = mP.(b.) Decrypt the following string of ciphertext:((18, 1), 21), ((3, 1), 18), ((17, 0), 19) ((28, 0), 8).(c.) Assuming that each plaintext represents one alphabetic character, convert the plaintext into an English word. (Here we will use the correspondence A ßà1, . . . , Zßà26, because 0 is not allowed in a (plaintext) ordered pair.)
Answers
(a) To compute Q = mP, where P = (2, 9) and m = 8, we perform scalar multiplication on the elliptic curve. Starting with P, we double it seven times since m is 8 in binary representation: P, 2P, 4P, 8P, 16P, 32P, 64P. Since the order of E is 39, we can reduce the points modulo 39 at each step. The final result is Q = (4, 5).
(b) To decrypt the given ciphertext, we need to find the inverse of the private key m modulo 39. In this case, 8^(-1) ≡ 8 (mod 39). We compute the scalar multiplication of each ciphertext point with Q: C1 = 8^(-1)((18, 1) - (4, 5)), C2 = 8^(-1)((3, 1) - (4, 5)), C3 = 8^(-1)((17, 0) - (4, 5)), and C4 = 8^(-1)((28, 0) - (4, 5)). Reducing the resulting points modulo 39, we get C1 = (22, 21), C2 = (28, 26), C3 = (0, 17), C4 = (24, 23).
(c) Assuming each plaintext represents one alphabetic character, we can convert the ciphertext points (x, y) to their corresponding letters by adding 1 to the x-coordinate to obtain the position in the alphabet. Converting the ciphertext points to letters, we have C1 = "VU", C2 = "BZ", C3 = "RC", and C4 = "XW". Therefore, the English word decrypted from the given ciphertext is "VUBZRCXW
Learn more about scalar multiplication here:
https://brainly.com/question/30221358
#SPJ11
NEED THIS ASAP 50 POINTS UWU
Which property of equality should you apply to keep the equation 22 . a = 242 in balance when solving?
The division property of equality
The subtraction property of equality
The reflexive property
The substitution property of equality
Answers
A property of equality that you should apply to keep the equation 22 . a = 242 in balance when solving include the following: A. The division property of equality.
What is the subtraction property of equality?In Mathematics and Geometry, the subtraction property of equality states that the two (2) sides of an algebraic expression or equation would still remain equal even when the same number has been subtracted from both sides of an equality.
Based on the information provided above, we can logically deduce the following equation:
22 . a = 242
22 × a = 242
By applying the division property of equality, we have the following:
a = 242/22
a = 11.
Read more on subtraction property of equality here: brainly.com/question/16993368
#SPJ1
A pump fills a pool at a constant rate. At the end of 1 minute, it has filled 10 gallons of water. Which table represents the relationship between the number of minutes and the number of gallons of water in the pool?
A
\text{Time} \newline \text{ (minutes)}Time
(minutes) \text{Water} \newline \text{ (gallons)}Water
(gallons)
22 2020
44 4040
66 6060
B
\text{Time} \newline \text{ (minutes)}Time
(minutes) \text{Water} \newline \text{ (gallons)}Water
(gallons)
11 1010
22 3030
44 5050
C
\text{Time} \newline \text{ (minutes)}Time
(minutes) \text{Water} \newline \text{ (gallons)}Water
(gallons)
22 2020
44 2222
66 2424
D
\text{Time} \newline \text{ (minutes)}Time
(minutes) \text{Water} \newline \text{ (gallons)}Water
(gallons)
11 1010
22 1111
44 1313
I'm sorry this is confusing :\

Answers
The answer is A, because if one minute corresponds to 10 gallons of water, then the amount of gallons is the minutes times 10.
Can someone help me with these two!!!

Answers
Answer:
1. is 130 times taller
2. is 0.756 kilograms
Step-by-step explanation:
for 1, you divide 65 by 0.5 or multiply it by 1/2
for 2, you divide 756 by 1000
Find the equation of the line parallel to y = 2x - 4 that runs through the point (-2, 4).
Answers
Answer:
y = 2x + 8
Step-by-step explanation:
Equation of line:Parallel lines have same slope.
y = 2x - 4
Slope = 2
Point (-2 ,4)
Equation of line in point-slope form:
y - y₁ = m(x - x₁)
y - 4 = 2(x - [-2] )
y - 4 = 2(x + 2)
y -4 = 2x + 4
y = 2x + 4 + 4
\(\sf \boxed{y = 2x + 8}\)
100points! At the hardware store, you purchase a box of nails originally worth $14.99. You have a coupon for 20% off the nails. Sales tax is 6%. What is the total cost for the nails?
Must show work!
Answers
Answer:
$4.80
Step-by-step explanation:
First, apply the coupon to the original price
20% of 14.99 = 2.998
or
0.20 x 14.99 = 2.998
Then, find the sales tax of the new price
%6 of 2.998 = 1.7988
or
0.60 x 2.998 = 1.7988
Finally, add the sales tax to the new price
2.998 + 1.7988 = 4.7968
Round 4.7968 to the nearest tenth to get 4.80
Hope this helped!
Total cost
\(\\ \sf\longmapsto 14.99-0.14(14.99)\)
\(\\ \sf\longmapsto 14.99-2.09\)
\(\\ \sf\longmapsto 12.9\$\)
Done
for the following equilibrium, if ksp=5.8×10−24, what is the molar solubility of scandium fluoride:
Answers
The molar solubility of scandium fluoride can be calculated using the solubility product constant (Ksp) and stoichiometry. The molar solubility is approximately 7.61 × 10^(-9) mol/L.
The solubility product constant (Ksp) is an equilibrium constant that represents the equilibrium between a solid compound and its dissociated ions in a saturated solution.
For scandium fluoride (ScF3), the equilibrium can be represented as follows:
ScF3 (s) ⇌ Sc³⁺ (aq) + 3F⁻ (aq)
The solubility product expression for this equilibrium is:
Ksp = [Sc³⁺][F⁻]³
Given that the Ksp value for scandium fluoride is 5.8 × 10^(-24), we can use this information to calculate the molar solubility.
Step 1: Assign variables to the molar solubility.
Let x represent the molar solubility of ScF3 in mol/L.
Step 2: Write the equilibrium expression.
Since the stoichiometry of the reaction is 1:3, the equilibrium expression becomes:
Ksp = (x)(3x)³ = 27x⁴
Step 3: Substitute the Ksp value and solve for x.
Plugging in the Ksp value of 5.8 × 10^(-24), we have:
5.8 × 10^(-24) = 27x⁴
Step 4: Solve for x.
Taking the fourth root of both sides, we get:
x⁴ = (5.8 × 10^(-24))/27
x⁴ ≈ 7.61 × 10^(-26)
Taking the square root of both sides, we find:
x ≈ 7.61 × 10^(-9) mol/L
Therefore, the molar solubility of scandium fluoride is approximately 7.61 × 10^(-9) mol/L.
In summary, by using the solubility product constant (Ksp) and stoichiometry, we can calculate the molar solubility of scandium fluoride. In this case, the molar solubility is approximately 7.61 × 10^(-9) mol/L, indicating that scandium fluoride has a very low solubility in water.
To learn more about equilibrium, click here: brainly.com/question/1915798
#SPJ11
Find the next two terms of each sequence.
1.) -16, 8, -4, 2, ...
2.) 1, 4, 9, 16, 25, ...
Answers
Answer:
1)=-1;1
2)=36;49
Step-by-step explanation:
1.)aqui la secuncia es dividir en -2
2.)aqui la secuencia es sumar numeros impares es decir:+3;+5;+7 etc
Train A has a speed 30 miles per hour greater than that of train B. If train A travels 210 miles in the same times train B travels 120 miles, what are the speeds of the two trains
Answers
The speed of train B is 60 miles per hour, and the speed of train A is 90 miles per hour.
To determine the speeds of trains A and B, we can set up a proportion based on the given information. Let's assume the speed of train B is x miles per hour. According to the problem, train A's speed is 30 miles per hour greater than that of train B, so train A's speed can be represented as (x + 30) miles per hour.
Now, we can set up a proportion based on the distances traveled by the two trains. The distance traveled by train A is 210 miles, and the distance traveled by train B is 120 miles. The proportion can be written as:
x/120 = (x + 30)/210
To solve this proportion, we can cross-multiply and solve for x:
210x = 120(x + 30)
210x = 120x + 3600
90x = 3600
x = 40
Therefore, the speed of train B is 40 miles per hour. Since train A's speed is 30 miles per hour greater, train A's speed is 40 + 30 = 70 miles per hour.
Learn more about speed
brainly.com/question/17661499
#SPJ11
Sonya borrowed 2 fewer than twice the number of books that
Roberto borrowed. Sonya borrowed 14 books. How many books
did Roberto borrow?
F. 2 books G. 4 books H. 8 books J. 12 books
Answers
Roberto borrowed 8 book according to the case information. Option H is correct.
According to the problem, Sonya borrowed 2 fewer than twice the number of books that Roberto borrowed, and we know Sonya borrowed 14 books.
Let's denote the number of books Roberto borrowed as R. Then, according to the problem, Sonya's books can be calculated as 2R - 2.
Setting that equal to the 14 books Sonya borrowed gives us the equation:
2R - 2 = 14
Adding 2 to both sides of the equation gives us:
2R = 16
Dividing both sides by 2 gives us:
R = 16/2
R = 8
Therefore, Roberto borrowed 8 books, which corresponds to option H.
Learn more about equation https://brainly.com/question/14686792
#SPJ11
Find the volume of the cylinder. Use 3.14 for Tr.
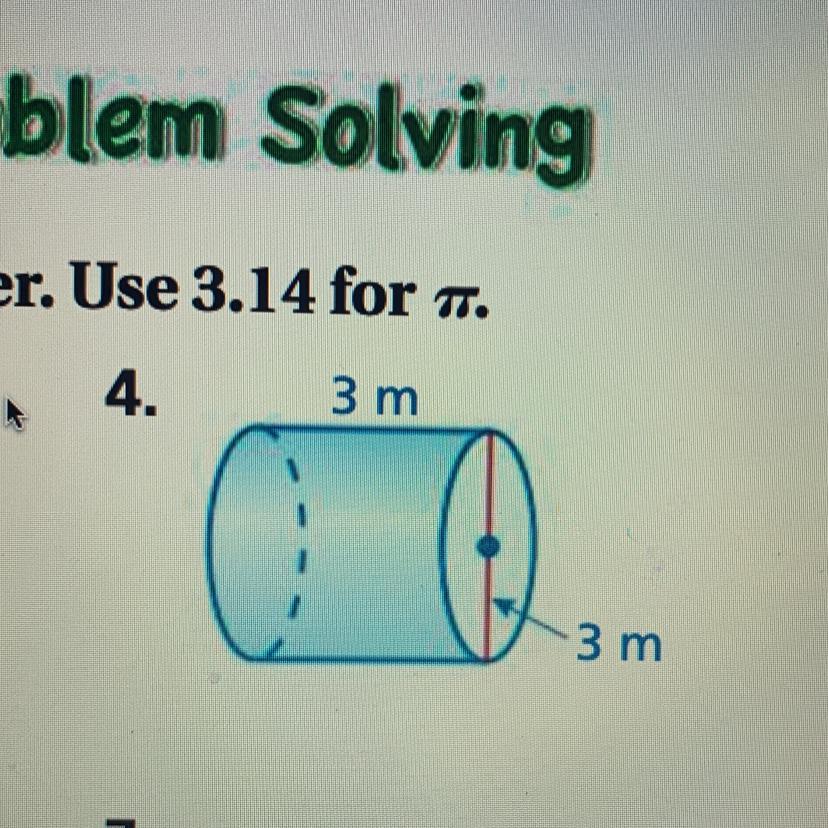
Answers
Answer:
area = 42.41
a=2nrh×2nr²
a=2(3.14)(1.5)(3)+2×3.14×1.5²
a=42.41
find the taylor series for f centered at 9 if f (n)(9) = (−1)nn! 3n(n 1) . [infinity] n = 0 what is the radius of convergence r of the taylor series? r =
Answers
The Taylor series for f (n)(9) = (−1)nn! 3n(n 1) centered at 9 is ∑[n=0 to ∞] (-1)ⁿ 3ⁿ (x-9)ⁿ (ⁿ+¹).
Using Taylor's formula with the remainder in Lagrange form, we have
f(x) = ∑[n=0 to ∞] (fⁿ(9)/(n!))(x-9)ⁿ + R(x)
where R(x) is the remainder term.
Since fⁿ(9) = (-1)^n n!(n+1)3ⁿ, we have
f(x) = ∑[n=0 to ∞] (-1)ⁿ 3ⁿ (x-9)ⁿ (n+1)
To find the radius of convergence, we use the ratio test:
lim[n→∞] |(-1)ⁿ 3(ⁿ+¹) (ⁿ+²)/(ⁿ+¹) (ˣ-⁹)| = lim[n→∞] 3|x-9| = 3|x-9|
Therefore, the series converges if 3|x-9| < 1, which gives us the radius of convergence:
r = 1/3
So the Taylor series for f centered at 9 is
f(x) = ∑[n=0 to ∞] (-1)ⁿ 3ⁿ (x-9)ⁿ (ⁿ+¹)
and its radius of convergence is r = 1/3.
Learn more about taylor series : https://brainly.com/question/23334489
#SPJ11
Determine the function that is the inverse of f(x)=2**(x-1) .
Answers
The inverse function of f(x) = \(2^(x-1)\) is \(f^(-1)(x)\) = log2(x) + 1. The inverse function takes an input x and returns the value y, such that when y is plugged back into the original function, we obtain the original input x.
The inverse function of f(x) = \(2^(x-1)\) is given by \(f^(-1)(x)\) = log2(x) + 1, where log2(x) represents the logarithm base 2 of x.
To find the inverse function, we need to interchange the roles of x and y in the original function and solve for y. Let's start with f(x) = \(2^(x-1)\) and rewrite it as y = \(2^(x-1)\).
Step 1: Interchange x and y: x = \(2^(y-1)\).
Step 2: Solve for y: Taking the logarithm base 2 of both sides, we get log2(x) = y - 1.
Step 3: Isolate y: Adding 1 to both sides, we obtain y = log2(x) + 1.
Therefore, the inverse function of f(x) = \(2^(x-1)\) is \(f^(-1)(x)\) = log2(x) + 1. The inverse function takes an input x and returns the value y, such that when y is plugged back into the original function, we obtain the original input x.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
Determine if the sides are greater than (>), less than (<), or equal (=) to each other.
REFER TO ATTACHMENT! Best answer will be given brainliest. fake answers will be reported and deleted. <3
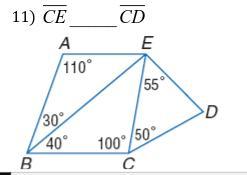
Answers
Answer:
\(\sf{ \bar{BC}} = \sf{ \bar{EC}}\)
Explaination:
\(\sf \angle EBC = 40 \degree \: ..(given) \\\sf \angle EBC + \angle \: CEB + \angle BCE = 180 \degree \\ \sf 40 + \angle \: CEB + 100 = 180 \: \\ \sf ..(sum \: of \: measure \: of \: all \: angles \: of \: triangle \\ \sf \angle \: CEB + 140 = 180 \\\angle \: \sf \: CEB = 180 - 140 \\ \sf \: \angle \: CEB = 40 \degree \\ \\ \sf \therefore \: \angle EBC = \angle \: CEB \\ \sf \: In \:triangle \: sides \: opposite \: to \: congruent \: angles \: are \: congruent \\ \therefore \: \sf{ \bar{BC}} = \sf{ \bar{EC}}\)
\( \sf \pink{hope \: it \: helps :)}\)
Identify whether or not the following features are represented in the above diagram for each feature that is represented write the name(s) denoted it in the diagram

Answers
The geometric features of objects are the objects features that are constructed by the aid of elements of geometry
The definition of the geometrical features are as follows
A ray is a line having a single starting point and a straight extension, having no end pointA vertex is the meeting point of two or more linesAn angle is formed by two rays that have a common vertexParallel lines are two lines that are always the same distance from each otherParallel planes are two planes that have equal distance from each otherCoplanar points are points on the same planeCollinear points are points on the same lineSegment addition postulate states that segment AC can include a third point B, when AB + BC = ACPerpendicular lines are two lines that intersect at 90°
Based on the above definitions, the values in the table are as follows;
\(\begin{array}{lcl} \mathbf{Feature}&& \mathbf{Denoted \ in \ diagram (s)}\\ \\Ray&&\\\\Vertex&&\\\\Angle&&\\\\Parallel \ lines &&\\\\Parallel \ planes &&\\\\Coplanar \ points&&\mathbf{C, \ F, A, N, B}\\\\Collinear \ points&&\mathbf{A, N, B}\\\\Segment \ addition \ postulate&&\mathbf{AN + NB} = AB\\\\Perpendicular \ lines&&\end{array}\right]\)
The features in the diagram are;
Coplanar points: C, F, A, N, B
Collinear points: A, N, B
Segment addition postulate: AN + NB = AB
Learn more about geometric features here:
https://brainly.com/question/11672333
wich is greater 4\10 or 32\10 explain how u know·
Answers
Answer:
32/10
Step-by-step explanation:
simplify them
4/10= 2/5= 0.4 (as a decimal)
32/10= 3.2 (as a decimal)
3.2>0.4
CAN SOMEONE LS HELP WITHT THIS ASAP PLEASE

Answers
Answer:
x = 10
y = 20
Step-by-step explanation:
Hope this hepls you.

Raven made 5 litres of fresh pineapple juice and 8 trays of croissants. He shared the juice with his 12 Friends
Answers
To find out how much juice each friend received, we need to divide the total amount of juice (5 liters) by the number of friends (12).
Each friend would receive 5/12 liters of juice. As for the croissants, we don't have enough information to determine how many croissants each friend received since the number of croissants in each tray is not specified. If Raven made 5 liters of fresh pineapple juice and shared it with 12 friends, we can calculate how much juice each friend received by dividing the total amount of juice by the number of friends.
Learn more about divide here;
https://brainly.com/question/15381501
#SPJ11
an inequity that can be written in the form ax by < c (where a and b are not both zero) is called a ____?____ inequality in two variables.
Answers
An inequality that can be written in the form ax + by < c (where a and b are not both zero) is called a linear inequality in two variables.
An inequality that represents a line in a two-dimensional coordinate system is referred to as a linear inequality. The set of points that satisfies the inequality is a half-plane bounded by a line that may be dashed or solid.
In contrast to a linear equation, which represents a line, a linear inequality represents a half-plane. The points on one side of the line, rather than the points on the line, are solutions to the inequality.
The method of shading is used to graph a linear inequality in two variables. First, graph the boundary line, which is usually represented by a solid or dashed line, and then select a test point on one side of the line. Shaded regions of the half-plane containing the test point satisfy the inequality.
Learn more about linear inequality here: https://brainly.com/question/30440630
#SPJ11
Shelley had 53¢ until she spent 1 quarter. How much money does Shelley have now?
Answers
Answer:
28¢
Step-by-step explanation:
A quarter is 25¢, so 53¢ - 25¢ = 28¢.