Answers
Answer:
Domain: \(\mathbb{N}\)Range: \(\mathbb{N}\)Step-by-step explanation:
The domain is the set of x values and the range is the set of y-values.
Related Questions
Suppose we want to choose letters, without replacement, from distinct letters. (a) If the order of the choices does not matter, how many ways can this be done? (b) If the order of the choices matters, how many ways can this be done?
Answers
The number of ways to choose 6 letters from a set of 13 is given as follows:
a) Order does not matter: 1716.
b) Order matters: 1,235,520.
When to use permutation and when to use combination?A combination is used when the order does not matter, hence, for item a, the number of ways is obtained as follows:
C(13,6) = 13!/(6!7!) = 1716.
A permutation is used when the order matters, hence, for item b, the number of ways is obtained as follows:
P(13,6) = 13!/7! = 1,235,520.
More can be learned about permutations and combinations at https://brainly.com/question/11732255
#SPJ1
If the rvalue, or correlation coefficient, of a data set is negative, the
coefficient of determination is negative.
Answers
The given statement is false. Because If the r-value, or correlation coefficient, of a data set, is negative, the coefficient of determination is positive.
What exactly does a negative correlation coefficient mean?Two variables with a negative correlation tend to move in opposing directions.
While a correlation value of -0.3 or below shows a very weak association, one of -0.8 or lower suggests a significant negative relationship.
The complete question is;
"The given statement is true or false
If the r-value, or correlation coefficient, of a data set, is negative, the coefficient of determination is negative."
Because If a data set's r-value, or correlation coefficient, is negative, the coefficient of determination is positive.
Hence, the given assertion is incorrect.
To learn more about the correlation refer to:
https://brainly.com/question/6563788
#SPJ1
Please see screenshot

Answers
The graph of the feasible region is attached
How to determine the graph of the feasible regionFrom the question, we have the following parameters that can be used in our computation:
\(\left\{ \begin{array}{lr} y + 7x \ge 10 \\ 8y + 2x \ge 20 \\ y + x \ge 4 \\ y + x\le 10 \\ x \ge 0 \\ y \ge 0\end{array}\)
To plot the graph of the feasible region, we plot each inequality in the domain x ≥ 0 and y ≥ 0
Using the above as a guide, the graph is attached
Read more about feasible region at
https://brainly.com/question/29084868
#SPJ1

Solve for x. Round to the nearest tenth, if necessary.

Answers
Answer:
10.7
Step-by-step explanation:
Since this is a right triangle, we can use trig functions to calculate the hypotenuse.
We know the opposite side from the angle labeled 59 degrees.
sin 59 = opp side / hypotenuse
sin 59 = 9.2/x
x = 9.2/ sin 59
x = 10.733
plzzzzzzzzz help
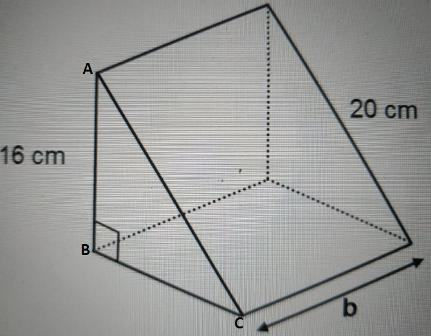
Volume of the following triangular prism is 960 cm3…
a) Determine the length of the base of the triangle.
b) Determine the area of the triangle.
help plz

Answers
Answer:
Step-by-step explanation:
a). By applying Pythagoras theorem in right triangle ABC,
AC² = AB² + BC²
20² = 16² + BC²
BC = \(\sqrt{400-256}\)
= 12
Therefore, another leg of the triangular base = 12 cm
Area of the triangular base ABC = \(\frac{1}{2}(\text{Base})(\text{Height})\)
= \(\frac{1}{2}(16)(12)\)
= 96 cm²
Volume of a triangular prism = Area of the triangular base × height
960 = 96 × b
b = 10 cm
b). Area of the triangle ABC = 96 cm²
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
A rocket is launched in the air. The graph below shows the height of the rocket hh in meters after tt seconds.
help pls

Answers
Answer:
The answers are=
(38, 0)time in seconds(19, 1768.9)Heightin metersThe x-coordinate of the vertex is (38, 0) and the y-coordinate of the vertex is (19, 1768.9).
What is a parabola?It is defined as the graph of a quadratic function that has something bowl-shaped.
(x - h)² = 4a(y - k)
(h, k) is the vertex of the parabola:
a = √[(c-h)² + (d-k²]
(c, d) is the focus of the parabola:
It is given that:
The graph of the parabolic path is shown in the picture.
From the graph:
The x-coordinate of the vertex is (38, 0)
The x-coordinate represents time in seconds
The y-coordinate of the vertex is (19, 1768.9)
The y-coordinate represents the height in meters
Thus, the x-coordinate of the vertex is (38, 0) and the y-coordinate of the vertex is (19, 1768.9).
Learn more about the parabola here:
brainly.com/question/8708520
#SPJ2
A population of rare birds in town is currently listed at 2,000. It is declining at a rate of 2% per year. How many birds will be left after 20 years? Round your answer to the nearest whole number.
A. 1,335 birds
B. 1,980 birds
C. 2,972 birds
D. 23 birds
Answers
Option(A) is the correct answer is A. 1,335 birds.
To calculate the number of birds that will be left after 20 years, we need to consider the annual decline rate of 2%.
We can use the formula for exponential decay:
N = N₀ * (1 - r/100)^t
Where:
N is the final number of birds after t years
N₀ is the initial number of birds (2,000 in this case)
r is the annual decline rate (2% or 0.02)
t is the number of years (20 in this case)
Plugging in the values, we get:
N = 2,000 * (1 - 0.02)^20
N = 2,000 * (0.98)^20
N ≈ 2,000 * 0.672749
N ≈ 1,345.498
Rounded to the nearest whole number, the number of birds that will be left after 20 years is 1,345.
for similar questions on population.
https://brainly.com/question/30396931
#SPJ8
Explain why the expression 10 to the power of zero, one to the power of four and 1×1.0 to the power of zero have the same value
Answers
Answer:
10*0=1, according to the law of indices which states that anything to the zero power is equal to one
1*4=1×1×1×1=1
1×1.0=1.0=1
The measure of angle Y is 4The measure of angle Y is 45°, and the measure of angle Z is 70°5°, and the measure of angle Z is 70°
What is the measure of angle W?
25°
65°
115°
120°
Answers
The sides of parallelogram ABCD are represented as shown.
5x – 18
3x-6
2x + 12
solve for x
solve for DA

Answers
From the given parallelogram:
a) x equals 10
b) The length of side DA is approximately 51.64.
How to find the lengths of the side of the parallelogram?a) We first solve for x, using the fact that opposite sides of a parallelogram are equal in length. Thus:
AB = CD, which gives us:
5x - 18 = 2x + 12
3x = 30
x = 10
b) To solve for DA, we need to use the formula for the area of a parallelogram:
Area = base × height
Since opposite sides of a parallelogram are parallel, its height is the perpendicular distance between AB and CD.
Let E be the point on CD such that AE is perpendicular to CD. Then, we have:
AE = CD sin(∠C)
AE = (2x + 12) sin(∠C)
Also, we have:
BE = AB sin(∠C)
BE = (5x - 18) sin(∠C)
Since AE = BE, we have:
(2x + 12) sin(∠C) = (5x - 18) sin(∠C)
2x + 12 = 5x - 18
3x = 30
x = 30/3
x = 10
Therefore, AE = BE = 2x + 12 = (2*10) + 12 = 32
The base of the parallelogram is AB = 5x - 18 = 5*10 - 18 = 32
So, the area of the parallelogram is:
Area = base × height
Area = AB × AE
Area = 32 × 32
Area = 1024
Finally, we can use the formula for the length of a diagonal of a parallelogram:
DA² = AB² + AD² - 2AB × AD cos(∠A)
The opposite angles of a parallelogram are equal, so, we have:
∠A = ∠C
cos(∠A) = cos(∠C)
cos(∠A) = (2x + 12) / AE
cos(∠A) = (2x + 12) / 32
Substituting x = 10, we get:
cos(∠A) = 11/16
Thus, we get:
DA² = (5x - 18)² + (2x + 12)² - 2(5x - 18)(2x + 12) cos(∠A)
DA² = (32)² + (52)² - 2(32)(52)(11/16)
DA² ≈ 2668.06
DA = √(2668.06)
Therefore, the length of DA is ≈ 51.64
Learn more about a parallelogram at brainly.com/question/970600
#SPJ1
help me I'm desperate I'm begging you please I'm about to break down help

Answers
a thief uses a bag of sand to replace a gold statue that sits on a weight-sensitive, alarmed pedestal. the bag of sand and the statue have exactly the same volume, 1.90 ll. (assume that the mass of the bag is negligible.) part a calculate the mass of each object. (densityofgold
Answers
4.65 kg the mass of each item (assuming the bag's mass is negligible). (Sand density is 3.00 g/cm3, while the density of gold is 19.3 g/cm3)
Given that,
A gold statue that is perched on a pedestal with a weight-sensitive alarm is replaced by a thief using a bag of sand. The statue and the bag of sand have the exact same volume, 1.55 L.
We have to calculate the mass of each item (assuming the bag's mass is negligible). (Sand density is 3.00 g/cm3, while the density of gold is 19.3 g/cm3)
We know that,
Mass of gold = Volume × Density
= 1.55×1000 cc × 19.3
= 29915 grams
= 29.915 Kg
Mass of sand = 1.55×1000×3
= 4650g
= 4.65 Kg
Volume = 1.55 L
= 1.55 × 1000 cc
= 1550 cc
Mass = Volume × Density
Mass of gold = 1550 × 19.3
= 29915 grams
= 29.915 kg
Mass of sand = 1550 × 3
= 4650 grams
= 4.65 kg
Therefore, 4.65 kg the mass of each item (assuming the bag's mass is negligible). (Sand density is 3.00 g/cm3, while the density of gold is 19.3 g/cm3)
To learn more about mass visit: https://brainly.com/question/16940422
#SPJ4
what is the property of 3x(5x7)=(3x5)7
Answers
The property you are referring to is called the associative property of multiplication. According to this property, when multiplying three numbers, the grouping of the numbers does not affect the result. In other words, you can change the grouping of the factors without changing the product.
In the equation you provided: 3x(5x7) = (3x5)7
The associative property allows us to group the factors in different ways without changing the result. So, whether we multiply 5 and 7 first, or multiply 3 and 5 first, the final product will be the same.
A function g(x) is defined as shown
2 + 3x,
OS X <4
g(x) = 0.5% + 10, 45 x < 8
16, b
X2B
What is the value of g(4)?
10
12
14
16

Answers
Answer:
12
Step-by-step explanation:
Take the equation where the interval < or = 4
g(4)= 0.5(4)+10
=2+10
=12
each function
f(x)=-4x-5;
ion for
Find ƒ(1)
for the given
Answers
When x is equal to 1, the Function f(x) = -4x - 5 yields a value of -9.
The find ƒ(1) for the function f(x) = -4x - 5, we need to substitute x = 1 into the function and evaluate the expression.
Replacing x with 1, we have:
ƒ(1) = -4(1) - 5
Simplifying further:
ƒ(1) = -4 - 5
ƒ(1) = -9
Therefore, when x is equal to 1, the value of the function f(x) = -4x - 5 is ƒ(1) = -9.
Let's break down the steps taken to arrive at the solution:
1. Start with the function f(x) = -4x - 5.
2. Replace x with 1 in the function.
3. Evaluate the expression by performing the necessary operations.
4. Simplify the expression to obtain the final result.
In this case, substituting x = 1 into the function f(x) = -4x - 5 gives us ƒ(1) = -9 as the output.
It is essential to note that the notation ƒ(1) represents the value of the function ƒ(x) when x is equal to 1. It signifies evaluating the function at a specific input value, which, in this case, is 1.
Thus, when x is equal to 1, the function f(x) = -4x - 5 yields a value of -9.
For more questions on Function .
https://brainly.com/question/11624077
#SPJ8
Estimate 6,976 + 3,983 + 13,560 by first rounding each number to the nearest thousand.
Answers
Answer:
Step-by-step explanation:
The thousand mark is the 4th number when going from right to left. So it would be the {6},976. When it comes to rounding, you go "5 and above, give it a shove, 4 and below, let it go. 6,976 rounded to the nearest thousand is 7,000, 3,983 rounded to the nearest thousand is 4,000, 13,560 rounded is 14,000.
7,000 + 4,000+ 14,000 = 25,000
how many pencils measure more than 5 1/2 inches but less than 7 2/4 inches
Answers
There are 7 pencils measuring more than 5 1/2 inches but less than 7 2/4 inches.
What is Inch?An inch is a unit of length in the imperial and US customary systems of measurement. Equal to 1/12 of a foot, it is usually denoted by the symbol "in". It is also equal to 2.54 centimeters. The inch is commonly used in the construction industry, engineering, and other fields.
To answer this question, we must first convert all of the measurements into the same unit of length. We will convert 5 1/2 inches and 7 2/4 inches into decimals by dividing the fractions by their denominators. 5 1/2 inches is equal to 5.5 inches and 7 2/4 inches is equal to 7.25 inches.
Now, we can calculate how many pencils are measuring more than 5.5 inches but less than 7.25 inches. To do this, we will subtract the smaller number (5.5) from the larger number (7.25).
7.25 - 5.5 = 1.75
This means that there are 1.75 inches between the two measurements. Since each pencil takes up about 0.25 inches, we can divide 1.75 by 0.25 to determine how many pencils would fit in that space.
1.75 / 0.25 = 7
Therefore, there are 7 pencils measuring more than 5 1/2 inches but less than 7 2/4 inches.
To know more about inch click-
https://brainly.com/question/29813582
#SPJ1
Complete questions as follows-
how many pencils measure more than 5 1/2 inches but less than 7 2/4 inches?
5a. find the value of a.

Answers
The logarithmic function f(x) = a·log₃(x - 4), passing through the points (13, 7), has the values;
5 a. The value of a is 3.5
b. Please find attached the graph of the function, f(x) = 3.5·log₃(x - 4), created with MS Excel
What is a logarithmic function?A logarithmic function is a function that contain and involves logarithm operation and it is the inverse of an exponential function
The function is f(x) = a·log₃(x - 4),
x > 4 and a > 0
The coordinates of a point on the graph of the function, f is A(13, 7)
5 a. The value of a can be found by plugging in the value of (13, 7) = (x, f(x)), as follows
f(13) = 7 = a·log₃(13 - 4) = a·log₃9 = a·log₃3²
7 = a·log₃3²
7 = 2·a·log₃3 = 2·a·1 = 2·a
2·a = 7
a = 7 ÷ 2 = 3.5
a = 3.5
5 b. The coordinates of the x-intercept of the graph = (5, 0)
The equation of the function is;
f(x) = 3.5·log₃(x - 4)
A third point on the graph is given when f(x) = 14 as follows;
f(x) = 14 = 3.5·log₃(x - 4)
log₃(x - 4) = 14 ÷ 3.5 = 4
3⁴ = x - 4
x = 3⁴ + 4 = 85
Which gives the point, (85, 14)
Similarly, we have the point (31, 10.5), (7, 3.5)
Please find attached the graph of f(x) created with MS Excel
Learn more about logarithmic functions here:
https://brainly.com/question/28033379
#SPJ1

Which inequality is represented by the graph?


Answers
The inequality on the graph is the third option:
(2/5)*x - 3/2 ≥ y
Which inequality is represented by the graph?Let's analyse the graph if the inequality.
We can see that there is a solid linear equation with a positive slope, and the shaded area is below that line, then the inequality is of the form:
y ≤ linear equation.
We know that the symbol "≤" must be used because of the solid line.
We also can see that when x = 0, y takes a velue between -1 and -2.
With that in mind the correct option is the third one:
(4/5)*x - 2y ≥ 3
Isolating y we get:
(4/5)*x - 3 ≥ 2y
(2/5)*x - 3/2 ≥ y
Changing the order:
y ≤ (2/5)*x - 3/2
That is the graphed inequality.
Learn more about inequalities:
https://brainly.com/question/24372553
#SPJ1
what's the answer! Consider having a personal loan that spans 5 years. The loan was only taken out for $6000, but the interest rate was a higher fixed percentage of 5.99%. How much interest will you have paid after it is paid off?
Answers
Answer: $179.70
Step-by-step explanation:
The simple interest will be:
= (Principal × Rate × Time) / 100
= ($6000 × 5.99% × 5) / 10
= ($6000 × 0.0599 × 5) / 10
= $1797 / 10
= $179.70
Therefore, the total interest on the loan is $179.70
Please help me! Thanks
A farmer grows 360 pounds of apples. he sells them to a local grocer who divides them into 5 pound and 3 pound bags. If the grocer uses the same number of 5 pound bags as 3 pounds bags. How many bags did he use in all?
Answers
Answer:
96
Step-by-step explanation:
First divide 360 by 2.
Then divide 180 by 5 and that is how many 5 pound bags he will use.
Then divide 180 again by 3 and that is how many 3 pound bags he will use.
Find the distance from A to C across the gorge illustrated in the figure.

Answers
Answer:
\(\huge\boxed{\sf Opposite = 125.86 \ ft}\)
Step-by-step explanation:
This question will be solved using trigonometric ratios.
Given that,Angle = θ = 40°
Adjacent = 150 ft
To find:Opposite = ?
Using trigonometric ratio, tan θ.
Solution:\(\displaystyle tan \theta = \frac{opposite}{adjacent} \\\\Put \ the \ given.\\\\tan \ 40 = \frac{opposite}{150} \\\\0.839 = \frac{opposite}{150} \\\\Multiply \ both \ sides\ by \ 150\\\\0.839 \times 150 = opposite\\\\125.86 \ ft = Opposite\\\\Opposite = 125.86 \ ft\\\\\rule[225]{225}{2}\)
PLEASE HELP ASAP
solve -1/6[3-15(1/3)2]
![PLEASE HELP ASAP solve -1/6[3-15(1/3)2]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/C0Nx4ldjSdyeTD1pu34mYu8d7IAOliwi.png)
Answers
Answer:
C) -2/9
Step-by-step explanation:
\(\displaystyle -\frac{1}{6}\biggr[3-15\biggr(\frac{1}{3}\biggr)^2\biggr]\\\\=-\frac{1}{6}\biggr[3-15\biggr(\frac{1}{9}\biggr)\biggr]\\\\=-\frac{1}{6}\biggr[3-\frac{15}{9}\biggr]\\\\=-\frac{1}{6}\biggr[\frac{27}{9}-\frac{15}{9}\biggr]\\\\=-\frac{1}{6}\biggr[\frac{12}{9}\biggr]\\\\=-\frac{1}{6}\biggr[\frac{4}{3}\biggr]\\\\=-\frac{4}{18}\\\\=-\frac{2}{9}\)
Answer:
Hence, Option (C) - 2/9 is the Answer:
Step-by-step explanation:
-1/6 [3 -15(1/3)^2]
-1/6(3 -15)(1/9))
-1/6(3 - 5/3)
-1/6 (4/3)
Hence, Option (C) - 2/9 is the Answer:
I hope it helps!
During the exponential phase, e.coli bacteria in a culture increase in number at a rate proportional to the current population. If growth rate is 1.9% per minute and the current population is 172.0 million, what will the population be 7.2 minutes from now?
Answers
During the exponential phase, e.coli bacteria in a culture increase in number at a rate proportional to the current population. If growth rate is 1.9% per minute and the current population is 172.0 million, the population 7.2 minutes from now can be calculated using the following formula:
P(t) = P ₀e^(rt)where ,P₀ = initial population r = growth rate (as a decimal) andt = time (in minutes)Substituting the given values, P₀ = 172.0 million r = 1.9% per minute = 0.019 per minute (as a decimal)t = 7.2 minutes
The population after 7.2 minutes will be:P(7.2) = 172.0 million * e^(0.019*7.2)≈ 234.0 million (rounded to the nearest tenth)Therefore, the population of e.coli bacteria 7.2 minutes from now will be approximately 234.0 million.
For more such questions on population
https://brainly.com/question/29885712
#SPJ8
Show that the equation 2sinxtanx+3=0 can be expressed as 2cos^(2)x-3cosx-2=0
Answers
The equation 2sin(x)tan(x) + 3 = 0 has been proved to equal 2cos²(x) - 3cos(x) - 2 = 0
How to prove the equationsFrom the question, we have the following equation that can be used in our computation:
2sinxtanx+3=0
Rewrite as
2sin(x)tan(x) + 3 = 0
Express tan(x) as tan(x) = sin(x)/cos(x)
So, we have
2sin²(x)/cos(x) + 3 = 0
Multiply through by cos(x)
2sin²(x) + 3cos(x) = 0
Express sin²(x) as 1 - cos²(x)
So, we have
2(1 - cos²(x)) + 3cos(x) = 0
Expand
2 - 2cos²(x) + 3cos(x) = 0
Multiply through by -1
-2 + 2cos²(x) - 3cos(x) = 0
Rearrange the terms
2cos²(x) - 3cos(x) - 2 = 0
Hence, the equation has been proved
Read more about trigonometry equations at
https://brainly.com/question/24349828
#SPJ1
What is 22 + 125 - 6
Answers
Answer:
141
Step-by-step explanation:
calculator
Answer:
141
Step-by-step explanation:
22+125=147
147-6=141
therefore
the answer is 141
NO LINKS!! Help me with the 2-Column Proof Part 5aa

Answers
Perpendicular lines intersect at 90° - definition of perpendicular.
Here is the two column proof:
Statement Reason
FH ⊥ NS Givenm∠FHS = 90° Definition of perpendicular lines∠FHS is a right angle Definition of a right angle ProvedFind the measure of ∠GJK. (I need the answer as fast as possible)

Answers
Answer:
∠ GJK = 102°
Step-by-step explanation:
(2x + 92) and (3x + 63) are same- side interior angles and sum to 180° , so
2x + 92 + 3x + 63 = 180
5x + 155 = 180 ( subtract 155 from both sides )
5x = 25 ( divide both sides by 5 )
x = 5
Then
∠ GJK = 2x + 92 = 2(5) + 92 = 10 + 92 = 102°
Runners at a cross-country meet run 2 miles south and then 4 miles west from the starting line. Determine the shortest straight path they must run to get back to the starting line. Brainliest and 20 points

Answers
Answer:
√20 miles
Step-by-step explanation:
a² + b² = c²
|
? | 2 miles ↓
|
------------------------------
← 4 miles
2² + 4² = c²
4 + 16 = c²
20 = c²
√20 = c
I hope this helps!
The length of the straight path they must run to get back to the starting line is 4.47 miles.
What is displacement?Displacement [x] of an object is the length of the straight line joining the initial and final position of the object. Mathematically, displacement can be written as-
Δx = x[2] - x[1]
Now -
Δx = vΔt {[v] is velocity}
So we can write -
vΔt = x[2] - x[1]
Given are the runners at a cross-country meet such that they ran 2 miles to south and then 4 miles to west from the starting line.
We can find the straight path they must run to get back to the starting line using the Pythagoras theorem. The base will be equal to distance ran towards south and height will be equal to the distance ran towards west. The length of the hypotenuse will be equal to that of displacement or the straight path they must run to get back to the starting line. Using Pythagoras theorem -
[h]² = [b]² + [p]²
[h]² = (2 x 2) + (4 x 4)
[h]² = 4 + 16
[h]² = 20
[h] = 4.47 miles
Therefore, the length of the straight path they must run to get back to the starting line is 4.47 miles.
To solve more questions on Kinematics, visit the link below-
brainly.com/question/17465675
#SPJ5
