Decrypt these messages that were encrypted using the Caesar cipher. a) EOXH MHDQV b) WHVW WRGDB c) HDW GLP VXP
Answers
The decrypted messages using Caesar cipher are: a) EOXH MHDQV - BLUE JACKET b) WHVW WRGDB -TESTING ONE c) HDW GLP VXP - CAT AND DOG
The Caesar cipher is a simple substitution cipher that replaces each letter in the plaintext by a letter a fixed number of positions down the alphabet. To decrypt messages that were encrypted using the Caesar cipher, we need to shift the letters in the opposite direction.
For message a), we need to shift the letters 3 positions to the left. So, E becomes B, O becomes L, X becomes U, and so on. Thus, the decrypted message is "BLUE JACKET".
For message b), we need to shift the letters 3 positions to the right. So, W becomes Z, H becomes K, V becomes Y, and so on. Thus, the decrypted message is "TESTING ONE".
For message c), we need to shift the letters 7 positions to the left. So, H becomes A, D becomes W, W becomes P, and so on. Thus, the decrypted message is "CAT AND DOG".
In summary, to decrypt messages encrypted using the Caesar cipher, we need to shift the letters in the opposite direction by the same number of positions. It is a simple technique that can be easily cracked with modern encryption algorithms, but it is still useful for educational purposes and for encrypting simple messages.
For more such questions on Caesar cipher.
https://brainly.com/question/14754515#
#SPJ11
Related Questions
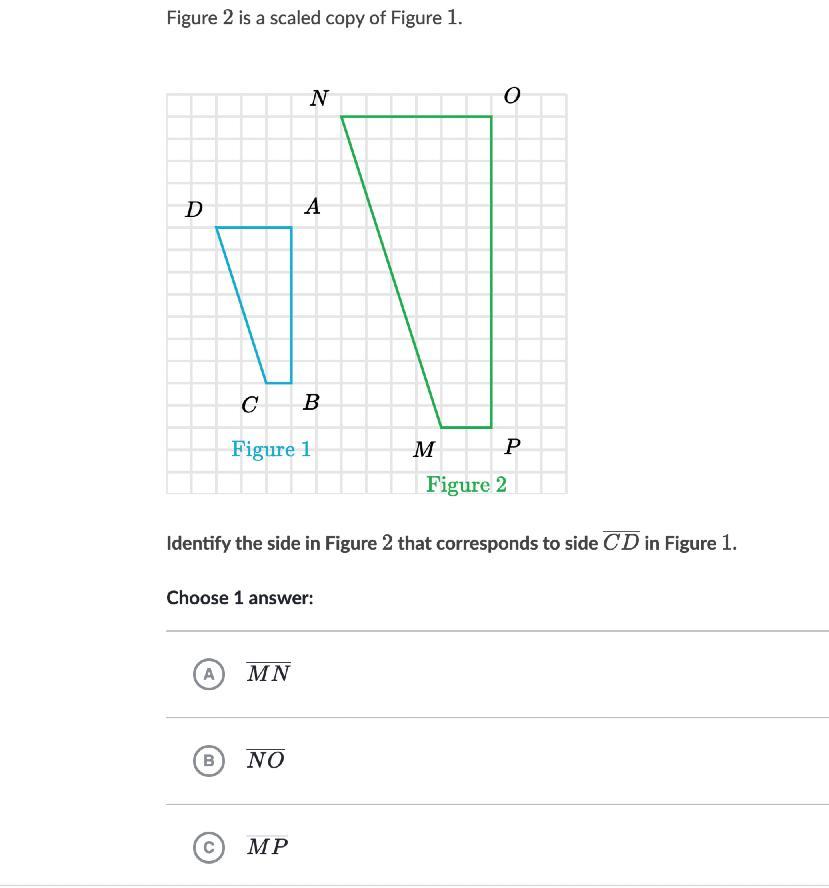
Figure 222 is a scaled copy of Figure 111.
PLEASE HELP
Identify the side in Figure 222 that corresponds to side \overline{CD}
CD
start overline, C, D, end overline in Figure 111.
Choose 1 answer:
Choose 1 answer:
Answers
A 17.0-m-high and 11.0-m-long wall and its bracing under construction are shown in the figure. 17.0m 8.5 m 10 braces Calculate the force, in newtons, exerted by each of the 10 braces if a strong wind exerts a horizontal force of 645 N on each square meter of the wall. Assume that the net force from the wind acts at a height halfway up the wall and that all braces exert equal forces parallel to their lengths. Neglect the thickness of the wall. Grade Summary sin o cos tan o a tan a cotan sin h cos h tan h cotan h Degrees O Radians V
Answers
Therefore, each of the 10 braces exerts a force of approximately 6035.25 N.
To calculate the force exerted by each of the 10 braces, we need to consider the horizontal force exerted by the wind and the geometry of the wall and bracing.
Given:
Height of the wall (h) = 17.0 m
Length of the wall (l) = 11.0 m
Number of braces (n) = 10
Horizontal force exerted by the wind (F_w) = 645 N/m^2
First, let's calculate the total area of the wall:
Wall area (A) = h * l = 17.0 m * 11.0 m = 187.0 m^2
Since the net force from the wind acts at a height halfway up the wall, we can consider the force acting on the top half of the wall:
Force on the top half of the wall (F_t) = F_w * (A/2) = 645 N/m^2 * (187.0 m^2 / 2) = 60352.5 N
Next, let's calculate the force exerted by each brace:
Force exerted by each brace (F_brace) = F_t / n = 60352.5 N / 10 = 6035.25 N
Learn more about approximately here:
https://brainly.com/question/31695967
#SPJ11
Consider the following vector function. r(t) = 6t, 1 2 t2, t2 (a) Find the unit tangent and unit normal vectors T(t) and N(t). T(t) = N(t) = (b) Use this formula to find the curvature. κ(t) =
Answers
Using the formula the curvature. κ(t) = \(\frac{\sqrt{900t^2+6480}}{(5t^2+36)^2}\).
The reciprocal of a curve's radius can be used to compute an object's curvature. It is significant to keep in mind that the curvature varies depending on the kind of curve being evaluated.
From the question vector function
r(t) = <6t, t²/2, t²>
Now we have
r'(t) = (6, t, 2t)
and |r'(t)| = √(6)² + (t)² + (2t)²
|r'(t)| = √36 + t² + 4t²
|r'(t)| = √36 + 5t²
Now the unit tangent T(t) is given as:
T(t) = r'(t)/|r'(t)|
T(t) = (6, t, 2t)/√36 + 5t²
Now T'(t) = \(\left < \frac{-30t}{(36+5t^2)^{1/2}}, \frac{36}{(36+5t^2)^{1/2}},\frac{72}{(36+5t^2)^{1/2}}\right >\)
|T'(t)| = \(\sqrt{\frac{900t^2+6480}{(36+5t^2)^{3}}}\)
Therefore the unit normal N(t) is given by;
N(t) = T'(t)/|T'(t)
N(t) = \(\left < \frac{-30t}{\sqrt{900t^2+6480}}, \frac{36}{\sqrt{900t^2+6480}},\frac{72}{\sqrt{900t^2+6480}}\right >\)
Hence,
κ(t) = |T'(t)|/|r'(t)|
κ(t) = \(\frac{\sqrt{900t^2+6480}}{(5t^2+36)^2}\)
To learn kore about find the curvature link is here
brainly.com/question/12982907
#SPJ4
For Each Function Find An Equation For F−1(X), The Inverse Function. A. F(X)=X4+9 B. F(X)=(X−1)3 C. F(X)=X+12x−3
Answers
For F(X) = X + 12X^(-3), the inverse function does not have a simple equation F^(-1)(X).
Let's find the inverse functions for each given function.
A. For F(X) = X^4 + 9:
To find the inverse function, we'll replace F(X) with Y:
Y = X^4 + 9
Now, let's swap X and Y and solve for Y to find the inverse function:
X = Y^4 + 9
Next, let's solve for Y:
Y^4 = X - 9
Y = (X - 9)^(1/4)
Therefore, the inverse function for F(X) = X^4 + 9 is F^(-1)(X) = (X - 9)^(1/4).
B. For F(X) = (X - 1)^3:
Following the same steps as above, we'll replace F(X) with Y:
Y = (X - 1)^3
Swap X and Y and solve for Y:
X = (Y - 1)^3
Solve for Y:
(Y - 1)^3 = X
Y - 1 = X^(1/3)
Y = X^(1/3) + 1
Therefore, the inverse function for F(X) = (X - 1)^3 is F^(-1)(X) = X^(1/3) + 1.
C. For F(X) = X + 12X^(-3):
Replacing F(X) with Y:
Y = X + 12X^(-3)
Swap X and Y and solve for Y:
X = Y + 12Y^(-3)
Solve for Y:
Y + 12Y^(-3) = X
12Y^(-3) + Y = X
12 + Y^4 = XY
This equation is not easily solvable for Y as an explicit function of X. In this case, the inverse function cannot be expressed in a simple form.
Therefore, for F(X) = X + 12X^(-3), the inverse function does not have a simple equation F^(-1)(X).
Please note that for the cases where the inverse function does not have a simple equation, it may still exist and can be represented using other methods such as implicit equations or graphs.
Learn more about inverse function here
https://brainly.com/question/11735394
#SPJ11
evaluating reports , help me please ...

Answers
Please help.
Find the value of x

Answers
Answer:
The value of x is 18
Step-by-step explanation:
24 x 15 is 360. ( x + 12 ) x 12 = 360 as well. So, 360÷12=30. 30-12 = 18. So the full equation is (18+12)x12=24×15 which are both equal to 360.
A symmetric beam-splitter has two input modes and two output modes. Determne the output if the input state is ∣20⟩. Show your working carefully to get full marks. You may use some or all of the following information for the same symmetric peam-splitter: the different input state ∣10⟩ produces an output U^∣10⟩=21(∣10⟩+ i01⟩) where the unitary operator U^ has the property that U^a^1†U^†=21(a^1†+ia^2†).
Answers
A beam splitter is an optical device used to split an incident beam of light into two or more beams. A beam splitter with two input modes and two output modes is called a symmetric beam splitter.
When the input state is ∣20⟩, we must determine the output. We can use the given information to solve this problem.To solve this problem, we will use the following steps:
Step 1: Determine the unitary operator U for the symmetric beam splitter
We can use the information provided to determine the unitary operator U for the symmetric beam splitter.
The input state ∣10⟩ produces an output \(U^∣10⟩=21(∣10⟩+i∣01⟩)\) where U is the unitary operator.
We can rearrange this expression to get U^∣10⟩=21∣10⟩+i21∣01⟩.
Since the beam splitter is symmetric, it must be the case that U∣01⟩=21(∣10⟩+i∣01⟩).
We can use this expression to find U:
\(U^∣01⟩=21(∣10⟩+i∣01⟩)Ua^2†U^†=21(a^1†+ia^2†)U^∣01⟩=21(a^1†+ia^2†)\)
Since a^1†=∣10⟩ and a^2†=∣01⟩, we can substitute these expressions into the above equation to get:
U^∣01⟩=21(∣10⟩+i∣01⟩)U^|01> = 1/√2(|10⟩ + i|01⟩)
Step 2: Calculate the output for the input state ∣10⟩
Using the expression for U^ from step 1, we can calculate the output for the input state ∣10⟩.U^∣10⟩=21(∣10⟩+i∣01⟩)U^|10> = 1/√2(|10⟩ + i|01⟩)∣10⟩ is an eigenstate of the symmetric beam splitter, so the output for this input state is simply ∣10⟩.
Therefore, the output for ∣10⟩ is 1/√2(|10⟩ + i|01⟩)
Step 3: Use the output from step 2 to calculate the output for the input state ∣20⟩
We can use the superposition principle to calculate the output for the input state ∣20⟩.
Since ∣20⟩ = ∣10⟩ ⊗ ∣10⟩, we can write the input state as:
∣20⟩ = ∣10⟩ ⊗ ∣10⟩The output state for ∣20⟩ is given by:
U^∣20⟩=U^∣10⟩ ⊗ U^∣10⟩=1/2(|10⟩ + i|01⟩) ⊗ 1/2(|10⟩ + i|01⟩)=1/4(|10⟩⊗|10⟩ + i|10⟩⊗|01⟩+ i|01⟩⊗|10⟩ - |01⟩⊗|01⟩)Therefore, the output for ∣20⟩ is 1/4(|10⟩⊗|10⟩ + i|10⟩⊗|01⟩+ i|01⟩⊗|10⟩ - |01⟩⊗|01⟩).
Therefore, the output for the input state ∣20⟩ is 1/4(|10⟩⊗|10⟩ + i|10⟩⊗|01⟩+ i|01⟩⊗|10⟩ - |01⟩⊗|01⟩).
To know more about superposition principle visit:
brainly.com/question/30780170
#SPJ11
Simplify: (3x)⁰÷5‐²
Answers
Answer:
(3x)⁰÷5‐²
1 ÷5‐²
5²
25
Lin rode her bike 2 miles in 8 minutes. She rode at a constant speed. Complete the table to show the time it took her to travel different distances at this speed. How many miles can she travel in a minute?

Answers
Answer:
4 and 1/4, 1/4 miles or quarter mile in a minute
Step-by-step explanation:
2 x 4 =8
1 × 4 =4
1/4 x 4 =1
What is the optimal choice when pı = 3, P2 = 5 and I = 20 and utility is (a) u(x1, x2) = min{2x1, x2} (b) u(x^2 1, x^2 2) = x} + x3 (c) u(x1, x2) = In(xi) + In(x2) (d) u(x1, x2) = x x = (e) u(x1, x2) = -(x1 - 1)^2 – (x2 - 1)^2
Answers
Using the Lagrange method, the optimal choice is therefore (x1, x2) = (20/9, 4/3).
The optimal choice when pı = 3, P2 = 5 and I = 20 and utility is u(x1, x2) = min{2x1, x2} can be found using the Lagrange method .Lagrange method: This method involves formulating a function (the Lagrange function) which should be optimized with constraints, i.e. the optimal result should be produced while adhering to the constraints provided. The Lagrange function is given by: L(x1, x2, λ) = u(x1, x2) - λ(I - p1x1 - p2x2)
Where L is the Lagrange function, λ is the Lagrange multiplier, I is the budget, p1 is the price of good 1, p2 is the price of good 2.The optimal choice can be determined by the partial derivatives of L with respect to x1, x2, and λ, and setting them to zero to get the critical points. Then, the second partial derivative test is used to determine if the critical points are maxima, minima, or saddle points. The critical points of the Lagrange function L are:
∂L/∂x1 = 2λ - 2p1 = 0 ∂L/∂x2 = λ - p2 = 0 ∂L/∂λ = I - p1x1 - p2x2 = 0
Substitute the first equation into the second equation to get:λ = p2,2λ = 2p1 ⇒ p2 = 2p1,
Substitute the first two equations into the third equation to get: x1 = I/3p1,x2 = I/5p2
Substitute p2 = 2p1 into the above to get:x1 = I/3p1,x2 = I/10p1.Substitute the values of p1, p2 and I into the above to get:x1 = 20/9,x2 = 4/3.The optimal choice is therefore (x1, x2) = (20/9, 4/3).
More on Lagrange method: https://brainly.com/question/31133918
#SPJ11
To rent a certain meeting room, a college charges a reservation fee of $44 and an additional fee of $7.40 per hour. The history club wants to spend less than
$73.60 on renting the meeting room.
What are the possible amounts of time for which they could rent the meeting room?
Use t for the number of hours the meeting room is rented, and solve your Inequality for t.
Answers
Answer:
t<4
Step-by-step explanation:
mateo is playing a word game where he's trying to make 444-letter words by rearranging the letters in the word iron. how many unique ways are there to arrange the letters in the word iron?
Answers
The word IRON can be arranged is 24 unique ways.
Given:
The word = IRON
The number of unique ways in which the letters in the word IRON can be arranged = ?
The number of letters in IRON = 4
The number of positions = 4
In the first position, any one of the 4 letters can be placed
In the second position any one of the remaining 3 letters can be placed
In the third position any one of the remaining 2 letters can be placed
The fourth position can be filled with the left over letter
So the total number arrangement in unique way
= (Number of ways to fill in 1st position)* (Number of ways to fill in 2nd position)* (Number of ways to fill in 3rd position)* (Number of ways to fill in 4th position)
=> 4 *3*2*1
= 24 ways
Hence, The word IRON can be arranged is 24 unique ways.
To know more about letters check the below link:
https://brainly.com/question/28463311
#SPJ1
Find the slope of any line parallel to the line through (6, 2) and (-6, 3).Slope=

Answers
Parallel lines will have the same slope.
Then we can calculate the slope for this line and it will be the same for all its parallel lines.
Given two points (x1,y1) = (6,2) and (x2,y2) = (-6,3) we can calculate the slope m as:
\(m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-2}{-6-6}=\frac{1}{-12}=-\frac{1}{12}\)The slope for this line and all its parallels is m = -1/12.
Answer: -1/12
Solve for j.
-41j+ 14j-28j - 10 = 45
Answers
Answer:
j = -1
Step-by-step explanation:
add the 10 to right side
-41j + 14 j - 28j = 55
-41j+ 14j -28j = -55j
-55j = 55
j = -1
Select the domain and range of F.
F={(x, y) Ix+y=10].
1. Set F is not a function and does not contain a domain or range
2. Domain: [10] Range: (10)
3. Domain: All Real Numbers Range: All Real Numbers
Answers
The domain and range of F is F={(x, y) Ix+y=10] is: 3. Domain: All Real Numbers Range: All Real Numbers
The given set F={(x, y) | x+y=10} represents a linear equation where the sum of x and y is always equal to 10.
To determine the domain and range of F, we need to consider the
possible values of x and y that satisfy the equation.
Domain: The domain represents the set of all possible values for the independent variable, which in this case is x. Since there are no restrictions on the value of x, the domain is All Real Numbers.
Range: The range represents the set of all possible values for the dependent variable, which in this case is y. By rearranging the equation x+y=10, we can solve for y to get y=10-x. Since x can take any real value, y can also take any real value. Therefore, the range is also All Real Numbers.
The correct answer is: 3. Domain: All Real Numbers Range: All Real Numbers
For more such questions on domain
https://brainly.com/question/26098895
#SPJ8
i lost my old brainly account name it was called official norths :( i forgot the password i will love if you help me with this please The formula F=1.8C + 32 is used to convert temperatures between degrees Fahrenheit (F) and degrees Celsius (C). How many degrees Fahrenheit is it if it is currently 30º C?
Answers
Answer:
86° Fahrenheit
Step-by-step explanation:
F=1.8C + 32
C=30°
Plugging into the formula:
\(F=1.8*30+32\\F=54+32\\F=86\)
The Fahrenheit for 30° Celsius using the given formula is 86° Fahrenheit.
Answer:
86 degrees
Step-by-step explanation:
(2x² + 3x − 9)
Factor
Answers
D. Curved arrows and Resonance Identify whether the curved arrow notation in each of the following cases is correct or not If incorrect, Explain why.
Answers
To assess the correctness of the curved arrow notation in each case, specific examples or instances of the notation are needed. Without such examples, it is challenging to provide a meaningful analysis or explanation of whether the curved arrow notation is correct or incorrect.
Curved arrow notation is commonly used in organic chemistry to represent electron movement in chemical reactions and mechanisms. It indicates the flow of electrons, such as the movement of lone pairs, bonding electrons, or the formation/breakage of bonds. The notation is essential for understanding reaction mechanisms and the distribution of electron density in molecules.
To determine the correctness of curved arrow notation, one needs to evaluate whether it accurately represents the movement of electrons according to the established rules and principles of organic chemistry. This involves considering factors such as electron pair repulsion, formal charges, bond breaking/forming, and resonance structures.
Without specific examples or instances of the curved arrow notation in question, it is not possible to provide a comprehensive analysis or explanation. If you can provide specific examples or questions regarding the curved arrow notation, I would be glad to assist you further.
Learn more about determine here
brainly.com/question/29898039
#SPJ11
1. Let x ∈ Z. Prove that if 3 | 2x, then 3 | x.2. Let n ∈ Z. Prove that 3 | (2n 2 + 1) if and only if 3 - n.
Answers
Answer:
1.Suppose 3 | 2x. Then we can write 2x = 3k for some integer k. Rearranging, we have x = (3/2)k. Since k is an integer, (3/2)k is also an integer, which means that x is divisible by 3. Hence, 3 | x.
First, suppose 3 | (2n^2 + 1). Then we can write 2n^2 + 1 = 3k for some integer k. Rearranging, we have 2n^2 = 3k - 1. Since 3k - 1 is odd, we can write it as 2m + 1 for some integer m. Substituting, we have 2n^2 = 2m + 1, which implies that n^2 = m + (1/2). But since m is an integer, (1/2)m is not an integer, which means that n^2 is not an integer. This is a contradiction, so our assumption that 3 | (2n^2 + 1) must be false.
Now suppose 3 - n. Then we can write n = 3k - 1 for some integer k. Substituting, we have 2n^2 + 1 = 18k^2 - 12k + 3. Factoring out 3, we have 2n^2 + 1 = 3(6k^2 - 4k + 1). But 6k^2 - 4k + 1 is always an integer, so if 3 - n, then 3 | (2n^2 + 1).
give me thanks for more! your welcome!
Step-by-step explanation:
A sample of radium-226 has a mass of 100 mg. Find a formula for the mass of the sample that remains after t years. (b) Find the mass after 500 years correct to the nearest milligram. (c) When will the mass be reduced to 30 mg?
Answers
a) formula for the mass of the sample that remains after t years is k = -ln(1/2) / 1600
b) the mass after 500 years is \(100 * e^{(-(-ln(1/2) / 1600) * 500)\)
c) t = ln(30/100) / k will the mass be reduced to 30 mg.
What is sample?
In statistics, a sample refers to a subset of individuals, items, or elements selected from a larger population. It is a representative subset of the population that is used to gather information and draw inferences about the entire population.
a) The decay of radium-226 follows an exponential decay model, where the mass remaining after a certain time is given by the formula:
\(m(t) = m(0) * e^{(-kt)\)
where:
m(t) is the mass remaining after time t
m(0) is the initial mass
k is the decay constant
To find the decay constant, we can use the half-life of radium-226, which is approximately 1600 years. The half-life is the time it takes for half of the initial mass to decay.
Using the half-life formula:
\((1/2) = e^{(-k * 1600)\)
Taking the natural logarithm (ln) of both sides:
ln(1/2) = -k * 1600
Solving for k:
k = -ln(1/2) / 1600
Now, we can substitute the value of k into the formula to find the mass remaining after a given time.
b) After 500 years:
\(m(500) = 100 * e^{(-k * 500)\)
Substituting the value of k:
\(m(500) = 100 * e^{(-(-ln(1/2) / 1600) * 500)\)
Calculating the approximate value of m(500) to the nearest milligram will require a calculator or software. Let's denote the result as m_500.
c) To find when the mass is reduced to 30 mg, we can set up the equation:
\(30 = 100 * e^{(-k * t)\)
Solving for t:
\(e^{(-k * t)} = 30 / 100\\\\-e^{(-k * t)} = -ln(30/100)\)
k * t = ln(30/100)
t = ln(30/100) / k
Substituting the value of k and calculating the approximate value of t will give us the time it takes to reach a mass of 30 mg.
To learn more about sample visit:
https://brainly.com/question/24466382
#SPJ4
Please help asap :( Find the exact length of arc ADC. In your final answer, include all of your calculations
Answers
Answer:
15 Pi m
Step-by-step explanation:
arc ADC = 360 Degrees - 60 Degrees divided by 360 Degrees Multiplied by 2 Pi Multiplied by 9
= 5/6 Times 18 Pi
=15 Pi m
Seven times the sum of a number and 3 is 9.
Answers
Answer: -1.71
7(x+3) = 9 is the equation
7x+21 = 9
7x = -12
x= -12/7
x= -1.71
At what values of x does the graph of y=x^ 2 e^-2 have a point of inflection?
Answers
The graph of y = x^2e^(-2) has a point of inflection at the values of x where the concavity of the curve changes. In mathematical terms, a point of inflection occurs where the second derivative of the function changes sign.
To find the values of x that correspond to the points of inflection, we need to find the second derivative of the function and solve for the values of x that make the second derivative equal to zero or undefined.
First, let's find the first and second derivatives of y = x^2e^(-2):
First derivative:
dy/dx = 2xe^(-2) + x^2(-2)e^(-2) = 2xe^(-2) - 2x^2e^(-2)
Second derivative:
d^2y/dx^2 = 2e^(-2) - 4xe^(-2) = 2e^(-2)(1 - 2x)
Now, set the second derivative equal to zero and solve for x:
2e^(-2)(1 - 2x) = 0
Since e^(-2) is always positive and nonzero, we can ignore it for solving this equation. Therefore:
1 - 2x = 0
2x = 1
x = 1/2
So, the graph of y = x^2e^(-2) has a point of inflection at x = 1/2.
Learn more about points of inflection and curve concavity in calculus here:
https://brainly.com/question/29164810
#SPJ11
Find the sum of the following using the column method a^2+2*ab+b^2, a^2-2*ab-b^2, a^2+b^2
Answers
The sum of the given expressions using the column method is 3a^2.
The sum of the given expressions can be found using the column method. Let's break it down step-by-step:
1. First, let's consider the expression a^2 + 2ab + b^2.
2. Write down the expression vertically, with each term aligned under its respective power of a:
a^2
+ 2ab
+ b^2
3. Add the corresponding terms vertically:
(a^2 + 2ab + b^2)
4. Next, let's consider the expression a^2 - 2ab - b^2.
5. Write down the expression vertically, with each term aligned under its respective power of a:
a^2
- 2ab
- b^2
6. Add the corresponding terms vertically:
(a^2 - 2ab - b^2)
7. Finally, let's consider the expression a^2 + b^2.
8. Write down the expression vertically, with each term aligned under its respective power of a:
a^2
b^2
9. Add the corresponding terms vertically:
(a^2 + b^2)
10. Now, we can find the sum of all the expressions by adding the results from steps 3, 6, and 9:
(a^2 + 2ab + b^2) + (a^2 - 2ab - b^2) + (a^2 + b^2)
11. Simplify the expression:
a^2 + 2ab + b^2 + a^2 - 2ab - b^2 + a^2 + b^2
12. Combine like terms:
3a^2
Therefore, the sum of the given expressions using the column method is 3a^2.
Learn more about sum :
https://brainly.com/question/641910
#SPJ11
Jay is buying pumpkins at a pumpkin patch to decorate his front porch. The pumpkins are $3.50 each and he wants to spend less than $25. Write an inequality that represents how many pumpkins, p, Jay can buy.
Answers
Answer:
Step-by-step explanation:
Given that:
Let x represent the number of pumpkins that can be purchased for $25
The cost of a particular pumpkin to decorate a porch = $3.50
The amount to be spent on pumpkins by Jay is x < $25
Thus,
With such an amount;
Jay would be able to buy $25/$3.50 = 7 pumpkins
The average (mean) of five numbers is 30.
Four of the numbers are 21, 29, 18 and 32.
What is the fifth number?
Answers
Answer:
50
Step-by-step explanation:
x/5 = 30
= 30 x 5
= 150
150 - (21 + 29+ 18 + 32)= 50
the fifth number is 50.
The fifth number is 50 and this can be determined by using the formula of the mean and also by using the arithmetic operations.
Given :
The average (mean) of five numbers is 30. Four of the numbers are 21, 29, 18, and 32.Let the sum of five numbers be 'x'. Then the mean is given by the formula:
\(\rm Mean =\dfrac{Sum\;of\;all\;data}{Total \; number\;of\;data}\)
Now, substitute the known values in the above expression.
\(30=\dfrac{x}{5}\)
x = 30 \(\times\) 5
x = 150
So, the sum of five numbers is 150 that is:
21 + 29 + 18 + 32 + a = 150
where 'a' is the fifth number.
Simplify the above expression in order to find the fifth number.
100 + a = 150
a = 150 - 100
a = 50
So, the fifth number is 50.
For more information, refer to the link given below:
https://brainly.com/question/1957976
find parametric equations for the line tangent to the curve of intersection of the surfaces at the given point.
Answers
To find parametric equations for the line tangent to the curve of the intersection of the surfaces at the given point, you can follow the steps below
Step 1: Find the equation for the curve of the intersection of the surfaces to find the equation for the curve of intersection of the surfaces, we need to solve the given equations simultaneously
Equation 1: y = x^2Equation 2: z = x + substituting Equation 1 into Equation 2, we get:z = x + x^2
This is the equation for the curve of intersection of the surfaces.
Step 2: Differentiate the equation obtained in step 1 to get the slope of the tangent line at the given point
Differentiating the equation above with respect to x, we get dz/dx = 1 + 2xAt the given point (1,1,2), the slope of the tangent line is:dz/dx = 1 + 2(1) = 3
Step 3: Use the point and slope from step 2 to find the equation of the tangent line in point-slope formThe equation of the tangent line in point-slope form:y - 1 = 3(x - 1)
Step 4: Convert the point-slope form to parametric form if necessaryThe parametric equations of the tangent line are:x = t + 1y = 3t + 1z = 2t + 2Step 5: Write the main answer and conclusion according to the question givenMain answer: The parametric equations of the line tangent to the curve of intersection of the surfaces y = x^2 and z = x + y at the point (1,1,2) are:x = t + 1y = 3t + 1z = 2t + 2Conclusion: The parametric equations of the tangent line are x = t + 1, y = 3t + 1, z = 2t + 2.
for more visit brainly.com/question/29275326
#SPJ11
This site sucks it does help me at all
Answers
Answer:Then try using quizlit hope this helps u!
Step-by-step explanation:May i also get brainlist only if u wanna give me brainlist though! Good day sir ma'am
Answer:
We sorry that the site sucks!!
Step-by-step explanation:
The reason why it might suck is because people might troll with the answers or etc!
helpppp meee pleaseeee please

Answers
Answer:
58 units
Step-by-step explanation:
Isosceles triangle, so the top two sides are 19
19+19=38
The base is 11+9=20
38+20=58
Find the function of (0,6), (3,15.8) and (9.5,0)
Answers
The polynomic function that contains the points (0, 6), (3, 15.8) and (9.5, 0) is a quadratic function, whose model is y = -0.600 · x² + 5.066 · x + 6.
How to derive a polynomic function from given points
To determine the coefficients of a polynomic function we must know a set of distinct points, whose number is the same number of coefficients. In this case, we can derive a quadratic function, as quadratic functions have three coefficients:
y = a · x² + b · x + c (1)
Now we substitute x and y in (1) and solve the resulting system of linear equations:
c = 6
9 · a + 3 · b + c = 15.8
90.25 · a + 9.5 · b + c = 0
Whose solution is a ≈ -0.600, b ≈ 5.066 and c = 6.
Remark
The statement is incomplete. The complete form is shown below:
There is a polynomial function. Find the function of (0, 6), (3, 15.8) and (9.5, 0).
To learn more on polynomials: https://brainly.com/question/11536910
#SPJ1