Convert the following from standard for to vertex form.
f(x)=2x²+7X+5 ​

Answer:

• (a)80 mg

• (c)f(t)=80(0.5)^t

• (d)0.625 mg

Explanation:

Part A

From the point (0, 80), we see that the person took 80 mg of the medicine at the start.

Part B

From the graph:

From points (0,80) and (2,20); and (2,20) and (4,5)

• After 2 hours, the amount of medicine has been reduced by a factor of 1/4.

Therefore, after 1 hour, the amount of medicine is reduced by a factor of 1/2.

The completed table is attached below:

Part C

An exponential function is written in the form:

Since the amount of medicine is halved every 1 hour:

The rate of decrease = 1/2

The starting amount, Ao = 80 mg

Therefore, an equation that defines f is:

Part D

After 7 hours, when t=7

After 7 hours, 0.625 mg of medicine remains in the person's body.

To find the area of a composite figure, we need to break it down into simpler shapes and add up their areas and the area of the composite figure is 57 square units.

We must separate a composite figure into simpler shapes and sum up their areas in order to determine the area of the composite figure.

When we look at the image, we can see that it is composed of a triangle, two rectangles, and a circle.

The length times the breadth of the left rectangle equals 4 times the width of the rectangle, or 24 square units.

Half the sum of the triangle's base, height, and surface. The breadth of the left rectangle is the same as the base, which is 6 units, and the height is 3 units (the same as the height of the figure). As a result, the triangular has a surface area of 9 square units, or 1/2 times 6 times 3.

The length times the breadth of the right rectangle equals 6 times the width, or 24 square units, to determine its area.

The three forms' total areas add up to: 24 + 9 + 24 = 57

57 square units make up the area of this composite image.

Learn more about area here:

https://brainly.com/question/27683633

#SPJ1

There are 8.0658 × \(10^{67}\) more form to shuffle a deck of cards than atoms.

What is the factorial?

Factorial is an important function, which is used to find how many ways things can be arranged or the ordered set of numbers.The factorial of a whole number is the function that multiplies the number by  number below it.

The number of ways to shuffle a deck of cards is astronomically large, far greater than the estimated number of atoms in the observable universe.

A standard deck of 52 playing cards can be arranged in 52 factorial ways, denoted as 52!. This means multiplying all the positive integers from 1 to 52 together:

52! = 52 × 51 × 50 × ... × 3 × 2 × 1=8.0658 × \(10^{67}\).

Therefore,the exact value of 52! is an  large number, approximately equal to 8.0658×\(10^{67}\).

To learn more about the factorial refer here

brainly.com/question/25997932

#SPJ4



Answer:

14 miles per hour

Step-by-step explanation:

60/15=4

3.5*4= 14

14miles per 60mintues (1 hour)

answer:the answer for digital index of 23475 is 3

answer: 3

explanation: the digital index is 3 because 23475 is divisible by 3

In anova, by dividing the mean square between groups by the mean square within groups, a(n) Analysis of variance  statistic is computed.

What is Analysis of variance ?

What are some instances where ANOVA has been applied?

Learn more about Analysis of variance

brainly.com/question/28274784

#SPJ4

The given information is as follows:A random sample of 150 teachers in an​ inner-city school district found that​ 72% of them had volunteered time to a local charitable cause within the past 12 months.

The formula for calculating the standard error of sample proportion is given as:$$Standard\(\ error=\frac{\sqrt{pq}}{n}$$\)where:p = proportion of success in the sampleq = proportion of failure in the samplen = sample sizeGiven:Sample proportion, p = 72% or 0.72Sample size, n = 150

The proportion of failure in the sample can be calculated as:q = 1 - p= 1 - 0.72= 0.28Substituting the known values in the above formula, we get:\($$Standard \ error=\frac{\sqrt{pq}}{n}$$$$=\frac{\sqrt{0.72(0.28)}}{150}$$$$=0.0372$$\)Rounding off to the nearest thousandth, we get the standard error of sample proportion as 0.037

To know more about values visit:

https://brainly.com/question/30145972

#SPJ11

\(~~~~~~ \textit{Simple Interest Earned} \\\\ I = Prt\qquad \begin{cases} I=\textit{interest earned}\\ P=\textit{original amount deposited}\dotfill & \pounds 4000\\ r=rate\to 2.5\%\to \frac{2.5}{100}\dotfill &0.025\\ t=years\dotfill &4 \end{cases} \\\\\\ I = (4000)(0.025)(4)\implies I=400\)

False. A vertical line drawn through a normal distribution at z = 1.25 will not separate the distribution into two sections with a proportion of 0.1056 in the smaller section.

In a normal distribution, the area under the curve represents probabilities, and the total area under the curve is equal to 1. The proportion in any specific section of the distribution is represented by the area under the curve within that section. However, the exact proportion will depend on the specific value of z and the distribution's parameters.

When looking up a proportion in a standard normal distribution table, the table typically provides the area to the left of a given z-score. In this case, if we look up a z-score of 1.25 in the table, we find that the proportion to the left of z = 1.25 is approximately 0.8944. Therefore, the proportion in the smaller section (to the left of z = 1.25) would be 0.8944, not 0.1056. The proportion in the larger section (to the right of z = 1.25) would be 1 - 0.8944 = 0.1056.

Learn more about distribution here:

https://brainly.com/question/29664127

#SPJ11

\(10~~ : ~~45\implies \cfrac{10}{45}\implies \cfrac{5\cdot 2}{5\cdot 9}\implies \cfrac{5}{5}\cdot \cfrac{2}{9}\implies \cfrac{2}{9}\implies 2~~ : ~~9\)

Two of the diagonal elements being zero will result in the determinant being zero.

For square matrices of size n, with zeros anywhere possible off the diagonal and along their diagonal, we call these diagonal matrices.

(a) For the 2-by-2 case, the determinant of a 2-by-2 diagonal matrix is given by:

det(A) = a11 a22

If a11 or a22 is zero, then the determinant is zero. Therefore, if one of the diagonal elements is zero, the determinant will be zero.

(b) For the 3-by-3 case, the determinant of a 3-by-3 diagonal matrix is given by:

det(A) = a11 a22 a33

If a11, a22, or a33 is zero, then the determinant is zero. Therefore, if one of the diagonal elements is zero, the determinant will be zero.

(c) For the 4-by-4 case, the determinant of a 4-by-4 diagonal matrix is given by:

det(A) = a11 a22 a33 a44

If a11, a22, a33, or a44 is zero, then the determinant is zero. Therefore, if one of the diagonal elements is zero, the determinant will be zero.

If a22 and a33 are both zero, then the determinant of the 4-by-4 matrix is given by:

det(A) = a11 * 0 * 0 * a44 = 0

Therefore, two of the diagonal elements being zero will result in the determinant being zero.

In general, for an n-by-n diagonal matrix, if k diagonal elements are zero, then the determinant is zero if k > n-1, and non-zero if k ≤ n-1.

Learn more about matrix at: brainly.com/question/31409800

#SPJ11

Answer:

D

Step-by-step explanation:

Solving the inequality

- 3x + 5 > 4 ( subtract 5 from both sides )

- 3x > - 1

Divide both sides by - 3, reversing the symbol as a result of dividing by a negative value.

x < \(\frac{1}{3}\)

The only value not less than \(\frac{1}{3}\) is 4 → D

Polynomials are algebraic expressions consisting of terms that include real numbers, variables, and positive integer exponents. Each term in a polynomial has a variable raised to a non-negative integer power, and the coefficient of each term is a real number. Polynomials are classified by the degree of their highest power. If two or more terms in a polynomial have the same variable raised to the same power, they can be combined into a single term.

1. -x² + x - x² + 1

Combine like terms: -x² + x - x² + 1 = -2x² + x + 1

This polynomial has degree 2 because the highest power of the variable is 2.

2. x² + x + 2x³ - x

Rearrange terms: 2x³ + x² + x - x = 2x³ + x²

This polynomial has degree 3 because the highest power of the variable is 3.

3. 4x + x + x - 2

Combine like terms: 4x + x + x - 2 = 6x - 2

This polynomial has degree 1 because the highest power of the variable is 1.

4. 3x² + 4 - 3x² - 1

Combine like terms: 3x² - 3x² + 4 - 1 = 3

This polynomial has degree 0 because there is no variable term.

Therefore, the four given polynomials have degrees 2, 3, 1, and 0, respectively.

For such more question on variable

https://brainly.com/question/28248724

#SPJ8

According to the information provided, Jose's medically ideal weight is 250 pounds. Therefore, he would be considered to be obese when and if he weighed 300 pounds or more.

This means that the correct answer to the question is option b) 300.

It is important to note that obesity is typically defined as having a body mass index (BMI) of 30 or higher. BMI is calculated by dividing a person's weight in kilograms by their height in meters squared. A person's medically ideal weight is the weight that is considered healthy for their height and age.

BMI = (weight)/(maters squared)²

So, in summary, Jose would be considered to be obese when and if he weighed 300 pounds or more, as this would likely result in a BMI of 30 or higher, indicating obesity.

More information abaut BIM here: https://brainly.com/question/15894257

#SPJ11

The probability that an arriving student will find at least one other student waiting in line is approximately 0.167.

To solve this problem, we'll use the M/M/1 queueing model with Poisson arrivals and exponential service times. Let's calculate the required values: (a) Percentage of time Judy is idle: The utilization of the system (ρ) is the ratio of the average service time to the average interarrival time. In this case, the average service time is 10 minutes, and the average interarrival time is 12 minutes. Utilization (ρ) = Average service time / Average interarrival time = 10 / 12 = 5/6 ≈ 0.8333

The percentage of time Judy is idle is given by (1 - ρ) multiplied by 100: Idle percentage = (1 - 0.8333) * 100 ≈ 16.67%. Therefore, Judy is idle approximately 16.67% of the time. (b) Average waiting time for a student:

The average waiting time in a queue (Wq) can be calculated using Little's Law: Wq = Lq / λ, where Lq is the average number of customers in the queue and λ is the arrival rate. In this case, λ (arrival rate) = 1 customer per 12 minutes, and Lq can be calculated using the queuing formula: Lq = ρ^2 / (1 - ρ). Plugging in the values: Lq = (5/6)^2 / (1 - 5/6) = 25/6 ≈ 4.17 customers Wq = Lq / λ = 4.17 / (1/12) = 50 minutes. Therefore, on average, a student spends approximately 50 minutes waiting in line.

(c) Average length of the line: The average number of customers in the system (L) can be calculated using Little's Law: L = λ * W, where W is the average time a customer spends in the system. In this case, λ (arrival rate) = 1 customer per 12 minutes, and W can be calculated as W = Wq + 1/μ, where μ is the service rate (1/10 customers per minute). Plugging in the values: W = 50 + 1/ (1/10) = 50 + 10 = 60 minutes. L = λ * W = (1/12) * 60 = 5 customers. Therefore, on average, the line consists of approximately 5 customers.

(d) Probability of finding at least one student waiting in line: The probability that an arriving student finds at least one other student waiting in line is equal to the probability that the system is not empty. The probability that the system is not empty (P0) can be calculated using the formula: P0 = 1 - ρ, where ρ is the utilization. Plugging in the values:

P0 = 1 - 0.8333 ≈ 0.1667. Therefore, the probability that an arriving student will find at least one other student waiting in line is approximately 0.167.

To learn more about Probability, click here: brainly.com/question/16988487

#SPJ11

Answer:

The answer is 9

Step-by-step explanation:

1=x²-6x

(b/2)²=(-6/2)²=(3)²=9

Answer:

Step-by-step explanation:

Number of post-it notes can fit on the board:

Answer: 5.3

Step-by-step explanation:

\(-16t^2 +126t=217\\ \\ 16t^2 -126t+217=0\\\\t=\frac{-(-126) \pm \sqrt{(-126)^2 -4(16)(217)}}{2(16)}\\\\t \approx 5.3 \text{ } (t > 0)\)

The approximate range is -30 to 30. Therefore, the correct answer is option D.

The correlation coefficient r measures the strength and direction of a linear relationship between two variables, x and y. The correlation coefficient can range from -1 (perfectly negatively correlated, meaning as one variable increases, the other decreases) to 1 (perfectly positively correlated, meaning as one variable increases, the other increases).

When r = -0.9, this tells us that there is a strong negative linear relationship between x and y.

The equation for a linear relationship with a correlation coefficient of -0.9 is y = -0.9x + b, where b is the y-intercept. When x = 40, plugging this into the equation gives us y = -36.

So at an x-axis value of 40, the approximate range (lowest to highest) of y-values is -36 to 36. Since 36 is further away from the y-intercept than -36, the lowest possible value of y will be -30.

So, the approximate range is -30 to 30.

Therefore, the correct answer is option D.

Learn more about the correlation coefficient here:

https://brainly.com/question/27226153

#SPJ12

If the provided SHA hash value is different from the one I calculated, it indicates that there has been a modification or alteration in the data or the process used to calculate the hash.

This inconsistency raises concerns about data integrity and the authenticity of the information.

SHA (Secure Hash Algorithm) is a cryptographic hash function that generates a unique hash value for a given input. It is designed to be highly sensitive to any changes in the input data, meaning even a small alteration in the data will result in a completely different hash value. Therefore, if the provided SHA hash value differs from the one I calculated, it suggests that either the input data has been tampered with, or there is an error in the hash calculation process.

In such a situation, it is important to investigate the cause of the discrepancy and determine the source of the error. It could be due to accidental data corruption, intentional tampering, or an error in the hash calculation algorithm or implementation. Validating the integrity of the data becomes crucial to ensure the accuracy and trustworthiness of the information.

To resolve the issue, a comparison of the original and modified data should be conducted, and the hash calculation process should be carefully reviewed. It is also advisable to verify the integrity of the data through other means, such as using digital signatures or checksums, to detect any unauthorized modifications.

To know more about SHA (Secure Hash Algorithm) refer here:

https://brainly.com/question/13073367

#SPJ11

Answer:

47°

Step-by-step explanation:

if it is the same, then the angles are the same

180 - 85 - 48 = 47

a. The probability of success (hitting the target) is constant for each trial (88% or 0.88).

b. The probability of hitting the 6th target is:

P(X = 1) = C(1, 1) * 0.88^1 * (1 - 0.88)^(1 - 1) = 0.88

c. Using the binomial probability formula as before, with p = 0.88 and n = 3:

P(X = 1) = C(3, 1) * 0.88^1 * (1 - 0.88)^(3 - 1)

P(X = 2) = C(3, 2) * 0.88^2 * (1 - 0.88)^(3 - 2)

P(X = 3) = C(3, 3) * 0.88^3 * (1 - 0.88)^(3 - 3)

a) The three characteristics of this scenario that indicate we are working with Bernoulli trials are:

The experiment consists of a fixed number of trials (eight shots).

Each trial (shot) has two possible outcomes: hitting the target or missing the target.

The probability of success (hitting the target) is constant for each trial (88% or 0.88).

b) To find the probability of hitting the 6th target (considered as a single trial), we can use the binomial probability formula:

P(X = k) = C(n, k) * p^k * (1 - p)^(n - k)

where:

P(X = k) is the probability of getting exactly k successes,

C(n, k) is the binomial coefficient or number of ways to choose k successes out of n trials,

p is the probability of success in a single trial, and

n is the total number of trials.

In this case, k = 1 (hitting the target once), p = 0.88, and n = 1. Therefore, the probability of hitting the 6th target is:

P(X = 1) = C(1, 1) * 0.88^1 * (1 - 0.88)^(1 - 1) = 0.88

c) To find the probability that the first time hitting the target is not until the 4th shot, we need to consider the complementary event. The complementary event is hitting the target before the 4th shot.

P(not hitting until the 4th shot) = P(hitting on the 4th shot or later) = 1 - P(hitting on or before the 3rd shot)

The probability of hitting on or before the 3rd shot is the sum of the probabilities of hitting on the 1st, 2nd, and 3rd shots:

P(hitting on or before the 3rd shot) = P(X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3)

Using the binomial probability formula as before, with p = 0.88 and n = 3:

P(X = 1) = C(3, 1) * 0.88^1 * (1 - 0.88)^(3 - 1)

P(X = 2) = C(3, 2) * 0.88^2 * (1 - 0.88)^(3 - 2)

P(X = 3) = C(3, 3) * 0.88^3 * (1 - 0.88)^(3 - 3)

Calculate these probabilities and sum them up to find P(hitting on or before the 3rd shot), and then subtract from 1 to find the desired probability.

Learn more about  probability  from

https://brainly.com/question/30390037

#SPJ11

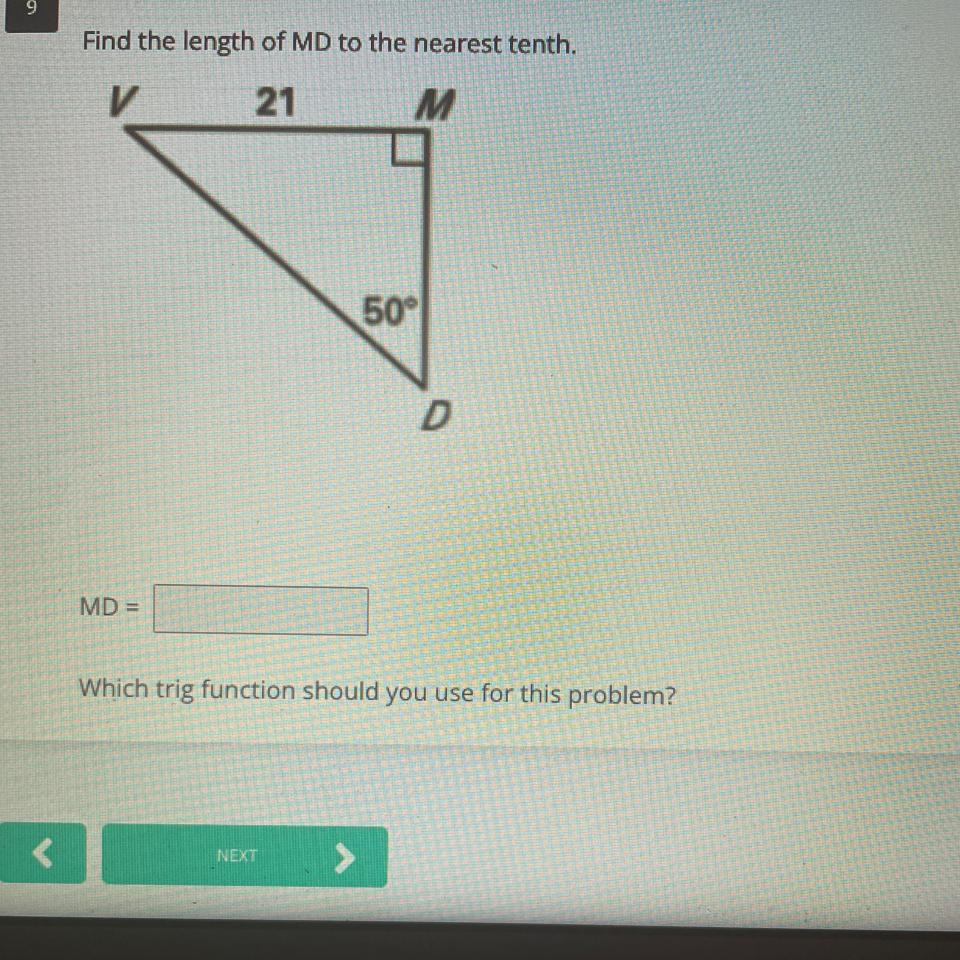
Answer:

Step-by-step explanation:

\(tan \ 50 =\dfrac{opposite \ side}{adjacent side}\\\\\\1.19=\dfrac{21}{MD}\\\\\\1.19*MD=21\\\\MD = \dfrac{21}{1.19}\\\\\\MD = 17.65\)

The elements of Z3[x]/(x^2 - x) are of the form ax + b that is multiplication table, where a and b are elements of Z3.

The multiplication table is:

  | 0   1   x   1+x   2   2+x

-------------------------------

0 | 0   0   0    0   0   0

1 | 0   1   x   1+x  2  2+x

x | 0   x  2x  2+x   x  1+2x

1+x| 0  1+x 2+x   2  2+x  x

2 | 0   2   x   2+x  1  1+x

2+x| 0  2+x 1+2x  x  1+x 2

Note that in this table, we use the fact that x^2 - x = 0, which implies that x^2 = x.

To know more about multiplication table,

https://brainly.com/question/30762398

#SPJ11

Two samples drawn from two populations are independent if the selection of one sample from a population is not related to the selection of the second sample from the same population. Option C is correct:

Independence is a fundamental concept in statistics when working with samples from different populations. It refers to the absence of any relationship or connection between the two samples. Option C correctly states that the selection of one sample from a population is not related to the selection of a second sample from the same population.

If the selection of one sample were related to the selection of the second sample from the same population (Option A), it would introduce bias and invalidate the assumption of independence. Similarly, if the two samples selected from the same population had a relationship or connection (Option B), it would violate the principle of independence.

Option D, stating that the selection of one sample from one population does not affect the selection of the second sample from the second population, is not the correct definition of independence. Independence refers to the relationship between samples drawn from the same population, rather than between samples drawn from different populations.

In summary, the independence of two samples implies that the selection of one sample from a population does not affect the selection of the second sample from the same population (Option C). This concept is crucial in statistical analysis to ensure unbiased and reliable results when working with multiple samples.

Learn more about samples here:

https://brainly.com/question/32907665

#SPJ11

A line is vertical, then all points lie on it have the same x-coordinates

If line L is a vertical line and passes through the point (a, b), then its equation is

Since the given line is a vertical line and passes through the point (-5, -3)

That means a = -5

Then its equation is

Work Shown:

area = length*width

length = area/width

length = 162/9

length = 18 meters

option a , c and d are the correct statement or is a proper interpretation of a 95% confidence interval 95% of the population values will fall within this variable

What is the 95% confidence interval for a population mean?

It means that for any given number of samples, 95% of them will fall within 2 standard errors of the true mean of the population the sample is derived from.

a. In 95% of all samples, the sample mean will fall within 2 standard errors of the true population mean.

c. In 95% of all samples, the true population mean will be within 2 standard errors of the sample mean.

d. 95% of the population values will lie within 2 standard errors of the sample mean.

therefore option a , c and d are correct

learn more about of mean here

https://brainly.com/question/24071798

#SPJ4

Answer:

The slope is 5/7.

Step-by-step explanation:

Use a slope formula.

Slope:

\(\sf{\dfrac{y_2-y_1}{x_2-x_1} }\)

y₂ = (17)

y₁ = (7)

x₂ = (18)

x₁ = (4)

Rewrite the problem down.

\(\sf{\dfrac{17-7}{18-4}=\dfrac{10}{14}={\dfrac{10\div2}{14\div2}=\boxed{\sf{\dfrac{5}{7}}}\)

Therefore, the slope is 5/7.

I hope this helps! Let me know if my answer is wrong or not.

Answer:

5/7

Step-by-step explanation:

m=(y2-y1)/(x2-x1)

m=(17-7)/(18-4)

m=10/14

simplify

m=5/7

Answer:

Step-by-step explanation:

no because each y value doesn’t increase uniformly

Answer: false

Step-by-step explanation:

The x and y both have to have to same number between each by the y doesn’t