Consider the traffic light at the intersection of Sth Avenue and Meyran Avenue The probability of getting a green light on your way home at a given time you always leave at the same time) is 0.35 and that of yellow light is 0.04 (a) (1 point) What is the probability of getting either a green or a yellow light on a randomly chosen day? a (b) (Iphint) What is the probability of not getting a green light? (e) (l point) What is the probability of nding a red light on both Monday and Tuesday? (d) (1 point) What is the probability that you don't encounter red light until Wednesday starting Monday? (e) ( point) What is the probability of getting a green light on Wednesday given you had a red light on Tuesday?
Answers
a) Probability P(green or yellow) = 0.39 and b) P(not green) = 0.65 and c) This part of the question cannot be answered and d) P(green or yellow on Mon and Tue) × P(green on Wed) = 0.0523 and e) We cannot answer this part of the question.
(a) The probability of getting either a green or a yellow light on a randomly chosen day is given by the sum of their respective probabilities:
P(green) = 0.35 and P(yellow) = 0.04; hence the required probability is:
P(green or yellow) = P(green) + P(yellow) = 0.35 + 0.04 = 0.39.
(b) The probability of not getting a green light is equal to getting either a yellow or a red light. Hence, we have:
P(not green) = P(yellow or red) = 1 - P(green) = 1 - 0.35 = 0.65.
(c) To find the probability of finding a red light on both Monday and Tuesday, we need more information. This information is not given in the question. Hence, this part of the question cannot be answered.
(d) The probability of not encountering a red light until Wednesday starting Monday is the probability of getting either a green or yellow light on Monday and Tuesday and getting a green light on Wednesday. This is given by:
P(green or yellow on Mon and Tue) × P(green on Wed) = (P(green) + P(yellow))^2 × P(green) = (0.35 + 0.04)^2 × 0.35 = 0.0523.
(e) The probability of getting a green light on Wednesday given you had a red light on Tuesday is given by:
P(green on Wed | red on Tue) = P(green and red on Wed and Tue) ÷ P(red on Tue).
We don't have any information about the probability of getting a green and red light on Wednesday and Tuesday, so we cannot answer this part of the question.
To know more about Probability visit:
https://brainly.com/question/31828911
#SPJ11
Related Questions
I need helppppp please
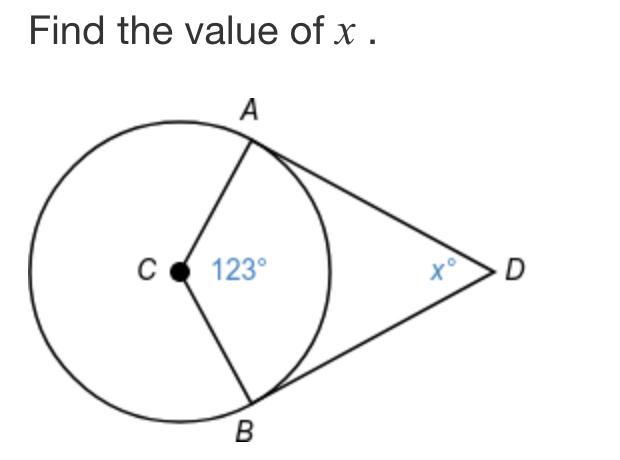
Answers
The measure of the angle x will be 57°.
The angle of an arc in a circle is defined as the angle subtended by the arc at the centre of the circle. The angle of the arc is measured in degrees or radians.
There is a theorem related to the angle of an arc in a circle called the central angle theorem. This theorem states that the angle subtended by an arc at the centre of a circle is equal to double the angle subtended by the same arc at any point on the circumference of the circle.
The measure of the angle x is,
x = ( 360 - 123 - 123 ) / 2
x = 57°
Hence, the value of an angle x is 57°.
To know more about the arc of a circle follow
https://brainly.com/question/23394322
#SPJ1
HELP!!! 35 POINTS Solve the equation. −7.8x=−1.56. x=?
Answers
Answer:
x = 0.2
Step-by-step explanation:
-7.8x = -1.56
-1.56/-7.8 = 0.2
x = 0.2
Answer:
\(x =\frac{1}{5}\) or \(0.2\) (they're the same)
Step-by-step explanation:
Divide each side by -7.8, so it now looks like this: x = 0.2Bobinvested$6500intoamutualfund with 3.5% monthly interest rate. What is the balance in the account after one month?
Answers
Answer:
$6727.50
Step-by-step explanation:
35/1000*6500
= 35*6.5
=227.50
6500+217.50
6727.50
Have to find x,y and z.

Answers
Answer:
z= 2√2
x=2
y=2√2
How many solutions does the equation 22 = 81 have?
Why does the equation have this many solutions?
Help me plzzzz
Answers
Answer:
No solutions.
Step-by-step explanation:
22 does not equal 81, so therefore no solutions.
Two bottled waters and an order of cheese costs $5.50. Three bottled waters and two orders of cheese nachos costs $9.50.
Answers
The cost of each nachos is $2.50 and the cost of each water bottle is $1.50.
What is a linear system of equations?
A system of linear equations consists of two or more equations made up of two or more variables such that all equations in the system are considered simultaneously. The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently.
Let x be the cost of each water bottle and y be the cost of each nachos.
Two bottled water and an order of cheese nachos costs $5.50.
So, 2x+y=5.50 -------(I)
Three bottled water and two orders of cheese nachos costs $9.50
3x+2y=9.50 -------(II)
Multiply equation (I) by 2, we get
4x+2y=11 -------(III)
Subtract equation (II) from equation (III), we get
4x+2y-(3x+2y)=11-9.50
x=$1.50
Substitute x=1.50 in equation (I), we get
2(1.50)+y=5.50
y=$2.50
Therefore, the cost of each nachos is $2.50.
The probability of A is 3/5, the probability of B is 15/16. The probability of A intersection B is 9/16. Are A and B independent events?
Answers
Answer:
P(A or B) = P(A) + P(B) - P(A and B)
= 3/5 + 15/16 - (3/5)(15/16)
= 48/80 + 75/80 - 45/80
= 78/80
So A and B are not independent events because P(A and B) is not equal to 1.
3+6/2+2-3•2 you must show your work
Answers
Answer:
your answer is 2.
Step-by-step explanation:
3+6/2+2-3*2
3+3+2-3*2
3+3+2-6
6+2-6
8-6
2
Basically, follow PEMDAS (parenthesis, exponents, multipulcation, division, addition, and subtraction.) You move from left to right, Always remember that, ok.
0 0
U
Select the correct answer.
What is the solution to the equation?
2(x + 7) = 8
OA. -15 and 1
OB. -15
OC. 1
OD.
no solution
Answers
Answer:
Option D is correct.
No solution
Step-by-step explanation:
2(x+7)=8
Apply 2 into bracket:
2x+14=8
2x=8-14
2x=-6
Divide both sides by 2:
x=-3
hence here is no option for x=-3, so answer is no solution.
what is another formula for finding the rate of discount?
Answers
Answer:
Subtract the final price from the original price. Divide this number by the original price. Finally, multiply the result by 100.
Step-by-step explanation:
The parking garage has 9 rows with 10 parking spaces in each row. There are 8 empty spaces.How many spaces are filled?
Answers
Answer:
82
Step-by-step explanation:
&&'&_555555555----&&&&---
Answer:
9X10-8=82
Step-by-step explanation:
Which could be the function graphed below?

Answers
Step-by-step explanation:
sqrt(x+4)
the answer is in the image above

i need help ( 3 images )



Answers
The probability of pulling a blue marble and the coin landing tail up will be C. 540 / 2500
How to calculate the probabilityProbability simply means the chance that a particular thing or event will happen. It is the occurence of likely events. It is simply the area of mathematics that deals with the numerical estimates of the chance that an event will occur or that a particular statement is true.
The probability of pulling a blue marble and the coin landing tail up will be:
= 18/50 × 30/50
= 540 / 2500
Learn more about probability on:
brainly.com/question/24756209
#SPJ1
find p percent in which sp = 14000 and cp = 16000
Answers
Answer:
percentage loss is 12.5%
Step-by-step explanation:
Find p percent in which sp = 14000 and cp = 16000
Given
Selling price = 14000
Cost price = 16000
Since CP>SP, there is a loss. We need to calculate the loss percent using the formula;
%Loss = CP-SP/CP * 100%
%Loss = 16000-14000/16000 * 100
%Loss = 2000/16000 * 100
%Loss = 1/8 * 100
%Loss = 12.5%
Hence the percentage loss is 12.5%
Quadrilaterals DONT and WALK are similar. Find the length of side DO.
(15 Points)
Send ASAP PLSS

Answers
X/3=15/5
45/5
x=9
So answer B
Two grains weighing 100kg 250 g and 150kg 250g are mixed and packed equally in 15 bags. Find the weight of each bag.
a.16.8 kg (b) 16.7 kg (c) 17 kg (d) 20 kg
Answers
Answer:
(B) 16.7 kg
Step-by-step explanation:
First, start by converting everything to kilograms (using unit converters):
\(250g(\frac{10^{-3}kg}{1g})=250*10^{-3}kg=0.25kg\)
Then, add all the weights together:
\(100kg+0.25kg+150kg+0.25g=250kg+0.5kg=250.5kg\)
Now, divide this number by 15 (since they are packed in 15 bags):
\(\frac{250.5kg}{15}=16.7 kg\)
(B) 16.7 kg
Help meeeeee plss !!!!
Multiple choices
A) 5
B) 25
C) 36
D) 21
E) 3
F) 55

Answers
Answer:
D)21
Step-by-step explanation:
I hope I can help. You won't make a mistake there
Answer:
Answer is D) 21
\({ \tt{ {x}^{2} - 7x + 3 = 0}}\)
Sum of roots [L + M]: -(-7) = 7
Product of roots [ LM ]: 3
\({ \rm{L {}^{2} M +LM {}^{2} = LM(L + M )}} \\ \\ = { \rm{3(7)}} \\ \\ = 21\)
The perimeter of the polygon is 12 in. What is the length of side x?
Answers
Answer:
2in
Step-by-step explanation:
Since we are not given the type of polygon, let the polygon be an hexagon. An hexagon is a 6 sides shape. The perimeter of the shape will be the sum of all the sides of the polygon
Perimeter of the polygon = 6L
Length is the length of the side
Given
Perimeter of the polygon = 12in
Substitute and get L
P = 6L
12 = 6L
L = 12/6
L = 2in
Hence the length of side x of the polygon is 2in
please help with the questions below

Answers
The asymptotes of the reciprocal function are x = 3 and y = 4. Also, the domain is x < 3 or x > 3 and the range is y < 4 or y > 4
How to determine the values of a, c, d and k?The function is given as:
f(x) = -2[1/0.5(x -3)] + 4
A reciprocal function is generally represented as:
f(x) = a[1/(x -c)] + k
So, we have:
a = -2
c = -3 * 0.5
c = -1.5
k = 4
d = 0
Hence, the values of a, c, d and k are -2, -1.5, 0 and 4
The asymptotesWe have:
f(x) = -2[1/0.5(x -3)] + 4
Set the radical to 0
y = 0 + 4
Evaluate
y = 4
Set the denominator to 0
x - 3 = 0
Evaluate
x = 3
Hence, the asymptotes are x = 3 and y = 4
The graph of the functionSee attachment for the graph of the function f(x) = -2[1/0.5(x -3)] + 4
The table of values is
x y
-4 4.6
-2 4.8
2 8
4 0
From the graph of the function, the domain is x < 3 or x > 3 and the range is y < 4 or y > 4
Read more about functions at:
https://brainly.com/question/2328150
#SPJ1

use the method of variation of parameters to solve the initial value problem x' = ax f(t), x(a) = xa using the following values. 4 -2 16t2 0 1 2t - 40 a= f(t) = x(0) = 2 - 1 4t t 1-2t x(t) =
Answers
The process involves finding the complementary solution x_c(t) by solving the homogeneous equation, determining the particular solution x_p(t) using the method of variation of parameters, and combining them to obtain the general solution x(t).
1. The method of variation of parameters can be used to solve the initial value problem x' = axf(t), x(a) = xa, where a and f(t) are given functions. In this case, we have the values a = 4 - 2t and f(t) = 16t^2. We need to find the solution x(t) using the initial condition x(0) = 2.
2. To solve the initial value problem using the method of variation of parameters, we first find the complementary solution x_c(t) by solving the homogeneous equation x' = ax.
3. For the given a = 4 - 2t, the homogeneous equation becomes x' = (4 - 2t)x. By separation of variables and integration, we find the complementary solution x_c(t) = Ce^(2t - t^2).
4. Next, we find the particular solution x_p(t) by assuming a particular solution of the form x_p(t) = u(t)e^(2t - t^2), where u(t) is a function to be determined.
5. Differentiating x_p(t) and substituting it into the original differential equation, we can solve for u'(t) and determine the form of u(t). After finding u(t), we substitute it back into x_p(t).
6. Finally, the general solution is given by x(t) = x_c(t) + x_p(t). By substituting the values and integrating, we can obtain the specific solution x(t) for the given initial condition.
Learn more about homogeneous equation here: brainly.com/question/12884496
#SPJ11
CAN YOU PLEASE HELP ME!!!!!!!!

Answers
Answer:
Step-by-step explanation:

Answer:
try desmos!
Step-by-step explanation:
put it into the desmos graphing calculator

PLS HELP ME ILL GIVE YOU BRAINIEST

Answers
what is (4x6) x (3-2)
Answers
Answer: 24
Step-by-step explanation: do 4 times 6 first then 3-2 and then times it and you get 24
Suppose that f(x) = a + b and g(x) = f^-1(x) for all values of x. That is, g is
the inverse of the function f.
If f(x) - g(x) = 2022 for all values of x, determine all possible values for an and b.
Answers
Given: $f(x) = a + b$ and $g(x) = f^{-1}(x)$ for all $x$Thus, $g$ is the inverse of the function $f$.We need to find all possible values of $a$ and $b$ such that $f(x) - g(x) = 2022$ for all $x$.
Now, $f(g(x)) = x$ and $g(f(x)) = x$ (as $g$ is the inverse of $f$) Therefore, $f(g(x)) - g(f(x)) = 0$$\ Right arrow f(f^{-1}(x)) - g(x) = 0$$\Right arrow a + b - g(x) = 0$This means $g(x) = a + b$ for all $x$.So, $f(x) - g(x) = f(x) - a - b = 2022$$\Right arrow f(x) = a + b + 2022$Since $f(x) = a + b$, we get $a + b = a + b + 2022$$\Right arrow b = 2022$Therefore, $f(x) = a + 2022$.
Now, $g(x) = f^{-1}(x)$ implies $f(g(x)) = x$$\Right arrow f(f^{-1}(x)) = x$$\Right arrow a + 2022 = x$. Thus, all possible values of $a$ are $a = x - 2022$.Therefore, the possible values of $a$ are all real numbers and $b = 2022$.
For more such questions on values
https://brainly.com/question/26352252
#SPJ8
whats the area of 8ft, 6ft and 2ft?
Answers
Answer:
96
Step-by-step explanation:
8x6=48
48x2=96
What is the measure of DEF? Pls help me asap

Answers
Step-by-step explanation:
3y +4 =5y -10
2y = 14
y = 7
DEF = (3Y+4)× 2 OR (5Y-10) ×2 OR (5Y-10+ 3Y+4)
Def= (3 ×7+4)×2
=50 degree
the indexed variables (members) of an array must be integers. true or false
Answers
It is true that the indexed variables (members) of an array must be integers.
The indexed variables or members of an array must be integers. This is because arrays are data structures that store elements in a contiguous block of memory, and each element is accessed using an index. Indexing allows us to uniquely identify and retrieve specific elements within the array. In most programming languages, including C, C++, Java, and Python, array indices are integers and must be whole numbers (positive or negative) without any fractions or decimals. Attempting to use non-integer values as indices would result in a compilation error or unexpected behavior.
To know more about integers,
https://brainly.com/question/29255714
#SPJ11
Solve -51/2+63/4+(-41/4)
Answers
Answer:
-20 is your answer
Step-by-step explanation:
If 18% of a number is 33, find 6% of that number
Answers
Answer:
11
Step-by-step explanation:
6 is 1/3 of 18
so, 6% is 1/3 of 18%
What’s the answer pls help

Answers
Answer:
m= - 3/2
c=1/2
Step-by-step explanation:
y=mx+c (formula for finding slope)
y= -3x/2+1/2
m= - 3/2
c=1/2