Consider the function f(x) = x/x²+1 Find the precise value of C such that Newton's Method will converge if any only if the seed is chosen so that Ixol

Answers
The largest value of C such that Newton's Method will converge if and only if |x₀| < C is C = 1.
What is the value of C for which the function converges?
To use Newton's Method to find a root of a function f(x), we need to start with a seed value x₀ and iterate using the formula:
xᵢ₊₁ = xᵢ - f(xᵢ) / f'(xᵢ)
where;
f'(x) is the derivative of f(x)The method will converge to a root of f(x) if the seed value x₀ is chosen close enough to the root.
To find the value of C such that Newton's Method will converge if and only if |x₀| < C for the function f(x) = x/(x²+1), we need to examine the behavior of the function and its derivative.
First, we compute the derivative of f(x):
f'(x) = (x²+1 - 2x²) / (x²+1)²
= (1-x²) / (x²+1)²
The roots of f(x) are the values of x such that f(x) = 0, which are x = 0.
We can check that f(0) = 0 and that f(x) is positive for x > 0 and negative for x < 0, which means that 0 is the only root.
To determine the behavior of f(x) and f'(x) near x = 0, we can use their Taylor series expansions:
f(x) = x/(x²+1) = x(1-x²+x⁴-...) = x - x³ + x⁵ - ...
f'(x) = (1-x²) / (x²+1)² = 1 - 4x² + 9x⁴ - ...
We can see that f(0) = 0 and f'(0) = 1, which means that x = 0 is a root of f(x) and that the derivative is nonzero at this point.
Therefore, by the convergence criterion for Newton's Method, if we choose a seed value x₀ close enough to 0, the method will converge to the root x = 0.
To find the value of C such that Newton's Method will converge if and only if |x₀| < C, we need to find the radius of the largest interval around x = 0 such that f(x) and f'(x) remain bounded away from 0.
Near x = 0, we can bound f(x) and f'(x) as follows:
|f(x)| = |x/(x²+1)| ≤ |x| (since x²+1 ≥ 1)
|f'(x)| = |(1-x²)/(x²+1)²| ≤ 1 (since x²+1 ≥ 1)
Therefore, if we choose a seed value x₀ such that |x₀| < 1, then both f(x₀) and f'(x₀) will be bounded away from 0, and Newton's Method will converge to the root x = 0.
On the other hand, if we choose a seed value x₀ such that |x₀| ≥ 1, then f(x₀) will be arbitrarily close to 0, and the method may not converge.
Learn more about convergence of function here: https://brainly.com/question/29851807
#SPJ1
The complete question is below:
Consider the function f(x) = x/(x²+1). Find the precise value of C such that Newton's Method will converge if and only if the seed is chosen so that
|x₀| < C.
Related Questions
Solve |x+4|=9. ..............
Answers
Can I get Brainly?

4x+7=23. explain the steps you would use to solve the equation for x.
Answers
Answer:
x=4
Step-by-step explanation:
1. isolate the variable by subtracting 7 on both sides: 4x=23-7
2. simplify: 4x=16
3. divide both sides by 4: x=16/4
4. simplify: x=4
Answer:
x=4
Step-by-step explanation:
4x+7=23
Collect like terms
4x=23-7
4x=16
Divide both sides by the co-efficient of x
4x/4=16/4
x=4
Cuánto es 1/4 mas 1/4
Answers
Answer:
0.5
Step-by-step explanation:
Solve for x
Select the correct response:
A: 14
B: 19.25
C: 10
D: 6.5

Answers
The value of the x is 10.
What is the exterior angle theorem?
The exterior angle theorem states that the measure of an exterior angle is equal to the sum of the measures of the two opposite(remote) interior angles of the triangle.
We have given,
angles of the triangle:
Interior angles :
∠D = 2x + 7,
∠E = 26°,
Exterior angle:
∠C = 6x - 7
To find x = ?
few common properties about the angles of a triangle:
A triangle has 3 internal angles which always sum up to 180 degrees.
It has 6 exterior angles and this theorem gets applied to each of the exterior angles.
Note that an exterior angle is supplementary to its adjacent interior angle as they form a linear pair of angles.
Exterior angles are defined as the angles formed between the side of the polygon and the extended adjacent side of the polygon.
So,
∠C = ∠D + ∠E
6x - 7 = 2x + 7 + 26,
6x - 7 - 2x - 7 = 26,
4x - 14 = 26,
4x = 40
x = 40/4
x = 10,
Hence, the value of the x is 10.
To learn more about the exterior angle theorem visit,
https://brainly.com/question/17307144
#SPJ1
Which unit is a derived unit?
O meter
Odensity
O ampere
O second
Answers
density
a derived unit is something that comes from using base units in mathematical operations.
\(3x^{2} +10x-8=0\\\)
Answers
The diagram shows a prism. Draw the front and side elevation of the prism on the grid. Use the scale 2 squares to 1m.
I know that the side elevation is correct but I can't get the front. Please help!

Answers
The sketch of the front elevation and the side elevation of the prism are added as an attachment
How to draw the front elevation and the side elevation of the prismFrom the question, we have the following parameters that can be used in our computation:
The prism
Using the figure as a guide, we understand that:
The front elevation is a rectangle of 2m by 0.5m
While the side elevation is a rectangle merged with a trapezoid
Next, we draw the elevations (see attachment)
Read more about prism at
brainly.com/question/23178481
#SPJ1

Find the integer pair that has the given product and sum. The product is 28 The sum is 11
Answers
Answer:
7 and 4
Step-by-step explanation:
when you multiply 7×4 the answer is 28 and when you add them the answer is 11.
I hope this helps
Answer:
4 and 7
Step-by-step explanation:
xy = 28 ..........1
x + y = 11........2
x = 11 - y.........3
substitute 3 in 1:
(11 - y)*y = 28
-y² + 11y - 28 = 0
y² - 11y + 28 = 0
( y - 7)( y - 4) = 0
y = 7 or y = 4
subs in 2:
x = 4 or x = 7
pairs: (4 ; 7) and (7 ; 4)
A drum of water is 3/4 full. When 9 litres are drawn from it, it is half full. How much water does the drum hold what is the capacity of the drum
Answers
Answer:
OK, Here is your answer
Step-by-step explanation:
Let's assume the capacity of the drum be C litres.Since the drum is initially 3/4 full, the amount of water in it is 3/4 × C = (3/4)C liters.When 9 liters of water are drawn from the drum, the remaining amount of water is (3/4)C - 9 liters.Since the drum is now half full, the amount of water remaining in it is (1/2)C liters.Therefore, we can write the equation: (3/4)C - 9 = (1/2)CTo solve for C, let's first get rid of the fractions by multiplying both sides by 4.(3/4)C - 9 = (1/2)C → 3C - 36 = 2C → C = 36Therefore, the capacity of the drum is 36 liters.Hence, the drum holds 3/4 × 36 = 27 liters of water initially and after 9 liters of water are drawn, the remaining amount of water in it is 27 - 9 = 18 liters.
Answer:
18 Lieters.
Step-by-step explanation:
found the answer in his answer. ↑↑↑↑
The product of 8 and the sum of a number m and 2 is 16
Answers
Step-by-step explanation:
8(m + 2)= 16
8m + 16 = 16
8m = 0
m = 0
At a pizza restaurant, a personal pizza has a radius of 10 centimeters and costs $5. Another restaurant takes a pizza with radius 30 centimeters, cuts it into 8 slices of equal area, and charges $5 per slice. Which is a better deal? Explain your reasoning.
Answers
Answer:
Remember that the area of a circle of radius R is given by:
A = pi*R^2
pi = 3.14
We know that:
Personal Pizza: radius = 10cm
price = $5
The area of pizza that you are getting is:
A = 3.14*(10cm)^2 = 314 cm^2
In the other case, we have a pizza with radius of 30 cm, cutted into 8 slices, such that each slice costs $5.
Then, if yo pay $5, the area of pizza that you get is an eight of the area of a circle of radius 30cm
This is:
A' = (1/8)*(3.14*(30cm)^2) = 353.25 cm^2
We can see that in the second case the area is larger, then the second option is the better deal, as you are getting a larger pizza area for the same price.
how do you find the length in feet of the boundary you’re given ?

Answers
find the conditional expectation of alpha x poisson and gamma distribution law of iterated expectation
Answers
The conditional expectation of αX given Y=y is (αλy / β + αλ)^α * e^(-(β+αλ)/βy) and the Law of Iterated Expectation gives E[αX] = (αλ / β + αλ)^α * (β / (β+αλ))^α * (Γ(α) / β).
Let X be a Poisson random variable with parameter λ and Y be a Gamma random variable with parameters α and β. We want to find the conditional expectation of αX given Y=y and then apply the Law of Iterated Expectation to find E[αX].
The conditional probability density function of αX given Y=y is:
fX|Y(x|y) = P(X=x|Y=y) = P(X=x,Y=y) / P(Y=y)
Since X and Y are independent, we have:
P(X=x,Y=y) = P(X=x)P(Y=y)
Therefore, the conditional probability density function of αX given Y=y is:
fX|Y(x|y) = (λ^x/x!) * (β^α / Γ(α)) * y^(α-1) * e^(-βy) / (λ^y * e^(-λ) * β^α / Γ(α))
fX|Y(x|y) = (λ^x / x!) * (y^α * e^(-βy)) / (Γ(α) * λ^y * β^α)
Now we can calculate the conditional expectation of αX given Y=y:
E[αX|Y=y] = ∑ x=0^∞ αx * fX|Y(x|y)
E[αX|Y=y] = ∑ x=0^∞ αx * (λ^x / x!) * (y^α * e^(-βy)) / (Γ(α) * λ^y * β^α)
E[αX|Y=y] = (αλy / β + αλ)^α * e^(-(β+αλ)/βy)
Now we can apply the Law of Iterated Expectation to find E[αX]:
E[αX] = E[E[αX|Y]]
E[αX] = E[(αλY / β + αλ)^α * e^(-(β+αλ)/βY)]
Since Y is a continuous random variable, we need to integrate over all possible values of Y:
E[αX] = ∫ 0^∞ (αλy / β + αλ)^α * e^(-(β+αλ)/βy) * (β^α / Γ(α)) * y^(α-1) * e^(-βy) dy
E[αX] = (αλ / β + αλ)^α * (β / (β+αλ))^α * (Γ(α) / β)
For such more question on expectation
https://brainly.com/question/24305645
#SPJ4
Compare the absolute value function g(x) modeled by the table and the function modeled by the equation, f(x)=−(x−3)2+9 . x g(x) −3 −4 −2 0 −1 4 0 8 1 12 2 8 What is the difference in the maximum values of g(x) and f(x) ? Select from the drop-down menu to correctly complete the statement.
Answers
The difference in the maximum values of the functions g(x) and f(x) is 3
How to determine the difference in the maximum values?The functions are given as
f(x) = -(x - 3)² + 9
Table of g(x)
x −3 −4 −2 0 −1 4
g(x) 0 8 1 12 2 8
The maximum value of f(x) is when the root expression is 0
i.e. -(x - 3)² = 0
So, we have
Max f(x) = 0 + 9
Max f(x) = 9
For the table of values, we have
Max g(x) = 12
The difference between these values is
Difference = 12 - 9
Evaluate
Difference = 3
Hence, the difference is 3
Read more about functions at
https://brainly.com/question/28277110
#SPJ1
Help me please (I have to write something to send a question)

Answers
Answer:
yshannmm
Step-by-step explanation:
yes
1.A(4,4), B(3, -1), C(1, -2); y-axis (; y x 0 B D4

Answers
The rule of a reflection across the y-axis is
\((x,y)\rightarrow(-x,y)\)So, let's transform each vertex.
\(\begin{gathered} A(4,4)\rightarrow A^{\prime}(-4,4) \\ B(3,-1)\rightarrow B^{\prime}(-3,-1) \\ C(1,-2)\rightarrow B^{\prime}(-1,-2) \end{gathered}\)Now, we graph the reflection, the image below shows it

6.1.3
What requirements are necessary for a normal probability distribution to be a standard normal probability distribution?
Answers
Answer:
The requirements that are necessary for a normal probability distribution to be a standard normal probability distribution are µ = 0 and σ = 1.
Step-by-step explanation:
A normal-distribution is an accurate symmetric-distribution of experimental data-values.
If we create a histogram on data-values that are normally distributed, the figure of columns form a symmetrical bell shape.
If X \(\sim\) N (µ, σ²), then \(Z=\frac{X-\mu}{\sigma}\), is a standard normal variate with mean, E (Z) = 0 and Var (Z) = 1. That is, Z \(\sim\) N (0, 1).
The distribution of these z-variates is known as the standard normal distribution.
Thus, the requirements that are necessary for a normal probability distribution to be a standard normal probability distribution are µ = 0 and σ = 1.
8 Annexure A RESEARCH TOOL: CAMPAIGN(S) IN THE COMMUNITY Name of a campaign: Position of the interviewee(s) at the Centre: ** Respond to the following questions/statements by placing a tick (✓) where appropriate and also by filling in the spaces below. 1. Does the Campaign pursue it's aims? YES/NO Elaborate
Answers
In the provided text is a questionnaire or form related to a research tool for assessing a campaign in the community.
The first question asks whether the campaign pursues its aims, with the options of answering "YES" or "NO." The respondent is then instructed to elaborate on their answer.
What is a questionnaire?A questionnaire is a research tool used to collect data by presenting a series of questions to respondents,typically in a written format.
Questionnaires are an important research tool as they allow researchers to gather large amounts of data from a large number of participants in a standardized and efficient manner.
They provide a structured approach to collecting information,allowing for easy analysis and comparison of responses.
Questionnaires can be used in various research settings and are particularly useful for collecting quantitative data,measuring attitudes, opinions, behaviors, and gathering demographic information.
Learn more about Research Tool at:
https://brainly.com/question/28982692
#SPJ1
a line has a slope of -6 and includes the points (g,-8) and (0,-2). What is the value of g?
Answers
Answer:
Step-by-step explanation:
Equation for line of slope -6 that passes through (0,-2):
y+2 = -6(x-0)
y = -6x - 2
Plug in (g,-8) and solve for g:
-8 = -6g - 2
g = 1
Which function has a greater maximum?
�
(
�
)
=
−
2
(
�
+
4
)
2
+
1
f(x)=−2(x+4)
2
+1f, left parenthesis, x, right parenthesis, equals, minus, 2, left parenthesis, x, plus, 4, right parenthesis, squared, plus, 1
A coordinate plane. The x- and y-axes both scale by one. The graph is the function y equals g of x which is a parabola that opens down. The function increases through negative four, negative five and negative three, negative two. It has a maximum at negative two, one, then the function decreases through negative one, negative two and zero, negative five.
Answers
The function f(x) = \(-2(x+4)^2\) + 1 has a greater maximum.
1. The given function is f(x) = \(-2(x+4)^2\) + 1.
2. To find the maximum of the function, we need to determine the vertex of the parabola.
3. The vertex form of a quadratic function is given by f(x) = \(a(x-h)^2\) + k, where (h, k) represents the vertex.
4. Comparing the given function to the vertex form, we see that a = -2, h = -4, and k = 1.
5. The x-coordinate of the vertex is given by h = -4.
6. To find the y-coordinate of the vertex, substitute the x-coordinate into the function: f(-4) = \(-2(-4+4)^2\) + 1 = \(-2(0)^2\) + 1 = 1.
7. Therefore, the vertex of the function is (-4, 1), which represents the maximum point.
8. Comparing this maximum point to the information provided about the other function g(x) on the coordinate plane, we can conclude that the maximum of f(x) = \(-2(x+4)^2\) + 1 is greater than the maximum of g(x).
9. The given information about g(x) is not sufficient to determine its maximum value or specific equation, so a direct comparison is not possible.
10. Hence, the function f(x) =\(-2(x+4)^2\) + 1 has a greater maximum.
For more such questions on maximum, click on:
https://brainly.com/question/29795588
#SPJ8
transformation of the graph of f(x)=x^3 for the graph of g(x)=-x^3
Answers
The transformation was a reflection over the x-axis. This is because \(g(x)=-f(x)\).
pls help me i need help

Answers
Answer:
3x was subtracted from the left side, but 3x was subtracted from the right side. The Subtract Property of Equality states that you can subtract the same number from each side and the equation will remain true. But 3x and 3 are not the same number (unless x is 1).
x = -8/5
Step-by-step explanation:
Step 1: Simplify both sides of the equation.
\((7x+3x)+(21)=5\) \(10x + 21 = 5\)Step 2: Subtract 12 from both sides.
\(10x + 21 - 21 = 5 - 21\) \(10x = -16\)Step 3: Divide both sides by 10.
\(\frac{10x}{10} = \frac{-16}{10}\) \(x = -\frac{8}{5}\)9514 1404 393
Answer:
3x31x = -1.6Step-by-step explanation:
You answer this sort of question by comparing each line to the line above to see what the differences are. In the second line, the term 3x is missing from the left side of the equal sign, and the value 5 has been changed to the value 2 on the right side. The wording of the statement you're to fill in tells you that it should read ...
3x was subtracted from the left side, but 3 was subtracted from the right side.
... 3x and 3 are not the same number (unless x is 1 .)
__
The correct solution is ...
7x +21 +3x = 5 . . . . . . given
10x +21 = 5 . . . . . . . . . collect terms
10x = -16 . . . . . . . . . . . subtract 21 from both sides
x = -1.6 . . . . . . . . . . . . divide both sides by 10
_____
Additional comment
It can often work well to "read ahead" when answering a question or series of questions. The later questions or comments often provide clues that help you understand how to answer the earlier questions.
Here, for example, it becomes clear that 3x and 3 were subtracted from the different sides of the equation. You can find that out simply by reading the rest of the statement you're to fill in. These are the answers to the questions asked in the first part of the statement.
Use the distributive property to remove the parentheses.

Answers
70x^7-14x^6+14x^2
Let z be a standard normal random variable. Use the calculator provided, or this table, to determine the value of c . 0.1112
Answers
DIRE NEED OF HELP, pleaseee help
(not a lot of points sorry)
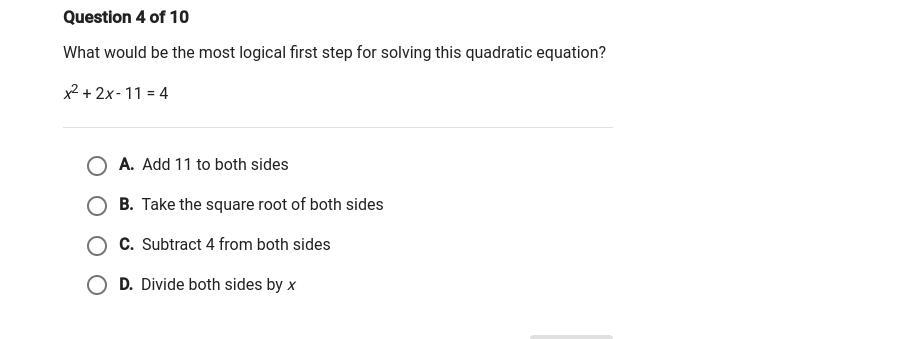
Answers
Answer:
C. Subtract 4 from both sides.
Step-by-step explanation:
You need the equation in the form x² + ax + b = 0 to then either try factoring or use the quadratic formula.
In order to achieve that, you need to first:
Subtract 4 from both sides.
Mary paid $12.24 for a 6.35-kg bag of dog food. A few weeks later, she paid $13.99 for a 7.48-kg bag at a different store.
Find the unit price for each bag. Then state which bag is the better buy based on the unit price.
Round your answers to the nearest cent.
Answers
Answer:
First bag's unit price=$1.92 per kg Second bag's unit price=$1.87 per kg
The second bag is the better deal
Step-by-step explanation:
Divide the price by the weight to get the unit price per kg
The lowest number is the better buy
Answer: First bag's unit price=$1.92 per kg Second bag's unit price=$1.87 per kg
Step-by-step explanation:
Show the solution in each linear inequality in system of linear inequalities by graphing y>-7/2x+3
Answers
Answer: When you graph it, put a dot on 3, and then count down 7 spaces, and 2 spaces to the right, put a dot there. Use a straight edge to draw a line through the two dots, that continues on the graph. You can continue to got down 7, over 2 if needed.
Step-by-step explanation:
Write an equation of the line passing through
(-1.5) and (3,5). Give the answer in standard
form Ax+By=C
Answers
9514 1404 393
Answer:
y = 5
Step-by-step explanation:
The given points lie on the horizontal line ...
y = 5
__
You could write this as 0x+1y=5, but the conventions regarding coefficients of 0 and 1 would have this simplified to y=5.
ompute the amount to be paid for each of the four separate invoices assuming that all invoices are paid within the discount period. Terms Payment $ Merchandise (gross) a. $ 8,000 24,500 C. 81,000 17,500 I 2/10, n/60 1/15, EOM 1/10, n/30 3/15, n/45 7,840 20,825 72,900 14,875
Answers
Where the above Terms exists, the amount to be paid in each of the above invoices are given as follows;
Invoice 1: $7,840Invoice 2: $24,255Invoice 3: $80,190Invoice 4: $16,975.How would one define the the Terms above?Note that the terms are defined as follows;
Terms A: 2/10, n/60 (2% discount if paid within 10 days, net due in 60 days)
Terms B: 1/15, EOM (1% discount if paid within 15 days, end of month terms)
Terms C: 1/10, n/30 (1% discount if paid within 10 days, net due in 30 days)
Terms D: 3/15, n/45 (3% discount if paid within 15 days, net due in 45 days.
So to compute the amount to be paid for each of the four separate invoices assuming that all invoices are paid within the discount period, we need to calculate the amount of the discount and subtract it from the gross merchandise amount.
For terms 2/10, n/60:
Discount = 2% of $8,000 = $160
Amount to be paid = $8,000 - $160
= $7,840
For terms 1/15, EOM:
Discount = 1% of $24,500 = $245
Amount to be paid = $24,500 - $245
= $24,255
For terms 1/10, n/30:
Discount = 1% of $81,000 = $810
Amount to be paid = $81,000 - $810
= $80,190
For terms 3/15, n/45:
Discount = 3% of $17,500 = $525
Amount to be paid = $17,500 - $525
= $16,975
Therefore, the amount to be paid for each of the four separate invoices assuming that all invoices are paid within the discount period are:
Learn more about Payment terms:
https://brainly.com/question/24086159
#SPJ1
A piece of material measures 38 inches. Courtney cuts the piece of material into two pieces. One piece measures 19 inches. Write an addition equation that could be used to find the length, m, of the other piece of material.
Answers
Answer:
As a whole, the piece first measured 38 inches. No matter how many times you cut it, all of the pieces will still add up to 38 inches. You know that 19 inches is the length of one of the two pieces, so all you need to find is the other unknown piece. Add the two together, with m being the unknown length.
19+m=38
If you want to solve the equation, just subtract 19 from both sides.
19+m=38
m=19