Common sources of caffeine in the diet are coffee and tea. suppose that 75 people were surveyed: 50 adults drink coffee, 30 adults drink tea, and 15 drink both coffee and tea. what percentage of adults drink either coffee or tea?
Answers
The correct answer is approximately 86.67% of adults surveyed drink either coffee or tea.
To determine the percentage of adults who drink either coffee or tea, we need to add the number of adults who drink coffee and the number of adults who drink tea and subtract the number of adults who drink both.
Number of adults who drink either coffee or tea = Number of adults who drink coffee + Number of adults who drink tea - Number of adults who drink both
= 50 + 30 - 15
= 65
Out of the total 75 people surveyed, 65 adults drink either coffee or tea. To find the percentage, we divide the number of adults who drink either coffee or tea by the total number of adults surveyed and multiply by 100.
Percentage of adults who drink either coffee or tea = (65 / 75) * 100
≈ 86.67%
Therefore, approximately 86.67% of adults surveyed drink either coffee or tea.
Learn more about percentage here:
https://brainly.com/question/24877689
#SPJ11
Related Questions
Do these ratios form a proportion?
5 boys to 7 girls
20 boys to 28 girls
yes or no
Answers
Answer:
yes
Step-by-step explanation:
First we should find a GCF for the number of boys and girls.
The gcf for the two would be 4.
Divide.
20/4 = 5
28/4= 7
therefore the ratio for boys to girls would be 5 to 7
NEED HELP ASAP NO LINKS!!!!!!!
On the first day it was posted online, a music video got 1500 views. The number of views that the video got each day increased by 18% per day. How many total views did the video get over the course of the first 27 days, to the nearest whole number?
Answers
Answer:
48
Step-by-step explanation:
18% of 1500 is 270
270x18% is 48.6 since it increased by 18%
Complete the table of values. Please help!

Answers
Answer:
Step-by-step explanation:
Where we have "x" must replace for the number shown on table
We have for "x" tha numbers: 0; 1; 2; 3; 4 and 5
Equation:
1.y = x+4
y = x + 4
For x = 0
y = x + 4
y = 0 + 4
y = 4
For x = 1
y = x + 4
y = 1 + 4
y = 5
For x = 2
y = x + 4
y = 2 + 4
y = 6
For x = 3
y = x + 4
y = 3 + 4
y = 7
For x = 4
y = x + 4
y = 4 + 4
y = 8
For x = 5
y = x + 4
y = 5 + 4
y = 9
So:
x y
0 4
1 5
2 6
3 7
4 8
5 9
I hope help you.
Jerome's favorite Harry Potter book has 222222 chapters, 500500500 pages, and approximately 100{,}000100,000100, comma, 000 words. He's curious how many of the words are "made up" words or names that don't exist in the dictionary.
He wants to take a systematic random sample of about 500500500 words to estimate what percent of the words in the book are made up.
Which of these strategies will accomplish his intended design?
Choose 1 answer:
Choose 1 answer:
(Choice A)
A
Randomly select one of the first 202020 words and every 20^\text{th}20
th
20, start superscript, start text, t, h, end text, end superscript word thereafter for the sample.
(Choice B)
B
Randomly select one of the first 200200200 words and every 200^\text{th}200
th
200, start superscript, start text, t, h, end text, end superscript word thereafter for the sample.
(Choice C)
C
Randomly select 232323 words from each chapter.
(Choice D)
D
Randomly select 111 word from each page.
(Choice E)
E
Assign every word a number and use a computer to randomly select 500500500 numbers with no repeats
Answers
Using sampling concepts, it is found that a systematic sampling of 500 words would be achieved as follows:
B. Randomly select one of the first 200 words and then every 200th word thereafter for the sample.
How are samples classified?Samples may be classified as:
Convenient: Drawn from a conveniently available pool.Random: All the options into a hat and drawn some of them.Systematic: Every kth element is taken. Cluster: Divides population into groups, called clusters, and each element in the cluster is surveyed.Stratified: Also divides the population into groups. Then, a equal proportion of each group is surveyed.In this problem, he wants a systematic sampling, hence he should choose every kth word, which means that the answer is between options a and b.
He will choose 500 words out of 100,000, hence the value of k is given by:
k = 100000/500 = 200.
Which means that option B is correct.
More can be learned about sampling concepts at https://brainly.com/question/25122507
Answer:
B
Step-by-step explanation:
khan
The length of a warm is 3.25 inches right as a fraction in simplest form
Answers
Answer:
13/4 inches
Step-by-step explanation:
3.25 inches
325/100 inches
13/4 inches
Find the simplified product: 2 square root of 5x^3(-3 square root of 10x^2)

Answers
Answer:
Step-by-step explanation:
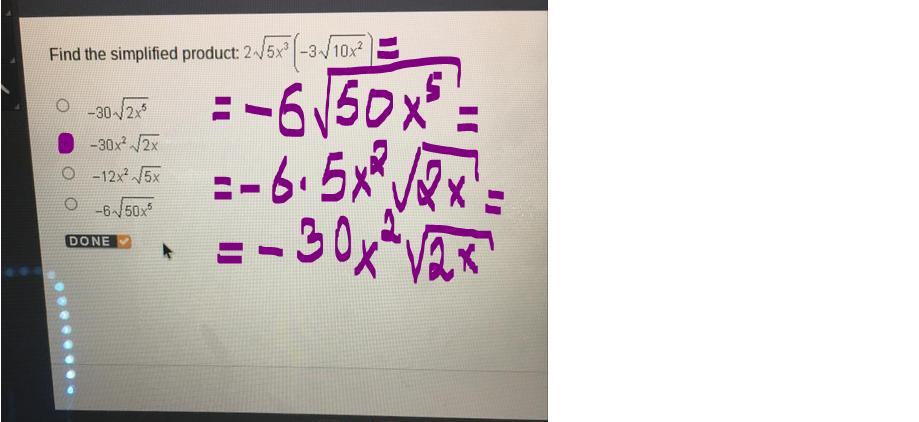
Last Wednesday, students could choose ham or turkey sandwiches for lunch. The cafeteria made 50 sandwiches in all, 5 of which were turkey. What percentage of the sandwiches were turkey sandwiches?
Answers
Answer:
90%
Step-by-step explanation:
50%×2 100%
5%×2 10%
45%×2 90%
The binomial distribution is used when
Answers
When there are precisely two outcomes of a trial that are mutually exclusive, the binomial distribution is used.
A discrete distribution is the binomial distribution. It is a probability distribution that is frequently utilised. It is then designed to represent a variety of distinct phenomena that appear in business, social sciences, natural sciences, and medical research.
The probability of achieving a specific number of successes, such as successful basketball shots, out of a fixed number of trials can be determined using the binomial distribution. To determine discrete probabilities, we use the binomial distribution.
To know more about binomial distribution, visit,
https://brainly.com/question/29163389#:~:text=Expert%2DVerified%20Answer&text=Binomial%20distribution%3A,conditions%20are%20satisfied%20or%20not.
#SPJ4
What is the area of the triangle?
4
:10
2
units

Answers
Answer:
Your answer is 20
Step-by-step explanation:
as the formula 1/2*4*10=20.
hope it help you if yes then please make me the brainiest.
Thank you
parshv
3k/2 - k+3/3 = 8- k+2/4
answer is 6
cud someone help me y dis is da answer
Answers
Answer:
k = 6
Step-by-step explanation:
\(\frac{3k}{2}\) - \(\frac{k+3}{3}\) = 8 - \(\frac{k+2}{4}\)
multiply through by 12 ( the LCM of 2, 3 and 4 ) to clear the fractions
18k - 4(k + 3) = 96 - 3(k + 2) ← distribute parenthesis on both sides
18k - 4k - 12 = 96 - 3k - 6
14k - 12 = - 3k + 90 ( add 3k to both sides )
17k - 12 = 90 ( add 12 to both sides )
17k = 102 ( divide both sides by 17 )
k = 6
Select the methodology that would result in a subjective probability....
Dividing the number of favorable events by the number of possible events.
Studying the fraction of times in the past a particular event has happened.
Weighing the available information and assigning a probability.
Answers
Weighing the available information and assigning a probability.
A sort of probability called subjective probability is one that is based on a person's subjective assessment or personal knowledge of the likelihood of a particular result. It solely represents the subject's thoughts and prior experience and does not include any formal computations. A "gut instinct" used when making a deal is an illustration of subjective probability.
So, as per the definition of subjective probability
Dividing the number of favourable events by the number of possible events and Studying the fraction of times in the past a particular event has happened, both can be determined through calculations mathematically accurate but for Weighing the available information and assigning a probability we might use a "gut instinct". Thus
Weighing the available information and assigning a probability.
To learn more about subjective probability, visit
brainly.com/question/14743062
#SPJ4
A student claims that the sum of a rational number and an irrational number is always irrational. Is the claim correct? No. The claim is incorrect because 2 + √ 4 = 2 + 2 = 4 , and 4 is a rational number. No. The claim is incorrect because 2 plus square root of 4 is equal to 2 plus 2 is equal to 4, and 4 is a rational number. No. The claim is incorrect because 2 + 1 √ 4 = 2 + 1 2 = 5 2 , and 5 2 is a rational number. No. The claim is incorrect because 2 plus the fraction with numerator 1 and denominator square root of 4 is equal to 2 plus 1 half is equal to 5 halves, and 5 halves is a rational number. Yes. The claim is correct because 3 π + 4 π = 7 π , and 7 π is an irrational number. Yes. The claim is correct because 3 pi plus 4 pi is equal to 7 pi, and 7 pi is an irrational number. Yes. The claim is correct because √ 16 + π = 4 + π , and 4 + π is an irrational number. Yes. The claim is correct because square root of 16 plus pi is equal to 4 plus pi, and 4 plus pi is an irrational number.
Answers
The correct option regarding whether the sum of a rational number and an irrational number is always irrational is given by:
Yes. The claim is correct because √ 16 + π = 4 + π , and 4 + π is an irrational number.
What are rational and irrational numbers?Rational numbers are numbers that can be represented by fractions, such as terminating decimals.Irrational numbers are numbers that cannot be represented by fractions, such as non-terminating decimals and non-exact roots.
The sum of a terminating decimal with a non-terminating decimal always results in a non terminating decimal, that is, the sum of a rational number with an irrational number is always irrational, and the correct option is given by:
Yes. The claim is correct because √ 16 + π = 4 + π , and 4 + π is an irrational number.
More can be learned about rational and irrational numbers at brainly.com/question/17232771
#SPJ1
(-4)(-19) (-2) help I’m 4 lessons behind
Answers
Answer: -152
Step-by-step explanation:
(-4)(-19)(-2)=
(-4)*(38)=
-152
Graph the image of U(2, -4) after a translation 8 units right.

Answers
Explanation:
Given point: (2, -4)
A movement to the right will be an addition to the x coordinate
y coordinate = -4
x coordinate = 2
8 units to the right implies an addition of 8 units to the x-coordiante
new x - coordinate = 2 + 8 = 10
The new coordinate (x, y) = (10, -4)
plotting on the graph:
A population has a mean of 180 and a standard deviation of 36. A sample of 84 observations will be taken. The probability that the sample mean will be between 181 and 185 is?.
Answers
The probability that the sample mean will be between 181 and 185 is 0.3039.
Given,
The mean of a population, μ = 180
Standard deviation, σ = 36
Number of sample observations, n = 84
We have to find the probability that the sample mean will be between 181 and 185;
Lets convert 181 and 185 into z scores;
z = (x - μ) / (σ/√n)
x = 181z = (181 - 180) / (36/√84)
z = 1/3.93
z = 0.25
x = 185z = (185 - 180) / (36/√84)
z = 5 / 3.93
z = 1.27
Lets look z score table;
The area to the left of z = 0.25 is 0.5987
The area to the left of z = 1.27 is 0.8980
The probability that the z is between 0.25 and 1.27 would be 0.8980 – 0.5887 = 0.3039.
That is,
The probability that the sample mean will be between 181 and 185 is 0.3039.
Learn more about probability here;
https://brainly.com/question/6598268
#SPJ4
Calculate B(4,5) if B(a,b) = 3a + 7b.
Answers
We were given a function with the following expression:
\(B(a,b)\text{ = 3a + 7b}\)And we need to calculate the value of this function for a pair of inputs. In this case a = 4 and b = 5. So we have:
\(\begin{gathered} B(4,5)\text{ = 3}\cdot4\text{ + 7}\cdot5 \\ B(4,5)\text{ = 12 + 35} \\ B(4,5)\text{ = 47} \end{gathered}\)A boy is launching a toy rocket he got for his birthday from the top of an 80 ft building. The function representing
the height is f(0) = -16x? +64x + 80 where x represents time in seconds.
How many seconds did it take the rocket to reach it's maximum height?
A
144 sec
B)
2 sec
Eliminate
1.5 sec
D)
128 sec

Answers
Answer:
2 seconds, assuming the "?" in the equation is supposed to be ^2 (the exponent of 2): f(h) = -16x^2 +64x + 80
Step-by-step explanation:
You can either graph the functuion or take the first derivative to find the maximum height. The first derivative will give us the slope for a values of x. The slope at the top height of the rocket is zero, since it has stopped and is starting it's way back down.
First Derivative:
f(x) = -16x^2 +64x + 80
f'(x) = -32x + 64
Set this equal to zero and solve for x
0 = -32x + 64
x = 2 seconds.
Use 2 seconds in the original equation to find the height at 2 seconds.
f(2) = -16x^2 +64x + 80
f(2) = -16(2)^2 +64*(2) + 80
f(2) = 144 feet
Graph:
A graph is attached. You can locate the maximum at (2,144)

Are the lines (-6,-2) and (2,3) perpendicular ?
Answers
Answer:
Step-by-step explanation:
No
use the greens theorem to evaluate the integral of sqrt(1 x^3)dx 2xydy Where C is the path vith vertices (0,0), (1,0), and (1,3) oriented CCW
Answers
The value of the line integral is 1/3.
To use Green's theorem to evaluate the line integral, we need first to find the curl of the vector field (M, N):
M = √(1-\(x^{3}\))dx
N = 2xydy
Taking partial derivatives of M and N with respect to x and y, respectively, we get:
∂M/∂y = 0
∂N/∂x = 2y
So the curl of (M, N) is:
curl(M,N) = ∂N/∂x - ∂M/∂y = 2y
Now we can apply Green's theorem:
∮C (M dx + N dy) = ∬R curl(M,N) dA
where C is the oriented boundary of the region R.
The region R is the triangle with vertices(0,0), (1,0), and (1,3).
We can express R as:
R = {(x,y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 3x}
The integral on the right-hand side of Green's theorem can be evaluated using iterated integrals:
∬R curl(M,N) dA
= ∫x=0..1 ∫y=0..3x 2y dy dx
= ∫x=0..1 \(x^{2}\) dx
= 1/3
So the line integral is:
∮C (M dx + N dy) = ∬R curl(M,N) dA = 1/3
Therefore, the value of the line integral is 1/3.
know more about Green's theorem here:
https://brainly.com/question/30080556
#SPJ11
A car travelling at 30 km/h takes 40 minutes to complete a journey. How long would it take if it
travelled at 60 km/h?
Answers
Answer: 20 Minutes
Step-by-step explanation:
If you are traveling double the speed, the end time is going to be half of the original time.
Find dy/dx if y = ln(e^x^2+1)+e sin x
Answers
dy/dx = (1/(e^(x^2)+1)) * (e^(x^2) * 2x) + e*cos(x)
This is the derivative of the given function y with respect to x.
We want to find the derivative dy/dx of the function y = ln(e^(x^2)+1) + e*sin(x). To do this, we will apply the rules of differentiation.
First, we'll differentiate the function term-by-term. For the natural logarithm function, the derivative is (1/u) * du/dx, where u is the function inside the natural logarithm. In our case, u = e^(x^2) + 1.
The derivative of e^(x^2) is found by applying the chain rule, which gives us (e^(x^2) * 2x). The derivative of 1 is 0. Therefore, the derivative of u is (e^(x^2) * 2x). Now we can find the derivative of ln(u):
d[ln(u)]/dx = (1/(e^(x^2)+1)) * (e^(x^2) * 2x)
Next, we will differentiate e*sin(x). The derivative of e*sin(x) is found by applying the product rule. The derivative of e is e, and the derivative of sin(x) is cos(x). Applying the product rule, we have:
d[e*sin(x)]/dx = e*cos(x) + e*sin(x) * 0 = e*cos(x)
Now, adding the derivatives of both terms, we get:
dy/dx = (1/(e^(x^2)+1)) * (e^(x^2) * 2x) + e*cos(x)
This is the derivative of the given function y with respect to x.
Learn more about derivative here :-
https://brainly.com/question/30365299
#SPJ11
A substance is tested and has a ph of 7.0. how would you classify it? a. a strong acid b. a strong base c. a weak acid d. neutral
Answers
A substance is tested and has a Ph of 7.0. It would be a weak acid.
The correct option is (c) a weak acid .
What is the nature of substance if the pH is less than 7?
Acidity is defined as pH below 7. More than 7 pH is considered basic. Each whole pH number below 7 is ten times more acidic than the next higher value since the pH scale is logarithmic. For instance, pH 4 is 100 times (10 times 10) more acidic than pH 6, while pH 5 is ten times (10 times) more acidic than pH 4.What is pH?
The pH scale determines how acidic or basic water is. The range is 0 to 14, with 7 representing neutrality. Acidity is indicated by pH values below 7, whereas baseness is shown by pH values above 7. In reality, pH is a measurement of the proportion of free hydrogen and hydroxyl ions in water.Learn more about pH
brainly.com/question/27945512
#SPJ4
Every winter, your family sets up a hot chocolate stand near the local ice skating rink. You sell cups of hot chocolate for $1.50 each, and you usually ...
Answers
During the winter season, a family sets up a hot chocolate stand near a local ice skating rink. They sell cups of hot chocolate for $1.50 each and typically sell 50 cups per day.
However, due to changes in weather conditions and customer preferences, the family decides to conduct a market experiment by varying the price of hot chocolate to assess the impact on sales volume. The experiment involves increasing the price to $2.00 per cup and monitoring the resulting sales.
By increasing the price of hot chocolate from $1.50 to $2.00 per cup, the family aims to observe how the change in price affects the demand for their product. The experiment helps them understand the price elasticity of demand, which measures the responsiveness of quantity demanded to changes in price. If the increase in price leads to a significant decrease in sales volume, it suggests that the demand for hot chocolate is elastic, meaning consumers are sensitive to price changes. Conversely, if sales remain relatively stable despite the price increase, it indicates that the demand is inelastic, indicating that consumers are less sensitive to price changes. The family can analyze the results of this experiment to make informed pricing decisions and optimize their profitability during the winter season.
To learn more about profitability: -
brainly.com/question/29662354
#SPJ11
Please help me with this question!!!!!

Answers
h = 11.9 cm
cos = adjacent/ hypotenuse
therefore:
cos(24) = h/ 13
rearrange:
h = 13cos(24)
put into calculator:
h = 11.8760...
rounded to one decimal point:
h = 11.9cm
Let A be an n×n matrix. Determine whether the statement below is true or false. Justify the answer. If λ+5 is a factor of the characteristic polynomial of A, then 5 is an eigenvalue of A. Choose the correct answer below. A. The statement is false. If λ+5 is a factor of the characteristic polynomial of A, then −5 is an eigenvalue of A. In order for 5 to be an eigenvalue of A, the characteristic polynomial would need to have a factor of λ−5. B. The statement is true. If λ+5 is a factor of the characteristic polynomial of A, then λ+5 must be an entry on the main diagonal of A−λI. C. The statement is true. If λ+5 is a factor of the characteristic polynomial of A, then λ=5 is a root of the characteristic equation. D. The statement is false. The factors of the characteristic polynomial are useful for determining the eigenvectors of a matrix, not its eigenvalues.
Answers
The correct answer is A. The statement is false. If λ+5 is a factor of the characteristic polynomial of A, then −5 is an eigenvalue of A. In order for 5 to be an eigenvalue of A, the characteristic polynomial would need to have a factor of λ−5. This is because the eigenvalues of a matrix A are the roots of its characteristic polynomial, which is given by det(A-λI) where I is the identity matrix.
If λ+5 is a factor of the characteristic polynomial, then det(A-(λ+5)I)=0. This implies that A has an eigenvector corresponding to eigenvalue -(λ+5), which is -5 in this case. Therefore, 5 is not necessarily an eigenvalue of A. Moreover, the diagonal of A-λI contains the eigenvalues of A, not λ+5 as mentioned in option B. Option C is also incorrect because having λ+5 as a factor of the characteristic polynomial does not necessarily mean that λ=5 is a root of the polynomial. Option D is also incorrect because the factors of the characteristic polynomial are used to determine both the eigenvalues and eigenvectors of a matrix.
To learn more about eigenvalues click here : brainly.com/question/14415841
#SPJ11
The statement is false. If λ+5 is a factor of the characteristic polynomial of A, then it means that λ=-5 is an eigenvalue of A, not 5. This is because the characteristic polynomial is defined as det(A-λI), where I is the identity matrix and det is the determinant function. Setting λ+5 as a factor means that det(A-(-5)I) = 0, which implies that -5 is an eigenvalue of A.
Therefore, in order for 5 to be an eigenvalue of A, the characteristic polynomial would need to have a factor of λ-5, not λ+5. It is also important to note that while the characteristic polynomial is useful for determining both the eigenvalues and eigenvectors of a matrix, the factors of the polynomial only determine the eigenvalues, not the eigenvectors.
To learn more about eigenvalue click here : brainly.com/question/14415841
#SPJ11
find surface area of the prism

Answers
Which function describes this table of values

Answers
Answer:
graphical method
of simultaneously linear equation
Find square root of 3420 by long division method correct up to 2 decimal places.
Answers
Answer:
58.480766068854
Step-by-step explanation:
hope it will help you
Suppose that s is the position function of an object, given as s(t) = 2t - 7. We compute the instantaneous velocity of the object at t = 6 as follows. Use exact values. First we compute and simplify (6 +h). s(6 + h) = Then we compute and simplify the average velocity of the object between t = 6 and t = 6 + h. 8(6+h) - s(6) h = Rationalize the numerator in the average velocity. (If it applies, simplify again.) $(6 + h) - $(6) h The instantaneous velocity of the object att = 6 is the limit of the average velocity as h approaches zero. s(6 + h) – $(6) v(6) lim h -0
Answers
The instantaneous velocity of the object at t = 6 is 2.
Suppose that s is the position function of an object, given as s(t) = 2t - 7. We compute the instantaneous velocity of the object at t = 6 as follows. Use exact values. First we compute and simplify (6 + h). s(6 + h) = 2(6 + h) - 7 = 12 + 2h - 7 = 2h + 5Then we compute and simplify the average velocity of the object between t = 6 and t = 6 + h.8(6+h) - s(6) h = 8(6 + h) - (2(6) - 7) h= 8h + 56
Then, to rationalize the numerator in the average velocity. (If it applies, simplify again.)$(6 + h) - $(6) h(h(h) + 56)/(h(h)) = (8h + 56)/h The instantaneous velocity of the object att = 6 is the limit of the average velocity as h approaches zero.s(6 + h) – $(6) v(6) lim h -0s(6 + h) – s(6) v(6) lim h -0Using the above calculation, we get:s(6 + h) – s(6) / h lim h -0s(6 + h) = 2(6 + h) - 7 = 2h + 5So,s(6 + h) – s(6) / h lim h -0(2h + 5 - (2(6) - 7)) / h= (2h + 5 - 5) / h = (2h / h) = 2
Therefore, the instantaneous velocity of the object at t = 6 is 2.
Learn more about Instantaneous velocity
brainly.com/question/28837697
#SPJ11
determine whether the series is convergent or divergent.
sigma^infinity _n = 0 ln(n^2+3/8n^2+7)
convergent divergent
if it is convergent, find its sum. (if the quantity diverges, enter diverges.)
Answers
To determine whether the series is convergent or divergent, we can use the integral test.
First, we note that the function f(x) = ln(x^2+3/8x^2+7) is continuous, positive, and decreasing for x ≥ 1.
Then, we take the integral of f(x) from 1 to infinity:
∫_1^∞ ln(x^2+3/8x^2+7) dx
We can evaluate this integral using integration by parts:
u = ln(x^2+3/8x^2+7) dv = dx
du/dx = (2x)/(x^2+3/8x^2+7) v = x
∫_1^∞ ln(x^2+3/8x^2+7) dx = [xln(x^2+3/8x^2+7)]_1^∞ - ∫_1^∞ (2x)/(x^2+3/8x^2+7) dx
We know that the limit of xln(x^2+3/8x^2+7) as x approaches infinity is infinity, so the first term evaluates to infinity.
For the second term, we can use the substitution u = x^2 to get:
∫_1^∞ (2x)/(x^2+3/8x^2+7) dx = ∫_1^∞ (2du)/(u+3/8u+7)
We can then use partial fractions to write the integrand as:
(2du)/((u/8)+7/8) - (2du)/(u+7)
We can now evaluate the integral:
∫_1^∞ (2du)/(u+3/8u+7) = [2ln(u/8+7/8)]_1^∞ = 2ln(∞/8+7/8) - 2ln(1/8+7/8) = ∞
∫_1^∞ (2du)/(u+7) = 2ln(u+7)]_1^∞ = ∞ - 2ln(8) = ∞
Since both integrals diverge, the original series diverges by the integral test. Therefore, the answer is divergent.
Know more about convergent here:
https://brainly.com/question/15415793
#SPJ11