Choose the number of solutions for the equation.9m - 3 - 5m = 3 + 4m - 6
Answers
Given:
The equation is 9m - 3 - 5m = 3 + 4m - 6.
The objective is to find the number of solutions fo the equation.
Explanation:
The equation can be solved as,
\(\begin{gathered} 9m-3-5m=3+4m-6 \\ 9m-5m-4m=3-6+3 \\ 9m-9m=-3+3_{} \\ 0=0 \end{gathered}\)Thus, the obtained answer is zero.
Hence, the equation has no solution.
Related Questions
The maximum speed that an X43A plane can reach is 7,500 miles per hour. At this speed, how many feet
can the X43A travel in 1 second? (1 mile = 5,280 feet)
Answers
Answer:
11000 feet/secondsStep-by-step explanation:
This problem requires that we convert from miles per hour to feet per seconds
Given that the speed of the X43A plane is 7500 mph
and that 1 mile = 5,280 feet)
\(=\frac{7500miles}{h} *\frac{5280 feet}{mile} \frac{1hour}{3600 seconds} \\\\=\frac{7500*5280}{3600} \\\\=\frac{396*10^5}{3600} \\\\=11000 feet/seconds\\\\=11*10^3feet/seconds\\\\\)
Therefore the speed of the X43A plane in feet per second is 11000
Jared lost a total of $56.00 on his investment over 7 months. He lost an equal amount of money each month. Jared used this equation to figure out how much money he lost each money. -56.00/7=-8.00 what does -56.00/7=-8.00 tell us?
Answers
Answer:
I'm not so very sure but I really need points
Multiplying and dividing ratio numbers
Answers
Answer:
with multiplying and dividing ratios you will need to either dividing or multiplying each of the terms in the ratios by the same number.
Step-by-step explanation:
Examples
12:14
you would divide by 2 and you would get
6:7
hope this helps
x+4=−14 x= ........................................................................
Answers
Answer: -18
Step-by-step explanation:
Triangle JKL has vertices at J(−1, −5), K(−2, −2), and L(2, −4). Determine the translation direction and number of units of the image of triangle JKL if vertex J′ is at (−3, −5).
4 units down
4 units up
2 units to the right
2 units to the left
Answers
A triangle JKL has vertices at J(−1, −5), K(−2, −2), and L(2, −4) and J′ at (−3, −5). The translation direction is 2 units to the left. The number of units of the image of triangle JKL is 2 units to the left only.
Given that a triangle JKL has vertices at J(−1, −5), K(−2, −2), and L(2, −4) and J′ at (−3, −5). We have to determine the translation direction and the number of units of the image of triangle JKL. Let's first find the translation direction to determine the image of triangle JKL.
Seeing the position of J and J', we can determine that the translation was made in the left direction because J has moved from the point (-1,-5) to (-3,-5). Thus, the translation direction is 2 units to the left. Now, let's calculate the number of units of the image of triangle JKL.
Let's draw a rough sketch of the triangle JKL and locate its vertices J(-1,-5), K(-2,-2), and L(2,-4).To find the number of units of the image of triangle JKL, we need to find the horizontal and vertical distances between the vertices of the original triangle and its image.
We can use the horizontal distance between J and J′ as a reference to calculate the remaining distances. J has moved 2 units to the left, so the horizontal distance between J and J′ is 2. Now, let's calculate the vertical distance between J and J′. The coordinates of J and J′ are (-1,-5) and (-3,-5), respectively.
The difference between the y-coordinates of J and J′ is 0, which means that J and J′ are on the same horizontal line. Therefore, the vertical distance between J and J′ is 0. Hence, the image of the triangle JKL has moved 2 units to the left and 0 units vertically. Thus, the number of units of the image of triangle JKL is 2 units to the left only.
For more questions on the triangle
https://brainly.com/question/17335144
#SPJ8
joey drew the following trapezoid Which group of ordered pairs represents the vertices of the trapezoid?
Answers
Answer:
a 2,3 2,5 4,5 7,9
Step-by-step explanation:
D. 12:28
es 22. The label on a box of cereal states that it
contains 6 servings. If there are 7.5 cups in
the box, how many cups of cereal are there
per serving?
Answers
pls help me on these 2 questions !!

Answers
Answer:
1. 23
2. 8
Step-by-step explanation:
☆Cross multiply.
\( \frac{2}{10} = \frac{4}{a - 3} \\ \\ 40 = 2(a - 3) \\ 40 = 2a - 6 \\ \frac{ + 6 = \: \: \: \: \: \: \: \: + 6}{ \frac{46}{2} = \frac{2a}{2} } \\ \\ 23 = a\)
--------
\( \frac{k}{6} = \frac{4}{3} \\ \\ \frac{24}{ 3} = \frac{3k}{3} \\ \\ 8 = k\)
. The length of the long-distance calls made by the employees of a company followed a normal distribution with a mean of 6.5 minutes and a standard deviation of 2 minutes. a. What is the probability that a call lasts less than 4 minutes
Answers
Answer:
The probability that a call lasts less than 4 minutes
P(X<4) = P(Z<-1.25) = 0.1056
Step-by-step explanation:
Step(i):-
Given mean of the population = 6.5 minutes
Given standard deviation of the Population = 2 minutes
Let 'X' be the random variable in normal distribution
Given X = 4
\(Z= \frac{x-mean}{S.D} = \frac{4-6.5}{2} = -1.25\)
Step(ii):-
The probability that a call lasts less than 4 minutes
P(X<4) = P(Z<-1.25)
= 1-P(z>1.25)
= 1 - ( 0.5 +A(1.25)
= 1-0.5 - A(1.25)
= 0.5 - 0.3944 ( from normal table)
= 0.1056
Final answer:-
The probability that a call lasts less than 4 minutes
P(X<4) = P(Z<-1.25) = 0.1056
plz help worth 50 points

Answers
Answer:
The answer is A
Step-by-step explanation:
Starting from -3 in the Y values of option A. If you subtract three from each value, you will get the next value to the right.
-3 minus -3 = -6-6 minus -6 = -9
Answer:
Someone already answered it but I won't let 50 points go to waste. !!!!!
Step-by-step explanation:
The ratio of the areas of two similar polygons can be found by using the ratio of their perimeters or the ratio of similarity and squaring it.
Answers
The ratio of the areas of two similar polygons can be found by using the ratio of their perimeters or the ratio of similarity and squaring it which is true.
What is a polygon?The polygon is a 2D geometry that has a finite number of sides. And all the sides of the polygon are straight lines connected to each other side by side.
Similar polygons are those whose perimeter ratios are identical to their respective scale factors. The common fraction of the sizes of two matching sides of two identical polygons is known as a scale factor.
The given statement is true.
More about the polygon link is given below.
https://brainly.com/question/17756657
#SPJ1
If a cube has volume 125cm³, find the height of the cube.
Answers
Answer:
height = 5 cm
Step-by-step explanation:
a cube has congruent sides (s)
the volume (V) of a cube is calculated as
V = s³
given V = 125 , then
s³ = 125 ( take cube root of both sides )
\(\sqrt[3]{s^3}\) = \(\sqrt[3]{125}\) = \(\sqrt[3]{5^3}\)
s = 5
then height = 5 cm
8) Two lines intersect as shown.
(2x + 20)
60°
What is the value of x?
A 20
B 40
C 50
D60

Answers
Answer:
A. 20
Step-by-step explanation:
Vertical angles are congruent, so ...
2x +20 = 60
x +10 = 30 . . . . . divide by 2
x = 20 . . . . . . . . .subtract 10
perimeter 254 meters and dimension measures 6 meters
Answers
Answer:
didn't even ask a question
Step-by-step explanation:
impossible to answer without a question
write an algebraic equation for the followingn problem and then solve for it. Hilltop dormitory just purchased a new soft drink machine on sale for $480. The sale price was 75% of the original price. What was the original price of the soft drink machine?
Answers
Answer:
Step-by-step explanation:480 x o.75=360
and now you add this amount on payed
360 + 480=840 was original price
A can contains 40 fluid Ounces of fruit juice. How many pints of fruit juice
does the can contain?
Answers
Answer:
2.5 pints of fruit juice
Answer:
2.5
Step-by-step explanation:
2(3x+10)=6x+20 does this equation have one solution or many ? Explain why
Answers
Answer:
2(3x+10) = 6x+20
6x+20 = 6x+20
6x = 6x
x = x
This has an infinite amount of solutions
Step-by-step explanation:
graph the line with slope -3/4 passing through the point (2,-1)
Answers
Answer:
Step-by-step explanation:
Slope of the line:
\(m = \frac{y-y1}{x-x1} \\\)
Given:
slope = -3/4
point (x1,y1) = (2, -1)
Substitute and solve
\(m = \frac{y-y1}{x-x1} \\-\frac{3}{4} = \frac{y-(-1))}{x-2} \\-3(x-2) = 4(y+1)\\-3x + 6 = 4y + 4 \\Transpose\\4y = -3x + 6 - 4\\4y = -3x + 2 \\y = -3/4x + 2/4\\y = -3/4x + 1/2\\OR\\4y +3x - 2 = 0\)
1/2 is the y-intercept
(0,1/2)
Since we have 2 points already, we can then graph the line.
(2, -1) and (0, 1/2)

find the inverse of each function

Answers
Answer:
c
Step-by-step explanation:
assume base 10
-logy = x
\( \frac{1}{ log(y) } = x\)
log base x y = 5 turns into the format x^ 5 = y
implement that to get c
please help me asapppppp

Answers
Answer:
T1=-12
T2=-19
T3=-26
Step-by-step explanation:
Determine which term will have a value of -6998
-7n-5=-6998
-7n=-6998+5
-7n=-6993
-7n/-7=-6993/-7
n=999
Simplifly the expression: x-3x-(-5x)
Answers
Answer:
The answer is 3x.
Step-by-step explanation:
I used a calculator
a local newspaper assigns a rating between 1 and 10 to every book and movie it reviews. Victor gathered data about five titles where the newspaper reviewed both the book and the movie version of the title. The ratings assigned by the newspaper are given in the table. Select the points that represent this data.


Answers
The points that represent this data are shown in the image attached below.
What is a scatter plot?A scatter plot is a type of graph which is used for the graphical representation of the values of two variables, with the resulting points showing any association (correlation) between the data set.
Based on the information provided in table above, the points that represent this data are shown in the image attached below.
Read more on scatterplot here: brainly.com/question/6592115
#SPJ1

Answer:
please look at the picture

3) After measuring the heights of 7 people, they have an average height of 156cm. After
measuring the heights of 8 people they have an average height of 158cm. How tall is
the 8th person?
Answer greatly appreciated asap
Answers
Answer:
172 cm
Step-by-step explanation:
The total height of the first 7 people is the average of the 7 people multiplied by the number of people, which is 156 * 7 or 1092. Using the same method, the total height of the first 8 people is 158*8 or 1264. The eighth person must be 1264 - 1092 cm tall or 172 cm tall.
Given the following model
Y=C+I0+g0
C=a+b (y-t)
t=d+ty
(a>0, 0 0, 0< t <1) t: income taxes
a) How many endogenous variables are there?
b) Find Y, C, and T
Answers
Answer:
Step-by-step explanation:
a) To determine the endogenous variables, we need to identify the variables that are determined within the model equation. In the given model, the endogenous variable is Y (output or national income).
b) Let's find Y, C, and T step-by-step:
Start with the equation Y = C + I0 + g0.
Substitute C from the equation C = a + b(y - T).
Y = (a + b(y - T)) + I0 + g0.
Substitute T from the equation T = d + tY.
Y = (a + b(y - (d + tY))) + I0 + g0.
Expand the equation:
Y = a + by - bd - btY + I0 + g0.
Rearrange the equation to isolate Y:
Y + btY = a + by - bd + I0 + g0.
Y(1 + bt) = a + by - bd + I0 + g0.
Y = (a + by - bd + I0 + g0) / (1 + bt).
Now, Y is expressed in terms of the exogenous variables a, b, d, I0, g0, and the endogenous variable Y itself, along with the parameter t.
To find C and T, we can substitute the obtained Y value back into the respective equations:
Substitute Y into the equation C = a + b(y - T):
C = a + b(y - T) = a + b(y - (d + tY)) = a + by - bd - btY.
C = a + by - bd - bt[(a + by - bd + I0 + g0) / (1 + bt)].
Now, C is expressed in terms of the exogenous variables a, b, d, I0, g0, and the endogenous variable Y, along with the parameter t.
Substitute Y into the equation T = d + tY:
T = d + tY = d + t[(a + by - bd + I0 + g0) / (1 + bt)].
Now, T is expressed in terms of the exogenous variables d, t, and the endogenous variable Y, along with the parameters a, b, I0, and g0.
It's important to note that in the given model, there is only one endogenous variable, Y (national income/output). C and T are determined based on the values of Y and the exogenous variables.
What is the prime factorization of 156?
Answers
This is the answer :)
Find the value of x.
x = ___

Answers
Solving steps In photo wrote down on paper

SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
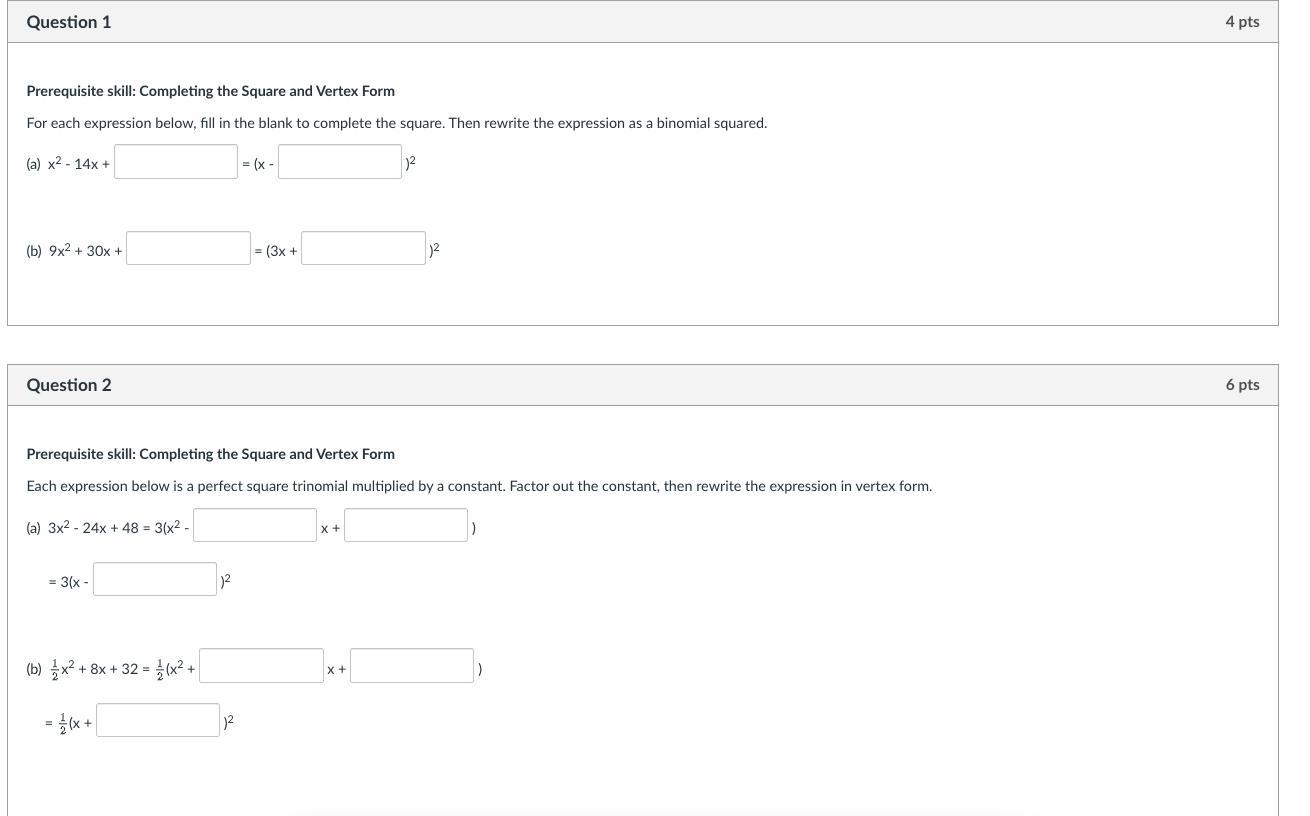
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
One rectangle is divided into 4 parts how much is one part
Answers
Thank you!
This question is unanswerable unless the answer is 1/4 rectangle.
Three ferry services A, B, and C leave from the same jetty at different intervals.
Services A, B, and C leave the jetty once every 10 minutes, 12 minutes and 15 minutes
respectively. Given that the first ferry of the three services left the jetty together at
09 00 on a particular day, find
(a) the earliest time that the 3 ferry services next leave the jetty together again.
(b) the earliest time Amy will leave the jetty given that Amy reached the jetty on
this particular day at 09 30 and takes the ferry service B from the jetty.
(c) the time of the last ferry of Service A to leave the jetty on this particular day,
given that the jetty closes at 23 25.
Answers
b) 9:24
c)23:20
If m∠1 ≅ 115°, find m∠6
Answers
Answer:
Therefore, m∠6 is 115 degrees and m∠2 is 50 degrees.
Step-by-step explanation:
To find m∠6, we need to use the fact that the sum of the measures of the angles in a triangle is 180 degrees.
From the given information, we know that m∠1 is 115 degrees. We also know that ∠1 and ∠6 are vertical angles, which means they are congruent. Therefore, m∠6 is also 115 degrees.
Now, we can use the fact that angles ∠1, ∠2, and ∠6 form a triangle to find the measure of ∠2.
The sum of the measures of the angles in a triangle is 180 degrees, so:
m∠1 + m∠2 + m∠6 = 180
Substituting the known values, we get:
115 + m∠2 + 115 = 180
Simplifying, we get:
m∠2 = 180 - 115 - 115
m∠2 = 50
Therefore, m∠6 is 115 degrees and m∠2 is 50 degrees.