Answers
Check the picture below.

Answer:
The correct answer is d.
Step-by-step explanation:
On Acellus
have a great day!
:)
Related Questions
how to solve the first order linear differential equation
Answers
The solution to the given differential equation is y = e⁽ˣ³⁾⁽²⁸ˣ ⁺ ᶜ⁾, where C is a constant.
To solve the first-order linear differential equation of the form y' + p(x)y = q(x), where p(x) and q(x) are functions of x:
Find the integrating factor (IF) = e⁽∫ᵖ⁽ˣ⁾ᵈˣ⁾
Multiply both sides of the equation by the IF.
Apply the product rule to the left side and simplify the right side.
Integrate both sides with respect to x.
Solve for y.
Using this method, for the given equation:
y' - 3x²y = 28e⁽ˣ³⁾
Find the integrating factor (IF):
IF = e⁽∫ᵖ⁽ˣ⁾ᵈˣ⁾ = e⁽⁻³/¹ * ∫ˣ²ᵈˣ⁾ = e⁽⁻ˣ³⁾
Multiply both sides by the IF:
e⁽⁻ˣ³⁾y' - 3x²e⁽⁻ˣ³⁾y = 28
Apply the product rule to the left side and simplify the right side:
d/dx (e⁽⁻ˣ³⁾y) = 28
Integrate both sides with respect to x:
e⁽⁻ˣ³⁾)y = 28x + C, where C is the constant of integration.
Solve for y:
y = e⁽ˣ³⁾(28x + C)
Therefore, the solution to the given differential equation is y = e⁽ˣ³⁾(28x + C), where C is a constant.
Learn more about linear equation here: brainly.com/question/12423682
#SPJ4
Complete question:
How to solve the first order linear differential equation
Y'- 3x²y=28eˣ³
The freight truck has the length of 40 feet, width of 20 feet and height of 15 feet? What is the total volume of the truck? Plz help me!!

Answers
if `\frac{3}{4}` pound of nails fills a container `\frac{2}{3}` full, then how many pounds of nails will fill the container?
Answers
Let's use the proportion method to solve the problem. We know that \frac{3}{4} pound of nails fills \frac{2}{3} of the container. Let x be the total weight of nails that will fill the container. Then we can set up the proportion:
\frac{3}{4} / \frac{2}{3} = x / 1
To solve for x, we can cross-multiply and simplify:
\frac{3}{4} * \frac{3}{2} = x
x = \frac{9}{8} = 1.125 pounds of nails
Therefore, 1.125 pounds of nails will fill the container.
Learn more about Fraction here:- brainly.com/question/78672
#SPJ11
Determine the intercepts of the line.
Do not round your answers.
3x + 2y = 5
Y=0
X=0
Answers
Answer:
Step-by-step explanation:
X axis intercept (y=0)
3x+2(0)=5
3x=5
x=5/3
Y axis intercept (x=0)
3(0)+2y=5
2y=5
y=5/2
so, the interception points are: (5/3,0) and (5/2,0)
Theorem 22.8 If R is a ring with additive identity 0, then for any a, b E R we have 1. 0aa0 = 0, 2. a(-b)= (-a)b = -(ab), 3. (-a)(-b) = ab
Answers
Theorem 22.8 states several properties of rings with additive identity 0. These properties involve the multiplication and negation of elements in the ring.
Specifically, the theorem asserts that the product of any element with the additive identity is zero, the product of an element with its negative is the negation of the product with the positive element, and the product of two negatives is equal to the product of the corresponding positive elements.
Theorem 22.8 provides three key properties of rings with additive identity 0:
0aa0 = 0:
This property states that the product of any element a with the additive identity 0 is always 0.
In other words, multiplying any element by 0 results in the additive identity.
a(-b) = (-a)b = -(ab):
This property demonstrates the relationship between the negation and multiplication in a ring.
It states that the product of an element a with its negative -b is equal to the negation of the product of a with the positive element b.
This property highlights the distributive property of multiplication over addition in a ring.
(-a)(-b) = ab:
This property shows that the product of two negatives, -a and -b, is equal to the product of the corresponding positive elements a and b. It implies that multiplying two negatives yields a positive result.
These properties are fundamental in ring theory and provide important algebraic relationships within rings.
They help establish the structure and behavior of rings with respect to multiplication and negation.
To learn more about additive identity visit:
brainly.com/question/23172909
#SPJ11
graph equation y-5=-5(x-1)
Answers
Answer:
your slope intercept form is y=-5x+6
Step-by-step explanation:
you distribute the -5 and then you add 5 to your now positive 5 to isolate your y variable
then once you have the equation you start at your y-intercept (0,6) and then you go up and or down 5 then you move to the left one because you have a negative slope
Let's assume the average speed of a serve in women's tennis is around 118 mph, with a standard deviation of 12 mph. We recruit 100 amateur tennis players to use our method this time, and after 6 months we calculate a group mean of 123 mph.
Reference: 8.54 More about confidence intervals, effect sizes, and tennis serves
a. Based on the 95% confidence interval computed in #5, which statement best reflects the findings. (Read each option carefully)
A. Because the population mean of 118 mph falls within the confidence interval around the new mean, we can not conclude that the program had an impact. We do not have evidence to support that it changed the speed of a tennis serve.
B. Because the population mean of 118 mph does not fall within the confidence interval around the new mean, we can not conclude that the program had an impact. We do not have evidence to support that it changed the speed of a tennis serve.
C. Because the population mean of 118 mph falls within the confidence interval around the new mean, we can conclude that the program had an impact. In fact, we can conclude that the program seemed to increase the average speed of women’s serves.
D. Because the population mean of 118 mph does not fall within the confidence interval around the new mean, we can conclude that the program had an impact. In fact, we can conclude that the program seemed to increase the average speed of women’s serves.
Answers
The correct answer is (D) Because the population mean of 118 mph does not fall within the confidence interval around the new mean, we can conclude that the program had an impact. In fact, we can conclude that the program seemed to increase the average speed of women’s serves.
Because the population mean of 118 mph does not fall within the confidence interval around the new mean, we can conclude that the program had an impact. In fact, we can conclude that the program seemed to increase the average speed of women’s serves.
The confidence interval around the group mean of 123 mph suggests that the true population mean lies somewhere within a certain range. Since the lower limit of this range is above the population mean of 118 mph, we can infer that the program had a positive impact on the participants' average serve speed.
This suggests that the program was successful in improving the participants' skills and abilities in tennis, resulting in faster serves.
To know more about confidence interval, refer the link:
https://brainly.com/question/24131141#
#SPJ11
what does it mean to say that an allele is "fixed"?
Answers
Answer:
When we say that an allele is "fixed," it means that a particular allele has reached a frequency of 100% in a population.
Step-by-step explanation:
Alleles are different forms of a gene that occupy the same position on homologous chromosomes. In a population, different alleles can exist for a specific gene. However, through various evolutionary processes such as natural selection, genetic drift, or gene flow, one allele may become predominant and eventually fixate within the population.
The fixation of an allele can occur through different mechanisms. For example, if a beneficial allele provides a selective advantage to individuals carrying it, it is more likely to increase in frequency and eventually become fixed in the population. On the other hand, genetic drift, which is the random change in allele frequencies due to chance events, can also lead to the fixation of an allele, especially in small populations.
Once an allele is fixed in a population, it means that all future generations will inherit that allele, and no alternative alleles will be present at that particular gene locus.
Learn more about allele here, https://brainly.com/question/3452155
#SPJ11
a ___ equation is an equation that contains a variable within a radical expression.
Answers
A radical equation is an equation that contains a variable within a radical expression.
To know more about radical equation refer here:
https://brainly.com/question/9370639
#SPJ11
Need Help With This ASAP

Answers
Express x2-5x + 8 in the form (x-a)² + b
where a and b are top-heavy fractions.
Answers
Using Complete the Square method, we find out that \(x^{2} -5x+8\) can be expressed in the form of \((x-a)^{2}+b\) as \((x-\frac{5}{2}) ^{2} +\frac{7}{4}\) where a and b are top-heavy fractions.
It is given to us that the expression is -
\(x^{2} -5x+8\) ----(1)
We have to express it in the form of\((x-a)^{2}+b\) where a and b are top-heavy fractions.
In order to achieve the required expression in the form of \((x-a)^{2}+b\) we have to use "Completing the Square" method.
The given expression from (1) is -
\(x^{2} -5x+8\)
This expression is in the form of \(ax^{2} +bx+c\)
Adding and subtracting \((b/2)^{2}\) terms into the expression, we get
\(x^{2} -5x+[\frac{5}{2}] ^{2}-[\frac{5}{2}] ^{2}+8\) -----(2)
Equation (2) can also be represented as -
\((x-\frac{5}{2}) ^{2} -[\frac{5}{2}] ^{2} +8\)
\(= > (x-\frac{5}{2}) ^{2} -\frac{25}{4} +8\\= > (x-\frac{5}{2}) ^{2} +\frac{7}{4}\)------- (3)
We see that equation (3) is in the form of \((x-a)^{2}+b\).
So, we can derive that -
\(a=\frac{5}{2}\)
and, \(b=\frac{7}{4}\).
Thus, \(x^{2} -5x+8\) can be expressed in the form of \((x-a)^{2}+b\) through "Complete the Square" method as \((x-\frac{5}{2}) ^{2} +\frac{7}{4}\) where a and b are top-heavy fractions.
To learn more about complete the square method visit https://brainly.com/question/4822356
#SPJ9
Ms. Lee works at a pizzeria. She delivers an average of 3 pizza orders per hour. The pizzeria is offering a bonus to employees who complete 200 deliveries or more in a month. She has delivered 26 orders so far this month. How many more hours, x, does Ms. Lee need to work to get the bonus?
Answers
Answer:
58 hours.
Which can also be 2days 10 hours.
Step-by-step explanation:
3 pizza orders = 1hour
200 deliveries per month= bonus
26 orders so far this month.
X= 200-26= 174
174 divided by 3 = 58 hours.
Consider a function f(x,y,z)=a∗x^3 + b∗2y^2 + c∗z. Write a method to compute the value of such a function, given a,b,c,x,y, and z. The method should have the signature double compute (double a, double b, double c, double x, double y, double z ). Feel free to write this method in an IDE. Do not call other methods such as Math. pow from within your code. How much space (in terms of the size of double values) does the JYM lay out on the stack when this method is invoked? In other words, space for how many double s must be set aside when this method is invoked to hold the parameters, any necessary local variables, and the return value? Only consider method arguments, local variables, and return values for this method, and not any others your code may call.
Answers
A truth table is a table used in logic to systematically represent the possible truth values of a logical expression.
To construct truth tables for the provided statement forms, we need to consider all possible combinations of truth values for the individual propositional variables involved.
Let's go through each statement form and build the respective truth tables:
(a) p∧∼q:
p q ∼q p∧∼q
T T F F
T F T T
F T F F
F F T F
(b) ∼(p∧q)∨(p∨q):
p q p∧q ∼(p∧q) p∨q ∼(p∧q)∨(p∨q)
T T T F T T
T F F T T T
F T F T T T
F F F T F T
(c) p∧(q∧r):
p q r q∧r p∧(q∧r)
T T T T T
T T F F F
T F T F F
T F F F F
F T T T F
F T F F F
F F T F F
F F F F F
(d) p∧(∼q∨r):
p q r ∼q ∼q∨r p∧(∼q∨r)
T T T F T T
T T F F F F
T F T T T T
T F F T T T
F T T F T F
F T F F F F
F F T T T F
F F F T T F
These truth tables display all the possible combinations of truth values for the propositional variables p, q, and r, and the resulting truth values for each statement form based on the logical operations involved.
To know more about truth table refer here:
https://brainly.com/question/30588184#
#SPJ11
What are the zeros oh g(x)=x(x+1)(x-2)^2
Answers
\(~~~~~x(x+1)(x-2)^2 =0\\\\\implies x = 0~~ \text{or}~~ x +1 = 0~~ \text{or}~~ (x-2)^2 = 0\\\\\implies x = 0, ~ x = -1 , ~x=2\\\\\text{Hence the roots are}~0,-1 ,~2\)
Lashawn used 44 stamps to mail a package. He used a
combination of $0.50 stamps, $0.35 stamps, $0.02 stamps,
totaling $15.01. If the number of $0.35 stamps is nine less
than twice the number of $0.50 stamps, find the number of
each type of stamp.
Answers
Answer:
Lashawn used 15, $0.50 stamps, 21, $0.35 stamps, and 8, $0.02 stamps to mail the package
Step-by-step explanation:
The given parameters are;
The number of stamps Lashawn used to mail the small package = 44
The price of the combination of 44 stamp = $15.01
The price categories of the stamps are $0.50, $0.35, and $0.02
The number of $0.35 stamps = 2 × The number of $0.50 stamps - 9
Let, x represent the number of $0.50 stamps Lashawn used to mail the package
We have;
The number of $0.50 stamps Lashawn used to mail the package = x
The number of $0.35 stamps = 2 × x - 9 = 2·x - 9
The number of $0.35 stamps = 2·x - 9
The number of $0.02 stamps = 44 - x - (2·x - 9) = 44 - x - 2·x + 9 = 53 - 3·x
The number of $0.02 stamps = 53 - 3·x
Which gives;
0.5 × x + 0.35 × (2·x - 9) + 0.02 × (53 - 3·x) = 15.01
0.5·x + 0.7·x - 3.15 + 1.06 - 0.06·x = 15.01
1.14·x - 2.09 = 15.01
1.14·x = 15.01 + 2.09 = 17.1
x = 17.1/1.14 = 15
x = 15
The number of $0.50 stamps Lashawn used to mail the package = x = 15 stamps
The number of $0.50 stamps Lashawn used = 15 stamps
The number of $0.35 stamps Lashawn used = 2·x - 9 = 2 × 15 - 9 = 21 stamps
The number of $0.02 stamps Lashawn used = 53 - 3·x = 53 - 3 × 15 = 8 stamps.
What is the circumference of a circle with a radius of 11?
Answers
The circumference of a circle with a radius of 11 is 68.1
The route or boundary that encircles any shape in mathematics is defined by the shape's circumference. In other terms, the circumference is also known as the perimeter, which aids in determining how long a shape's outline is.
The formula to calculate the circumference of a circle is C=2\(\pi\)r where r is the radius of the circle.
The problem tells us that r= 11, substituting that in the equation and solving:
C=2\(\pi\)r =2\(\pi\)(11) = 22\(\pi\)
The value of \(\pi\) is approximately 3.14, putting the value of \(\pi\) in the equation:
C= 22(3.14) = 68.08→ 68.1
To learn more about the circumference of a circle visit:brainly.com/question/29142813
#SPJ4
Earth has a radius of 3959 miles. A pilot is flying at a steady altitude of 1.8 miles above the earth's surface.
What is the pilot's distance to the horizon
Enter your answer, rounded to the nearest tenth
Answers
That’s 3961miles as the final answer
Which type of triangle can be constructed with a 50° angle between two 8-inch sides? A. Equilateral B. Isosceles C. Scalene D. Obtuse.
Answers
The correct option is (C) Isosceles. An Isosceles triangle can be constructed with a 50° angle between two 8-inch sides.
This is because isosceles triangle having two sides that are equal in length, and have 50° angle, which is acute angle, that is less than 90°. This state that the remaining angle in the triangle must also be acute triangle, as the sum of all angles in a triangle must equal 180°.
This means that the remaining angle must be 80° (i.e. 180 - 50 = 80). An isosceles triangle is triangle consisting of two sides of equal length and two angles of equal measure. The two equal sides that make up the isosceles triangle are referred to as the base and the remaining side is height or altitude.
To know more about An Isosceles triangle:
brainly.com/question/29793403
#SPJ4
The temperature was 23° F at 8 A.M. By 1 P.M. the temperature was 13° F. Which of the following best represents the change in the temperature from 8 A.M. to 1 P.M.?

Answers
Answer:
G: -10 F
Step-by-step explanation: The temparature went down by 10 which means it subtracted 10 so it's -10
A reporter determines a baseball player's batting average, which is a ratio of number of hits to number of times at bat. The result is shown on a calculator as 0.2121
Answers
Complete question :
A reporter determines a baseball player's batting average, which is a ratio of number of hits to the number of times at bats. The result shown on a calculator as 0.2121....
How many hits would the player be expected to get in 200 at bats? Explain
Answer:
42
Step-by-step explanation:
Given that:
Batting average = number of hits / number of time at bats
Batting average obtained = 0.2121...
If at bats of the player = 200
Hence, number of hits ;
Batting average = number of hits / number of time at bats
0.2121 = number of hits / 200
Number of hits = 0.2121 * 200
Number of hits = 42.42..
= 42 ( approx)
C.Given the figure on the right. Answer the following.
Another Plzz

Answers
Answer:
10
Step-by-step explanation:
Remark
Technically, we can't. We have no way of knowing what kind of figure we are working with. We can say to you that if this is not at least a parallelogram then no answer is possible.
Opposite sides of a parallelogram are equal.
Equation
2x = x + 5
Solution
Subtract x from each side
2x - x = 5
x = 5
HE = 2x
HE = 2*5
HE = 10
can someone help me plss

Answers
Answer:
3 is vertical
1 is same side interior
2 is correspnding
4 is straight angles
Step-by-step explanation:
Write V-245 in simplest radical form.
Answers
\(\sqrt{-245}\implies \sqrt{(-1)(245)}\implies \sqrt{-1}\sqrt{245}\implies i\sqrt{49\cdot 5} \\\\\\ i\sqrt{7^2\cdot 5} \implies 7\sqrt{5}~i\)
I NEED AN ANSWER ASAP PLEASE

Answers
Step-by-step explanation:
the correct answer is option a 6a-7
Which numbers make a true statement when placed in the box? 5.067> □ Select each correct answer. 5.009 5.047 5.071 5.607
Answers
Answer: A, B
Step-by-step explanation:
Answer:
5.047 and 5.009
el gato?
Need help with these two problems
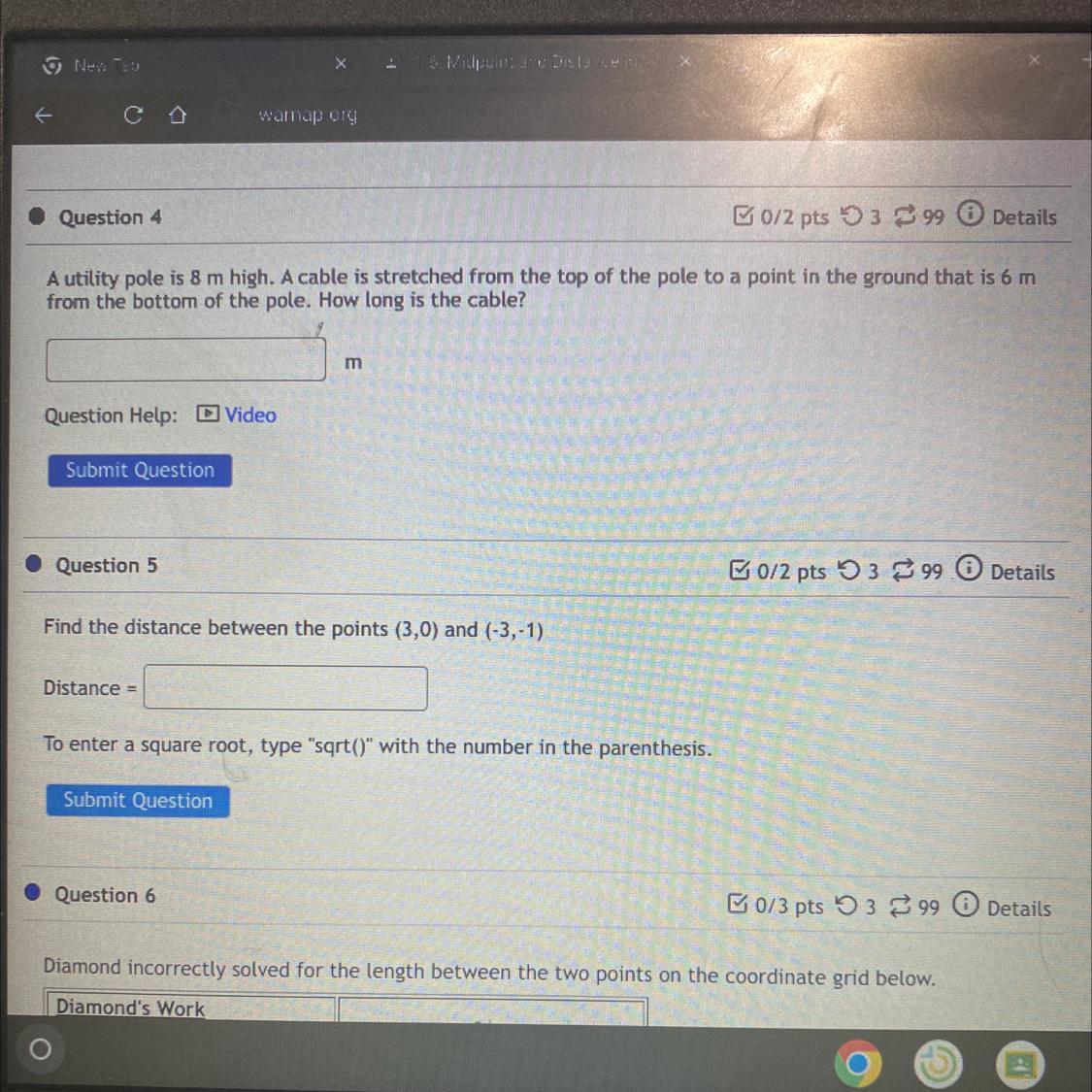
Answers
Answer:
Question 4 : 10 m
Question 5 : Square root 37
Step-by-step explanation:
QUESTION 4: So for the this one here we need to make a drawing (unfortunately). Lets break down the question because having a math problem with a ton of words is confusing sometimes. So we have a pole that is 8m high, so we can draw that out. So we take some cable and go 6 m from the bottom of the pole. So now we want to know how long the cable is and if we go from the top of the pole to the bottom 6m away it looks like this. (Below I'll put what I have written) Since now it's a 90 degrees angle there is a specific formula we can use in situations like this. Where we know 2 sides and need 1 more. a^2 + b^2 = c^2 should look familiar if it doesn't its all good! :D a^2 + b^2 = c^2 is called 'Pythagorean's theorem' (we don't really need to know that part) but basically we use it whenever we need to figure out a side when we already know the other two. We know that the straight line is 8, and the horizontal line is 6. So we can use that formula to get the last number. just know that whenever we have the right triangle, we can use the a^2 + b^2 = c^2 to get all the sides for it. The a and b in the formula are always the straight lines. The c is always the slanted line (the red line I drew). We don't know what it is, so we'll just put c^2 into our equation but we can solve for it! So 8^2 would equal to 64. 6^2 would equal to 36. 64 + 36 here gets us 100. Here's another trick you might need to memorize. Whenever there is a number squared like c^2, we can take the square root of both sides to get rid of it. So c^2 just becomes c. It's a little weird but very useful to remember. But if you remember the a^2 + b^2 = c^2 and use that square root technique you can get an A+ every time. :D Now all we need to know is the square root of 100. It's a big one so using a calculator is fine, here its just 10. Therefore our answer is 10.
QUESTION 5: We'll start off by reading 'distance between points' is a big thing to note here. There is a formula that we can directly use here. (I'll write under the picture in black). So distance between points always uses this formula: (In black). Okay, so the formula in black has more letters in it (which sucks) but we can break it down. When we have numbers like this (3, 0) it means (x, y). So I wrote down what the x1, y1, x2, y2, are here. X1 is just the first number, y1 is the second, x2 is the third, and y2 is the fourth. I just plugged in all the numbers from above in the order we put (x2, x1, y2, y1). Basically we can just solve this now! As of right now we'll need to solve (-3 -3)^2 when we solve that we should get 36. Next we're gonna solve (-1 - 0)^2 and we should get the answer of 1. Now we need to solve 36 +1 and we should know that it equals 37. Therefore we'd get answer: square root 37.


A square has an area of 20 square feet. What is the length of a side of the square, in feet?
Answers
Answer:
5
Step-by-step explanation:
There are 4 equal sides on a square so 20/4 which is 5.
Write the equation of a line in slope-intercept form, that passes through the point (6,-4) and its parallel to the line y=3x-8
y=
Answers
Answer:
Step-by-step explanation:
We'll look for a line with the form of y = mx + b, where m is the slope and b is the y-intercept (the value of y when x = 0).
A parallel line will have the same slope as the reference line, For y=3x-8, the slope is 3. We can write:
y =3x + b for the new line. We need a value of b that will cause the line to include point (6,-4). To find a b that will work, simple use the given point in the above equation and solve for b:
y =3x + b
-4 =3(6) + b for (6,-4)
-4 =18 + b
b = -22
The parallel line that goes through point (6,-4) is y = 3x - 22
See the attached graph.

Click on the measure of angle x

Answers
Answer:
142
Step-by-step explanation:
x+38=180
x=142
Answer is 142
Answer:
very easy x=180-38= 142 is ans
Step-by-step explanation:
itis Because the sum of all side in triangle is 180 so 180-38=x
if a is any integer, is a (a plus 1 )even or odd? say which it is (4 pts) and explain why (as a simple proof) (8 pts).
Answers
==================================================
Proof:
We'll break the proof into two cases which I'll label A and B
Case A: 'a' is evenCase B: 'a' is odd-----------
Case A: 'a' is even
k = some integer
a = 2k = some even integer
a+1 = 2k+1
a(a+1) = 2k(2k+1) = 2(2k^2+k) = 2*(some integer)
Since 2 is a factor of that last expression, this shows that a(a+1) is even when 'a' is even.
-----------
Case B: 'a' is odd
k = some integer
a = 2k+1 = some odd integer
a+1 = (2k+1)+1 = 2k+2
a(a+1) = (2k+1)(2k+2) = 2(2k+1)(k+1) = 2(some integer)
This shows that a(a+1) is even when 'a' is odd.
-----------
Therefore, for any integer 'a', the expression a(a+1) is always even.
Some examples:
a = 3, a+1 = 3+1 = 4, a(a+1) = 3*4 = 12 which is evena = 12, a+1 = 12+1 = 13, a(a+1) = 12*13 = 156 which is even-----------
Here's a slightly different way to interpret why the proof works.
a(a+1) consists of factors 'a' and 'a+1'
If 'a' was even, then a(a+1) is automatically even since 2 is a factor of 'a'.If 'a' was odd, then a+1 is even and we arrive at the same conclusion as before.Either way, we'll have 2 as a factor somewhere in a(a+1).
