Carson claims that the opposite of any integer is always a negative number.
Is he correct? Explain why or why not.
Answers
Related Questions
Let the random variables x and y have joint pdf as follows: f(x,y) = 1/5(11x^2 + 4y^2), 0 < x < 1,0 < y < 1 Find Cov(x,y) (round off to third decimal place). Find E(Y) (round off to third decimal place).Find E(XY) (write up to third decimal place).
Answers
Let the random variables x and y have joint pdf as follows: f(x,y) = 1/5(11x^2 + 4y^2) so Cov(x,y) (round off to third decimal place) is 0.241.
The covariance formula in statistics is used to evaluate the relationship between two variables. In essence, it serves as a gauge for the variation between two variables. Covariance is calculated by multiplying the units of the two variables, and it is expressed in units. Any positive or negative value might be the variance.
E[(X−EX)(Y−EY)]
=E[XY−X(EY)−(EX)Y+(EX)(EY)]
=E[XY]−(EX)(EY)−(EX)(EY)+(EX)(EY)
=E[XY]−(EX)(EY).
E(Y) = ∫ 1/x dx = ∫ 11/5 = ln 11/5 = 0.788
E(XY) = E[X 1/X]= 1
It is feasible to get the correlation coefficient formula from the covariance using the aforementioned formula, and vice versa. Units of covariance are calculated by multiplying the units of the two provided variables.
Learn more about Covariance:
https://brainly.com/question/28135424
#SPJ4
for each of the number lines, write an absolute value equation in the form |x-c|=d, where c and d are some numbers, to satisfy the given solution set.

Answers
An absolute value is the numerical value of a number without consideration of its sign. It can be represented graphically by a straight line known as a number line. Absolute value equations are equations that include absolute values of variables or unknown quantities. The following are examples of how to write an absolute value equation in the form |x-c|=d to fit the provided solution sets:
Example 1:
Solution set: {x|x≤-3 or x≥1}
Absolute value equation: |x-(-1)|=4
Explanation: -1 is the midpoint of the two ranges (-3 and 1) in the solution set. |x-(-1)|=|x+1| is the absolute value expression for the midpoint -1. The distance d from -1 to the solutions' furthest endpoints, 1 and -3, is four, hence the value of d in the absolute value equation is 4.
For such more question on equations
https://brainly.com/question/22688504
#SPJ11
The ages of each of the basketball players on a team are given.
13, 13, 13, 14, 14, 17, 18, 18
What is the mean age of these players?
Answers
Answer:
15
Step-by-step explanation:
We add up the ages of all the basketball players.
13 + 13 + 13 + 14 + 14 + 17 + 18 + 18 = 120
Now we divide by the number of basketball players.
120 ÷ 8 = 15
The mean age of the basketball players are 15.
Answer:
Mean = 15
Step-by-step explanation:
Mean = sum of observation. ÷ total no. of observation
= 13 + 13 + 13 + 14 + 14 + 17 + 18 + 18 ÷ 8= 120 ÷ 8= 15Question in picture solve for brainlist

Answers
Answer:
x=3
Step-by-step explanation:
Step 1: Simplify both sides of the equation.
14+5x=−5(x−8)+4
14+5x=(−5)(x)+(−5)(−8)+4(Distribute)
14+5x=−5x+40+4
5x+14=(−5x)+(40+4)(Combine Like Terms)
5x+14=−5x+44
5x+14=−5x+44
Step 2: Add 5x to both sides.
5x+14+5x=−5x+44+5x
10x+14=44
Step 3: Subtract 14 from both sides.
10x+14−14=44−14
10x=30
Step 4: Divide both sides by 10.
10x/10 = 30/10
Answer:
x=3
Step-by-step explanation:
1. Rearrange terms
2. Distribute
3. Add the numbers
4. Subtract14 from both sides of the equation
5. Simplify
Solve for x.
OA. 9
OB. 1
OC. 4
OD.7

Answers
The value of x in the secant intersection is 4.
How to find the length in a secant?If two secant segments are drawn to a circle from an exterior point, then the product of the measures of one secant segment and its external secant segment is equal to the product of the measures of the other secant segment and its external secant segment.
Therefore, let's find the value of x using the secant intersection theorem as follows;
4(4+x + 2) = 5(5 + x - 1)
4(6 + x) = 5(4 + x)
24 + 4x = 20 + 5x
24 - 20 = 5x - 4x
x = 4
Therefore,
x = 4
learn more on secant here: https://brainly.com/question/15601706
#SPJ1
How would I graph this?

Answers
Help meeeeeeeeee I need the answer
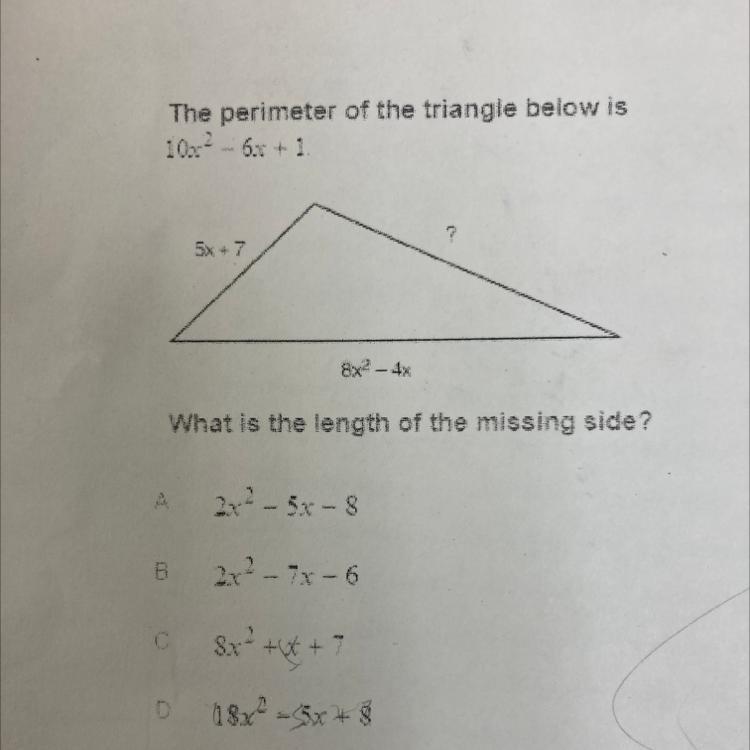
Answers
Answer:
d is the answer
Step-by-step explanation:
Answer:
B.
Step-by-step explanation:
\(?=(10x^{2} -6x+1)-(5x+7)-(8x^{2} -4x)\)
\(=10x^{2} -8x^{2} -6x-5x+4x+1-7\)
\(=2x^{2} -11x-4x-6\)
\(=2x^{2} -7x-6\)
Hope this helps
Using zero product property: (8b+1)(b+8)=0
Answers
Answer:
Step-by-step explanation:
8b + 1 = 0
8b = -1
b = -1/8
b + 8 = 0
b = -8
what is the probability of getting an A and then a 2?
Answers
Answer:
it would techically be a 50/50 chance of getting either an A or a 2
Brainliest and 20 points fully explain

Answers
Answer/Step-by-step explanation:
Part A
(x + 13) + (4x - 8) = 90
x + 13 + 4x - 8 = 90
5x + 5 = 90
-5 -5
-----------------
5x = 85
÷5 ÷5
--------------
x = 17
Part B
m∠OPQ = (x + 13)°
m∠OPQ = (17 + 13)°
m∠OPQ = 30°
m∠RPS = (4x - 8)
m∠RPS = (4(17) - 8)
m∠RPS = (68 - 8)
m∠RPS = 60°
Part C
Vertical angles equal each other. To test if they are vertical angles they would need to be equal to each other.
x + 13 = 4x - 8
-4x -4x
------------------------
-3x + 13 = -8
-13 -13
----------------------
-3x = -21
÷-3 ÷-3
-----------------
x = 7
x + 13 = 4x - 8
(7) + 13 = 4(7) - 8
20 = 28 - 8
20 = 20
These angles equal each other; therefore, they are also vertical angles.
----------------------------------------------------------------------------------------------------------
I hope this helps!
Who needs help with math?
I will help you
Answers
Answer:
MEEEEEEEEEEEEE I GOING POST IT RIGHT NOW
Step-by-step explanation:
can you help with calculus? with polynomial graphs and some kind of domain and some kind of derivative.
Is the event independent or overlapping:
A spinner has an equal chance of landing on each of its eight numbered regions. After spinning, what is the probability you land on region three and region six?
Mutually exclusive or independent:
A bag contains six yellow jerseys numbered 1-6. The bag also contains four purple jerseys numbered 1-4. You randomly pick a jersey. What is the probability it is purple or has a number greater than 5.
Mutually exclusive or overlapping:
A box of chocolates contains six milk chocolates and four dark chocolates. Two of the milk chocolates and three of the dark chocolates have peanuts inside. You randomly select and eat a chocolate. What is the probability that is is a milk chocolate or has no peanuts inside?
Mutually exclusive or independent:
You flip a coin and then roll a fair six sided die. What is the probability the coin lands on heads up and the die shows an even number?
Answers
1. A spinner has an equal chance of landing on each of its eight numbered regions. After spinning, what is the probability you land on region three and region six?
In this case, the spinner's outcome of landing on region three is independent of landing on region six. Each spin is unrelated to the previous spin, and the outcome of one region does not affect the outcome of the other region. Therefore, the events are independent. The probability of landing on both region three and region six is the product of their individual probabilities: 1/8 * 1/8 = 1/64.
2. A bag contains six yellow jerseys numbered 1-6. The bag also contains four purple jerseys numbered 1-4. You randomly pick a jersey. What is the probability it is purple or has a number greater than 5?
In this scenario, the events are overlapping. A jersey can be both purple and have a number greater than 5 at the same time. Therefore, the probability of it being purple or having a number greater than 5 is the sum of their individual probabilities, minus the probability of the overlapping event (purple jerseys with a number greater than 5). There are 4 purple jerseys out of 10 total jerseys, and there is 1 jersey with a number greater than 5 out of 10. However, there is one jersey that satisfies both conditions (purple and number greater than 5), so we need to subtract it from the sum. So the probability is (4/10 + 1/10) - (1/10) = 4/10 = 2/5.
3. A box of chocolates contains six milk chocolates and four dark chocolates. Two of the milk chocolates and three of the dark chocolates have peanuts inside. You randomly select and eat a chocolate. What is the probability that it is a milk chocolate or has no peanuts inside?
In this scenario, the events are mutually exclusive. A chocolate cannot be both a milk chocolate and have no peanuts inside at the same time. Therefore, the probability of it being a milk chocolate or having no peanuts inside is the sum of their individual probabilities. There are 6 milk chocolates out of 10 total chocolates, and there are 7 chocolates without peanuts out of 10. So the probability is 6/10 + 7/10 = 13/10, which is greater than 1. However, probabilities cannot exceed 1, so we need to take the maximum value of 1. Therefore, the probability is 1.
4. You flip a coin and then roll a fair six-sided die. What is the probability the coin lands heads up and the die shows an even number?
In this case, the events are independent. The outcome of the coin flip does not affect the outcome of the die roll. The probability of the coin landing heads up is 1/2, and the probability of the die showing an even number is 1/2. To find the probability of both events occurring, we multiply their individual probabilities: 1/2 * 1/2 = 1/4.
I hope this clarifies the nature of each event. Let me know if you have any further questions!
The first question:
"A spinner has an equal chance of landing on each of its eight numbered regions. After spinning, what is the probability you land on region three and region six?"
Since the spinner has an equal chance of landing on each of its eight regions, the probability of landing on region three is 1/8, and the probability of landing on region six is also 1/8.
To find the probability of both events occurring (landing on region three and region six), you multiply the probabilities together:
P(landing on region three and region six) = P(landing on region three) * P(landing on region six) = (1/8) * (1/8) = 1/64.
Therefore, the probability of landing on both region three and region six is 1/64.
The events are mutually exclusive because it is not possible for the spinner to land on both region three and region six simultaneously.
--------------------------------------------------------------------------------------------------------------------------
The second question:
"A bag contains six yellow jerseys numbered 1-6. The bag also contains four purple jerseys numbered 1-4. You randomly pick a jersey. What is the probability it is purple or has a number greater than 5?"
To find the probability of either event occurring (purple or number greater than 5), we need to calculate the probabilities separately and then add them.
The probability of picking a purple jersey is 4/10 since there are four purple jerseys out of a total of ten jerseys.
The probability of picking a jersey with a number greater than 5 is 2/10 since there are two jerseys numbered 6 and above out of a total of ten jerseys.
To find the probability of either event occurring, we add the probabilities together:
P(purple or number greater than 5) = P(purple) + P(number greater than 5) = (4/10) + (2/10) = 6/10 = 3/5.
Therefore, the probability of picking a purple jersey or a jersey with a number greater than 5 is 3/5.
The events are overlapping since it is possible for the jersey to be both purple and have a number greater than 5.
--------------------------------------------------------------------------------------------------------------------------
The third question:
"A box of chocolates contains six milk chocolates and four dark chocolates. Two of the milk chocolates and three of the dark chocolates have peanuts inside. You randomly select and eat a chocolate. What is the probability that it is a milk chocolate or has no peanuts inside?"
To find the probability of either event occurring (milk chocolate or no peanuts inside), we need to calculate the probabilities separately and then add them.
The probability of selecting a milk chocolate is 6/10 since there are six milk chocolates out of a total of ten chocolates.
The probability of selecting a chocolate with no peanuts inside is 7/10 since there are seven chocolates without peanuts out of a total of ten chocolates.
To find the probability of either event occurring, we add the probabilities together:
P(milk chocolate or no peanuts inside) = P(milk chocolate) + P(no peanuts inside) = (6/10) + (7/10) = 13/10.
Therefore, the probability of selecting a milk chocolate or a chocolate with no peanuts inside is 13/10.
The events are mutually exclusive since a chocolate cannot be both a milk chocolate and have no peanuts inside simultaneously.
--------------------------------------------------------------------------------------------------------------------------
The fourth question:
"You flip a coin and then roll a fair six-sided die. What is the probability the coin lands heads up and the die shows an even number?"
The probability of the coin landing heads up is 1/2 since there are two possible outcomes (heads or tails) and they are equally likely.
The probability of rolling an even number on the die is 3
/6 or 1/2 since there are three even numbers (2, 4, and 6) out of a total of six possible outcomes.
To find the probability of both events occurring (coin lands heads up and die shows an even number), we multiply the probabilities together:
P(coin lands heads up and die shows an even number) = P(coin lands heads up) * P(die shows an even number) = (1/2) * (1/2) = 1/4.
Therefore, the probability of the coin landing heads up and the die showing an even number is 1/4.
The events are independent since the outcome of flipping the coin does not affect the outcome of rolling the die.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
How many website graphics can be created?

Answers
I do not understand what do you mean
A large bottle of juice contains 500 ml of juice, A medium bottle contains 70% as much juice as the large bottle. How many ml of juice is in the medium bottle. And why?
Answers
Answer:
10% = 500/10 = 50
So 10% is 50ml
10% x 7 = 70%
50 x 7 = 350ml
70% is 350ml
List all of the subgroups of S4. Find each of the following sets. Are any of these sets subgroups of S4?(a) {σ ∈ S4 : σ(1) = 3}(b) {σ ∈ S4 : σ(2) = 2}
Answers
This set {σ ∈ S4 : σ(1) = 3} contains the following elements of S4: (13), (23), (34), (24), (14), (12)(34), (13)(24), (14)(23) and {σ ∈ S4 : σ(2) = 2} this set contains the following elements of S4: (12), (21), (13)(24), (24)(13).
What are the subgroups of S4The group S4 is the symmetric group on 4 elements and has 24 elements. We can list all of its subgroups as follows:
The trivial subgroup {e}.Three subgroups isomorphic to the cyclic group of order 2: {e, (12)}, {e, (13)}, {e, (14)}.Four subgroups isomorphic to the cyclic group of order 3: {e, (123), (132)}, {e, (124), (142)}, {e, (134), (143)}, {e, (234), (243)}.Two subgroups isomorphic to the dihedral group of order 4: {e, (1234), (13)(24), (1432)}, {e, (1234), (14)(23), (1324)}.The alternating group A4 of even permutations: {e, (123), (132), (124), (142), (134), (143), (234), (243), (12)(34), (13)(24), (14)(23), (12)(34), (13)(24), (14)(23)}.Now, let's consider the sets (a) and (b) and see if they are subgroups of S4:
(a) {σ ∈ S4 : σ(1) = 3}
This set contains the following elements of S4: (13), (23), (34), (24), (14), (12)(34), (13)(24), (14)(23). We can check that this set is not a subgroup of S4 because it is not closed under composition. For example, (13)(14) = (134) is not in the set.
(b) {σ ∈ S4 : σ(2) = 2}
This set contains the following elements of S4: (12), (21), (13)(24), (24)(13). We can check that this set is a subgroup of S4. It is closed under composition, inverses, and contains the identity element e. Therefore, it is a subgroup of S4 and is isomorphic to the cyclic group of order 2.
Learn more on sets here;
https://brainly.com/question/13458417
#SPJ1
The area of the base of a portable speaker, shaped like a hexagonal prism, is 36 square inches. The height of the speaker is 8 inches. (The long side which it sits on in the image below is the height.) Find the volume of the speaker.
Answers
Answer:
92 dB
Step-by-step explanation:
Fsf
Answer:
\(volume = base \: area \times height \\ = 36 \times 8 \\ = 288 \: cubic \: inches\)
When ordering the Kids' Lunch at Burger Universe, the customer must choose a size, a type of bun, a side order, and a type of fruit drink. Here are the possibilities for each choice. Choice Possibilities Size: junior, Small, Medium, Large Type of bun Plain bun, Sesame seed bun Side order Fries, Onion rings Fruit drink Orange, Grape, Cherry, Lemonade How many Kids' Lunches are possible?
Answers
The number of Kid's Launches that are possible is 128. This is solved using Combination Principle.
What is combination in Math?A combination in mathematics is a selection of elements from a set with distinct members, where the order of selection is irrelevant.
Hence,
The number of possible "Sizes" from the specified 4 sizes are ⁴C₁
The number of sorts of bun that is possible from the specified two bun types is: ²C₁
From the four sides, the number of possible side purchases is: ⁴C₁
Of the available four drinks, the number of the possible drinks is: ⁴C₁
Now the possible number of all lunches are:
⁴C₁ x ²C₁ x ⁴C₁ x ⁴C₁
= 4 x 2 x 4 x 4
= 128
Hence the number of Kid's Lunches that are possible are 128.
Learn more about combination:
https://brainly.com/question/20211959
#SPJ1
I do not understand why the answer is a) for this equation: y'=2y+x. I assumed that the answer is c) or a), because numbers in the equation are positive, but I'm not sure this is the correct method here

Answers
The slope field for the differential equation would be D . Graph D .
What are slope fields ?A slope field provides a pictorial representation of differential equations that displays the magnitude and direction of the derivative or slope for solution curves at various points in the plane .
The length of line segments represents the magnitude, while the direction indicates the sign of the slope.
The equation given is y = 2 y + x which means that the slope is positive. This is why we can tell that Graph D has the correct slope field as it goes up for positive.
Find out more on slope fields at https://brainly.com/question/30194885
#SPJ1
Find Term 20 for the sequence a= 4 6 8 10......
Answers
4,6,8,10 are in A.P
a=4d=2\(\\ \rm\Rrightarrow a_n=a+(n-1)d\)
\(\\ \rm\Rrightarrow a_20=4+(20-1)2\)
\(\\ \rm\Rrightarrow a_20=4+19(2)\)
\(\\ \rm\Rrightarrow a_20=4+38\)
\(\\ \rm\Rrightarrow a_20=42\)
In the 2012 Olympics a U.S. athlete Nathan Adrian finished the 100-meter freestyle swim in 47.52 seconds. If nathan swam the same pace in a regular 25-meter pool what would his time have been per lap?
Answers
At the same rate as his 100-meter freestyle swim in the 2012 Olympics, Nathan Adrian could have completed one loop of a 25-meter pool in 11.88 seconds.
To solve this problem
The idea of proportionality can be applied. The time it would take Nathan Adrian to complete one lap in a 25-meter pool is known to be 47.52 seconds for the 100-meter freestyle. Since the tempo is constant while the distance varies, we can establish a ratio:
100 meters / 47.52 seconds = 25 meters / x seconds
where x is the unknown time for one lap in the 25-meter pool.
To solve for x, we can cross-multiply:
100 meters * x seconds = 47.52 seconds * 25 meters
100x = 1188
Dividing both sides by 100, we get:
x = 11.88 seconds
Therefore, at the same rate as his 100-meter freestyle swim in the 2012 Olympics, Nathan Adrian could have completed one loop of a 25-meter pool in 11.88 seconds.
Learn more about idea of proportionality here : brainly.com/question/870035
#SPJ1
Adrian wants to purchase an electric keyboard. The price of the keyboard at Macelli’s, with tax, is $2,400. He can save $150 per month. How long will it take him to save for the keyboard? (round to a full month).
Answers
It will take Adrian 16 full months to save enough money for the electric keyboard.
- Price of the keyboard (with tax) at Macelli's: $2,400
- Adrian's monthly savings: $150
We need to find how long it will take Adrian to save for the keyboard. To do this, we'll divide the total cost of the keyboard by his monthly savings and round up to the nearest full month.
Step 1: Divide the total cost by monthly savings.
Time (in months) = (Total Cost) / (Monthly Savings) = ($2,400) / ($150)
Step 2: Calculate the result.
Time (in months) = 16
So, it will take Adrian 16 full months to save enough money for the electric keyboard.
For more such questions on save , Visit:
https://brainly.com/question/18917547
#SPJ11
The sector of a circle has an area of 104pi/9
square inches and a central angle with measure 65 degree
. What is the radius of the circle, in inches?
Answers
Answer:
Given:
Area of the sector (A) = 104π/9 square inches
Central angle (θ) = 65 degrees
The formula for the area of a sector of a circle is:
A = (θ/360) * π * r^2
We can rearrange this formula to solve for the radius (r):
r^2 = (A * 360) / (θ * π)
Plugging in the given values:
r^2 = (104π/9 * 360) / (65 * π)
r^2 = (104 * 40) / 9
r^2 = 4160 / 9
r^2 ≈ 462.22
Taking the square root of both sides:
r ≈ √462.22
r ≈ 21.49
Therefore, the radius of the circle is approximately 21.49 inches.
Answer: 8 inches
Step-by-step explanation:
How much do you have to deposit today in order to have $5000 in two years?Assume the APR is 3% compounding quarterly.A. $625.00B. $4709.88C. $5307.99D. $4375.00
Answers
We are asked to find the principal for an amount compounded quarterly. Let's remember the formula for a future compounded quarterly:
\(A=P(1+\frac{r}{4})^{4t}\)We solve for P:
\(\frac{A}{(1+\frac{r}{4})^{4t}}=P\)We are given the following values:
\(\begin{gathered} A=5000 \\ r=0.03 \\ t=2 \end{gathered}\)Replacing we get:
\(\frac{5000}{(1+\frac{0.03}{4})^{(4)(2)}}=P\)Solving the operations:
\(4709.88=P\)Therefore, the initial value must be $4709.88
i promise this is my last one! BAHAHHAHA

Answers
Answer:
c 12 red marbles and 9(origninally i had 12 rad marbles and 8 blue i ment 9) blue marbles XD
Step-by-step explanation:can i get brainliest
Find the average rate of change of Find the average rate of change of
g
(
x
)
=
5
x
3
+
2
from
x
=
−
1
to
x
=
3
Answers
Answer:
eldinosauriocomera3.5kilos de carne :)
Step-by-step explanation:
What is your yearly median income if you are a male with an associate’s degree?
(Other question has been asked.)
Answers
The male with an associate degree has a yearly median income of $36,432.
What is median income?The median income means an income amount that divides a population into two equal groups, half having an income above that amount, and half having an income below that amount
The weekly income of a male with an associate degree is $759. We have 4 weeks in a month, and 12 months in a year. So, the yearly median income is:
= 4 *12 * $759
= $36,432
Therefore, the male with an associate degree has a yearly median income of $36,432.
Read more about median income
brainly.com/question/16488054
#SPJ1
Solve the following system of equations
y = -x^2+3x+18
y = -2x+4
A.) (-7.8) and (2,10)
B.) (2,20) and (11,-18)
C.) (-2,8) and (7,-10)
D.) (-2,-20) and (-11,18)
Answers
Answer:
\(\boxed{Option \ C}\)
Step-by-step explanation:
\(y = -x^2+3x+18\\y = -2x+4\)
Equating both equations
=> \(-x^2+3x+18 = -2x+4\\x^2-2x-3x+4-18 = 0\\x^2-5x-14=0\)
Using mid term break formula
=> \(x^2-7x+2x-14=0\\x(x-7)+2(x-7)=0\\Taking \ (x-7) \ common\\(x+2)(x-7) = 0\)
Either,
x + 2 = 0 OR x - 7 = 0
x = -2 OR x = 7
For, x = -2 , y is
=> y = -2x+4
=> y = -2(-2)+4
=> y = 4+4
=> y = 8
So, the ordered pair is (-2,8)
For x = 7 , y is
=> y = -2(7)+4
=> y = -14+4
=> y = -10
So, the ordered pair for this is (7, -10)
Solution Set = {(-2,8),(7,-10)}
Answer:
The answer is option C
Step-by-step explanation:
y = - x² + 3x + 18
y = - 2x + 4
Since they are both equal to y we equate them
That's,
- x² + 3x + 18 = - 2x + 4
x² - 5x - 14 = 0
Solve the quadratic equation
x² - 5x - 14 = 0
x² + 2x - 7x - 14 = 0
x(x + 2) - 7( x + 2) = 0
( x - 7)(x + 2) = 0
x - 7 = 0 x + 2 = 0
x = 7 x = - 2
Substitute the values of x into y = - 2x + 4
That's
when x = 7 when x = - 2
y = - 2(7) + 4 y = - 2(-2) + 4
y = - 14 + 4 y = 4 + 4
y = - 10 y = 8
So the solutions are
(7 , - 10) and ( - 2 , 8)Hope this helps you
Ronaldo specializes in creating sewing patterns for dresses, and wants to set up his own website to sell electronic copies. He pays $120 for a domain name and web hosting services for the first year. Ronaldo makes $14.25 for each electronic pattern that he sells. How many patterns must he sell to cover the cost of the website for the first year? Round your answer to a whole number.
Answers
Answer:
8
Step-by-step explanation:
120/14.25=8.4 rounded off to a whole number is 8
brainliest to best and correct answer please help

Answers
i need help pls
\( log10 \binom{30}{10} - 2 log10 \binom{5}{9} + log10 ( \frac{400}{343?})\)
Answers
Answer:
\(= log_{10} 11.33\\\)
Step-by-step explanation:
Given the expression;
\(log_{10}(\frac{30}{10} ) - 2log_{10} \frac{5}{9} + log_{10}(\frac{400}{343} )\)
Using the law of logarithm;
loga + logb = log(ab) and;
log a - log b = log(a/b)
The expression becomes;
\(= log_{10}(\frac{30}{10} ) + log_{10}(\frac{400}{343} )- 2log_{10} \frac{5}{9}\\= log_{10}(\frac{30}{10} ) + log_{10}(\frac{400}{343} )- log_{10} (\frac{5}{9})^2\\= log_{10}(\frac{30}{10} ) + log_{10}(\frac{400}{343} )- log_{10} \frac{25}{81}\\= log_{10}(\frac{30}{10} \times \frac{400}{343} \div \frac{25}{81})\\= log_{10}(\frac{30}{10} \times \frac{400}{343} \times \frac{81}{25})\\= log_{10}(\frac{3 \times 16 \times 81}{343} )\\= log_{10} \frac{3,888}{343} \\= log_{10} 11.33\\\)
9514 1404 393
Answer:
= log(3888/343)
= log(3888) -log(343)
= 4·log(2) +5·log(3) -3·log(7)
≈ 1.054432
Step-by-step explanation:
Perhaps you want to simplify and evaluate the logarithm.
The applicable rules are ...
log(a/b) = log(a) -log(b)
n·log(a) = log(a^n)
__
We will use "log" for "log10". So, your logarithm can be written as ...
log(30/10) -2·log(5/9) +log(400/343)
= log(3) +log(81/25) +log(400/343)
= log(3·81·400/(25·343)) = log(3888/343)
= log(3888) -log(343)
= log(2^4·3^5) -log(7^3) = 4·log(2) +5·log(3) -3·log(7) ≈ 1.054432
_____
Additional comment
My personal favorite form is the log of a fraction, as it requires the fewest calculator keystrokes. Perhaps the "simplest" is the weighted sum of the logs of primes.