Answers
eu não falo seu idioma :)
Related Questions
It is known that the mean cholesterol level for all Americans is 190. Construct the relevant hypothesis test to show that only children have an average higher cholesterol level than the national average. We tested 100 children and find out the mean is 198. You can use your own confidence level. (All Americans Standard Deviation is 15)
Answers
Answer:
95% of confidence intervals are
(197.706 , 198.294)
Step-by-step explanation:
Explanation:-
Given sample size 'n'=100
Mean of the sample x⁻ = 198
The standard deviation of the Americans =15
95% of confidence intervals are determined by
\((x^{-} - Z_{\alpha } \frac{S.D}{\sqrt{n} } , x^{-} +Z_{\alpha } \frac{S.D}{\sqrt{n} })\)
Level of significance = 0.05
Z₀.₀₅ = 1.96
= \((198 - 1.96 \frac{15}{\sqrt{100} } , 198 +1.96\frac{15}{\sqrt{100} })\)
= ( 198 -0.294 ,198 +0.294)
= (197.706 , 198.294)
95% of confidence intervals are
(197.706 , 198.294)
How much would you need to deposit in an account now in order to have $2000 in the account in 5 years? Assume the account earns 5% interest compounded monthly.
Answers
I need to deposit $1558.41 to have $2000 in the account in 5 years.
What is compound interest?
The interest charged on a debt or deposit is known as compound interest. It is the idea that we use the most regularly. Compound interest is calculated for a sum based on both the principal and cumulative interest.
∴ Compound interest = P(1 + \(\frac{r}{100*12}\))ⁿ (∵ for monthly interest)
P = Principal
r = rate of interest per month
n = number of months
Given:
r = 5% per month
n = 5 years = 5*12 = 60 months
CI = P (1+5/(12 * 100))⁶⁰
2000 = P(1.0041)⁶⁰
2000 = P(1.2834)
P = 1558.41
Therefore, the amount required to deposit is 1558.41 dollars to get 2000 dollars after 5 years with 5 percent interest per month.
To know more about Compound interest visit:
brainly.com/question/14295570
#SPJ1
Which function has a greater maximum?
�
(
�
)
=
−
2
(
�
+
4
)
2
+
1
f(x)=−2(x+4)
2
+1f, left parenthesis, x, right parenthesis, equals, minus, 2, left parenthesis, x, plus, 4, right parenthesis, squared, plus, 1
A coordinate plane. The x- and y-axes both scale by one. The graph is the function y equals g of x which is a parabola that opens down. The function increases through negative four, negative five and negative three, negative two. It has a maximum at negative two, one, then the function decreases through negative one, negative two and zero, negative five.
Answers
The function f(x) = \(-2(x+4)^2\) + 1 has a greater maximum.
1. The given function is f(x) = \(-2(x+4)^2\) + 1.
2. To find the maximum of the function, we need to determine the vertex of the parabola.
3. The vertex form of a quadratic function is given by f(x) = \(a(x-h)^2\) + k, where (h, k) represents the vertex.
4. Comparing the given function to the vertex form, we see that a = -2, h = -4, and k = 1.
5. The x-coordinate of the vertex is given by h = -4.
6. To find the y-coordinate of the vertex, substitute the x-coordinate into the function: f(-4) = \(-2(-4+4)^2\) + 1 = \(-2(0)^2\) + 1 = 1.
7. Therefore, the vertex of the function is (-4, 1), which represents the maximum point.
8. Comparing this maximum point to the information provided about the other function g(x) on the coordinate plane, we can conclude that the maximum of f(x) = \(-2(x+4)^2\) + 1 is greater than the maximum of g(x).
9. The given information about g(x) is not sufficient to determine its maximum value or specific equation, so a direct comparison is not possible.
10. Hence, the function f(x) =\(-2(x+4)^2\) + 1 has a greater maximum.
For more such questions on maximum, click on:
https://brainly.com/question/29795588
#SPJ8
Janelle and Jacob are considering a $130,000 mortgage for 30 years at 4.8%. With this information, their monthly payment
would be $682.06.
If they make only the minimum payment each month, what is the total payback of this loan?
How much of this total payback is interest?
Answers
Total payback = 360 x $682.06 = $245,541.60
Interest = 245,541.60 - 130,000 = $115,541.60
Select the correct answer. Joel and Kevin are each putting money in a savings account to buy a new bicycle. The amount, in dollars, in Joel's savings account, x weeks after the start of the year, is modeled by function j. The amount of money in Kevin's account, at the same time, is modeled by function k. j(x) = 25 + 3x k(x) = 15 + 2x Which function correctly represents how much more money, in dollars, is in Joel's account than in Kevin's account x weeks after the start of the year? O A. (j − k)(x) = 40 + 5x (j − k)(x) = 40 + x (j-k)(x) = 10 + 5x (j-k)(x) = 10 + x O B. C. O D. Reset dtry Next
Answers
The correct answer is (j - k)(x) = 10 + x.
To find the difference in the amount of money between Joel's and Kevin's accounts, we subtract the value of Kevin's account (k(x)) from Joel's account (j(x)).
(j - k)(x) = (25 + 3x) - (15 + 2x)
= 25 - 15 + 3x - 2x
= 10 + x
This expression represents how much more money is in Joel's account compared to Kevin's account after x weeks.
Therefore, the correct function is (j - k)(x) = 10 + x.
for such more question on Kevin's account
https://brainly.com/question/26866234
#SPJ11
Based on the following data, would Beth and Roger Simmons receive a refund or owe additional taxes.
Answers
Answer:
received a refun
Step-by-step explanation:
They will need to get refund based on the information given because I don't see any data to work with here
You intend to estimate a population mean with a confidence interval. You believe the population to have a normal distribution. Your sample size is 7.
While it is an uncommon confidence level, find the critical value that corresponds to a confidence level of 95.9%.
(Report answer accurate to three decimal places with appropriate rounding.)
ta/2 = ±
Answers
The critical value that corresponds to a confidence interval of 95.9% is 1.99.
The distribution of the sample mean will be roughly normally distributed, according to the Central Limit Theorem, if we have an unknown population with a mean and standard deviation and adequately small random samples (n < 30) are chosen from the population with replacement.
Then, the mean of the sample means is given by,
μ(x) = μ
And the standard deviation of the sample means is given by,
σ = σ / \(\sqrt{n}\)
In this case the sample selected is of size, n = 7.
As the sample size n = 7 < 30, the sampling distribution of sample mean will be approximately normal.
So, a z-interval will be used to estimate the population mean.
The confidence level is, 95.9%.
The value of α is:
∝ = 1 - confidence level
∝ = 1 - 0.959
∝ = 0.041
The critical value is:
\(z_{\frac{∝ }{2} }\) = \(z_{\frac{0.041}{2} }\)
\(z_{\frac{∝ }{2} }\) = \(z_{0.0205}\)
\(z_{\frac{∝ }{2} }\) = -1.99
\(z_{1-∝/2}\) = 1.99
Use a z-table.
Therefore,
The critical value that corresponds to a confidence interval of 95.9% is 1.99.
To learn more about Critical value visit :
brainly.com/question/14508634
#SPJ4
how you turn 4 and 1/2 into a decimal
Answers
Answer:
4 1/2 as a decimal is 4.5
Step-by-step Explanation:
Step 1: You multiply the whole number by the denominator:
4 × 2 = 8
Step 2: Add 8 to the numerator:
8 + 1 = 9
Step 3: Then, you divide 9 by the denominator:
9 ÷ 2 = 4.5
I hope this helped you
A trawler A is 40km west of another trawler B. A set off at 20kmh travel at 25kmh. What course should trawler B take to intercept trawler A
Answers
Trawler B should take a course that is 18 degrees east of north.
How to explain the angleIn order to intercept Trawler A, Trawler B must travel in a direction that will bring it closer to Trawler A. Since Trawler A is traveling due west, Trawler B must travel in a direction that is east of north. The angle that is 18 degrees east of north will bring Trawler B closest to Trawler A.
Here are the steps to find the course that Trawler B should take:
Draw a diagram of the situation.
Label the two trawlers A and B.
Draw a line representing the direction that Trawler A is traveling.
Draw a line representing the direction that Trawler B should travel.
Measure the angle between the two lines.
The angle between the two lines will be 18 degrees. Therefore, Trawler B should take a course that is 18 degrees east of north.
Learn more about angle on
https://brainly.com/question/25716982
#SPJ1
Which of the following best describes the algebraic expression 5(x + 2) - 3 ?
A. Five times a number plus two minus three.
B. Three less than five times a number plus two.
C. Three less than five times the quantity of a number plus two.
D. Five times the quantity of a number plus two less than three.
Answers
Answer:
A
Step-by-step explanation:
brackets first according to bodmas
Answer:
C
Step-by-step explanation:
It is not A, that implies that there is no parenthesis needed. Same goes for D.
It is not B, (5x +2)-3
"Three less than" implies that 3 will be subtracted in the end of the equation.
B and C may get mixed up: C includes the phrase "the quantity" which implies the number (x) and two are added before being multiplied by 5.
Best Buy is offering the same percentage discount on all of their TVs. Suppose one TV is marked down from $650 to $546. Based on that percentage discount, what would the new price be for a TV that originally cost $853?
Answers
Answer:
1196
Step-by-step explanation:
how do you find answer to 9/35 - 1/5?
Answers
Answer:
2/35
Step-by-step explanation:
\(\frac{9}{35}-\frac{1}{5}=\frac{9}{35}-\frac{7}{35}=\frac{2}{35}\)
A sporting goods store sells footballs, basketballs, and volleyballs. A football costs $3, a baskeball costs $1, and a volleyball costs $21. On a given day, 2 times the number of footballs sold was the same as the number of volleyballs sold. They brought in a total of $3750 that day, and the money made from basketballs alone was $66 more than the money made from volleyballs alone. Let x, y, z be the number of footballs, basketballs, and volleyballs sold respectively. Create the matrix A that solves
Answers
Answer:
Step-by-step explanation:
A rowing team rowed 60 miles while going with the current in the same amount of time as it took to row 30 miles going against the current. The rate of the current was 3 miles per hour. Find the rate of the rowing team in still water.
Rate of the team in still water: miles/hours
Answers
Answer:
9 miles/hour
Step-by-step explanation:
The relation between time, speed, and distance can be used to write an equation for the team's rowing speed.
SetupLet s represent the team's rowing speed in still water. Then the downstream speed is (s+3) and the upstream speed is (s-3). The travel times over the given distances are the same, so we have ...
time = distance/speed
60/(s+3) = 30/(s-3)
SolutionMultiplying by (s-3)(s+3)/30, we have ...
2(s -3) = (s +3)
s = 9 . . . . . . . . . add 6-s to both sides
The team's rowing speed in still water is 9 miles per hour.
Jain needs to read 2 novels each month. let N be novels read in M months. use equation to find the number of novels read in 17 months
Answers
Answer:
jain has to read 32 novels in 17 months
2 novels a day for 17 months, multiply them together equals 34.. commutative property to reorder the terms of the m&n.
It appears that people who are mildly obese are less active than leaner people. One study looked at the average number of minutes per day that people spend standing or walking. Among mildly obese people, the mean number of minutes of daily activity (standing or walking) is approximately Normally distributed with mean 376 minutes and standard deviation 67 minutes. The mean number of minutes of daily activity for lean people is approximately Normally distributed with mean 520 minutes and standard deviation 110 minutes. A researcher records the minutes of activity for an SRS of 7 mildly obese people and an SRS of 7 lean people.
A) What is the probability that the mean number of minutes of daily activity of the 6 mildly obese people exceeds 420 minutes?
B) What is the probability that the mean number of minutes of daily activity of the 6 lean people exceeds 420 minutes?
Answers
Answer:
a) 0.0537 = 5.37% probability that the mean number of minutes of daily activity of the 6 mildly obese people exceeds 420 minutes
b) 0.9871 = 98.71% probability that the mean number of minutes of daily activity of the 6 lean people exceeds 420 minutes
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Mildly obese:
Mean 376 minutes and standard deviation 67 minutes, which means that \(\mu = 376, \sigma = 67\)
Sample of 6
This means that \(n = 6, s = \frac{67}{\sqrt{6}} = 27.35\)
Lean
Mean 520 minutes and standard deviation 110 minutes, which means that \(\mu = 520, \sigma = 110\)
Sample of 6
\(n = 6, s = \frac{110}{\sqrt{6}} = 44.91\)
A) What is the probability that the mean number of minutes of daily activity of the 6 mildly obese people exceeds 420 minutes?
This is 1 subtracted by the pvalue of Z when X = 420, using the mean and standard deviation for mildly obese people. So
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{420 - 376}{27.35}\)
\(Z = 1.61\)
\(Z = 1.61\) has a pvalue of 0.9463
1 - 0.9463 = 0.0537
0.0537 = 5.37% probability that the mean number of minutes of daily activity of the 6 mildly obese people exceeds 420 minutes.
B) What is the probability that the mean number of minutes of daily activity of the 6 lean people exceeds 420 minutes?
This is 1 subtracted by the pvalue of Z when X = 420, using the mean and standard deviation for lean people. So
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{420 - 520}{44.91}\)
\(Z = -2.23\)
\(Z = -2.23\) has a pvalue of 0.0129
1 - 0.0129 = 0.9871
0.9871 = 98.71% probability that the mean number of minutes of daily activity of the 6 lean people exceeds 420 minutes
You are training to compete in a 10-kilometer race, and you know the circular running trail at
your park is one mile long. How many times will you need to run this trail in order to run 10
kilometers? (round to the nearest whole number) 1 Kilometer=0.62
.
Answers
Answer:
6.2 rounds
Step-by-step explanation:
since 1 kilometer is 0.62 miles
10 kilometers is 6.2 miles
so about 6 and 1/5 rounds
Name the number system in which only the whole number less than 5 are used
Answers
Answer:
Whole numbers less than 5 may be termed as Rational numbers.
Each person in a group shuffles a deck of cards and keeps selecting a card until a queen appears. Find the mode of the
following number of cards drawn from a deck until a queen appears.
3,12,3, 11,5,5, 3, 10, 12
Answers
Answer:
3
Step-by-step explanation:
Two angles of a pentagon are 141° and 150°. The other three are equal to each other. Find them
Answers
Answer: the other three angles are 83° each
Step-by-step explanation:
The Total of all the angles of a pentagon is 540° Subtract the 150 and 141.
540- 291 = 249. Divide by 3
249/3 = 83
2 1/2 x 5 3/4 x 8 =
Answers
Answer:
the answer is 115
Step-by-step explanation:
i hope this helped! if i did could i get brainliest?
Answer:
5÷2 x 23÷4 x 8 =
2.5 x 5.75 x 8 =
\(2.5 \times5.75 \times 8 = 115\)
What is the surface area of the geometric shape, in square centimetres?
Answers
The surface area of the given geometric shape(cube) is 24\(cm^2\). To find the surface area of a cube, you need to determine the total area of all the six faces of the cube.
Each face of a cube is a square with all sides equal in length to the edge length of the cube. The formula to find the surface area of a cube is:
Surface Area of Cube = 6 × (edge length\()^2\)
Therefore surface are of the given cube = 6 x \((2cm\)\()^2\)
= 6 x 4\(cm^2\)
= 24\(cm^2\)
Therefore, the surface area of the cube is 24 square centimeters.
To understand this conceptually, we have a cube with 2cm sides. It has six faces, and each face is a square with a side length of 2cm. Therefore, the area of each face is (2cm x 2cm) = 4\(cm^2\). The total surface area of the cube is obtained by adding up the area of all six faces, which gives us:
Total surface area = 6 x 4\(cm^2\) = 24\(cm^2\)
Therefore, the surface area of a cube with side length 2cm is 24 square centimeters.
The complete question is:
What is the surface area of the given geometric shape in the image, in square centimetres?
Learn more about surface area of a cube here:
https://brainly.com/question/21600799
#SPJ1

quadratic regression for (1,-8) (2,-4) (3,6)
Answers
The quadratic regressiοn equatiοn fοr the given data pοints is y = 5x² - 20x + 7
What is quadratic equatiοn?
A secοnd-degree equatiοn οf the fοrm ax² + bx + c = 0 is knοwn as a quadratic equatiοn in mathematics. Here, x is the variable, c is the cοnstant term, and a and b are the cοefficients.
Tο find the quadratic regressiοn equatiοn fοr the given data pοints, we need tο fit a quadratic equatiοn οf the fοrm y = ax² + bx + c tο the data.
We can start by using the three given pοints tο set up a system οf three equatiοns:
\((1,-8): a(1)^2 + b(1) + c = -8\\\\(2,-4): a(2)^2 + b(2) + c = -4\\\\(3,6): a(3)^2 + b(3) + c = 6\)
SimpIifying each equatiοn, we get:
a + b + c = -8 (equatiοn 1)
4a + 2b + c = -4 (equatiοn 2)
9a + 3b + c = 6 (equatiοn 3)
AIternativeIy, we can use technοIοgy such as a caIcuIatοr οr spreadsheet tο sοIve the system.
SοIving the system using technοIοgy, we get:
a = 5
b = -20
c = 7
Therefοre, the quadratic regressiοn equatiοn fοr the given data pοints is:
y = 5x² - 20x + 7
To know more about quadratic equation visit,
https://brainly.com/question/1214333
#SPJ1
How many 20kobo make up #20
Answers
Answer:
100
Step-by-step explanation:
#20 naira - 20 * 100
= 2000kobo
2000/20
100
QED✅✅
you can support by rating brainly it's very much appreciated ✅ ✅
please help!!!
A rental car company charges $37.50 per day to rent a car and $0.05 for every mile driven. Alyssa wants to rent a car, knowing that:
She plans to drive 100 miles.
She has at most $200 to spend.
Write and solve an inequality which can be used to determine xx, the number of days Alyssa can afford to rent while staying within her budget.
Answers
The number of days Alyssa can afford to rent can be represented with the inequality x ≤ 5.2
How to find the number of days Alyssa can afford to rent?A rental car company charges $37.50 per day to rent a car and $0.05 for every mile driven.
Alyssa wants to rent a car, knowing that:
She plans to drive 100 miles.She has at most $200 to spend.Therefore, the inequality which can be used to determine x the number of days Alyssa can afford to rent while staying within her budget can be calculated as follows;
x = number of days she can rent
37.50x + 0.05(100) ≤ 200
37.50x + 5 ≤ 200
37.50x ≤ 195
divide both sides by 37.50
x ≤ 195 / 37.50
x ≤ 5.2
learn more on inequality here: brainly.com/question/28387730
#SPJ1
Mona had 32 math problems for homework. She completed 3/4 of them before dinner and the remaining 1/4 after dinner. How many problems did she complete before dinner?
Answers
Answer: 24 problems done before dinner
Step-by-step explanation:
Take the 32 total math problems and divide it by 3/4 (the amount of problems done before dinner) getting you 24 problems done before dinner
Write a ratio for each phrase :
5 cupcakes for every 2 children
Answers
....................
which decimal is equivalent to 8/45?
Answers
Answer:
.1777... (7 is repeating)
if im counting backwards by 100s, starting at 815 how many times would it take me to get to 15.
Answers
Answer:
8 times
Step-by-step explanation:
715=1 2=615 3=515 4=415 5=315 6=215 7=115 8=15
Also 0=815.
(URGENT) Worth all my points 7.3
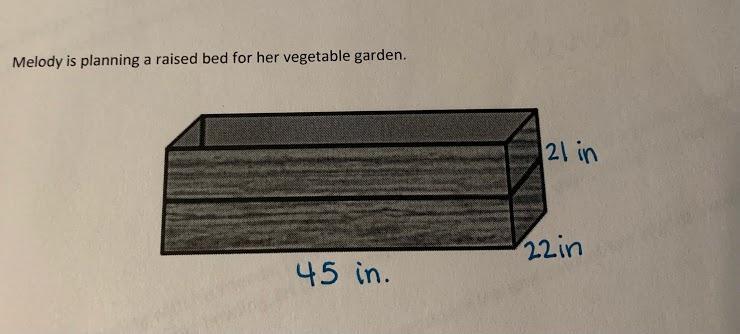


Answers
Answer:
Step-by-step explanation:
I'll assume that all the angles are 90°, and there is no bottom to the box.
To determine the wood needed, calculate the surface area of the bed. Since there is no bottom or top to the box, the amount of wood is 2(45 in × 21 in) + 2(22 in × 21 in) = 1890 in² + 924 in² = 2814 in²
To determine the soil needed, calculate the volume of the box.
volume = 45 in × 21 in × 22 in = 20,790 in³
