Answers
We have the folllowing:
\(\begin{gathered} m1=2x+40 \\ m2=2y+40 \\ m3=x+2y \\ m1=m3 \end{gathered}\)solving, m1 = m3
\(\begin{gathered} 2x+40=x+2y \\ 2x-x+40-2y=0 \\ x-2y+40=0 \end{gathered}\)Related Questions
Which of the following relations is a function?
a{(1, 3), (2, 3), (4,3), (9,3)}
b{(1, 2), (1, 3), (1, 4), (1,5)}
c{(5, 4), (-6, 5), (4, 5), (4, 0)}
d{(6,-1), (1,4), (2, 3), (6, 1)}
Answers
Answer:
a{(1, 3), (2, 3), (4,3), (9,3)}
Step-by-step explanation:
For the relation to be a function, each x can only go to 1 y
a{(1, 3), (2, 3), (4,3), (9,3)}
function
b{(1, 2), (1, 3), (1, 4), (1,5)}
x=1 goes to 4 different y's so not a function
c{(5, 4), (-6, 5), (4, 5), (4, 0)}
x=4 goes to 2 different y's so not a function
d{(6,-1), (1,4), (2, 3), (6, 1)}
x = 6 goes to 2 different y's so not a function
Option A is the answer since a function does NOT contain repeating x-values. In option A, it has the x-values of 1, 2, 4, 9 which do NOT repeat.
f(x) = cube root 2x
g(x) = 2x + 1
Find (f/g) (X) Include any restrictions on the domain

Answers
This might be help

After watching baking shows on T.V., Angie signs up for a cake-decorating class. To practice her new skills, she decorates a batch of cupcakes with sugar flowers. Angie puts 4 sugar flowers on each cupcake. In all, Angie puts 32 sugar flowers on the cupcakes.
Which equation can you use to find the number of cupcakes c Angie decorates?
Solve this equation for c to find the number of cupcakes Angie decorates.
Answers
Angie decorates 8 cupcakes after putting 4 sugar flowers on each cupcake.
To find the number of cupcakes c Angie decorates, we can use the equation:4c = 32where 'c' is the number of cupcakes Angie decorates.
4 represents the number of sugar flowers Angie puts on each cupcake, and 32 is the total number of sugar flowers Angie puts on the cupcakes.
To solve this equation for c, we need to isolate c on one side of the equation. We can do this by dividing both sides of the equation by 4. This gives us:c = 8
Therefore, Angie decorates 8 cupcakes.Here's how we get to this answer:4c = 32Divide both sides by 4 to isolate c:c/4 = 32/4c = 8
For more questions on isolate
https://brainly.com/question/11389214
#SPJ8
b. The sum of two consecutive integers is 109. Determine the integers in 4 steps.
Step 1:
Step 2:
Step 3:
Step 4:
Answers
The value of the first and second integers are 54 and 55 respectively.
What are the consecutive integers?Let
First integer = x
Second integer = x + 1
Sum of the integers = 109
So,
First integer + Second integer = Sum of the integers
x + (x + 1) = 109
x + x + 1 = 109
2x + 1 = 109
Subtract 1 from both sides
2x = 109 - 1
2x = 108
divide both sides by 2
x = 108/2
x = 54
Ultimately,
First integer = x
= 54
Second integer = x + 1
= 54 + 1
= 55
Therefore, the solution in 4 steps are;
Step 1: x + (x + 1) = 109
Step 2: 2x + 1 = 109
Step 3: 2x = 108
Step 4: x = 54
Read more on consecutive integers:
https://brainly.com/question/26352026
#SPJ1
The shorter leg of a right triangle is 14 feet less than the other leg. Find the length of the two legs if the hypotenuse is 34 feet.
Answers
Answer:
side a = 30 feet long.and side b = 30-14 = 16 feet long.
Step-by-step explanation:
Right triangle, with sides a, b=a-14 and h=34
By Pythagorean rule, h2 = 342 = a2 + b2 = a2 + (a-14)2 ==> a2 + a2 - 28a + 196
Simplify to get 1156 = 2a2 - 28a + 196
Subtract 1156 from both sides to get 2a2 - 28a - 960 = 0
Divide all terms by 2: a2 -14a - 480 = 0
Use quadratic equation to find that a = 30 or a = -16.
a = -16 will not work.
Therefore side a = 30 feet long.and side b = 30-14 = 16 feet long.
Check: 302 + 162 = 900+256=1156. SQRT(1156) = 34 feet, the given hypotenuse.Right triangle, with sides a, b=a-14 and h=34
By Pythagorean rule, h2 = 342 = a2 + b2 = a2 + (a-14)2 ==> a2 + a2 - 28a + 196
Simplify to get 1156 = 2a2 - 28a + 196
Subtract 1156 from both sides to get 2a2 - 28a - 960 = 0
Divide all terms by 2: a2 -14a - 480 = 0
Use quadratic equation to find that a = 30 or a = -16.
a = -16 will not work.
Therefore side a = 30 feet long.and side b = 30-14 = 16 feet long.
Check: 302 + 162 = 900+256=1156. SQRT(1156) = 34 feet, the given hypotenuse.
The side length of the other sides is 30 feet and 16 feet if the shorter leg of a right triangle is 14 feet less than the other leg.
What is a right-angle triangle?It is a triangle in which one of the angles is 90 degrees and the other two are sharp angles. The sides of a right-angled triangle are known as the hypotenuse, perpendicular, and base.
It is given that:
The shorter leg of a right triangle is 14 feet less than the other leg.
From the Pythagoras theorem:
hypotenuse² = perpendicula² + base²
perpendicular = base - 14
34² = (base - 14)² + base²
34² = base² - 28base + 196 + base²
2base² - 28base - 960 = 0
base = 30, -16
side length cannot be negative
base = 30 feet
The length of another leg:
perpendicular = 30 - 14 = 16 feet
Thus, the side length of the other sides is 30 feet and 16 feet if the shorter leg of a right triangle is 14 feet less than the other leg.
Learn more about the right-angle triangle here:
brainly.com/question/3770177
#SPJ2
Jean is planning to take a foreign language class. To research how satisfied other students are with their foreign language classes, she decides to take a sample of 50 such students. The university offers classes in five languages: Spanish, German, Russian, French, and Japanese. She will select a random sample of 10 students from each language class. Which term best describes the sampling technique Jean is using
Answers
Answer:
probability I think if I am ✅ can I get brainliyist
Aracely can spend up to a total of $20 on streamers
and balloons for a party. Streamers cost $1.49 per
pack, and balloons cost $4.39 per pack. Which of
the following inequalities represents this situation,
where is the number of packs of streamers Aracely
can buy, and b is the number of pack of balloons
Aracely can buy? (Assume there is no sales tax.)
Answers
Answer:
\(1.49S + 4.39B \leq 20\)
Step-by-step explanation:
The options are not given; However, the question can be solved without the list of options
Given
Let S represent packs of Streamers
Let B represent packs of Balloons
Required
Represent this with an inequality
From the question, we understand that;
\(1S\ =\ \$1.49\ and\ \ 1B\ = \ \$4.39\)
Also, it's stated that Aracely can't spend more than $20;
This mean that the maximum Aracely can spend is $20 and it can be represented with the inequality sign \(\leq 20\)
Bringing them together;
\(1.49S + 4.39B \leq 20\)
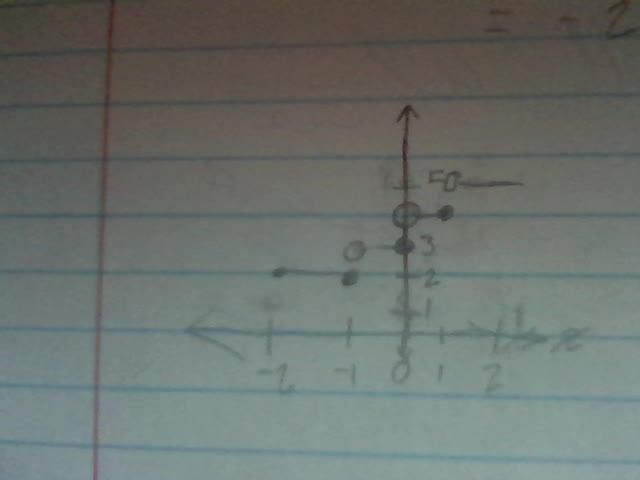
Need Help. ( Look at the picture). Will Mark Brainliest. Graph the step function over the interval. [ Please Show me on paper]. [ Only Answer if you truly know how to work this problem please and thank you]

Answers
I have an answer for you. This answer uses unclosed (white-center) holes to show "the value is not here" and closed (black-center) holes to show "the value is here." This step function is a "round up" of x+3, so it is exactly at y=3 at x=0.
Thank you for the Brainliest!
Find the equation of the line shown.

Answers
Answer:
y = -0.5x - 2
Step-by-step explanation:
y = mx + b
m is slope, change in y / change in x
slope = 1/2
b is y intercept
line intersects y axis at negative 2
therefore the equation is y = -0.5x - 2
Answer:
y = -0.5x - 2
Step-by-step explanation:
How many solutions does this system have? no solutions one unique solution O O two solutions O or an infinite number of solutions

Answers
Answer:
no solutions
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
equation of blue line is y = x + 2 , in slope- intercept form
with slope m = 1
equation of red line is y = x - 3 , in slope- intercept form
with slope m = 1
• Parallel lines have equal slopes
then the blue and red lines are parallel.
the solution to the system is at the point of intersection of the 2 lines
since the lines are parallel then they do not intersect each other.
thus the system shown has no solution.
PLEASE HELP ME ILL GIVE BRAINLIEST SELECT ALL THAT APLY!!!!!!!!!!!!!!!!!!!!!!!

Answers
\(y\cdot \:2\frac{1}{2} =\) \(2\frac{1}{2}=\frac{2\cdot 2+1}{2}=\frac{5}{2}\) \(=\frac{5y}{2}\)
a) \(2y+\frac{1}{2}=\frac{4y+1}{2}\)
b) \(2y+\frac{1}{2}y=\frac{5y}{2}\)
So b) is the expression that is equivallent.Hope I helped you!Success!what is the smallest possible average of five distinct positive even integers
Answers
Answer:
2+4+6+8+10/5
10 is average of this
The smallest possible average of five distinct positive even integers is 6.
To find the smallest possible average of five distinct positive even integers, to minimize the values of those integers.
The smallest distinct positive even integers start from 2, 4, 6, 8, 10, and so on.
To minimize the average, to choose the five smallest even integers. So, the five distinct positive even integers are:
2, 4, 6, 8, 10
To calculate the average, sum up these five integers and divide by 5:
Average = (2 + 4 + 6 + 8 + 10) / 5
Average = 30 / 5
Average = 6
So, the smallest possible average of five distinct positive even integers is 6.
Learn more about Integers here:
https://brainly.com/question/33503847
#SPJ3
calculate the Area of parallelogram GDEF if the base is 5m and the altitude is 3,2m
Answers
Step-by-step explanation:
the area of a parallelogram is
baseline × height = 5 × 3.2 = 16 m²
HELP ME. I HATE MATH DUDE.

Answers

Your bank offers a promotion where they'll give you $5 for every $100
you deposit into a savings account.
If you deposit $800, how much will the bank give you?
$45
$50
$60
$40
Answers
Answer: C. Forty dollars.
Step-by-step explanation: $5 times eight hundreds equals forty, therefore you will get $40 from the bank.
40 if u take 100 8 times then it will be 800 and You only times 8by 5 then or 5by 8
also if possible can i have brainliest
WILL GIVE 5 STARS
Angela plays soccer and golf for a total of 125 minutes every day. She plays soccer 45 minutes more than she plays golf.
Part A: Write a pair of linear equations to show the relationship between the number of minutes Angela plays soccer (x) and the number of minutes she plays golf (y) every day. (5 points)
Part B: How much time does Angela spend playing golf every day? (3 points)
Part C: Is it possible for Angela to have spent 80 minutes playing soccer every day? Explain your reasoning.
Answers
A: The linear equations are x + y = 125 and x = y + 45.
B: Everyday Angela spends 40 minutes in playing golf.
C: No, it is not possible for Angela to spend 80 minutes playing soccer every day.
What is a linear equation?
A linear equation is one that has a degree of 1 as its maximum value. No variable in a linear equation, thus, has an exponent greater than 1. A linear equation's graph will always be a straight line.
Part A:
Let x be the number of minutes Angela plays soccer every day
Let y be the number of minutes Angela plays golf every day
According to the problem statement the linear equations are -
x + y = 125 (total time playing both sports is 125 minutes)
x = y + 45 (Angela plays 45 more minutes of soccer than golf)
Part B:
Substitute x = y + 45 into the first equation -
(y + 45) + y = 125
Use the addition operation -
2y + 45 = 125
2y = 80
y = 40
Angela spends 40 minutes playing golf every day.
Part C:
If Angela spends 80 minutes playing soccer every day, then
x = 80
y + 45 = 80 (using the equation x = y + 45)
y = 35
But this would mean that she plays golf for 35 minutes and soccer for 80 minutes, which adds up to a total of 115 minutes.
This is not possible since the problem states that Angela plays both sports for a total of 125 minutes every day.
Therefore, it is not possible for Angela to have spent 80 minutes playing soccer every day.
To learn more about linear equation from the given link
https://brainly.com/question/2226590
#SPJ1
50 points! Please help fast. I will mark brainliest. Random answers will be reported

Answers
Answer:
-2,-4
Step-by-step explanation:
RANDOM!
2+2+351+8 please answer
Answers
Answer:
363
Step-by-step explanation:
2+2+351+8 = 363
f(x) = -2x^2+3x-6
how does the function open
Answers
To increase an amount by 48% multiply by
Answers
0.48
Step-by-step explanation:
to increase an amount by 48%
you divide 48 with 100 to find the multiplier
which is 0.48
multiply 0.48 to an number to find 48%
Someone, please help me! If you give it right, ill give you Brainiest.
If you don't know the answer, please don't comment.
Can you explain every step you have to do to solve √(24^2 + 12^2?)
Answers
Answer:
\( \sqrt{576 + 144} \)
\( \sqrt{720} \)
\( \sqrt{12^{2} } \times \sqrt{5} \)
\({12 \times \sqrt{5} } \)
what is the solution to the equation:
5(n - 1/10) = 1/2
a. n= 13/5
b. n= 3/25
c. n= 0
d. n= 1/5
Answers
\( \sf \longrightarrow \: 5 \bigg( \: n - \frac{1}{10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: 5 \bigg( \: \frac{n}{1} - \frac{1}{10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: 5 \bigg( \: \frac{10 \times n - 1 \times 1}{1 \times 10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: 5 \bigg( \: \frac{10n - 1}{ 10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: \: \frac{50n - 5}{ 10} = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: \: 2(50n - 5) =1(10) \\ \)
\( \sf \longrightarrow \: \: 2(50n - 5) =10 \\ \)
\( \sf \longrightarrow \: \: 100n - 10=10 \\ \)
\( \sf \longrightarrow \: \: 100n =10 + 10\\ \)
\( \sf \longrightarrow \: \: 100n =20\\ \)
\( \sf \longrightarrow \: \:n = \frac{2 \cancel{0}}{10 \cancel{0}} \\ \)
\( \sf \longrightarrow \: \:n = \frac{1}{5} \\ \)
Answer:-
Answer:- D) n = ⅕ ✅To solve the equation \(\sf 5(n - \frac{1}{10}) = \frac{1}{2} \\\) for \(\sf n \\\), we can follow these steps:
Step 1: Distribute the 5 on the left side:
\(\sf 5n - \frac{1}{2} = \frac{1}{2} \\\)
Step 2: Add \(\sf \frac{1}{2} \\\) to both sides of the equation:
\(\sf 5n = \frac{1}{2} + \frac{1}{2} \\\)
\(\sf 5n = 1 \\\)
Step 3: Divide both sides of the equation by 5 to isolate \(\sf n \\\):
\(\sf \frac{5n}{5} = \frac{1}{5} \\\)
\(\sf n = \frac{1}{5} \\\)
Therefore, the solution to the equation \(\sf 5(n - \frac{1}{10})\ = \frac{1}{2} \\\) is \(\sf n = \frac{1}{5} \\\), which corresponds to option (d).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Use: 0, 4, 6, 11, 9, 8, 9, 1, 5, 9, 7 to construct a box-and-whisker plot. List the maximum, minimum, and quartiles below. has to be a sentence
Answers
A box-and-whisker plot which represent the given data set is shown in the image attached below.
The five-number summary for the given data set have been listed correctly below.
What is a box-and-whisker plot?In Mathematics, a box-and-whisker plot is sometimes referred to as a box plot and it can be defined as a type of chart that is used for the graphical or visual representation of the five-number summary of a data set with respect to locality, skewness, and spread.
By using an online box-and-whisker plot calculator, the five-number summary for the given data set include the following:
Minimum = 0.First quartile = 4.Median = 7.Third quartile = 9.Maximum = 11.By critically observing the box-and-whisker plots (see attachment), we can logically deduce that all of the five-number summary for the given data set are correctly listed.
Read more on box plot here: brainly.com/question/14277132
#SPJ1

PLEASE HELP WITH FACTORING PROBLEM/SHOW WORK!

Answers
Answer:
(3x+2)(x-5)
Step-by-step explanation:
Factor by grouping
\(3x^2-13x-10\\=3x^2-15x+2x-10\\=3x(x-5)+2(x-5)\\=(3x+2)(x-5)\)
Solve for angles x and y in the triangle below. Round your angle to the nearest whole degree.
Solve for both x and y

Answers
\(\tan(y )=\cfrac{\stackrel{opposite}{6}}{\underset{adjacent}{4}} \implies \tan( y )= \cfrac{3}{2} \implies \tan^{-1}(~~\tan( y )~~) =\tan^{-1}\left( \cfrac{3}{2} \right) \\\\\\ y =\tan^{-1}\left( \cfrac{3}{2} \right)\implies y \approx 56.31^o \\\\[-0.35em] ~\dotfill\\\\ \tan(x )=\cfrac{\stackrel{opposite}{4}}{\underset{adjacent}{6}} \implies \tan( x )= \cfrac{2}{3} \implies \tan^{-1}(~~\tan( x )~~) =\tan^{-1}\left( \cfrac{2}{3} \right) \\\\\\ x =\tan^{-1}\left( \cfrac{2}{3} \right)\implies x \approx 33.69^o\)
Make sure your calculator is in Degree mode.
Help me out here pleaseeeeee

Answers
Answer:
C
Step-by-step explanation:
secx - 2=0
(a) x= pi/3
Answers
Step-by-step explanation:
secx - 2=0
secx= 2
x= π/3
that's it
The x-values that satisfy the equation Sec(x) - 2 = 0 are x = π/3 and x = 5π/3.
To verify the given equation, we need to find the value(s) of x that satisfy the equation Sec(x) - 2 = 0.
Sec(x) represents the secant function, which is the reciprocal of the cosine function.
The equation can be rewritten as follows:
Sec(x) = 2
To find the solutions, we can take the reciprocal of both sides:
1 / Cos(x) = 2
Next, we can invert the equation to get the cosine function alone:
Cos(x) = 1/2
The cosine function has a value of 1/2 at two specific angles in the interval [0, 2π]: π/3 and 5π/3.
These angles correspond to the inverse cosine function (arccos), so we have:
x = arccos(1/2) = π/3 or x = arccos(1/2) + 2π = 5π/3
Therefore, the x-values that satisfy the equation Sec(x) - 2 = 0 are x = π/3 and x = 5π/3.
Learn more about secant function click;
https://brainly.com/question/1673663
#SPJ6
A rectangular paperboard measuring 20in long and 12in wide has a semicircle cut out of it, as shown below. What is the perimeter of the paperboard that remains after the semicircle is removed? (Use the value 3.14 for pi , and do not round your answer. Be sure to include the correct unit in your answer.)
Answers
A semicircle has been cut out of a rectangular paperboard that is 20 inches long and 12 inches broad, as seen below. After the semicircle is taken out, the paperboard's remaining perimeter is 34.58 inches.
The paperboard has a length of 20 inches and a width of 12 inches. A semicircle is cut out of it, which means we need to find the perimeter of the remaining part.
The diameter of the semicircle is equal to the width of the paperboard, which is 12 inches. So, the radius of the semicircle is half of the diameter, which is 6 inches.
The perimeter of the remaining part will be the sum of the length of the paperboard and the two straight sides of the semicircle.
The length of the paperboard is 20 inches, and the two straight sides of the semicircle are equal to the diameter of the semicircle, which is 12 inches. So, the perimeter of the remaining part is:
P = 20 + 12 + 12 = 44 inches
However, we also need to subtract the length of the curved part of the semicircle from the perimeter. The length of the semicircle can be found using the formula:
C = πr
where C is the circumference of the semicircle and r is the radius.
Since we have a semicircle, we need to divide the circumference by 2. So, the length of the curved part of the semicircle is:
C/2 = (π x 6) / 2 = 9.42 inches (rounded to two decimal places)
Therefore, the perimeter of the remaining part is:
P = 44 - 9.42 = 34.58 inches (rounded to two decimal places)
So, the perimeter of the remaining paperboard is 34.58 inches.
To learn more about perimeter, refer:-
https://brainly.com/question/6465134
#SPJ1
Evaluating Linear Piecewise Functions
Consider the function:
f(x) =
7/2+ 2x, x≤-1
-5+3x/2, -1
1/4x, x≥3
< -5_-4_-3_-2_-1_0_1_2_3_4_5 >
What are these values?
f(-3) =[-19/2]ᵒʳ[-5/2]ᵒʳ[-3/4]ᵒʳ[5/2]
f(-1) =[-13/2]ᵒʳ[-3/2]ᵒʳ[-1/4]ᵒʳ[-3/2]
f(3) =[-7/4]ᵒʳ[-1/2]ᵒʳ[3/4]ᵒʳ[19/2]
PLEASE HELP ME ON A SERIOUS TIME CRUNCH!!

Answers
-3≤-1, so we must use the 7/2+2x function.
Insert x into the function that has a true domain statement:
f(-3)=7/2+2(-3)
Evaluate:
f(-3)=7/2-6
Obtain a common denominator to subtract fractions:
f(-3)=7/2-(6•2/1•2)
Remember, -6 is equivalent to -6/1, so we multiply the numerator and denominator by 2 to get a common denominator.
Simplify:
f(-3)=7/2-12/2
Subtract the numerators only; denominators stay as 2:
f(-3)=(7-12)/2
Answer: f(-3)=-5/2
—————————————————————
f(-1)
-1≤-1, so we must use the 7/2+2x function again. We must always check x in all domain piecewise cases.
Let’s evaluate f(-1):
f(-1)=7/2+2(-1)
f(-1)=7/2-2
Obtain a common denominator; -2=-2/1:
f(-1)=7/2-(2•2/1•2)
f(-1)=7/2-4/2
f(-1)=(7-4)/2
Answer: f(-1)=3/2
—————————————————————
f(3)
Let’s check all domain cases. We see the only true statement is: 3≥3, so we must use the 1/4x function.
f(3)=1/4(3)
Answer: f(3)=3/4
Hope this helps! Please give Brainliest
What is the rule for the function that is graphed?

