Calcula el area y perímetro de un triángulo equilátero de 5.9 cm de lado
Answers
The area of an equilateral triangle is 15.073 square centimeter and the perimeter is 17.7 centimeter.
Given that, each side of an equilateral triangle is 5.9 cm.
Here, perimeter of an equilateral triangle is 3a, where a is edge of an equilateral triangle.
So, the perimeter of an equilateral triangle = 3×5.9
= 17.7 cm
We know that, area of an equilateral triangle = √3/4 ×a²
= √3/4 ×5.9²
= 15.073 square centimeter
Therefore, the area of an equilateral triangle is 15.073 square centimeter and the perimeter is 17.7 centimeter.
#SPJ1
Related Questions
4c-5=-6 what is rye value of c ????? and 5e+2=9 what is the value of e??
Answers
Answer:
c = -1/4
e = 1 2/5
Step-by-step explanation:
4c - 5 = -6
add 5 to both sides
4c = -1
divide each side by 4
c = -1/4
5e + 2 = 9
subtract 2 from both sides
5e = 7
divide both sides by 5
e = 1 2/5
-Chetan K
Answer:
c = -1/4
e = 7/5
Step-by-step explanation:
1. 4c - 5 = -6, 4c = -1, c = -1/4
2. 5e + 2 = 9, 5e = 7, e = 7/5
A simple pulley with the give radius 4 in used to lift heavy objects is positioned 10 feet above ground level. Given that the pully rotates 720 degrees determine the height yo which the object is lifted.
Answers
9514 1404 393
Answer:
50.3 inches
Step-by-step explanation:
720 degrees is 2 full turns, or twice the circumference of the pulley. The circumference is given by ...
C = 2πr
C = 2π(4 in) = 8π in
Then 2 times that is ...
height lifted = 2(8π in) = 16π in ≈ 50.3 in
The object was lifted about 50.3 inches.
Which equation describes the line graphed above?

Answers
You and a friend are playing a board game. your final score $x$ is $12$ points less than your friend's final score. write and solve an equation to find your final score. round 9 round 10 final score your friend 22 12 195 you 9 25 ? equation: $=195$ your final score is points.
Answers
The equation formed using the given data is 195 = x + 12 and your final score is 183 points.
How to form an equation?
Determine the known quantities and designate the unknown quantity as a variable while trying to set up or construct a linear equation to fit a real-world application.
In other words, an equation is a set of variables that are constrained through a situation or case.
Let's say your final score is x
Given that,
Your final score x is 12 points less than your friend's final score.
So,
x = friend final score - 12
Now,
Friend final score = 195
So,
x = 195 - 12
x + 12 = 195
195 = x + 12
Now,
x = 195 - 12 = 183
Hence "The equation formed using the given data is 195 = x + 12 and your final score is 183 points".
For more about the equation,
brainly.com/question/10413253
#SPJ4
sixteen is four less than half of x
16 = 4 - 2x
16 = x ^ 2 - 4
16 = 1/2 x - 4
16 = 4 - 1/2 x
Answers
Answer:
16+1/2x-4
Step-by-step explanation:
what is e * 6 - 4 * 1
Answers
Answer:
14 is the answer if you mean 3 by that e
Apply a 90 degree rotation to the point (1, 2)
Answers
Answer:
(-1,2)
Step-by-step explanation:
90 degree rotation from (a,b) is (-a,b)
two cyclists, 42 miles apart, start riding toward each other at the same time. one cycles 2 times as fast as the other. if they meet 2 hours later, what is the speed (in mi/h) of the faster cyclist?
Answers
The speed of the faster cyclist is 14\ miles/hr.
What is speed?
It is the average distance coverd in unit time. It is also defined as the rate of change of distance with respect to time.
Since the speed of the first cyclist is double than the second cyclist hence, the first cyclist will cover the double distance than the second cyclist. Consider the first cyclist covers 2s distance and first cyclist covers s distance. The sum of these two distances should be 42 miles. Hence,
\(2s+s=42\\3s=42\\s=14\)
Now, distance coverd by the first cyclist is \(2s=2\times 14\\=28 \ $miles\).
Now, both the cyclists meet after 2 hr hence, time taken by the first cyclist is 2 hr.
\(Speed=\frac{Total\ distance}{Total\ time}\\=28\ miles/2 \ hr\\=14\ miles/hr\)
Hence, the speed of the faster cyclist is 14\ miles/hr.
Learn more about speed from the following link:
https://brainly.com/question/13943409
#SPJ4
m∠2=(7x−11)∘ and m∠4=(4x+4)∘
What is m∠1 ?

Answers
Answer:
Step-by-step explanation:
7x-11=4x+4(being vertically opposite abgles)
7x-4x=4+11
3x=15
x=15/3
x=5
angle 2+angle1=180 degree(being straight line)
7x-11+angle 1=180
7*5-11+angle 1=180
35-11+angle1=180
24+angle 1=180
angle 1=180-24
angle 1=156 degree
30 In right triangle PRT, m/P = 90°, altitude PQ is drawn to hypotenuse RT. RT = 17, and
PR = 15.
Determine and state, to the nearest tenth, the length of RQ
Answers
Using the cosine ratio formula, the length of RQ to the nearest tenth is: 13.2.
What is the Cosine Ratio Formula?The cosine ratio formula is given as, cos ∅ = length of adjacent side / length of hypotenuse.
Find m∠PRT in ΔPRT using the cosine ratio formula:
cos(m∠PRT) = 15/17
m∠PRT = cos^(-1)(15/17)
m∠PRT ≈ 28.07°
Find RQ in ΔPRQ using the cosine ratio formula:
cos(28.07) = RQ/15
RQ = cos(28.07) × 15
RQ ≈ 13.2
Learn more about the cosine ratio formula on:
https://brainly.com/question/9027282
#SPJ1

Suppose a certain trial has a 60% passing rate. We randomly sample 200 people that took the trial. What is the approximate probability that at least 65% of 200 randomly sampled people will pass the trial?
Answers
The approximate probability that at least 65% of the 200 randomly sampled people will pass the trial is approximately 0.9251 or 92.51%
What is the approximate probability that at least 65% of 200 randomly sampled people will pass the trial?To calculate the approximate probability that at least 65% of the 200 randomly sampled people will pass the trial, we can use the binomial distribution and the cumulative distribution function (CDF).
In this case, the probability of success (passing the trial) is p = 0.6, and the sample size is n = 200.
We want to calculate P(X ≥ 0.65n), where X follows a binomial distribution with parameters n and p.
To approximate this probability, we can use a normal distribution approximation to the binomial distribution when both np and n(1-p) are greater than 5. In this case, np = 200 * 0.6 = 120 and n(1-p) = 200 * (1 - 0.6) = 80, so the conditions are satisfied.
We can use the z-score formula to standardize the value and then use the standard normal distribution table or a calculator to find the probability.
The z-score for 65% of 200 is:
z = (0.65n - np) / √np(1-p))
z = (0.65 * 200 - 120) /√(120 * 0.4)
z = 1.44
Looking up the probability corresponding to a z-score of 1.44in the standard normal distribution table, we find that the probability is approximately 0.0749.
However, we want the probability of at least 65% passing, so we need to subtract the probability of less than 65% passing from 1.
P(X ≥ 0.65n) = 1 - P(X < 0.65n)
P(X ≥ 0.65) =1 - 0.0749
P(X ≥ 0.65) = 0.9251
P = 0.9251 or 92.51%
Learn more on probability here;
https://brainly.com/question/23286309
#SPJ4
Is question 6 and question 7 is it correct

Answers
Answer:
6) a
7) c
Step-by-step explanation:
question 6 is incorrect because you have to find the distance between the two points. for question 6, you are finding the distance between -2 and 1. that is three!
Square ABCD has an area of 64 units^2
2
. It is rotated 270^{\circ}
∘
clockwise around vertex C resulting in square A'B'C'D'.
What is the side length of C'D'?
Answers
On solving the provided question, we got to know that side length of the square is 8 units.
What is a square?Four sides that are equally spaced apart make up a square. Around us, a lot of things are rectangular. Equal sides and a 90° interior angle serve as a visual cue to identify a square. A closed square has four sides and exists in two dimensions (2D). A square has an equal number and parallel alignment of its four sides.
What to identify a square?A four-sided shape known as a square has sides that are all the same length and angles that are all right angles with a 90 degree angle.
Here,
Area of square = \((side)^2\)
64 = \((side)^2\)
\(Side = \sqrt{64}\)
Side = 8 units
To know more about square visit:
https://brainly.com/question/28776767
#SPJ1
hat is the variance of the number of fixed elements, that is, elements left in the same position, of a randomly selected permutation of n elements? [hint: let x denote the number of fixed points of a random permutation. write x
Answers
Let X be the number of fixed points of a random permutation of n elements. A fixed point is an element that remains in the same position after the permutation. Thus, the probability that an element is fixed is 1/n, and the probability that it is not fixed is (n-1)/n.
Using the linearity of the expected value, we can calculate the expected value of X as:
E(X) = E(X1 + X2 + ... + Xn) = E(X1) + E(X2) + ... + E(Xn)
where Xi is the indicator random variable that is equal to 1 if the i-th element is fixed and 0 otherwise. Since the probability of an element being fixed is 1/n, we have E(Xi) = 1/n. Therefore,
E(X) = n * (1/n) = 1
To find the variance of X, we need to compute E(X^2) - E(X)^2. We can use the fact that X^2 = X1 + X2 + ... + Xn, where Xi is the indicator random variable that is equal to 1 if the i-th and j-th elements are both fixed and 0 otherwise. Then,
E(X^2) = E(X1 + X2 + ... + Xn)^2 = E(X1^2 + X2^2 + ... + Xn^2) + 2 E(X1X2 + X1X3 + ... + X(n-1)n)
Since there is only one way to fix two elements out of n, we have E(XiXj) = 1/(n(n-1)). Therefore,
E(X^2) = n * (1/n) + n(n-1) * (1/(n(n-1))) = 1 + 1/n
Finally, the variance of X is
Var(X) = E(X^2) - E(X)^2 = 1 + 1/n - 1^2 = 1/n
Therefore, the variance of the number of fixed elements of a randomly selected permutation of n elements is 1/n.
To learn more about permutation : brainly.com/question/1216161
#SPJ11
Which is a correct first step for solving this equation? 8−2(3−x)=4x+6 CLEAR CHECK Math item response image Math item response image Math item response image Math item response image
Answers
Answer:
The first thing that you would need to do is slove for your parentheses.
Step-by-step explanation:
PEMDAS
Answer:
Parentheses
Step-by-step explanation:
PEMDAS
For the curve r(t), find an equation for the indicated plane at the given value of t.
-r(t) = (t2 - 8)i + (2t - 5)j + 8k; osculating plane at t = 6.
A) x + y + (z + 8) = 0
B) z = -8
C) x + y + (z - 8) = 0
D) z = 8
Answers
To find the equation for the osculating plane of the curve at t = 6, we first need to calculate the position vector r(6) and the velocity vector v(6) at that specific value of t.
Given r(t) = (t^2 - 8)i + (2t - 5)j + 8k, we substitute t = 6 into the equation:
r(6) = (6^2 - 8)i + (2(6) - 5)j + 8k
= 28i + 7j + 8k
The position vector r(6) is equal to 28i + 7j + 8k.
Next, we calculate the velocity vector at t = 6:
v(6) = d(r(t))/dt = (2t)i + 2j
v(6) = (2(6))i + 2j
= 12i + 2j
Now, we can write the equation for the osculating plane using the position vector r(6) and the velocity vector v(6):
(x - 28)i + (y - 7)j + (z - 8)k • (12i + 2j) = 0
Simplifying this equation gives:
x - 28 + y - 7 + 12z - 96 + 2z - 16 = 0
x + y + 14z - 147 = 0
Therefore, the equation of the osculating plane at t = 6 is x + y + 14z - 147 = 0.
The correct answer is not listed among the options provided.
Learn more about velocity here: brainly.com/question/32263626
#SPJ11
an archaeologist uncovers 26 artifacts from a site. the types of artifacts are shown. an artifact is randomly selected for display. a bar-graph titled archeological artifacts. the horizontal axis represents tools, pottery, and coins. the vertical axis represents number of artifacts and ranges from 0 to 16, in increments of 2. number of artifacts of tools is 14. number of artifacts of pottery is 7. number of artifacts of coins is 5. what is the probability that a piece of pottery is selected? express your first answer as a fraction in simplest form, and round your percent answer to the nearest whole percent. or about %
Answers
The probability of selecting a piece of pottery is 7/26, and when converted to a percentage and rounded to the nearest whole percent, it is approximately 27%.
An archaeologist uncovers 26 artifacts from a site. The types of artifacts are shown below. The horizontal axis represents tools, pottery, and coins. The vertical axis represents the number of artifacts and ranges from 0 to 16, in increments of 2. The number of artifacts of tools is 14. The number of artifacts of pottery is 7. The number of artifacts of coins is 5.
What is the probability that a piece of pottery is selected?The total number of artifacts at the site = 26
Number of pottery artifacts = 7
Probability of selecting a piece of pottery = Number of pottery artifacts/Total number of artifacts
Probability of selecting a piece of pottery = 7/26
If we want to express this probability in a percentage, we can convert it by multiplying it by 100.
Thus,Probability of selecting a piece of pottery = 7/26 = 0.269 = 26.9% (rounded to the nearest whole percent)
for such more question on probability
https://brainly.com/question/24756209
#SPJ11
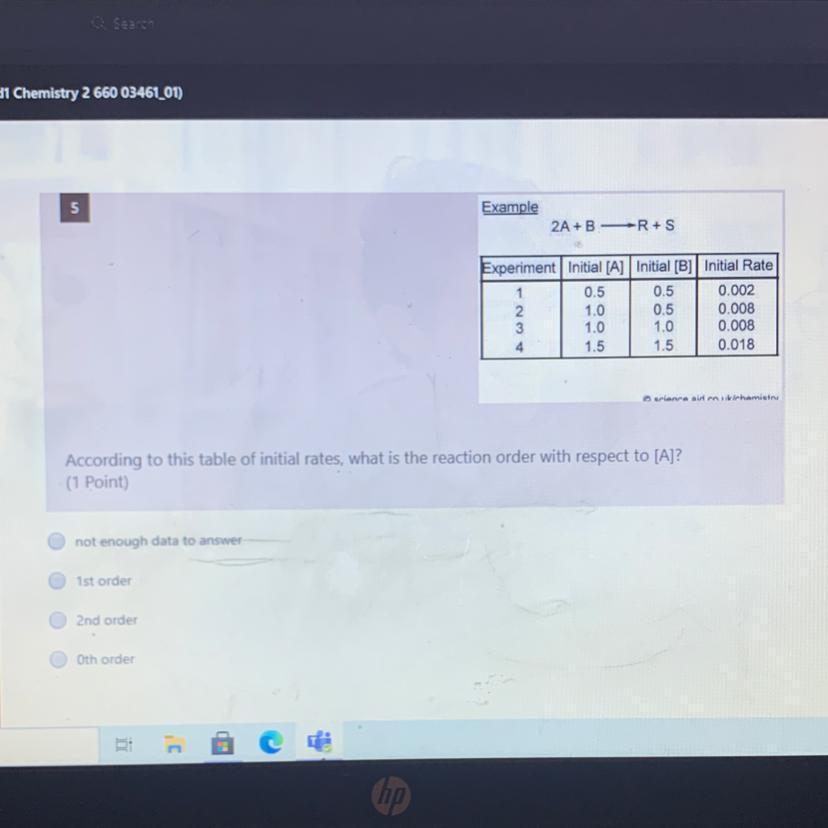
What is the order of the reaction with respect to A?
Answers
From the question, the order of reaction is second order for A
What is the order of reaction?
The rate of a second-order reaction is exactly proportional to the product of the concentrations of the two reactants or to the square of the concentration of a single reactant. Depending on the particular reaction and its stoichiometry, the rate equation for a second-order reaction can take on several shapes.
Studying reaction kinetics, figuring out reaction processes, and planning and optimizing chemical reactions all depend on understanding the order of events.
Learn more about order of reaction:https://brainly.com/question/31609774
#SPJ1
Iris's checking account pays simple interest at 4% per year. She has $180 in her account. Write a linear function to model the amount of money in her checking account at any time t.
A(t)=
Answers
The amount of money in Iris's checking account can be modeled by a linear function of the form:
y = mt + b
where y is the amount of money in the account, t is the time (measured in years), m is the rate of interest, and b is the initial amount in the account.
In this case, we have m = 0.04 (since the interest rate is 4% per year) and b = 180 (since that's the initial amount in the account). Therefore, the linear function that models the amount of money in Iris's checking account at any time t is:
y = 0.04t + 180
For example, if t = 5 (years), then the amount of money in Iris's checking account is 0.04 * 5 + 180 = 198 dollars.
Find the area under the graph of the function over the interval given. f(x)= e' [-2,2] The area is (Type an exact answer in terms of e.)
Answers
The area under the graph of the function f(x) = e^x over the interval [-2, 2] is approximately 13.77 square units.
To calculate the area under the graph of the function, we can use integration. In this case, we need to integrate the function f(x) = e^x with respect to x over the interval [-2, 2].
The definite integral represents the area under the curve between the given limits.
∫[a,b] e^x dx
Applying the integral, we have: ∫[-2,2] e^x dx
Using the rules of integration, we can evaluate this integral to find the area under the curve.
The antiderivative of e^x is e^x itself. Evaluating the integral at the upper and lower limits, we get: [e^x] from -2 to 2
Plugging in the values, we have: e^2 - e^(-2)
This is the exact answer in terms of e. To get the numerical approximation, you can substitute the value of e into the expression to get the approximate area.
To know more about area click here
brainly.com/question/13194650
#SPJ11
your classroom has triangular shaped tables. three students can sit around one table. two tables can be pushed together so that two sides are adjacent. how many students can sit around the tables in this arrangement? explain your thinking
Answers
Answer:
6
Step-by-step explanation:
If you push two triangle tables together you just multiply 3*2
The road was 3.7 miles long. After a rebuild, it was 2.6 times as long. How long was the road after rebuilding?
Answers
The road was 9.62 miles long after rebuilding.
How to calculate the length of the road ?
The road was initially 3.7 miles long
After a rebuild it was 2.6 miles as long
The new length can be calculated by multiplying the initial length which is 3.7 by 2.6
= 3.7 × 2.6
= 9.62
Hence, after the rebuild the road was 9.62 miles long
Read more on miles here
https://brainly.com/question/9243336?referrer=searchResults
#SPJ1
Find the spherical coordinate limits for the integral that calculates the volume of the solid between the sphere rho=4cos(ϕ)rho=4cos(ϕ) and the hemisphere rho=6rho=6, z≥0z≥0 . Then evaluate the integral.
Answers
To find the spherical coordinate limits for the integral, we first need to determine the bounds for ρ, θ, and ϕ.
Since the sphere and hemisphere intersect at ρ=4cos(ϕ), we can set these two equations equal to each other to find the limits for ϕ:
4cos(ϕ) = 6
ϕ = arccos(3/2)
For the limits of θ, we note that the solid is symmetric about the z-axis, so we can integrate from 0 to 2π.
Finally, for the limits of ρ, we need to find the limits for z. Since the hemisphere has equation ρ=6 and z≥0, we know that the top of the solid is at z=6. To find the bottom of the solid, we need to solve for z in the equation for the sphere:
ρ = 4cos(ϕ)
z = 4cos(ϕ)cos(θ)sin(ϕ)
Substituting ρ=4cos(ϕ) and simplifying, we get:
z = 2cos^2(ϕ)sin(θ)
Since z≥0, we have:
0 ≤ 2cos^2(ϕ)sin(θ) ≤ 6
0 ≤ sin(θ) ≤ 3/(2cos^2(ϕ))
So the limits for ρ are 4cos(ϕ) ≤ ρ ≤ 6, the limits for θ are 0 ≤ θ ≤ 2π, and the limits for ϕ are arccos(3/2) ≤ ϕ ≤ π/2.
To evaluate the integral, we use the formula for a volume in spherical coordinates:
V = ∫∫∫ ρ^2sin(ϕ) dρdθdϕ
Applying the limits we found above, we get:
V = ∫ from arccos(3/2) to π/2 ∫ from 0 to 2π ∫ from 4cos(ϕ) to 6 (ρ^2sin(ϕ)) dρdθdϕ
Evaluating the integral, we get:
V = 256π/15 - 8/3
Therefore, the volume of the solid is 256π/15 - 8/3 cubic units.
Learn more about Trigonometry here:- brainly.com/question/13729598
#SPJ11
an analysis of variance comparing three treatment conditions produces dftotal = 32. if the groups are all the same size, how many individuals are in each group?
Answers
If the total degrees of freedom (dftotal) in an analysis of variance comparing three treatment conditions is 32, the group size for each condition needs to be determined.
To determine the number of individuals in each group, we need to divide the total number of individuals (dftotal) by the number of treatment conditions (groups).
Given that dftotal = 32 and there are three treatment conditions (groups), we can divide dftotal by the number of treatment conditions to find the number of individuals in each group.
Number of individuals in each group = dftotal / number of treatment conditions
Number of individuals in each group = 32 / 3
Number of individuals in each group ≈ 10.67
Since the groups must have the same size, we need to round the result to the nearest whole number. Therefore, there are approximately 11 individuals in each group.
Learn more about variance comparing: brainly.com/question/31388424
#SPJ11
A shape is rotated 180° about the origin and then its image is reflected
in the y-axis.
Describe fully the single transformation that would have the same
result as the two transformations described above.
+
4
3
+
Х
19
2

Answers
uhm can yall give me an answer with explanationn plss

Answers
Answer:
123 degrees
Step-by-step explanation:
Angles in a quadrilateral add up to 360 degrees
so we add all the angles
114 + 80 + 43 which is 237
360 - 237 is 123
so angle x is 123 degrees
linear models have a constant growth rate (slope). what is the defining characteristic of exponential models?
Answers
The initial number of dice rolled = 1000
What is exponential modeling?
Based on an equation like where Y = deterioration, T = time, and A and B = parameters to be calculated by the regression approach based on historical data, the exponential model represents the degradation failure process.
Here,
Linear models are used when a phenomenon is changing at a constant rate whereas exponential models are used when a phenomenon is changing in a way that is quick at first, then more slowly, or slow at first and then more quickly. This is the defining characteristic of the exponential model.
(a)
dice(n) = 1000 × (−0.138629436ln)........... (1)
The initial number of dice rolled when n=0
Putting n=0 in (1),
dice(0) = 1000e(0) = 1000
Hence, the initial number of dice rolled = 1000
To learn more about exponential modeling from the given link
https://brainly.com/question/4519423
#SPJ4
Can someone help me with this example:
2(x²+y²)-5(x+y)=1
5xy-2(x+y)=20
I use this: x²+y²=a²-2b
x+y=a, xy=b
to make this example easier, but I don't get the same result as a solved example with only results.
Answers
The solutions are x = 1/9, x = 25/8, and x = 1. Substituting these values back into either equation will give the corresponding values of y.
How did we get the values?We can solve this system of equations by using elimination or substitution method.
Elimination Method:
From the second equation, we can isolate x or y in terms of the other variable:
5xy - 2(x + y) = 20
5xy - 2x - 2y = 20
5xy - 2x - 2y + 4 = 24
5xy - 2(x + 2y) + 4 = 24
5xy - 2(2 - y + 2y) + 4 = 24 (using x + y = a)
5xy - 2(2 + y) + 4 = 24
5xy - 2y = 22
y(5x - 2) = 22
y = 22/(5x - 2)
Substituting this expression for y into the first equation, we get:
2(x² + (22/(5x-2))²) - 5(x + 22/(5x-2)) = 1
Multiplying through by (5x - 2)², we get:
2(5x - 2)²(x² + 22²) - 5(5x - 2)(x(5x - 2) + 22) = (5x - 2)²
Simplifying and rearranging, we get:
9x⁴ - 100x³ + 328x² - 100x + 4 = 0
This is a quartic equation which can be solved using various methods, such as factoring, graphing, or numerical methods.
Substitution Method:
From the first equation, we can solve for y in terms of x:
2(x²+y²)-5(x+y)=1
2x² + 2y² - 5x - 5y = 1
2y² - 5y = 1 - 2x² + 5x
Using the quadratic formula, we get:
y = (5 ± sqrt(25 - 8(1-2x²+5x)))/4
y = (5 ± sqrt(8x² - 25x + 24))/4
Substituting this expression for y into the second equation, we get:
5x(5 ± sqrt(8x² - 25x + 24))/4 - 2(x + (5 ± sqrt(8x² - 25x + 24))/4) = 20
Simplifying and rearranging, we get:
(9x - 4)(8x - 25)(x - 1) = 0
Thus, the solutions are x = 1/9, x = 25/8, and x = 1. Substituting these values back into either equation will give the corresponding values of y.
learn more about substitution method: https://brainly.com/question/22340165
#SPJ1
A triangle has an angle ratio of 3:5:10. Find the measure of each angle.
Answers
Answer:
Step-by-step explanation:
let angles be 3x, 5x, 10x
3x+5x+10x=180(angle sum property)
18x=180
x=180/18
x=10
therefore, angles are 3*10=30
5*10=50
10*10=100..
The life expectancy of Timely brand watches is normally distributed with a mean of four years and a standard deviation of eight months.
a. What is the probability that a randomly selected watch will be in working condition for more than five years?
b. The company has a three year warranty period on their watches. What percentage of their watches will be in operating condition after the warranty period?
c. What is the minimum and the maximum life expectancy of the middle 95% of the watches?
d. Ninety-five percent of the watches will have a life expectancy of at least how many months?
Answers
a.The probability that a randomly selected watch will be in working condition for more than five years is approximately 6.68%. b.Approximately 93.32% of the watches will be in operating condition after the warranty period. c. The maximum life expectancy of the middle 95% of the watches is approxiamately 63.68 months. d.The range of the middle 95% of the watches is from 32.32 months to 63.68 months. The range represents 95% of the watches, it means that 5%.
a. To find the probability that a randomly selected watch will be in working condition for more than five years, we need to convert the time to the same unit as the distribution. Since the mean is given in years and the standard deviation is given in months,
we need to convert five years to months.
Mean = 4 years = 4 x 12 months = 48 months
Standard deviation = 8 months
To calculate the probability, we need to find the area under the normal distribution curve to the right of 60 months (5 years).
Using a standard normal distribution table or a calculator, we can find the z-score corresponding to 60 months:
z = (x - μ) / σ
z = (60 - 48) / 8 = 12 / 8 = 1.5
The probability can be found by looking up the z-score in the standard normal distribution table or using a calculator. From the table or calculator, we find that the probability is approximately 0.0668, or 6.68%.
b. The warranty period for Timely brand watches is three years. To find the percentage of watches that will be in operating condition after the warranty period, we need to find the probability that a randomly selected watch will last longer than three years.
We need to convert three years to months:
Warranty period = 3 years = 3 x 12 months = 36 months
We calculate the z-score:
z = (x - μ) / σ
z = (36 - 48) / 8 = -12 / 8 = -1.5
Using the standard normal distribution table or a calculator, we find the area to the left of -1.5 is approximately 0.0668. The probability that a randomly selected watch will not last longer than three years is approximately 0.0668.
To find the percentage of watches that will be in operating condition after the warranty period, we subtract this probability from 1 (since we want the complementary probability):
Percentage = 1 - 0.0668 = 0.9332 = 93.32%
c. The middle 95% of the watches represents the range within which 95% of the watches' life expectancy falls. To find the minimum and maximum life expectancy of this range, we need to determine the z-scores that correspond to the cumulative probability of 0.025 and 0.975.
For the minimum life expectancy (lower bound), we look up the z-score that corresponds to a cumulative probability of 0.025. This z-score is approximately -1.96.
z = -1.96
Using the z-score formula, we can find the corresponding value in months:
x = μ + (z x σ)
x = 48 + (-1.96 * 8) = 48 - 15.68 = 32.32
The minimum life expectancy of the middle 95% of the watches is approximately 32.32 months.
For the maximum life expectancy (upper bound), we look up the z-score that corresponds to a cumulative probability of 0.975. This z-score is also approximately 1.96.
z = 1.96
Using the z-score formula, we can find the corresponding value in months:
x = μ + (z x σ)
x = 48 + (1.96 x 8) = 48 + 15.68 = 63.68
d. Ninety-five percent of the watches refer to the range between the 2.5th and 97.5th percentiles. We already calculated the z-scores corresponding to these percentiles in part c: -1.96 and 1.96.
To find the range in months,
we convert the z-scores back:
\(x_{1}\)= μ +\(z_{1}\) x σ = 48 + (-1.96) x 8 = 32.32 months,
and \(x_{2}\)= μ + \(z_{2}\) x σ
= 48 + 1.96 x 8
= 63.68 months.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ4