c) For each positive integer value n find the greatest common divisor of n !+1 and (n+1) !+1
Answers
For each positive integer value n, the greatest common divisor (GCD) of n!+1 and (n+1)!+1 can be determined.
The GCD can be found by applying the Euclidean algorithm. We start by dividing the larger number by the smaller number and finding the remainder. Then, we divide the previous divisor by the remainder and repeat this process until we obtain a remainder of zero. The GCD is the last non-zero remainder in this process.
When we calculate the GCD of n!+1 and (n+1)!+1, we find that the remainder is 1 in each step. Hence, the GCD of n!+1 and (n+1)!+1 is always 1 for every positive integer value of n.
This means that for any positive integer n, the greatest common divisor of n!+1 and (n+1)!+1 is always 1.
To learn more about greatest common divisor: -brainly.com/question/13257989
#SPJ11
Related Questions
a tank initially contains 100 gal of a salt-water solution containing 0.05 lb of salt for each gallon of water. at time zero, pure water is poured into the tank at a rate of 3 gal per minute. simultaneously, a drain is opened at the bottom of the tank that allows the salt-water solution to leave the tank at a rate of 2 gal per minute. what will be the salt
Answers
The amount of salt in the tank after 10 minutes is 4.5 lbs.
The initial amount of salt in the tank is 100 * 0.05 = 5 lbs.
The amount of salt that leaves the tank each minute is 2 * 0.05 = 0.1 lbs.
The amount of salt that enters the tank each minute is 0 lbs.
Therefore, the net amount of salt in the tank is decreasing by 0.1 lbs per minute.
If we let t be the number of minutes, then the amount of salt in the tank at time t is given by
salt = 5 - 0.1t
To find the amount of salt in the tank after 10 minutes, we can set t = 10 and evaluate the expression. This gives us
salt = 5 - 0.1 * 10 = 4.5 lbs
Therefore, the amount of salt in the tank after 10 minutes is 4.5 lbs.
For such more question on amount:
https://brainly.com/question/25720319
#SPJ8
The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b). True False
Answers
The statement "The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b)" is False.
In a uniform distribution, the probability density function (PDF) is constant within the interval [a, b]. The height of the PDF represents the density of the probability distribution at any given point within the interval. Since the PDF is constant, the height remains the same throughout the interval.
To determine the height of the PDF, we need to consider the interval length. In a uniform distribution defined on the interval [a, b], the height of the PDF is 1/(b - a) for the PDF to integrate to 1 over the entire interval. This means that the total area under the PDF curve is equal to 1, representing the total probability within the interval [a, b].
Therefore, the correct statement is that the height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is not 1/(a - b), but rather it is a constant value necessary for the PDF to integrate to 1 over the interval, i.e., 1/(b - a).
Learn more about uniform distribution here:
https://brainly.com/question/32291215
#SPJ11
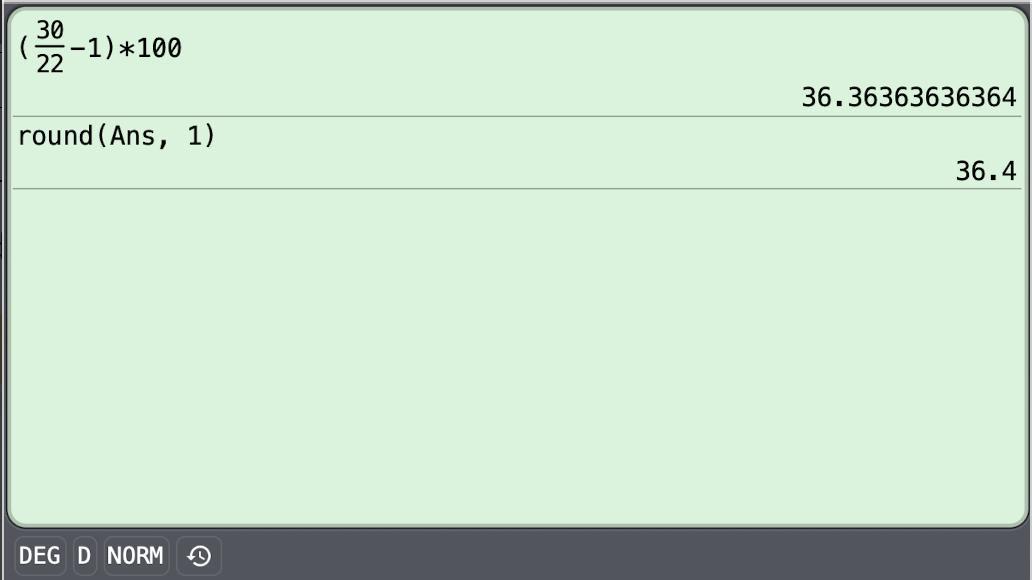
The value of a stock changes from $22 on Monday to $30 on Tuesday. Calculate the percent increase.
Answers
Answer:
36.4%
Step-by-step explanation:
You want the percentage change from $22 to $30.
Percentage changeThe percentage change is given by the formula ...
percent change = ((new value)/(old value) -1) × 100%
= (30/22 -1)(100%) ≈ 36.4%
The stock increased in value by about 36.4%.
<95141404393>
sketch the curve with the given polar equation. θ = −π/6
Answers
To sketch the curve with polar equation θ = −π/6, we need to plot all the points (r, θ) that satisfy the equation for various values of r. Since θ is fixed at −π/6, all the points will lie on a line at an angle of −π/6 to the positive x-axis.
The value of r can be positive or negative, so we will plot points both above and below the x-axis.
Since r can be any value, we will just choose a few values for illustration purposes. Let's choose r = 1, 2, −1, and −2. Then the corresponding points are:
(1, −π/6), (2, −π/6), (−1, −π/6), and (−2, −π/6)
We can plot these points on a polar coordinate system as follows:
These points lie on a line at an angle of −π/6 to the positive x-axis, as expected. Note that the sign of r determines whether the point lies above or below the x-axis.
To know more about polar coordinate refer here:
https://brainly.com/question/11657509
#SPJ11
jorje wants to estimate the percentage of people who play sports. he surveys 330 individuals and finds that 65 play sport. find the margin of error for the confidence interval for the population proportion with a 95% confidence level.
Answers
The margin of error for the confidence interval for the population proportion with a 95% confidence level is 0.000207
How to find the margin of errorfinding the percentage of 65 of 330 individuals
65 / 330 * 100 = 19.697% = 0.19697
number of samples, n = 330
standard deviation, σ is calculated from
= √{(p(1 - p)) / n}
= √{(0.197 * (1 - 19.7)) / 330}
= √{(0.197 * (0.803)) / 330}
= 0.022
Margin of error, E
= Z(0.95) * σ/√(n)
= 0.171 * 0.022/√(330)
= 0.171 * √(0.022²/330)
= 0.000207
= 0.021%
Learn more on margin of error here:
https://brainly.com/question/29326767
#SPJ1
Let f be a function such that lim h->0 ( f(2+h)-f(2) / h ) = 5. Which of the following are true?
I) f is continuous at x=2
II) f is differentiable at x=2
III) The derivative of f is coninuous at x=2
Answers
I) f is continuous at x=2
II) f is differentiable at x=2
These both f (function ) are true
The given limit can be recognized as the definition of the derivative of f at x=2. Specifically, it states that the derivative of f at x=2 is equal to 5.
Using this information, we can make the following conclusions:
I) We cannot say for sure whether f is continuous at x=2 based on the given limit alone. While a function being differentiable at a point implies that it is also continuous at that point, the converse is not necessarily true. Therefore, we would need additional information to determine whether f is continuous at x=2.
II) The given limit implies that f is differentiable at x=2, since the limit exists and is finite. Specifically, we can say that the derivative of f at x=2 exists and is equal to 5.
III) The given limit also implies that the derivative of f is continuous at x=2. This is because the limit defines a continuous function at x=2, and it is well-known that if a function is differentiable at a point, then it is also continuous at that point.
Therefore, the correct answers are II and III.
To know more about differentiable and continuous equation , refer here :
https://brainly.com/question/30039201#
#SPJ11
27°
15
Solve for b.
40°
b
b = [ ?
Round your final answer
to the nearest tenth.

Answers
10.59 is the value of the given side b.
In our case, we know that side A has a length of 15 units and is opposite angle A, which measures 27 degrees.
Using the sine rule, we can write:
b/sin(27°) = 15/sin(40°)
To find the value of b, we can rearrange the equation:
b = (15 * sin(27°)) / sin(40°)
evaluate the trigonometric functions and calculate b:
b ≈ 10.59
Therefore, using the sine rule of the triangle, we find that the value of side b is approximately 10.59 units.
Learn more about triangles here:
https://brainly.com/question/2773823
#SPJ1
what type of graph would have the title typical height jumped?
Answers
the graph that adequately fits the description would be a pictograph
because shows a symbol for a word or phrase
In triangle ABC, m∠A=23° and m∠B=33°. What is m∠C?
Answers
The measure of angle C is 122 degrees.
We have given that,
In triangle ABC, m∠A=23° and m∠B=33°
We have to determine the remaining angle of the triangle.
What is the sum of the angle of the triangle?
The sum of the angles in a triangle is 180 degrees.
Therefore we get
angle A+ angle B+ angle C= 180 degrees
23+33+angle C=180
angle C=180-56
angle C=122
Therefore the measure of angle C is 122 degrees.
To learn more about the triangle visit:
https://brainly.com/question/2217700
#SPJ1
What is the average rate of change in height over the entire 5 seconds?

Answers
Answer:“To get the average rate of change between 2 points...” To get the average rate of change between 2 points, plug in their coordinate values into the equation (y2-y1)/(x2-x1). The values come from the points (x1,y1) and (x2,y2).
Step-by-step explanation:
Please help ASAP 4-10 for Brainliest

Answers
5) 37°
6) 42°
7) 138°
8) 73°
9) 73°
10) 30°
how would you solve p-11=-14
Answers
Answer:
Step-by-step explanation:
all you would need to do is add 11 to both sides, and then you would get your answer.
What value could be added to 2/15 to make the sum greater than 1/2?A. 1/15B. 8/30C. 5/15D. 8/15
Answers
In order to find the required fraction, you can write the following inequality:
\(\frac{2}{15}+x>\frac{1}{2}\)Solve the previous inequality for x by subtracting 2/15 both sides and simplifying:
\(\begin{gathered} x>\frac{1}{2}-\frac{2}{15} \\ x>\frac{15-4}{30} \\ x>\frac{11}{30} \end{gathered}\)Then, you hava that x must be greater than 11/30.
You can notice that from the given choices, 8/15 is the only number that is greater than 11/30 (you can check it by subtracting 11/30 to 8/15, you'll get a positive number).
Hence, 8/15 is the value you can add to 2/15 to get a greater number than 1/2
The length of a table is 2 meters 50 centimeters. What is the length of the table in millimeters?

Answers
Answer:
A
Step-by-step explanation:
2 meters=2000millimeters
50 centimeters=500 millimeters
find the 6 trigonometric function values of the angle
please use either 45-45-90 triangle or 30-60-90 triangle
cos -5pi/4
sec -2pi/3
Answers
The six trigonometric functions are:
cos (-5π/4) = cos (-π/4) = -√2/2sin (-5π/4) = sin (-π/4) = -√2/2tan (-5π/4) = tan (-π/4) = 1cot (-5π/4) = cot (-π/4) = -1sec (-2π/3) = 4cosec (-2π/3) = 2/√3
Let's find the trigonometric values using the given angles:45-45-90 triangle.We know that for a 45-45-90 triangle, the sides are in a ratio of 1:1:√2 and the angles are 45°, 45°, and 90°.
Now, we are to find the trigonometric function values of the angles.cos (-5π/4) = cos (-π/4)Using unit circle, the terminal side of angle -π/4 in the fourth quadrant makes a reference angle of π/4.
The coordinates are (-√2/2, -√2/2).cos (-π/4) = -√2/2sec (-2π/3)The angle -2π/3 is in the third quadrant.
The reference angle of -2π/3 in the triangle is π/3.
Using the 30-60-90 triangle, we know that the sides are in the ratio of 1:√3:2 and the angles are 30°, 60°, and 90°.In the 30-60-90 triangle, we have: sec θ = 2/cos θsec (-2π/3) = 2/cos (π/3) = 2/1/2 = 4cos θ = 1/2
Using the coordinates on the unit circle of π/3, the adjacent side is 1/2cos θ = 1/2sin θ = √3/2tan θ = sin θ/cos θ = √3cot θ = 1/tan θ = 1/√3cosec θ = 1/sin θ = 2/√3.
The six trigonometric functions are:
cos (-5π/4) = cos (-π/4) = -√2/2sin (-5π/4) = sin (-π/4) = -√2/2tan (-5π/4) = tan (-π/4) = 1cot (-5π/4) = cot (-π/4) = -1sec (-2π/3) = 4cosec (-2π/3) = 2/√3
For more question on trigonometric functions
https://brainly.com/question/25618616
#SPJ8
2 x 4 when is the next seson on tolet bound hanako kun comming out?
Answers
Answer:
8.. the release date of Toilet Bound Hanako Kun season 2 will be spring 2021
Step-by-step explanation:
WE STILL DON'T KNOW... BUT READ THE MANGA IS FASTER THAN WAITING FOR SEASON 2
What is an equivalent form of the function f(x) = x^2 -8x+15 that reveals the zeros of the function?
Answers
Step-by-step explanation:
The form of a polynomial that reveals the zeroes is factors form.
\(y = a(x - r)(x - q)\)
where r and q are the zeroes of the function.
So we need to unFOiL this method
We need two number that multiply to 15, but add to -8
So let find two numbers that
The factors of 15 are 1,3,5,15,-1,-3,-5,-15
Since our middle term is negative and our last term is positive, we have two negative roots.
That would just turn out to be -3, and -5
So we get
\(y = (x + 3)(x + 5)\)
Which reveals the zeroes as -3 and -5
Solve the following inequality, graph the solution, and write
the solution in interval notation.
3x + 7 ≤ 13x + 7 ≤ 1 AND 2x + 3≥ − 5
Answers
First, let's solve the inequality 3x + 7 ≤ 13x + 7 ≤ 1:3x + 7 ≤ 13x + 7 Subtract 13x from both sides. -10x + 7 ≤ 7 Subtract 7 from both sides. -10x ≤ 0
Divide both sides by -10, remembering to reverse the inequality .x ≥ 0. Now let's solve the inequality 2x + 3 ≥ -5:2x + 3 ≥ -5
Subtract 3 from both sides. 2x ≥ -8 Divide both sides by 2. x ≥ -4.Using both inequalities, the solution is x ≥ -4 and x ≥ 0. This is because both inequalities must be satisfied at the same time. In interval notation, the solution is (-∞, ∞), meaning that x can be any number from negative infinity to positive infinity.
This is because the solution includes all real numbers greater than or equal to -4 and all real numbers greater than or equal to 0.
To know more about inequality refer here:
https://brainly.com/question/20383699
#SPJ11
For each of the following equations,give the centre and radius of the circle.
a)x^2 + y^2 = 25 b) x^2 + y^2= 1
d) (x - 5)^2 + (y-3)^2 = 81 e) (x+2)^2 + (y-1)^2 = 9
g) (x + 1)^2 + (y + 3)^2 = 49 h) x^2+ y^2 = 6.25
Answers
Answer:
a) Center is (0,0) and radius r = 5
b) Center is (0,0) and radius r = 1
d) Center is (5,3) and radius r = 9
e Center is (-2,1) and radius r = 3
g) Center is (-1,-3) and radius r = 7
h) Center is (0,0) and radius r = 2.5
Step-by-step explanation:
a)
Given circle x² + y² = 25
The standard form of circle equation is
( x-h)² +(y-0)² = r²
Center is (0,0) and radius r = 5
b)
Given circle x² + y² = 1
The standard form of circle equation is
( x-h)² +(y-0)² = r²
Center is (0,0) and radius r = 1
d)
Given circle (x-5)² + (y-3)² = 81
The standard form of circle equation is
( x-h)² +(y-0)² = r²
(x-5)² + (y-3)² = 9²
Center is (5,3) and radius r = 9
e)
Given circle (x+2)² + (y+1)² = 9
The standard form of circle equation is
( x-h)² +(y-0)² = r²
(x+2)² + (y+1)² = 3²
Center is (-2,-1) and radius r = 3
g)
Given circle (x+1)² + (y+3)² = 49
The standard form of circle equation is
( x-h)² +(y-0)² = r²
(x+1)² + (y+3)² = 7²
Center is (-1,-3) and radius r = 7
h)
Given circle x² + y² = 6.25
The standard form of circle equation is
( x-h)² +(y-0)² = r²
Given circle x² + y² = (2.5)²
Center is (0,0) and radius r = 2.5
A given line has the equation 3x - 5y= 20 . Which of the following equations represents the line perpendicular to the given line and passes through the point (-6, 4)?
A.) 5x + 3y = 18
B.) y = -5/3x + 10
C.) y = -5/3x - 6
D.) 5x - 3y = -18
E.) y = -3/5x + 0.4
Answers
Answer:
C
Step-by-step explanation:
the slope of a line is anyways the factor of x.
the slope of a perpendicular line is just the upside-down fraction of the original line slope, and its sign is flipped.
3x - 5y = 20
5y = 3x - 20
y = (3/5 × x) - 4
3/5 turns into -5/3
and the point coordinates must satisfy the line equation :
4 = (-5/3 × -6) - 6
4 = 30/3 - 6 = 10 - 6 = 4
correct.
so, C is the correct solution.
At the beginning of 2005 there were 670 deer living in a nature reserve. The population is declining by x% each year and after 4 years has reduced to 557. Find the value of x. Give your answer correct to 2 decimal places.
Answers
The annual rate of decline is 5.3%.
What is exponential ?
Exponential refers to a mathematical function where the variable is in the exponent. Exponential functions have the general form:
\(f(x) = a^{x}\)
here "a" is a constant called the base, and "x" is the variable. When the base "a" is a positive number greater than 1, the function grows exponentially as "x" increases. When the base "a" is a number between 0 and 1, the function decays exponentially as "x" increases.
We can start by using the formula for exponential decay:
\(N(t) = N0 * (1 - r)^{t}\)
where N(t) is the population after t years, N0 is the initial population, r is the annual rate of decay (as a decimal), and t is the time in years.
We are given that the initial population is 670, so N0 = 670. After 4 years, the population has reduced to 557, so N(4) = 557. We can plug these values into the formula and solve for r:
\(557 = 670 * (1 - r)^{4}\)
\((557/670)^{1/4} = 1 - r\)
\(0.947 = 1 - r\)
\(r = 0.053\)
So the annual rate of decline is 5.3%.
To learn more about exponential visit the link:
https://brainly.com/question/11975096
#SPJ1
the procedure for identifying or indicating the value of cases on a variable
Answers
Specific procedures and techniques for coding variables may vary depending on the context, research area, or data analysis software used.
What is a Variable?
A variable is a quantity that can change in the context of a mathematical problem or experiment. We usually use one letter to represent a variable. The letters x, y, and z are common general symbols used for variables.
The procedure for identifying or indicating the value of cases on a variable is commonly known as data coding or data labeling. It involves assigning specific numerical or categorical values to represent different categories or levels of a variable.
Here is the general procedure for encoding variables:
Define the variable: Start by clearly defining the variable you want to code. Understand its nature (eg nominal, ordinal, interval or ratio) and the categories or levels it covers.
Determine the encoding scheme: Decide on the encoding scheme you will use to represent the variable. For nominal variables (categories without their own order), you can assign numbers or labels to each category. For ordinal variables (categories with a meaningful order), you can assign numbers or labels that reflect the order. For interval or ratio variables, the numerical values themselves can indicate the value of the variable.
Assign Codes: Assign specific codes or labels to represent each category or level of the variable. These codes can be numbers, letters, or any other symbol you choose. Make sure the codes are unique and do not overlap.
Apply Coding: Apply assigned codes to matching cases or observations in your dataset. Depending on the software or tool you are using, there are different ways to do this. You can manually enter codes, use syntax or programming commands, or use data transformation functions.
Verify your coding: Double-check your coding to ensure accuracy. Review a sample of the coded cases to ensure they match the intended coding scheme. This step is essential to avoid errors and inconsistencies in your data.
It is important to note that specific procedures and techniques for coding variables may vary depending on the context, research area, or data analysis software used.
To learn more about Variable from the given link
https://brainly.in/question/47865408
#SPJ4
Jason jumped off of a 80 meter tall cliff at a velocity of 7 m/s into the ocean in Acapulco while vacationing with
some friends. How long will it take Jason to reach the ocean in seconds, rounded to the nearest hundredth?
7/1
Answers
Answer:
11.43 seconds
Step-by-step explanation:
80/7 = 11.428 = 11.43( nearest hundredth)
you have a fair coin and want to calculate the probability that if you flip the coin 20 times, you will get at least 14 heads. what is the probability that you will get heads more than 14 times?
Answers
The probability of getting at least 14 heads when flipping a fair coin 20 times is 0.25.
This can be calculated using the binomial distribution formula which states that the probability of obtaining exactly x successes in n trials is given by
P(x) = (n choose x) * p^x * (1-p)^(n-x),
where n is the total number of trials, p is the probability of success, and x is the number of successes.
For this problem, n=20, p=0.5, and x=14, so the probability of getting at least 14 heads is P(x) = (20 choose 14) * 0.5^14 * 0.5^6 = 0.25.
Learn more about probability:
https://brainly.com/question/13604758
#SPJ4
can you guys help me with this

Answers
The number line for the set of jump distances to make a new record.
Option B is the correct answer.
What is a number line?It is the representation of numbers in real order.
The difference between the consecutive numbers in a number line is always positive.
We have,
The school record in the long jump = 518 cm
Now,
To make a new record the set of jump distances should be greater than 518 cm.
To represent the set of jump distances on a number line we can not have a black dot on 513 on the number line.
The dot should be an open dot.
Thus,
Option B is the number line for the set of jump distances to make a new record.
Learn more about number line here:
https://brainly.com/question/13425491
#SPJ1
4x-22<-6 on a number line
Answers
By answering the above question, we may state that Shade the region to line the left of the open circle, since x is less than 4.
what is a line?A line is a geometric object that is infinitely long and has no width, depth, or curvature. A line, which can also exist in two-, three-, and more-dimensional spaces, is therefore a one-dimensional object. A line is often used to refer to a line segment with two points as its endpoints. A line is a flat, one-dimensional object that may extend indefinitely in both directions and has no thickness. The terms "straight line" or "old correct line" are sometimes used to describe a line that has no "wobble" anywhere along its length.
plot the inequality 4x-22<-6 on a number line,
4x - 22 + 22 < -6 + 22
4x < 16
4x/4 < 16/4
x < 4
Plot an open circle at 4 on the number line to indicate that x is not included in the solution set.
Shade the region to the left of the open circle, since x is less than 4.
The resulting graph should look like this:
○----------------->
| | | | | | |
-∞ -5 -4 -3 -2 -1 0 1 2 3 4 5 6
To know more about line visit:
https://brainly.com/question/2696693
#SPJ1
the banana is 8 inches long how many 0.4 inch slices can be cut from the banana
Answers
Answer:20
Step-by-step explanation:
what digit is in the hundredths place 132.054
Answers
Answer:
5
Step-by-step explanation:
0 is 10ths 5 is 100ths
Find the value of x. * 66 (3x + 21) 57°A)12B)15C)57D)10
Answers
We have a triangle with angles: 66 deg, 57 deg and (3x+21).
We have to solve for x.
We know that the sum of the interior angles of a triangles is 180 degrees.
Then, we can write and solve for x as:
\(\begin{gathered} 66+57+(3x+21)=180 \\ 3x+21=180-57-66 \\ 3x+21=57 \\ 3x=57-21 \\ 3x=36 \\ x=\frac{36}{3} \\ x=12 \end{gathered}\)The value of x is 12.
Answer: A) 12
Consider a relation R(A,B,C,D,E) with the following dependencies: {AB-> C, CD -> E, DE -> B} Is AB a candidate key of this relation? If not, is ABD? Explain your answer. No. The closure of AB does not give you all of the attributes of the relation.
If not, is ABD? Explain your answer. A -> A
B -> B
C -> C
D -> D
E -> E
AB -> ABC
AC -> AC
AD -> AD
AE -> AE
BC -> BC
BD -> BD
BE -> BE
CD -> BCDE
CE -> CE
DE -> BDE
ABD -> ABCDE
Yes, ABD is a candidate key. No subset of its attributes is a key.