Warm-Up
Plot the vertex and the axis of symmetry of this function on the provided graph
f(x) = (x + 2)2 - 6
Use the drawing tools to form the correct answers on the graph.
Drawing Tools

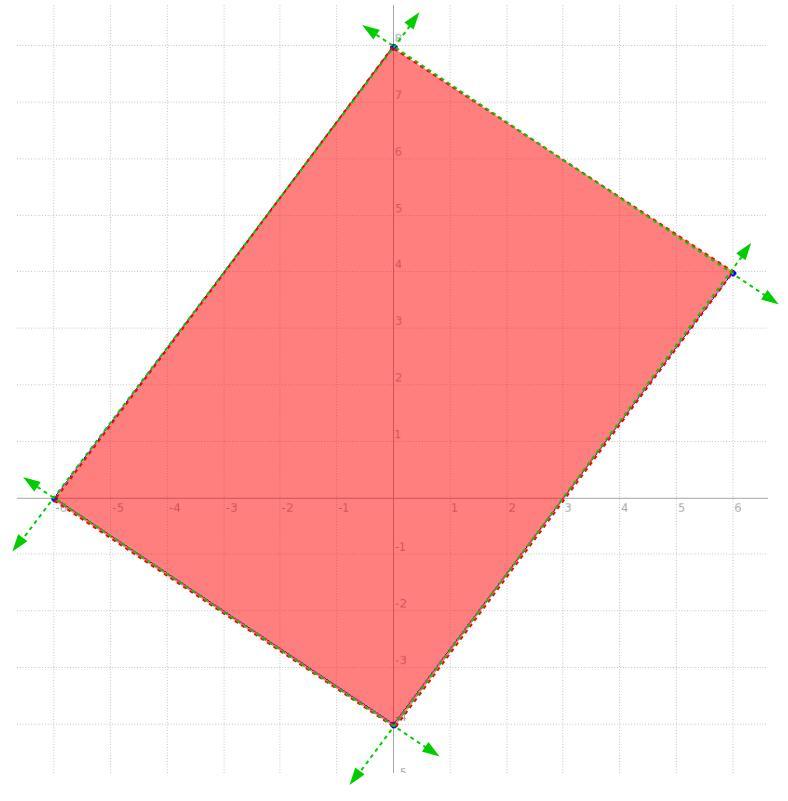
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.

we have a line passing through (-6,0) and (0,8), side one

we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two

we have a line passing through (0,-4) and (6,4), side three

now, side four is simply the line connecting one and three.

the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?

well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.

\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)

\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)

\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)

\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)

now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to  (-3 , 4).  Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.

now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality

\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)

Sets of values that could be the intensities of Amber’s exercise during the fourth, fifth, and sixth visits are -

66%, 69%, 72%

63%, 65%, 67%

What is intensity?

In physics, the power transferred per unit area is known as the intensity or flux of radiant energy, where the area is measured on a plane perpendicular to the direction of the energy's propagation.

The program recommends a pattern of constant intensity for 3 visits, increasing intensity over 3 visits, and then decreasing intensity for 3 visits before restarting the pattern.

Let's call the starting intensity level "x".

Then the intensity levels for the first 3 visits are all equal to x, the intensity levels for the next 3 visits are increasing, and the intensity levels for the following 3 visits are decreasing.

To determine which sets of values could be the intensities of Amber's exercise during the fourth, fifth, and sixth visits, we need to follow the pattern.

If the intensity level for the first 3 visits is x, then the intensity levels for the next 3 visits are x plus some value y, and the intensity levels for the following 3 visits are x plus some value z, where y and z are positive.

If we assume that the initial intensity level x is some value between 60% and 70%, then we can eliminate the last option of 67%, 72%, and 77% because the initial intensity level is too high.

Now let's check the remaining options -

63%, 63%, 63%: This set of values corresponds to a pattern of constant intensity for all 9 visits, which is not consistent with the program's recommendation.

Therefore, this option is not valid.

66%, 69%, 72%: This set of values corresponds to a pattern of increasing intensity over 3 visits, which is consistent with the program's recommendation.

Therefore, this option is valid.

66%, 62%, 58%: This set of values corresponds to a pattern of decreasing intensity over 3 visits, which is not consistent with the program's recommendation.

Therefore, this option is not valid.

63%, 65%, 67%: This set of values corresponds to a pattern of increasing intensity followed by decreasing intensity, which is consistent with the program's recommendation.

Therefore, this option is valid.

Therefore, there are only two valid options -

66%, 69%, 72%

63%, 65%, 67%

To learn more about intensity from the given link

https://brainly.com/question/28145811

#SPJ1

Answer:

There is two simple equations one where you take out x as a comman factor and y as a common factor

Step-by-step explanation:

x(2x - 5y+ 2y squared)

Y(2x squared - 5x + 2y)

Sorry I don't know how to do the sqaure thingy but that's how you find two separate equations

9514 1404 393

Answer:

  24 ft

Step-by-step explanation:

Adding 8 ft to the length adds 2 ft to the width. The largest pool is 8 ft longer than the next-largest, so is expected to be 2 ft wider.

  22 ft + 2 ft = 24 ft

The Coffeetable pool is expected to be 24 ft wide.

Answer:

24

Step-by-step explanation:

Because the wideness of the pool increase by 2 feet wide whenever the size of the increases

Answer:

12% I’m not sureeee

Step-by-step explanation:

Answer:

B and C

Explanation:

Only plant cells have a cell wall and chloroplast

Answer:   \(\;\;\frac{1}{6} , \;\; 0.16667,\;\; \text{or about}\;\;17\%\)

Step-by-step explanation:

   A regular dice has 6 sides, and only one of those sides side has a six.

        We write probability as;

   \(\displaystyle \frac{\text{wanted outcomes}}{\text{possible outcomes}} = \frac{\text{number of times six is on the dice}}{\text{number of numberss on the dice}} =\frac{1}{6}\)

Hi, there!

 _______

\(\boxed{\boxed{\sf{Probability=\dfrac{Favorable \ Outcomes}{Total \ Outcomes}}}}\)

Here,

» Favourable Outcome(s) -> getting a 6 on a die (1 outcome),  because only one side of a die has a six on it

» Total Outcomes -> 6 (you can only get 1, 2, 3, 4, 5, 6 if you roll one die)

So,

\(\sf{Probability_{(6)}=\dfrac{1}{6}}\)

Hope the answer - and explanation - made sense to you,

happy studying!!

                                                                                                        \(\tiny\textit{frozen \ melody}\)

Answer:

The saying money breeds money means that with money, you have the possibility to create more money. Simple interest is the idea that you have something, and you obtain a percentage of that every designated time period. That being said, simple interest = money breeds money

Answer: 45

Step-by-step explanation:

The total profit in all was \(1040-900=\$ 140\).

The total profit per pizza was \((0.50)(8)=\$4\).

This means they sold \(\frac{140}{4}=35\) pizzas.

Adding this to the 10 pizzas held back, there were \(35+10=45\) pizzas in the original order.

Answer:

15 miles

Step-by-step explanation:

The Pythagorean theorem states that \(a^2+b^2=c^2\) where a and b are the two legs (the sides of the triangle that are adjacent to the right angle) and c is the hypotenuse (the longest side). This only applies to right triangles.

Plug 12 mi and 9 mi into \(a^2+b^2=c^2\) as a and b.

\(a^2+b^2=c^2\\12^2+9^2=c^2\\144+81=c^2\\225=c^2\)

Take the square root of both sides

\(15=c\)

Therefore, the length of the hypotenuse is 15 miles.

I hope this helps!

Let's work on the following equation

when m = 0,

... n = 5

therefore, one of the points of this line is (0, 5)

let's find a second point

when n = 0, then

... m = - 7.5

therefore, the second point for this line is (-7.5 , 0)

using this two points we can graph the system

so, the graph for the equation n = 2/3 m + 5 will be:

The second equation is:

Again, let's find two points tha belong to the line

when m = 0, then

... n = 5

So, our first point for this equation, is (0. 5)

for our second point, when n = 0, then

... m = -7.5

Therefore, the second point is (-7.5 , 0)

This equation can be represented by the following graph:

Finally, we need to solve the system of equations

substite n from eq1 to eq2

simplify

Since we obtained -45 = -45, the system of equations has infinite solutions

Answer:

There are a total of 20 presents, and 3 of them contain gems. Therefore, there are 20 - 3 = 17 presents that do not contain gems.

The probability of randomly selecting a present that does not contain a gem is 17/20 = 0.85 or 85%.

hope it helps you...

The equation for the given situation is 7x+6=55 and the solution is x=7. Therefore, option A is the correct answer.

The given statement is six more than the product of seven and a number is 55.

In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =.

Let the unknown number be x.

Now, six more than the product of seven and a number is 55

7x+6=55

Solve the obtained equation.

That is, 7x=55-6

⇒7x=49

⇒x=7

The equation for the given situation is 7x+6=55 and the solution is x=7. Therefore, option A is the correct answer.

To learn more about an equation visit:

https://brainly.com/question/14686792.

#SPJ5

Answer:

C) A boarding kennel...

Step-by-step explanation:

C) A boarding kennel...

Answer:

Step-by-step explanation:

Both parts of the ratio can be divided by 9

81/9 = 9

72/9 = 8

The ratio is 9:8

54/48 is also 9:8

54 / 6 = 9

48/6 = 8

The ratio is 9:8

63:56 is also an answer

63 / 7 = 9

56/7 = 8

The ratio  is 9:8

The others don't work. You can just look at them to see why.

The figure labelled JKLM is a kite and the length ML is equal to 11.

A kite is a quadrilateral that have two pairs of equal length of sides and these sides are adjacent to each other. It can be viewed as a pair of congruent triangles with a common base.

The line JM bisects the kite into two congruent triangles, and thus;

the lengths ML and MK are equal.

ML = 5x - 4 and MK = 2x + 5 so;

5x - 4 = 2x + 5 {collect like terms}

5x - 2x = 5 + 4

3x = 9

x = 9/3 {divide through by 3}

x = 3

we substitute 3 for x;

ML = 5(3) - 4

ML = 15 - 4

ML = 11

Therefore, the value of length ML for the kite is equal to 11.

Know more about kite here:https://brainly.com/question/20597161

#SPJ1

The percentage population increase from 2001 to 2011 is 50%.

To calculate the percentage population increase from 2001 to 2011, you need the population figures for both years. Let's assume the population in 2001 was 100,000 and in 2011 it was 150,000.

The formula to calculate the percentage increase is:

Percentage Increase = ((New Value - Old Value) / Old Value) * 100

Plugging in the values:

Percentage Increase = ((150,000 - 100,000) / 100,000) * 100 = (50,000 / 100,000) * 100 = 0.5 * 100 = 50%

Therefore, the percentage population increase from 2001 to 2011 is 50%.

Please note that the actual population figures for the respective years need to be used in the calculation to obtain an accurate result. The example above is for illustrative purposes.

For more such questions on percentage.

https://brainly.com/question/24877689

#SPJ8

Step-by-step explanation:

A car is on a slope of 10degree above the horizontal . a force 1000N is applied to the car up the line of the slope. the car has amass of 500 kg . what is the acceleration of the car

The three Pythagorean trigonometric identities, which I’m sure one can find in any Algebra-Trigonometry textbook, are as follows:

sin² θ + cos² θ = 1

tan² θ + 1 = sec² θ

1 + cot² θ = csc² θ

where angle θ is any angle in standard position in the xy-plane.

Consistent with the definition of an identity, the above identities are true for all values of the variable, in this case angle θ, for which the functions involved are defined.

The Pythagorean Identities are so named because they are ultimately derived from a utilization of the Pythagorean Theorem, i.e., c² = a² + b², where c is the length of the hypotenuse of a right triangle and a and b are the lengths of the other two sides.

This derivation can be easily seen when considering the special case of the unit circle (r = 1). For any angle θ in standard position in the xy-plane and whose terminal side intersects the unit circle at the point (x, y), that is a distance r = 1 from the origin, we can construct a right triangle with hypotenuse c = r, with height a = y and with base b = x so that:

c² = a² + b² becomes:

r² = y² + x² = 1²

y² + x² = 1

We also know from our study of the unit circle that x = r(cos θ) = (1)(cos θ) = cos θ and y = r(sin θ) = (1)(sin θ) = sin θ; therefore, substituting, we get:

(sin θ)² + (cos θ)² = 1

1.) sin² θ + cos² θ = 1 which is the first Pythagorean Identity.

Now, if we divide through equation 1.) by cos² θ, we get the second Pythagorean Identity as follows:

(sin² θ + cos² θ)/cos² θ = 1/cos² θ

(sin² θ/cos² θ) + (cos² θ/cos² θ) = 1/cos² θ

(sin θ/cos θ)² + 1 = (1/cos θ)²

(tan θ)² + 1 = (sec θ)²

2.) tan² θ + 1 = sec² θ

Now, if we divide through equation 1.) by sin² θ, we get the third Pythagorean Identity as follows:

(sin² θ + cos² θ)/sin² θ = 1/sin² θ

(sin² θ/sin² θ) + (cos² θ/sin² θ) = 1/sin² θ

1 + (cos θ/sin θ)² = (1/sin θ)²

1 + (cot θ)² = (csc θ)²

3.) 1 + cot² θ = csc² θ

To solve this problem, we need to use vector addition to find the resultant velocity of Julia.

Let's assume that the east direction is the positive x-axis and the south direction is the negative y-axis.

The velocity of Julia in still water is 8 km/hr in the positive x-axis direction.

The velocity of the river is 3 km/hr in the negative y-axis direction.

To find the magnitude and direction of Julia's velocity, we need to find the resultant velocity vector, which is the vector sum of her velocity in still water and the velocity of the river.

Using the Pythagorean theorem, the magnitude of the resultant velocity can be calculated as:

|V| = √(Vx² + Vy²)

where Vx is the x-component of the resultant velocity and is equal to Julia's velocity in still water, and Vy is the y-component of the resultant velocity and is equal to the velocity of the river.

Vx = 8 km/hr

Vy = -3 km/hr

|V| = √(8² + (-3)²) = √(64 + 9) = √73 km/hr

The direction of the resultant velocity can be calculated as:

θ = tan⁻¹(Vy / Vx)

θ = tan⁻¹(-3 / 8) = -20.56°

The negative sign indicates that the resultant velocity vector makes an angle of 20.56° below the positive x-axis (east direction).

Therefore, the magnitude of Julia's velocity is approximately 8.54 km/hr, and the direction of her velocity is 20.56° below the positive x-axis (east direction).

Answer:

1 2/3

Step-by-step explanation:

8/9 + 7/9

Since the denominators are the same, we can add terms

15/9

This is an improper fraction so we can simplify

9/9 + 6/9

1 + 2/3

1 2/3

the Answer

5/3

or

1 2/3

Square Area = side x side = 3x3 = 9

Rectangle Area = side x side= 7x3= 21

9 + 21 = 30 square inches

Answer:

30 square inches

Step-by-step explanation:

   \(\boxed{\text{\bf Area of rectangle = length *width}}\)

Rectangle1:

     Area = 6 * 3

              = 18 square inches

Rectangle2:

Area = 4 * 3

          = 12 square inches

Area of the figure = area of rectangle1 + area of rectangle2

                             = 18 + 12

                             = 30 square inches

Answer:

Step-by-step explanation:

17(7x−3) =1

Divide both sides by 17

7x - 3 = 1/17

Collect like terms

7x = 1/17 + 3

x = (1/17 + 3) /7

x = 52/17 ÷ 7

x = 52/17 × 1/7

x = 52/119

Answer:

-6, -5, -2, 9, 10

Step-by-step explanation:

Answer:

-6,-5,-2,9,11

Answer: y=0.25

Step-by-step explanation: 1.2 / 4.8 = 0.25

Answer:

its c

Step-by-step explanation:

Answer:

B (Frozen foods can be a good substitute for fresh foods.)

Step-by-step explanation:

because in the text: cherish the season," is her motto. If kids want something out of season, it's OK to buy frozen. Then steel yourself for some complaining and use the opportunity to convey a larger lesson. so i think its be because there kind of saying that its ok to have frozen food in the winter because its expensive to get fresh food in winter.

According to the quantity theory of money, changes in the money supply will lead directly to changes in the price level if velocity and real GDP are unaffected by the change in the money supply.Velocity can change over time, and changes in velocity may be caused by various factors.

For example, changes in velocity can be caused by shifts in payment practices, changes in the use of credit, changes in the availability of bank deposits or cash, or shifts in demand patterns.Changes in velocity may be related to changes in the money supply.

For example, if the money supply increases, the demand for money may increase, causing the velocity of money to decrease. Conversely, if the money supply decreases, the demand for money may decrease, causing the velocity of money to increase.

For more question on velocity

https://brainly.com/question/25749514

#SPJ8

The negations of the given statements with the application of De Morgan's law and/or conditional law.

a) ∃x (¬P(x) ∨ ¬R(x))

De Morgan's law:

∃y ∀z(¬P(y) ∧ ¬Q(z))

b) ∃y ∀z(¬P(y) ∧ ¬Q(z))

The double negation:

∃y ¬∃z(P(y) ∨ Q(z))

c) ¬∃x (P(x) ∨ (∀z (¬R(z)) → (∀z ¬Q(z))))

The conditional law:

¬∃x (P(x) ∨ (∀z (¬R(z)) → (∀z ¬Q(z))))

Let's form the negation of the given statements and apply De Morgan's law and/or conditional law, when applicable:

a) ∀x (P(x) ∧ R(x))

The negation of this statement is:

∃x ¬(P(x) ∧ R(x))

Now let's apply De Morgan's law:

∃x (¬P(x) ∨ ¬R(x))

b) ∀y∃z(¬P(y) → Q(z))

The negation of this statement is:

∃y ¬∃z(¬P(y) → Q(z))

Using the conditional law, we can rewrite the negation as:

∃y ¬∃z(¬¬P(y) ∨ Q(z))

c) ∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))

The negation of this statement is:

¬∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))

Using the conditional law, we can rewrite the negation as:

¬∃x (P(x) ∨ (∀z (R(z) ∨ ¬Q(z))))

Applying De Morgan's law:

¬∃x (P(x) ∨ (∀z ¬(¬R(z) ∧ Q(z))))

Simplifying the double negation:

¬∃x (P(x) ∨ (∀z ¬(R(z) ∧ Q(z))))

Using De Morgan's law again:

¬∃x (P(x) ∨ (∀z (¬R(z) ∨ ¬Q(z))))

For similar questions on De Morgan's law

https://brainly.com/question/28735989

#SPJ8

Answer:

R

Step-by-step explanation: