If Kilah were running on a track that was 3/4 of a mile long, how many laps would it take
run 9 miles?
Answers
Answer: 6.75 or 7 laps
Related Questions
In 2001 , Americans consumed an average of 18.1 gallons of bottled water per person. In 2011 , that number climbed to 30.5 gallons per person.
a. Find a linear function that describes the gallons of bottled water consumed per person as a function of t. Let t denote the number of years since 2001 . B(t)=
b. What is the slope of the corresponding line, and what does it signify? The slope is and signifies Select an answer
c. What is the y-intercept of the corresponding line, and what does it signify? The y-intercept is (0,) and signifies
Answers
a. B(t) = 1.24t + 18.1;
b. Slope is 1.24, signifies increase in bottled water consumption per person every year;
c. Y-intercept is 18.1, signifies initial bottled water consumption per person in 2001.
a. To find the linear function, we need to first find the slope and y-intercept.
We can use the two given data points: (0, 18.1) and (10, 30.5).
Using the slope formula, we get:
slope = (30.5 - 18.1) / (10 - 0)
= 1.24
Now we can use the point-slope form of a line to find the equation:
y - 18.1 = 1.24(t - 0)
y = 1.24t + 18.1
So the function is B(t) = 1.24t + 18.1.
b. The slope of the line is 1.24, which signifies that for every year since 2001, there is an increase in 1.24 gallons of bottled water consumed per person.
c. The y-intercept of the line is 18.1, which signifies the initial amount of bottled water consumed per person in 2001.
To learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ4
the frosty ice-cream shop sells sundaes for $2 and banana splits for $3. on a hot summer day, the shop sold 8 more sundaes than banana splits and made $156. how many of each did they sell?
Answers
Therefore, the Frosty ice cream shop sold 28 banana splits and 28+8=36 sundaes.
Let's assume that the Frosty ice cream shop sold "x" banana splits. If they sold 8 more sundaes than banana splits, then they must have sold "x+8" sundaes.
Additionally, since the sundaes cost $2 and banana splits cost $3, the total revenue from selling "x" banana splits is $3x and the total revenue from selling "x+8" sundaes is $2(x+8).
So, we can write the equation:
$3x + $2(x+8) = $156
Simplifying and solving for "x", we get:
$5x + $16 = $156$5x = $140x = 28
Therefore, the Frosty ice cream shop sold 28 banana splits and 28+8=36 sundaes.
To know more about summer day visit:
https://brainly.com/question/9236850
#SPJ11
Tina is selling tickets for a fundraiser.
She wants to sell more than $300 worth
of tickets. The inequality 12t> 300 can
be used to determine the number of
tickets, t, she must sell in order to meet
her goal. Which number line represents
the solution to this inequality? (6. 9B |
6. 1A, 6. 1B, 6. 10, 6. 1F)
10
20
30
B
to
10
20
30
+
С
+o
+
10
20
30
D
+
10
O
20
30
Answers
The number line that represents the solution to this inequality is 6.10, with an open circle at 25 and shading to the right.
To solve the inequality 12t > 300, we need to isolate t on one side of the inequality. We can do this by dividing both sides by 12:
12t/12 > 300/12
t > 25
This means that Tina must sell more than 25 tickets in order to meet her goal of selling more than $300 worth of tickets.
To represent this solution on a number line, we can start by plotting a point at 25. Since the inequality is greater than (>) and not greater than or equal to (≥), we use an open circle at 25.
Then, we need to shade the area to the right of 25 to represent all the possible values of t that satisfy the inequality. This is because any value of t greater than 25 will make 12t greater than 300.
Out of the answer choices given, the number line that represents the solution to this inequality is 6.10, with an open circle at 25 and shading to the right.
To know more about inequality, refer to the link below:
https://brainly.com/question/22010462#
#SPJ11
write .48 as a fraction in simplest form
Answers
Answer:
12/25
Step-by-step explanation:
0.48 is read as "forty-eight hundredths," so we can write it as a fraction as
48/100.
Since both 48 and 100 have a common factor, we can reduce the fraction.
48 and 100 are both divisible by 4.
48/100 = 12/25
There are no common factors of 12 and 25, so 12/25 is the answer.
Answer:
12/25
Step-by-step explanation:
48/100 Divide by 2
24/50 Divide by 2 again
12/25 Can not be further simplified.
I hoped this helped you
Part A
Joseph runs 2 miles on Monday. Each day after that, he runs the same 1 mile route every morning. His goal is to run at least 6 miles
by the end of the week. Which inequality represents the least number of days after Monday that Joseph needs to run to reach his goal?
Answers
Sine he runs 2 miles on Monday, we already have a +2.
Then, he runs by a constant rate of 1, which is the constant rate of change per day.
Let x represent the number of days he runs and y the total amount of miles he runs. Now, the equation is y = x + 2
However, he needs to run at least 6 miles. At least means greater than or equal to. The values for y can be greater than 6, or equal to 6.
y ≥ 6
y = x + 2
Now substitute x + 2 for y.
x + 2 ≥ 6
Subtract 2.
x ≥ 4
This is the inequality. He has to run for at least 4 days.
usage patterns are a variable used in blank______ segmentation.
Answers
Answer:
usage patterns are a variable used in market segmentation.
Step-by-step explanation:
Usage patterns are a variable used in behavioral segmentation.
Behavioral segmentation is a marketing strategy that divides a market into different segments based on consumer behavior, specifically their patterns of product usage, buying habits, and decision-making processes. This segmentation approach recognizes that customers with similar behavioral characteristics are likely to exhibit similar preferences and respond in a similar manner to marketing initiatives.
Usage patterns, as a variable, help marketers understand and classify customers based on how they interact with a product or service. This can include factors such as the frequency of product usage, the amount of product used, the timing of purchases, brand loyalty, product benefits sought, and other behavioral indicators.
By analyzing usage patterns, marketers can identify distinct segments within their target market and tailor marketing strategies to meet the unique needs and preferences of each segment. This enables companies to develop more targeted marketing campaigns, optimize product offerings, improve customer satisfaction, and drive customer loyalty.
Overall, behavioral segmentation, including the consideration of usage patterns, allows companies to better understand and connect with their customers by aligning their marketing efforts with specific behaviors and motivations.
To learn more about behavioral segmentation
https://brainly.com/question/30667392
#SPJ11
A study on the average minutes spent by students on internet usage is 300 with a standard deviation of 102. Answer the following questions assuming a bell-shaped distribution and using the empirical rule. What percentage of students use the internet for more than 402 minutes?.
Answers
The percentage of students that use the internet for more than 402 minutes = 16%
Percentage
Percentage, often referred to as percent, is a fraction of 100. Percentage means "per 100," and denotes part a total amount. For example, 45% represents 45 out of 100.
calculate the percentage-
The empirical rule states that
68% of the population lies within 1 standard deviation of the mean
95% of the population lies within 2 standard deviations of the mean
99.7% of the population lies within 3 standard deviations of the mean
Standard Deviation
A standard deviation (or σ) is a measure of how dispersed the data is in relation to the mean. Low standard deviation means data are clustered around the mean, and high standard deviation indicates data are more spread out.
The percentage will be illustrated in this:
P(X > 402) = P(X > 30 + 1 × 102)
= (1-0.68) / 2
= 0.32/2
= 16%
The percentage of students that use the internet for more than 402 minutes = 16%.
To learn more about Standard Deviation visit:
brainly.com/question/13905583
#SPJ4
Is the relation a function?
y = 2(x +1)^2- 8
Answers
Suppose a normal distribution has a mean of 150 and a standard deviation of 25. a. Approximately what percentage of the observations should we expect to lie between 125 and 225 ? Enter your answer to two decimal places. % of observations b. Approximately what percentage of the observations should we expect to lie between 75 and 200 ? Enter your answer to two decimal places. \% of observations c. Would a data value of 107 be considered as unusual for this particular normal distribution? No Yes d. Would a data value of 206 be considered as unusual for this particular normal distribution? No d. Would a data value of 206 be considered as unusual for this particular normal distribution? e. Suppose that the standard deviation is unknown. However, it is known that the smallest data value is 90 and the largest data value is 210. Assuming a small sample size, use the Ronge Rule of Thumb to estimate the unknown standard deviation Round your answer to one decimal place. Estimated standard deviation = f. Assuming a large sample size, use the Ronge Rule of Thumb to estimate the unknown standard deviation given that the smallest data value is 90 and the largest data value is 210 . Round your answer to one decimal ploce. Estimated standard deviation =
Answers
a. Approximately 95.45% of the observations are expected to lie between 125 and 225 in a normal distribution with a mean of 150 and a standard deviation of 25.
b. Approximately 81.85% of the observations are expected to lie between 75 and 200 in the same normal distribution.
a. To find the percentage of observations between 125 and 225, we calculate the z-scores for these values using the formula z = (x - μ) / σ, where x is the value, μ is the mean, and σ is the standard deviation. The z-score for 125 is (125 - 150) / 25 = -1, and the z-score for 225 is (225 - 150) / 25 = 3. We then look up the corresponding area under the normal distribution curve using a z-table or calculator. The area between -1 and 3 is approximately 0.9545, which corresponds to 95.45%.
b. Similarly, to find the percentage of observations between 75 and 200, we calculate the z-scores for these values. The z-score for 75 is (75 - 150) / 25 = -3, and the z-score for 200 is (200 - 150) / 25 = 2. We find the area between -3 and 2 under the standard normal distribution curve, which is approximately 0.8185 or 81.85%.
c. A data value of 107 would be considered unusual if it falls more than a few standard deviations away from the mean. To determine if it is unusual, we calculate the z-score for 107 using the formula (107 - 150) / 25 = -1.72. If we consider values outside the range of ±2 standard deviations as unusual, then 107 falls within this range and would not be considered unusual.
d. Similarly, for a data value of 206, the z-score is (206 - 150) / 25 = 2.24. Since it falls within the range of ±2 standard deviations, it would not be considered unusual.
e. The Range Rule of Thumb suggests that for a small sample size, the estimated standard deviation is approximately the range divided by 4. In this case, the range is 210 - 90 = 120, so the estimated standard deviation would be 120 / 4 = 30.
f. For a large sample size, the estimated standard deviation using the Range Rule of Thumb is approximately the range divided by 6. Therefore, the estimated standard deviation would be 120 / 6 = 20.
Learn more about normal distribution here:
https://brainly.com/question/15103234
#SPJ11
very fast
Show, by induction, that \( T(n)=10 n^{2}-3 n \quad \) if \( n=1 \)
Answers
Given that \(\(T(n)\) = \(10n^2-3n\)\) if (\(\(n=1\)\)), you have to prove it by induction. So, we have proved it by induction that \($$\(T(n)=10n^2-3n\)$$\) if ( n= 1). The given statement is true for all positive integers n
Let's do it below: The base case (n=1) is given as follows: \(T(1)\) =\(10\cdot 1^2-3\cdot 1\\&\)=\(7\end{aligned}$$\). This implies that \(\(T(1)\)\) holds true for the base case.
Now, let's assume that \(\(T(k)=10k^2-3k\)\) holds true for some arbitrary \(\(k\geq 1\).\)
Thus, for n=k+1, T(k+1) = \(10(k+1)^2-3(k+1)\\&\) = \(10(k^2+2k+1)-3k-3\\&\)=\(10k^2+20k+7k+7\\&\) = \(10k^2-3k+20k+7k+7\\&\) = \(T(k)+23k+7\\&\) = \((10k^2-3k)+23k+7\\&\) = \(10(k+1)^2-3(k+1)\).
Therefore, we have proved that the statement holds true for n=k+1 as well. Hence, we have proved it by induction that \($$\(T(n)=10n^2-3n\)$$\) if (n=1). Therefore, the given statement is true for all positive integers n.
For more questions on: integers
https://brainly.com/question/17695139
#SPJ8
Solve -6x +18> -30.
A. x < 2
B. x > 2
C. x > 8
D. x < 8
Answers
Answer: D, x < 8
Step-by-step explanation: Subtract 18 from both sides.
Simplify the expression
Subtract the numbers
Subtract the numbers
Divide both sides by the same factor, and flip the relation because the factor is negative
Cancel terms that are in both the numerator and denominator
Divide the numbers
−6x+18−18>−30−18=
=x<8
what is the answer to this? 4(w−6)≤−12
Answers
Step-by-step explanation:
\(4(w - 6) \leqslant - 12 \\ \)
\(4w - 24 \leqslant - 12\)
\(4w \leqslant - 12 + 24 \\ \)
\(4w \leqslant 12\)
What is the domain of G
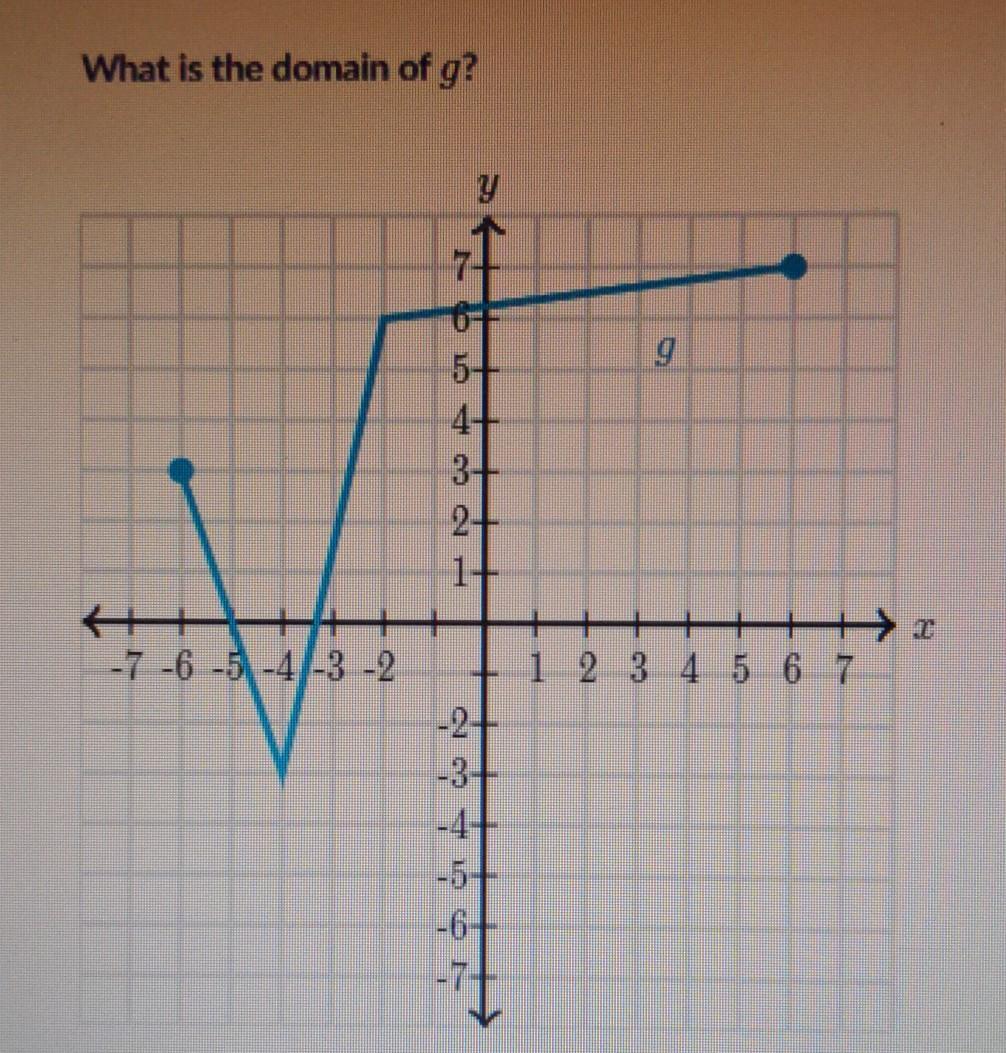
Answers
Answer:
D: {-6, 6}
Step-by-step explanation:
The domain are all the possible values for x. For this graph in the x-position, it starts from -6 to +6. Therefore, the domain will be {-6,6}.
Answer:
\(-6\leq x\leq 6\)
\(x\) ∈ \([-6, 6]\)
Step-by-step explanation:
The domain is the set of all numbers for which a function is defined. As one can see on the given graph, the function spans between the numbers (-6) and (6). Therefore, the function is defined between the numbers (-6) and (6). The closed dots on either end of the function signify that the function includes these values. Thus, the domain of the function is as follows:
(\(-6\leq x\leq 6\))
In set notation,
(\(x\) ∈ \([-6, 6]\))
–81, 108, –144, 192,. Which formula can be used to describe the sequence?.
Answers
The formula that can be used to describe the sequence is:\(a(n) = (-1)^(n+1) * 3^(n) * 4.\)
The given sequence is -81, 108, -144, 192.
The formula that can be used to describe the sequence is: \(a(n) = (-1)^(n+1) * 3^(n) * 4\), where n is the nth term in the sequence.
This formula is a geometric sequence formula that can be used to describe the given sequence.
The formula represents the nth term of the sequence as a function of the position of the term in the sequence.
Here, n represents the position of the term in the sequence
.For the given sequence, the first term is -81, which corresponds to the first position in the sequence (n = 1).
The second term is 108, which corresponds to the second position in the sequence (n = 2).
The third term is -144, which corresponds to the third position in the sequence (n = 3).
The fourth term is 192, which corresponds to the fourth position in the sequence (n = 4).
Therefore, the formula that can be used to describe the sequence is: \(a(n) = (-1)^(n+1) * 3^(n) * 4.\)
Know more about sequence here:
https://brainly.com/question/7882626
#SPJ11
Which statement about the function is true?
O The function is increasing for all real values of x
where
x<-4.

Answers
Answer:
A.) The function is increasing for all real values of x where x < -4
Step-by-step explanation:
On the interval x < -4, all of the x values are increasing. Before x = -4, the line assumes a positive slope because it is heading upwards. After this interval, the function is decreasing because the slope is heading downwards.
On the interval -6 < x < -2, all of the x values are positive because they lie above the x-axis. This does not necessarily mean that all of the values are increasing.
On the interval x < -6 and x > -2, all of the x values are negative because they lie below the x-axis.
Determine whether the sequence converges or diverges. If it converges, find the limit. A) a n = √ 1 + 4 n 2 1 + n 2 B) a n = cos 2 n 2 n
Answers
The answers are:
A) The sequence converges to 1.
B) The sequence diverges.
For sequence A, we can simplify the expression by dividing both the numerator and denominator by n^2. This gives us:
a_n = √(1 + 4/n^2)/(1 + 1/n^2)
As n approaches infinity, the terms in the denominator become negligible compared to the terms in the numerator. Therefore, the sequence converges to:
lim a_n = √(1 + 0)/1 = 1
For sequence B, we know that the cosine function oscillates between -1 and 1, so the sequence will oscillate as well. As n approaches infinity, the terms in the denominator become larger, causing the oscillations to become more rapid. However, the sequence will never approach a single value, so it diverges.
Know more about converges here:
https://brainly.com/question/15415793
#SPJ11
based on the design of the study, would a statistically significant result allow the researchers to conclude that receiving treatments at the clinic you selected in part (a-ii) causes a higher percentage of successful treatments than at the other clinic? explain your answer.
Answers
No, a statistically significant result would not allow the researchers to conclude that receiving treatments at the clinic selected in part (a-ii) causes a higher percentage of successful treatments than at the other clinic.
The study design is a comparison of the success rates of the two clinics without controlling for any other variables that may influence the results. In order to conclude that the clinic you selected causes higher success rates, the researchers would need to control for other variables, such as the types of treatments, the types of patients, the experience of the clinicians, etc.
Learn more about Statistics here:
https://brainly.com/question/15525560
#SPJ4
A cylinder has a volume of 45 pi and radius of 3 what is the height? Plzz help it’s due tomorrow
Answers
Answer:
Height = 5
Step-by-step explanation:
\(Solution,\\Volume(V)=45\pi \\Radius(r)=3\\Height(h)=?\\As,\\V=\pi r^{2} h\\45\pi =\pi (3)^{2} h\\\frac{45\pi }{9\pi } =h\\h=5\)
evaluate j'y y dx both directly and using green's theorem, where ' is the semicircle in the upper half-plane from r to - r.
Answers
Using Green's Theorem: ∫_' \(y^2\) dx =\(r^4\)/6
Let's first find the parametrization of the semicircle ' in the upper half-plane from r to -r.
We can use the parameterization r(t) = r(cos(t), sin(t)) for a circle centered at the origin with radius r, where t varies from 0 to pi.
To restrict to the upper half-plane, we can choose t to vary from 0 to pi/2. Thus, a possible parametrization for ' is given by:
r(t) = r(cos(t), sin(t)), where t ∈ [0, pi/2]
Now, we can evaluate the line integral directly:
∫_' \(y^2\) dx = ∫_0^(pi/2) (r sin\((t))^2\) (-r sin(t)) dt
= -\(r^4\) ∫_\(0^\)(\(\pi\)/2) \(sin^3\)(t) dt
= -\(r^4\) (2/3)
To use Green's Theorem, we need to find a vector field F = (P, Q) such that F · dr = y^2 dx on '.
One possible choice is F(x, y) = (-\(y^3\)/3, xy), for which we have:
∫_' F · dr = ∫_\(0^(\pi\)/2) F(r(t)) · r'(t) dt
= ∫_\(0^(\pi\)/2) (-\(r(t)^3\)/3, r(t)^2 sin(t) cos(t)) · (-r sin(t), r cos(t)) dt
= ∫_\(0^(\pi/2) r^4\)/3 \(sin^4\)(t) + \(r^4\)/3 \(cos^2\)(t) \(sin^2\)(t) dt
= \(r^4\)/3 ∫_\(0^(pi/2)\)\(sin^2\)(t) (\(sin^2\)(t) + \(cos^2\)(t)) dt
= \(r^4\)/3 ∫_\(0^(\pi/2\)) \(sin^2\)(t) dt
= \(r^4\)/6
Thus, we have:
∫_' \(y^2\) dx = ∫_' F · dr = \(r^4\)/6
Therefore, the two methods give us the following results:
Direct evaluation: ∫_'\(y^2\)dx = -\(r^4\) (2/3)
Using Green's Theorem: ∫_' \(y^2\) dx = \(r^4\)/6
For more such answers on parameterization
https://brainly.com/question/29673432
#SPJ11
We get the same result as before, J'y y dx = 0, using Green's Theorem.
To evaluate J'y y dx directly, we need to parameterize the curve ' and substitute the appropriate variables.
Let's parameterize the curve ' by using polar coordinates. The curve ' is a semicircle in the upper half-plane from r to -r, so we can use the parameterization:
x = r cos(t), y = r sin(t), where t ranges from 0 to π.
Then, we have y = r sin(t) and dy = r cos(t) dt. Substituting these variables into the expression for J'y y dx, we get:
J'y y dx = ∫' y^2 dx = ∫t=0^π (r sin(t))^2 (r cos(t)) dt
= r^3 ∫t=0^π sin^2(t) cos(t) dt.
To evaluate this integral, we can use the identity sin^2(t) = (1 - cos(2t))/2, which gives:
J'y y dx = r^3 ∫t=0^π (1/2 - cos(2t)/2) cos(t) dt
= (r^3/2) ∫t=0^π cos(t) dt - (r^3/2) ∫t=0^π cos(2t) cos(t) dt.
Evaluating these integrals gives:
J'y y dx = (r^3/2) sin(π) - (r^3/4) sin(2π)
= 0.
Now, let's use Green's Theorem to evaluate J'y y dx. Green's Theorem states that for a simple closed curve C in the plane and a vector field F = (P, Q), we have:
∫C P dx + Q dy = ∬R (Qx - Py) dA,
where R is the region enclosed by C, and dx and dy are the differentials of x and y, respectively.
To apply Green's Theorem, we need to choose an appropriate vector field F. Since we are integrating y times dx, it's natural to choose F = (0, xy). Then, we have:
Py = x, Qx = 0, and Qy - Px = -x.
Substituting these values into the formula for Green's Theorem, we get:
∫' y dx = ∬R (-x) dA.
To evaluate this double integral, we can use polar coordinates again. Since the curve ' is a semicircle in the upper half-plane, the region R enclosed by ' is the upper half-disc of radius r. Using polar coordinates, we have:
x = r cos(t), y = r sin(t), where r ranges from 0 to r and t ranges from 0 to π.
Then, we have:
∬R (-x) dA = ∫r=0^r ∫t=0^π (-r cos(t)) r dt dθ
= -r^2 ∫t=0^π cos(t) dt ∫θ=0^2π dθ
= 0.
Know more about Green's Theorem here:
https://brainly.com/question/30763441
#SPJ11
3/5 = 4m.
What does m equal?
Answers
First, flip the equation around.
3/5=4m
4m=3/5
Now simplify by dividing 4 from both sides.
4m=3/5
/4 /4
m=0.15 or 3/20
---
hope it helps
The value of m will be equal to 3 / 20.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the expression is 3 / 5 = 4m. The value of m will be calculated as:-
First, flip the equation around.
3/5=4m
4m=3/5
Now simplify by dividing 4 from both sides.
4m = 3/5
m = 0.15
m = 3/20
To know more about an expression follow
https://brainly.com/question/15300073
#SPJ2
What doee this mean in Zybook?
Complete this statement to increment y:
y = _____
Answers
y = y + 1
among drivers insured by an insurance company 64% are women, 35% of the drivers are in a high risk catergory, and 20% of the drivers are high risk women. if a driver is randomnly selected from that company, what is the probability that the driver is either high risk or a woman
Answers
Answer:
2/3
Step-by-step explanation:
If u had powers what power would u have

Answers
Answer:
I would have psychic powers so I could have multiple powers.
Fraction: 1/11, Numerator: 1
Step-by-step explanation:
Brandon has 32 stamps he wants to display the stamps in a row with the same number of stamps in each row how many ways can he display the stamps explain
Answers
Answer:
6 ways
Step-by-step explanation:
The number of ways he can display the stamps as follows:
Here we find the factors of 32
i.e.
= 1 × 32 represent 1 row, 32 stamps each
= 2 × 16 represent 2 rows, 16 stamps each.
= 4 × 8 represent 4 rows, 8 stamps each.
= 8 × 4 represent 8 rows with 4 stamps each
= 16 × 2 represent 16 rows with 2 stamps each
= 32 × 1 represent 32 rows with 1 stamp each
So in 6 ways he can displayed
a. What is the probability that an individual bottle contains less than 2.11 liters?
(Round to three decimal places as needed.)
b. If a sample of 4 bottles is selected, what is the probability that the sample mean amount contained is less than 2.11 liters?
(Round to three decimal places as needed.)
c. If a sample of 25 bottles is selected, what is the probability that the sample mean amount contained is less than 2.11 liters?
(Round to three decimal places as needed.)
d. Explain the difference in the results of (a) and (c).
Part (a) refers to an individual bottle, which can be thought of as a sample with sample size Therefore, the standard error of the mean for an individual bottle is standard error of the sample in (c) with sample size 25. This leads to a probability in part (a) that is the probability in part (c). times the
(Type integers or decimals. Do not round.)
Answers
To solve this problem, we will use the normal distribution. We are given that the mean amount in a bottle is 2.11 liters, and the standard deviation is not provided.
a. To find the probability that an individual bottle contains less than 2.11 liters, we need to calculate the area under the normal curve to the left of 2.11 liters. Since the standard deviation is not given, we cannot calculate the z-score directly. However, assuming a normal distribution, we can use the z-table or a statistical software to find the corresponding z-value and its associated probability. Let's assume the z-value is -1.96, the probability can be calculated as P(Z < -1.96) ≈ 0.025. Therefore, the probability that an individual bottle contains less than 2.11 liters is approximately 0.025.
b. When a sample of 4 bottles is selected, probability that sample mean amount is less than 2.11 liters can be calculated using Central Limit Theorem. Since the sample size is small (n < 30), we can assume the sampling distribution of the sample mean follows a t-distribution. However, since the standard deviation is not provided, we cannot calculate the exact probability. We need more information to proceed. c. Similar to part (b), when a sample of 25 bottles is selected, the probability that the sample mean amount is less than 2.11 liters can be calculated using the Central Limit Theorem. With a larger sample size, we can assume the sampling distribution of the sample mean follows a normal distribution. Again, since the standard deviation is not provided, we cannot calculate the exact probability. We need more information to proceed.
d. The difference in the results of parts (a) and (c) is due to the sample size. In part (a), we are considering the probability for an individual bottle, which can be seen as a sample with a sample size of 1. In part (c), we are considering the probability for a sample of 25 bottles. As the sample size increases, the distribution of the sample mean becomes closer to a normal distribution, allowing us to make more precise probability calculations. The Central Limit Theorem states that as the sample size increases, the distribution of the sample mean approaches a normal distribution regardless of the shape of the population distribution. Therefore, we can make more accurate probability estimates when we have a larger sample size.
To learn more about normal distribution click here : brainly.com/question/15103234
#SPJ11
how many terms are in the following expression?
Answers
The number of terms in the expression, 6 + 2 x - 4 y + 5 z is 4 terms.
How to find the number of terms ?In the expression 6 + 2x - 4y + 5z, the number of terms is four, not the number of signs. The terms in this expression are:
62 x- 4 y 5 zEach term is separated by an operator (either addition or subtraction), which is represented by a sign. Therefore, the expression contains three addition signs and one subtraction sign.
Find out more on the number of terms at https://brainly.com/question/30659621
#SPJ1
The full question is:
How many terms are in the following expression 6 + 2 x - 4 y + 5 z
help please! i'll be sure to mark brainliest if i'm able to!

Answers
Answer: its the first 3 i think
Step-by-step explanation:
Answer:they are not congruent
Step-by-step explanation:
After a shopping trip, the amount of money
Katrina has left can be modeled by the expression
75-9. 5t-11. 75s, where t is the number of t-shirts
and s is the number of pairs of shorts Katrina bought.
a. Describe what each term of the expression
represents in this situation.
b. How many t-shirts and shorts might Katrina have
bought?
Answers
Answer:
66
Step-by-step explanation:
ANSWER FAST PLEASE
10.
The first four numbers in a quadratic sequence are
shown below.
2, 3, 6, 11,...
What is the next number in the sequence?
A.
16
B.
18
C. 22
D. 27

Answers
Answer:
B.18
Step-by-step explanation:
2+1+3
3+3=6
6+5=11
11+7=18
6 - 3 = 3
3 - 2 = 1
Notice how all the differences is an odd number. The number after 11 needs have a difference of 7 when subtracted so it would be B. This sequence is an arithmetic sequence.
Answer: 18
Hope you learned something new! :D
What type of function is this Linear or Exponential?

Answers
The function y = 3x + 7 is a linear function and the second function that is represented in table is an exponential function.
What is a linear and exponential function?The way the y-values change when the x-values increase by a constant amount differs between linear and exponential relationships: The y-values in a linear relationship differ by the same amount. The y-values in an exponential relationship have equal ratios.Linear functions have a straight line as their graph. There is one independent variable and one dependent variable in a linear function. x and y are independent and dependent variables. An exponential function is a mathematical function with the formula f (x) = aˣ, where "x" is a variable and "a" is a constant that is called the function's base and must be greater than zero. The transcendental number e is the most commonly used exponential function base.Here the function y = 3x + 7 is a linear function and the second function is an exponential function because powers of 2.
To learn more about functions refer to :
https://brainly.com/question/725335
#SPJ1