A sequence , satisfies the recurrence relation with
initial
conditions and . Find an explicit formula for the sequence.
+ k2 3) A sequence a,,a,,a z ..., satisfies the recurrence relation ax = 2x-1 + 2ax-2 with initial conditions a, = 2 and a = 7. Find an explicit formula for the sequence.
Answers
The explicit formula for the sequence \(\(a_n\)\) is:
\(\(a_n = \begin{cases} 4n + 3 & \text{if } n \text{ is even} \\ 4n - 2 & \text{if } n \text{ is odd} \end{cases}\)\)
To find an explicit formula for the sequence \(\(a_n\)\) that satisfies the recurrence relation \(\(a_n = 2n-1 + 2a_{n-2}\)\) with initial conditions \(\(a_1 = 2\)\) and \(\(a_2 = 7\)\), we can proceed as follows:
First, let's examine the first few terms of the sequence:
\(\(a_1 = 2\)\\\(a_2 = 7\)\\\(a_3 = 2(3) - 1 + 2a_1 = 5 + 2(2) = 9\)\\\(a_4 = 2(4) - 1 + 2a_2 = 8 + 2(7) = 22\)\\\(a_5 = 2(5) - 1 + 2a_3 = 9 + 2(9) = 27\)\\\)
We can observe that the even-indexed terms \(\(a_2, a_4, a_6, \ldots\)\) are increasing by a factor of 2, while the odd-indexed terms \(\(a_1, a_3, a_5, \ldots\)\) are increasing by a factor of 3. This pattern suggests that we can split the sequence into two separate sequences:
For even-indexed terms:
\(\(b_n = a_{2n}\)\)
For odd-indexed terms:
\(\(c_n = a_{2n-1}\)\)
Let's find explicit formulas for both \((\(b_n\))\) and \((\(c_n\))\):
1. Even-indexed terms \((\(b_n\))\):
The recurrence relation becomes:
\(\(b_n = 2(2n) - 1 + 2b_{n-1}\)\)
To simplify the formula, let's rewrite \(\(b_n\)\) as \(\(b_{n+1}\)\) (i.e., shifting the index by 1):
\(\(b_{n+1} = 2(2n + 2) - 1 + 2b_{n}\)\)
Subtracting the two equations, we get:
\(\(b_{n+1} - b_n = 4\)\)
This is a simple arithmetic progression with a common difference of 4. To find an explicit formula for \(\(b_n\)\), we can use the formula for the nth term of an arithmetic progression:
\(\(b_n = b_1 + (n - 1) \cdot \text{{common difference}}\)\)
Substituting \(\(b_1 = a_2 = 7\)\) and the common difference of 4, we have:
\(\(b_n = 7 + (n - 1) \cdot 4 = 4n + 3\)\)
2. Odd-indexed terms \((\(c_n\))\):
The recurrence relation becomes:
\(\(c_n = 2(2n-1) - 1 + 2c_{n-1}\)\)
Similar to before, let's rewrite \(\(c_n\)\) as \(\(c_{n+1}\)\):
\(\(c_{n+1} = 2(2n + 1) - 1 + 2c_{n}\)\)
Subtracting the two equations, we get:
\(\(c_{n+1} - c_n = 4\)\)
Again, this is an arithmetic progression with a common difference of 4. Applying the formula for the nth term of an arithmetic progression:
\(\(c_n = c_1 + (n - 1) \cdot \text{{common difference}}\)\)
Substituting \(\(c_1 = a_1 = 2\)\) and the common difference of 4, we have:
\(\(c_n = 2 + (n - 1) \cdot 4 = 4n-2\)
1) \(\cdot 4 = 4n - 2\)\)
Now that we have explicit formulas for both \(\(b_n\)\) and \(\(c_n\)\), we can combine them to obtain the explicit formula for the original sequence \(\(a_n\)\):
For even-indexed terms, \(\(a_{2n} = b_n = 4n + 3\)\)
For odd-indexed terms, \(\(a_{2n-1} = c_n = 4n - 2\)\)
Therefore, the explicit formula for the sequence \(\(a_n\)\) is:
\(\(a_n = \begin{cases} 4n + 3 & \text{if } n \text{ is even} \\ 4n - 2 & \text{if } n \text{ is odd} \end{cases}\)\)
Learn more about Arithmetic Progression at:
https://brainly.com/question/30442577
#SPJ4
Related Questions
I need help with this pls

Answers
Answer:
JanetStep-by-step explanation:
Because janet daily step count is 5000-9000And brends step count is7000-10000Janat step count is 1000 greater than brenda.Please mark me brainalist.Which inequality has a solid boundary line when graphed?
y<-x-9
y< 1/9x+9
y>-1/9x
y>=9x+9
Answers
The inequality that has a solid boundary line when graphed is y ≥ 9x + 9 (option d).
1. The inequality y < -x - 9 has a dashed boundary line when graphed. The symbol "<" indicates that the line is not included in the solution set, hence the dashed line.
2. The inequality y < (1/9)x + 9 also has a dashed boundary line when graphed. Similar to the previous inequality, the "<" symbol implies that the line is not part of the solution set, resulting in a dashed line.
3. The inequality y > -(1/9)x does not have a solid boundary line when graphed. The ">" symbol signifies that the line is not included in the solution set, resulting in a dashed line.
4. The inequality y ≥ 9x + 9 has a solid boundary line when graphed. The "≥" symbol indicates that the line is part of the solution set, leading to a solid line.
Graphically, the solid boundary line in the fourth inequality represents all the points on the line itself, including the line. The inequality y ≥ 9x + 9 includes all the points above and on the line.
For more such questions on inequality, click on:
https://brainly.com/question/30238989
#SPJ8
you place in a dark bag 24 marbles. 12 marbles are red, 5 marbles are blue and 7 marbles are yellow. you select 2 random marbles (one after the other without putting the first back in). what is the probability that the marbles have the same color?
Answers
The probability of selecting two marbles with the same color is approximately 0.27 or 27%.
To work out the likelihood that the two marbles drawn have similar variety, we can utilize the accompanying advances:
In the first place, we compute the likelihood of drawing a red marble on the principal pick: 12/24 = 1/2.
On the off chance that the main marble drawn is red, there will be 11 red marbles left clinched, out of a sum of 23 marbles. So the likelihood of drawing one more red marble on the subsequent pick is 11/23.
Likewise, in the event that the principal marble drawn is blue, there will be 4 blue marbles left clinched, out of a sum of 23 marbles. So the likelihood of drawing one more blue marble on the subsequent pick is 4/23.
Furthermore, on the off chance that the main marble drawn is yellow, there will be 6 yellow marbles left taken care of, out of a sum of 23 marbles. So the likelihood of drawing one more yellow marble on the subsequent pick is 6/23.
To get the complete likelihood of drawing two marbles of similar variety, we want to add the probabilities of every one of these cases:
(1/2) x (11/23) + (5/24) x (4/23) + (7/24) x (6/23) = 55/138 or roughly 0.398 or 39.8%.
In this way, the likelihood of drawing two marbles of a similar variety is roughly 39.8%.
To learn more about numerical on probability, refer:
https://brainly.com/question/30736519
#SPJ4
Xavier needed to get his computer fixed. He took it to the repair store. The technician at the store worked on the computer for 4. 5 hours and charged him $155 for parts. The total was $357. 50. Write and solve an equation which can be used to determine xx, the cost of the labor per hour. ?
Answers
Answer:
The cost is $45 per hour.
Step-by-step explanation:
(h = hours)
1. The equation is 4.5h + 155 = 357.5.
2. Subtract 155 from both sides of the equal sign. The equation is 4.5h = 202.5.
3. Divide both sides by 4.5. The answer is h = 45.
A simple random sample of 500 elements generates a sample proportion p= 0.81. Provide the 90% confidence interval for the population proportion (to 4 decimals). b.Provide 95% the confidence interval for the population proportion (to 4 decimals).
Answers
a) The 90% confidence interval for the population proportion is approximately (0.7777, 0.8423).
b) The 95% confidence interval for the population proportion is approximately (0.7737, 0.8463).
To calculate the confidence intervals for the population proportion, we can use the formula:
Confidence Interval = sample proportion ± margin of error
The margin of error can be calculated using the formula:
Margin of Error = critical value * standard error
where the critical value is determined based on the desired confidence level and the standard error is calculated as:
Standard Error = \(\sqrt{((p * (1 - p)) / n)}\)
Given that the sample proportion (p) is 0.81 and the sample size (n) is 500, we can calculate the confidence intervals.
a. 90% Confidence Interval:
To find the critical value for a 90% confidence interval, we need to determine the z-score associated with the desired confidence level. The z-score can be found using a standard normal distribution table or calculator. For a 90% confidence level, the critical value is approximately 1.645.
Margin of Error = \(1.645 * \sqrt{(0.81 * (1 - 0.81)) / 500)}\)
≈ 0.0323
Confidence Interval = 0.81 ± 0.0323
≈ (0.7777, 0.8423)
Therefore, the 90% confidence interval for the population proportion is approximately (0.7777, 0.8423).
b. 95% Confidence Interval:
For a 95% confidence level, the critical value is approximately 1.96.
Margin of Error = \(1.96 * \sqrt{(0.81 * (1 - 0.81)) / 500)}\)
≈ 0.0363
Confidence Interval = 0.81 ± 0.0363
≈ (0.7737, 0.8463)
Thus, the 95% confidence interval for the population proportion is approximately (0.7737, 0.8463).
Learn more about confidence interval here:
brainly.com/question/32546207
#SPJ4
the unit value of a cubic centimeter is the same as which metric measurement?
Answers
Answer: The unit value of a cubic centimeter (cm^3) is the same as the metric measurement of a milliliter (mL).
This is because 1 milliliter is equal to 1 cubic centimeter. In other words, if you have a cube that measures 1 centimeter on each side, its volume would be 1 cubic centimeter, which would also be equivalent to 1 milliliter of volume.
This relationship between cm^3 and mL is commonly used in scientific and medical measurements involving liquids and gases.
The unit value of a cubic centimeter (cc) is equivalent to one milliliter (mL) in the metric system. Both cubic centimeters and milliliters are used to measure volume, and their conversion is straightforward: 1 cc = 1 mL.
The metric system uses base units such as meters, liters, and grams, and applies prefixes like kilo-, centi-, and milli- to indicate larger or smaller units of measurement.
Cubic centimeters are often used to measure the volume of solid objects or the capacity of containers, while milliliters are more commonly used to measure the volume of liquids. However, both units represent the same volume and can be used interchangeably.
It is important to understand the difference between volume measurements and other metric measurements, such as length or mass. For instance, meters are used to measure length or distance, and grams are used to measure mass or weight. These units cannot be directly converted to cubic centimeters or milliliters, as they represent different physical properties.
In summary, a cubic centimeter (cc) is a unit of volume in the metric system that is equivalent to one milliliter (mL). Both units can be used to measure volume, and they have a simple conversion of 1 cc = 1 mL. Understanding the relationship between these units and other metric measurements is essential for accurately quantifying and comparing different physical properties.
To learn more about a cubic centimeter, refer:-
https://brainly.com/question/16670888
#SPJ11
(a) cause-in-fact (b) assumption of risk (c) seclusion (d) res ipsa loquitur (e) slander (f) punitive damages (g) absolute privilege
Answers
The legal context and definitions are (a) Negligence - Establishes the link between the defendant's actions and the plaintiff's harm. (b) Negligence defenses - Plaintiff voluntarily accepts known risks, relieving the defendant of liability. (c) Invasion of privacy - Unjustified intrusion into private affairs that would offend a reasonable person. (d) Negligence - Accident itself suggests defendant's negligence without direct evidence (e) Defamation - False spoken statements harming someone's reputation (f) Monetary awards to punish and deter egregious behavior. (g) Defamation defenses - Immunity for certain statements made in specific contexts.
(a) Cause-in-fact
Legal context: Negligence.
Definition: Cause-in-fact refers to the actual cause or link between the defendant's conduct and the plaintiff's harm, establishing that the harm would not have occurred without the defendant's actions.
(b) Assumption of risk
Legal context: Negligence defenses.
Definition: Assumption of risk is a defense in negligence cases where the plaintiff voluntarily and knowingly accepts the risks associated with a certain activity, relieving the defendant of liability for any resulting harm.
(c) Seclusion
Legal context: Invasion of privacy.
Definition: Seclusion refers to the intentional and unjustified intrusion into an individual's private affairs or seclusion, which would highly offend a reasonable person.
(d) Res ipsa loquitur
Legal context: Negligence.
Definition: Res ipsa loquitur is a doctrine where the occurrence of an accident or injury itself suggests that the defendant was negligent, allowing the plaintiff to establish a prima facie case without direct evidence of negligence.
(e) Slander
Legal context: Defamation.
Definition: Slander is a form of defamation that involves making false spoken statements about someone that harm their reputation.
(f) Punitive damages
Legal context: Various tort subject areas.
Definition: Punitive damages are monetary awards beyond compensatory damages, awarded in certain cases to punish the defendant for particularly egregious behavior and to deter others from similar conduct.
(g) Absolute privilege
Legal context: Defamation defenses.
Definition: Absolute privilege is a defense in defamation cases that grants immunity from liability for statements made in certain contexts, such as during legislative or judicial proceedings, regardless of their truth or intent.
To know more about legal context:
https://brainly.com/question/28437027
#SPJ4
--The given question is incomplete, the complete question is given below " For each term (1) identify the legal context in which it arises; and (2) define the term.
For the legal context part of your answer for each term, indicate which tort subject area the term relates to (e.g., "fraud," “false imprisonment,” “defamation,” “defamation defenses,” “invasion of privacy,” “interference with contract,” “interference with prospective economic advantage,” “negligence,” “negligence defenses,” “strict liability,” or, if and where appropriate, “intentional torts” generally).
In addition, the definition portions of your answers need not be more than one sentence for each term. Your answer for each term is worth a maximum of 2 points.
(a) cause-in-fact
(b) assumption of risk
(c) seclusion
(d) res ipsa loquitur
(e) slander
(f) punitive damages
(g) absolute privilege"--
Marsha is filing her federal income tax return with the Single filing status. She had an adjusted gross income of $56,800 last year and is trying to decide whether to take the standard deduction of $5700 or to itemize deductions. Last year she had $4900 in medical expenses, $3100 in state and local income taxes paid, $1940 in mortgage interest paid, $530 in charitable contributions, and $1200 in non-reimbursed work expenses
Answers
Marsha must claim for itemized deductions.
Given,
Last year's gross income is $56,800.
Medical expenses = $4900
State and local income taxes paid = $3100
The mortgage interest paid = $1940
Charitable contributions = $530
Non-reimbursed work expenses = $1200
Standard deduction = $5700
The sum of all the expenses of last year = $4900 + $3100 + $1940 + $530 + $1200 = $11,670
And the Standard deduction is $5700.
Which is, $11,670 - $5700 = $5970 lesser.
Therefore, Marsha must claim for itemize deductions rather than the standard deductions.
Learn more about itemized deductions and standard deductions at
https://brainly.com/question/12530643?referrer=searchResults
#SPJ4
please help, it’s urgent

Answers
Answer:
x= 102 degrees
Step-by-step explanation:
It is an isosceles triangle, which means that it has two equal sides and angles, so the angles opposite of 3.3 are going to be the same or 39 degrees, which means, 39 + 39 is 78 and 180 - 78 is 102 and x=102 degrees.
Rob has -180 points in a game. He gains one-fourth of his points back on his next turn, and
gains back an additional one-fifth of his remaining points on his second turn.
What is Rob's score at the end of the two turns?
A
-72 points
B
-108 points
С
-135 points
D
-171 points
Answers
Answer:
171 is the answer of that question
for the following conjecture, state the null and alternative hypotheses. the average weight loss for a sample of people who exercise 30 minutes per day for 6 weeks is greater than 8.2 pounds.
Answers
For the given conjecture, which is "the average weight loss for a sample of people who exercise 30 minutes per day for 6 weeks is greater than 8.2 pounds", the null and alternative hypotheses can be stated as follows:
Null Hypothesis (H0): The average weight loss for the sample is equal to or less than 8.2 pounds (≤ 8.2 lbs).
Alternative Hypothesis (H1): The average weight loss for the sample is greater than 8.2 pounds (> 8.2 lbs).
These hypotheses are formed to test whether there is significant evidence to support the conjecture that exercising 30 minutes per day for 6 weeks leads to an average weight loss of more than 8.2 pounds.
Learn more about hypotheses here:
https://brainly.com/question/18064632
#SPJ11
What is the interest of an investment of $2,000 made at 6% simple interest per year for a time period of 9 mo.?
Answers
Answer:The answer would be $1080.
I need help with this please help .

Answers
Answer:
Subs: 49.5 students, Tex-mex: 144 students, Italian: 31.5 students
Step-by-step explanation
The number of students eating a type of food can be found by using:
Percent * number of students
So in this equation, we can use this formula to find the answers.
Subs:
22% * 225 = 0.22 * 225 = 49.5
Tex-mex:
64% * 225 = 0.64 * 225 = 144
Italian:
14% * 225 = 0.14 * 225 = 31.5
There is an issue- you can't have half a person. Either this question is wrong, or the person who wrote it didn't keep this in mind.
Ask your teacher whether this question is right, or just leave the answer like this.
Use your knowledge to set up equations and solve for the variables.

Answers
Answer:
x = 45 degrees
Step-by-step explanation:
Using the alternate exterior angle theorem, the angles are equal. You can set the expressions equal to each other:
3x = x + 90
2x = 90
x = 45
The segments shown below could form a triangle.
A
с
B
4
9
B
15
A
A. True
B. False

Answers
Answer: True.
Step-by-step explanation:
do the math and u will see
No, The segments shown below could not form a triangle.
What is mean by Triangle?A triangle is a three sided polygon, which has three vertices and three angles which has the sum 180 degrees.
Given that;
Three line segment with measure 9 , 4 and 15 are shown.
We know that;
The sum of two sides of a triangle are always greater than the third side,
Here, 9 + 4 = 13 < 15
Hence, The segments shown below could not form a triangle.
Thus, The segments shown below could not form a triangle.
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ7
The amalie arena in tampa contains the largest high-definition center-hung display in the country. the rectangular display has an area of about 1400 square feet and its width is 6 feet less than twice its height. find the width and height of the display.
Answers
The width and height of the rectangular display is 50 feet and 28 feet, respectively.
Using algebraic expression and equation, we can find the dimensions of the rectangular display.
Let x be the height of the display
If its width is 6 feet less than twice its height, then the width can be represented as the algebraic expression:
2x - 6 = width of the display
If the area of the display is 1400 square feet, then the equation to represent this relationship:
A = height x width
1400 = x(2x - 6)
Expanding the expression on the right-hand side:
1400 = 2x² - 6x
Dividing the whole equation by 2,
x² - 3x - 700 = 0
Factor the equation,
(x - 28)(x + 25) = 0
x = 28 ; -25
Taking the positive dimension,
height = 28 feet
So the height of the display is 28 feet. To find the width, we can use the expression we derived earlier:
width = 2x - 6
width = 2(28) - 6
width = 50 feet
So the width of the display is 50 feet.
Learn more about algebraic expression and equation here: https://brainly.com/question/4344214
#SPJ4
4,3,9/4,27/16
what is the 10th term of the sequence
Answers
Answer:
This is a sequence, so we have to move forward step by step
Step-by-step explanation:
4,3,9/4,27/16
Because this sequence has no exponential arithmetic or geometry, we perform the sequence with the help of a matrix
\(y = y\)
\(x = x\)
\(x = 4.4.4.4.4\)
\(x = 4\)
Matrix determinants allowed us to achieve both geometric and arithmetic progression by sequence guidance
The answer is
\(x \times y = 144 = 614.88\)
= 7.1 Zero and Negative Exponents
Which choice is correct?
Write an equivalent expression
with positive exponents only.
Help ??☠️☠️

Answers
Answer:
D
Step-by-step explanation:
\(x^{7}\)y^-3
keep x^7 on top and bring y^-3 to the bottom to make the exponent positive
\(x^{7}\)/\(y^{3}\)
The next pages are the same problem they are all D
solve
a- 7-2 = 4x-5
b- Simplify
3x(x+6)-3x(6-3x)
Answers
Answer:
x=5/4 + 5b/4
b= -1+ 4x/5
The other one is 12x^2
Step-by-step explanation:
i asked my online computer tutoring app thingy
Answer:
1) x=-0.5 and x=-3.41
2) 12x^2
Step-by-step explanation:
a) 7-x^2=4x-5
7-x^2-4x+5=0
-x^2-4x-2=0
Multiply by -1
x^2+4x+2=0
Solve using quadratic formula \($x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$\)
we have a=1, b=4, c=2
Putting values to find x
\(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\x=\frac{-(4)\pm\sqrt{(4)^2-4(1)(2)}}{2(1)}\\x=\frac{-4\pm\sqrt{16-8}}{2}\\x=\frac{-4\pm\sqrt{8}}{2}\\x=\frac{-4+\sqrt{8}}{2} \ and \ x=\frac{-4-\sqrt{8}}{2}\\x=-0.5 \ and \ x=-3.41\)
So, x=-0.5 and x=-3.41
b) Simplify
\(3x(x+6)-3x(6-3x)\)
\(3x(x+6)-3x(6-3x)\\=3x^2+18x-18x+9x^2\\=3x^2+9x^2\\=12x^2\)
Find the slope of Y=4x-5 in line parallel
Answers
Answer
slope of 4x - 5: m = 4
Find a 99% confidence interval for the average number of hours a student spends studying for a statistics exam if o is known to be 6.25 hours and a sample of 50 students has x=4 (3.176.4.824)(1.941, 6.059)(3.307, 4.693) (3.090,4.910(3.650.4.350) (1.724,6 276)
Answers
The 99% confidence interval for the average number of hours a student spends studying for a statistics exam is (2.059, 5.941) hours.
To find a 99% confidence interval for the average number of hours a student spends studying for a statistics exam, we can use the formula:
CI = x ± z*(o/sqrt(n))
where CI is the confidence interval, x is the sample mean, z is the z-score for the desired confidence level (in this case, 99%), o is the population standard deviation, and n is the sample size.
Plugging in the given values, we get: CI = 4 ± 2.576*(6.25/sqrt(50)) CI = 4 ± 1.941 CI = (2.059, 5.941)
Therefore, the 99% confidence interval for the average number of hours a student spends studying for a statistics exam is (2.059, 5.941) hours.
Learn more about confidence interval,
https://brainly.in/question/39892400
#SPJ11
true or false: if you are given a graph with two shiftable lines, the correct answer will always require you to move both lines.
Answers
False. if you are given a graph with two shif table lines, the correct answer will always require you to move both lines.
In a graph with two shiftable lines, the correct answer may or may not require moving both lines. It depends on the specific scenario and the desired outcome or conditions that need to be met.
When working with shiftable lines, shifting refers to changing the position of the lines on the graph by adjusting their slope or intercept. The purpose of shifting the lines is often to satisfy certain criteria or align them with specific points or patterns on the graph.
In some cases, achieving the desired outcome may only require shifting one of the lines. This can happen when one line already aligns with the desired points or pattern, and the other line can remain fixed. Moving both lines may not be necessary or could result in an undesired configuration.
However, there are also situations where both lines need to be shifted to achieve the desired result. This can occur when the relationship between the lines or the positioning of the lines relative to the graph requires adjustments to both lines.
Ultimately, the key is to carefully analyze the graph, understand the relationship between the lines, and identify the specific criteria or conditions that need to be met. This analysis will guide the decision of whether one or both lines should be shifted to obtain the correct answer.
Learn more about graph from
https://brainly.com/question/19040584
#SPJ11
find the product of 669 and 83
Answers
The product of 669 and 83 is 55,527
In order to find the product of 669 and 83, we can use the distributive law as shown:
(669)(83)
= (600 + 60 + 9)(80 + 3)
= (600*80) + (600 * 3) + (60*80) + (60*3)+ (9*80) + 9(3)
= 48000 + 1800 + 4800 + 180 + 720 + 27
= 55,527
Hence the product of 669 and 83 is 55,527
Learn more here: https://brainly.com/question/2807928
x = [?]
4x-2 3x + 14
Answers
![x = [?]4x-2 3x + 14](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/FqsBRw16T7nJJQwNqY84ea621Hvjsrpl.png)
The line passing through which two points is parallel to the line x - 2y = 16?
I need help anyone fast please
Answers

can you do this please need it done by midnight
Answers
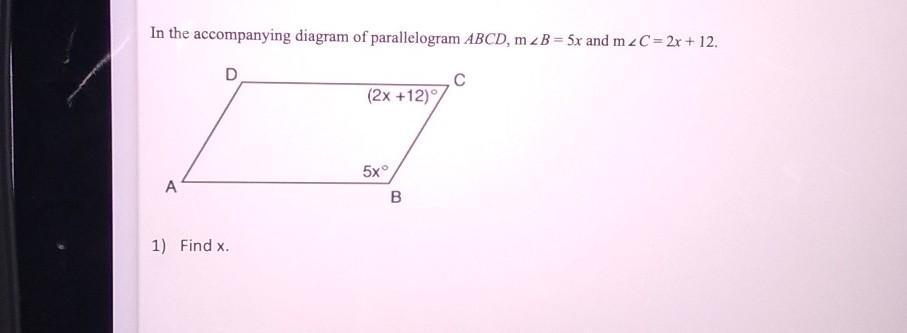
\(\boxed{\pink{\sf\leadsto Value \ of \ x \ is \ 24^{\circ}}}\)
Step-by-step explanation:In the given parallelogram we can see that , <B is 5x° and <C is equal to 2x + 12°.
And these two are co - interior angles . And sum of co - interior angles is 180°.
Hence , here
\(\tt:\implies \angle DCB + \angle ABC = 180^{\circ} \\\\\tt:\implies (2x + 12)^{\circ} + 5x^{\circ}=180^{\circ} \\\\\tt:\implies 7x = (180 - 12 )^{\circ} \\\\\tt:\implies 7x = 168^{\circ} \\\\\tt:\implies x =\dfrac{168^{\circ}}{7} \\\\\underline{\boxed{\red{\tt\longmapsto x = 24^{\circ}}}}\)
Hence the value of x is 24°.\(\rule{200}2\)
What is the difference in the volume of a cylinder having a radius of 4 and a height of 8, and the volume of a rectangular prism having dimensions of length = 10, width = 7 and height = 6? Use 3.14.
Round to the nearest hundredth.
Answers
===========================================
Work Shown:
The cylinder has volume of...
V = pi*r^2*h
V = 3.14*4^2*8
V = 401.92
----------------
The rectangular prism has a volume of...
V = L*W*H
V = 10*7*6
V = 420
----------------
Subtract the two results:
420-401.92 = 18.08
The cylinder has roughly 18.08 more cubic units of volume compared to the rectangular prism.
Answer:
volume of cylinder: V=Sđ*h=R^2*3.14*8
volume of rectangular prism: V=Sđ*h=10*7*6
Please do the calculations yourself for the above 2 calculations
Step-by-step explanation:
WILL MAKE BRAINLIEST HELP
An acute, base Z of an isosceles trapezoid is
eight less than one-third an obtuse, base 2.
Find the measure of an obtuse, base Z.
obtuse base < =
Answers
The measure of the obtuse base Z is -22/3. The given information may lead to a negative value for the measure of the obtuse base, which might not make sense in the context of an isosceles trapezoid.
Let's denote the measure of the obtuse base Z as "x".
According to the given information, the acute base Z of an isosceles trapezoid is eight less than one-third of the obtuse base 2. Mathematically, we can express this relationship as:
Z = (1/3)*2 - 8
Simplifying:
Z = 2/3 - 8
Z = 2/3 - 24/3
Z = -22/3
Therefore, the measure of the obtuse base Z is -22/3.
It's important to note that the given information may lead to a negative value for the measure of the obtuse base, which might not make sense in the context of an isosceles trapezoid. It's possible that there may be an error in the information provided or in the calculations. Please double-check the given information and calculations to ensure accuracy.
Learn more about trapezoid here
https://brainly.com/question/1410008
#SPJ11
when a deck of 52 cards is well shuffled, what is the probability that the four kings are all next to each other and the four queens are all next to each other?
Answers
The probability of four Kings and four Queens being all next to each other in a well shuffled deck of 52 cards is approximately 0.00000000024 or 0.000000002%.
The probability of four Kings being all next to each other in a well shuffled deck of 52 cards is:
(1/51) * (1/50) * (1/49) * (1/48)
= 0.000000000077 or 0.00000077%
The probability of four Queens being all next to each other in a well shuffled deck of 52 cards is:
(1/51) * (1/50) * (1/49) * (1/48)
= 0.000000000077 or 0.00000077%
The probability of four Kings and four Queens being all next to each other in a well shuffled deck of 52 cards is:
0.000000000077 * 0.000000000077
= 0.00000000024 or 0.000000002%
The probability of four Kings and four Queens being all next to each other in a well shuffled deck of 52 cards is very small, approximately 0.00000000024 or 0.000000002%. This is because there are many other combinations of cards that can occur in a shuffled deck.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
suppose you are dealt a 5-card poker hand and your first 2 cards are the two of clubs and two of hearts. how many ways are there to complete your hand such that you end up with no better than a 3 of-a-kind?
Answers
Number of ways there to complete your hand such that you end up with no better than a 3 of-a-kind is 14,212.
There are a total of 47 cards remaining in the deck after you have been dealt the two of clubs and two of hearts. We need to count the number of ways to choose the remaining 3 cards such that we end up with no better than a 3-of-a-kind so we have to use the combinatorics.
We get a pair with one of the two's: There are three remaining two's in the deck, and we need to choose two of them to make a pair. We then need to choose one more card from the remaining 44 cards in the deck that is not the same rank as the pair.
There are (3 choose 2) = 3 ways to choose the pair, and (44 choose 1) = 44 ways to choose the third card. So the total number of ways to complete the hand with a pair of one of the two's is 3 x 44 = 132.
We get three cards of different ranks: We cannot have a pair or three-of-a-kind, so we need to choose three cards of different ranks. There are (12 choose 3) = 220 ways to choose the ranks of the three cards (excluding twos).
For each rank, there are 4 possible cards (one of each suit), so there are (4 choose 1)^3 = 64 ways to choose the three cards of each rank. So the total number of ways to complete the hand with three cards of different ranks is 220 x 64 = 14,080.
Therefore, the total number of ways to complete your hand such that you end up with no better than a 3-of-a-kind is 132 + 14,080 = 14,212.
Learn more about Combinatorics here
brainly.com/question/13266979
#SPJ4