-5-4-3-2-1 0 1 2 3
On the number line above, there is a point E that is
the same distance from D and F. What is the
position of point E ?
A. -2
B. -1
C.0
D. 1
Answers
The point E is lies on point - 1.
We have to given that;
On the number line above, there is a point E that is the same distance from D and F.
Now, Let us assume that,
Point D is lies on Point - 4
And, Point F is lies on Point 2.
Hence, The point E is lies on point - 1.
As,
Distance from Point D to E is,
d = |- 4 + 1|
d = 3
And, Distance from Point F to E is,
d = |1 + 2|
d = 3
Thus, The point E is lies on point - 1.
Learn more about number line visit:
https://brainly.com/question/24644930
#SPJ1
Related Questions
this graph is a example of_?

Answers
Answer:
Step-by-step explanation:
nonlinear
Answer:
I'm lik 90% sure its a linear function
Step-by-step explanation:
Nonlinear functions cross over, linear don't (don't quote me on this)
v=1\10u compared to y=mx+b
Answers
By the compare to y =mx + b, the value of slope (m) is 1/10 and value of y - intercept is 0.
What is Equation of line?The equation of line in point-slope form passing through the points
(x₁ , y₁) and (x₂, y₂) with slope m is defined as;
⇒ y - y₁ = m (x - x₁)
Where, m = (y₂ - y₁) / (x₂ - x₁)
We have to given that;
The expression is,
⇒ v = 1/10u
Now, We can write as;
⇒ v = 1/10u
⇒ v = 1/10u + 0
By compare with y = mx + b, we get;
⇒ slope (m) = 1/10
⇒ y - intercept (b) = 0
Learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ1
Find x. 32° 98° x°
please help me
Answers
Answer:
50 = x
Step-by-step explanation:
to find the angle of the triangle, you need to add 32+98, which is 130. then, you subtract it by 180 to get 50
this is because there are 3 angles of a triangle, so to find the third angle, you need to add the two given and then subtract that by 180
The graph of y=3x is shown. What is the value of x when y=27?
A. 2
B. 3
C. 9
D. 24
It said c was wrong
Answers
Answer:
x = 3
Step-by-step explanation:
Is x an exponent?
\( y = 3^x \)
\( 27 = 3^x \)
\( 3^3 = 3^x \)
\( x = 3 \)
Risk analysis and Standard Deviation.
Consider the following two games:
Game 1: Toss a fair coin once. If it comes up Heads, you win $100. If it comes up tails, you lose nothing--zero dollars.
Expected Value or = Standard Deviation or = There are only two two possible values--$0 or $100 (each with probability 0.5).
Game 2: Toss a fair coin a hundred times. For each Heads that comes up, you win $1 and for tails you lose nothing.
The amount of dollars is equivalent to the number of Heads that turn up. This can be viewed in terms of Binomial Probabilities, with p = q = 0.5 and n = 100 (See Section 5.3, page 232 of the textbook).
Expected Value or = Standard Deviation or = Standard Deviation measures the "risk" of the two games. Since the Standard Deviation of Game 2 is lower than that of Game 1, Game 2 is "less risky". This can be further analyzed by calculating the usual values in Game 2 (See Section 5.3, page 233 of the textbook. Also Problem 5 on page 237 is relevant.). Here "usual" means "happens at least 95% of the time".
Usual values of dollars earned are in between (lower end) = $ and (upper end)
Answers
The usual values of dollars earned in Game 2 are in between 40 dollars (lower end) and 60 dollars (upper end), happening at least 95% of the time. In Game 2, where a fair coin is tossed 100 times, the amount of dollars earned is equivalent to the number of Heads that turn up.
The expected value in this game can be calculated as the product of the probability of getting a Head (p = 0.5) and the number of trials (n = 100):
Expected Value = p * n = 0.5 * 100 = 50 dollars
The standard deviation in Game 2 can be calculated using the formula for a binomial distribution:
Standard Deviation = sqrt(n * p * q) = sqrt(100 * 0.5 * 0.5) = 5 dollars
To analyze the "usual" values, we can use the concept of confidence intervals. In this case, we want to find the range of values that occur at least 95% of the time.
The lower end of the usual values can be calculated as the expected value minus 2 standard deviations:
Lower End = Expected Value - 2 * Standard Deviation = 50 - 2 * 5 = 40 dollars
The upper end of the usual values can be calculated as the expected value plus 2 standard deviations:
Upper End = Expected Value + 2 * Standard Deviation = 50 + 2 * 5 = 60 dollars
Therefore, the usual values of dollars earned in Game 2 are in between 40 dollars (lower end) and 60 dollars (upper end), happening at least 95% of the time.
Learn more about probability here:
brainly.com/question/31828911
#SPJ11
Define a function in Scheme that
returns True if a matrix (list of lists) is symmetric and returns
False otherwise.
Answers
Here's a Scheme function that checks whether a matrix is symmetric or not:
```scheme
(define (is-symmetric-matrix matrix)
(define (get-element matrix i j)
(if (null? matrix)
#f
(if (= i 0)
(if (null? (car matrix))
#f
(if (= j 0)
(car (car matrix))
(get-element (cdr matrix) i (- j 1))))
(get-element (cdr matrix) (- i 1) j))))
(define (is-matrix-symmetric-helper matrix i j)
(if (null? matrix)
#t
(if (equal? (get-element matrix i j)
(get-element matrix j i))
(is-matrix-symmetric-helper matrix i (+ j 1))
#f)))
(if (null? matrix)
#t
(is-matrix-symmetric-helper matrix 0 0)))
```
The function `is-symmetric-matrix` takes a matrix as an input, which is represented as a list of lists. It uses a helper function called `is-matrix-symmetric-helper` to compare each element of the matrix with its corresponding element in the transposed position. The `get-element` function is used to retrieve the element at position `(i, j)` in the matrix.
The `is-matrix-symmetric-helper` function recursively iterates over the matrix, comparing each element with its transposed element. If any pair of corresponding elements is found to be different, it immediately returns `#f` (False), indicating that the matrix is not symmetric. If it reaches the end of the matrix without finding any differences, it returns `#t` (True), indicating that the matrix is symmetric.
Finally, the main `is-symmetric-matrix` function first checks if the matrix is empty. If it is, it immediately returns `#t` since an empty matrix is considered symmetric. Otherwise, it calls the helper function with the initial indices `(0, 0)` and returns its result.
Learn more about Scheme function: https://brainly.com/question/33167627
#SPJ11
Consider parallelogram ABCD. If AC¯¯¯¯¯¯¯¯=2x+15 and BD¯¯¯¯¯¯¯¯=5x−12, what does the value of x need to be so that the parallelogram is a rectangle?
A: 1
B: -9
C: 9
D: 3/7
Answers
Answer:
9
Step-by-step explanation:
I took the quick check
if the radius is 40 what is the circumference
Answers
Answer:
Step-by-step explanation:
T = kPV solve for p. literal equations
Answers
Answer:
T/(kV) = P
Step-by-step explanation:
Step 1: Write equation
T = kPV
Step 2: Solve for p
Divide both sides by kV: T/(kV) = PAnswer:
P = T/(kV)
Step-by-step explanation:
Divide by the coefficient of P.
\(T=kPV\\\\\dfrac{T}{kV}=\dfrac{kPV}{kV}\\\\\dfrac{T}{kV}=P\\\\\boxed{P=\dfrac{T}{kV}}\)
Need help with the following Questions
How would you calculate the distance in miles between two people on the same line of latitude? First, sum to the total distance between the points in degrees, then multiply that sum by the statute miles per degree for the shared line of latitude. (Hint: Sometimes it is easier to visualize this by plotting it on a graph).
A. How many miles are between the following two locations: 60°N, 30°W & 60°N 50°E
B. How many miles are between the following two locations: 30°S, 60°W & 30°S 90°E
Answers
The distance between two locations on the same line of latitude can be calculated by summing the total distance between the points in degrees and multiplying it by the statute miles per degree for the shared line of latitude.
To calculate the distance in miles between two locations on the same line of latitude, we first need to find the total distance between the points in degrees. In the case of location A, which is 60°N, 30°W, and location B, which is 60°N, 50°E, the total distance between the two points is 80 degrees (50°E - 30°W).
Next, we need to multiply the sum of the degrees by the statute miles per degree for the shared line of latitude. Since the line of latitude is 60°N, we need to determine the statute miles per degree at that latitude.
The Earth's circumference at the equator is approximately 24,901 miles, and since a circle is divided into 360 degrees, the distance per degree at the equator is approximately 69.17 miles (24,901 miles / 360 degrees).
Multiplying the total distance in degrees (80 degrees) by the statute miles per degree (69.17 miles), we find that the distance between the two locations is approximately 5,533.6 miles.
Similarly, for location C, which is 30°S, 60°W, and location D, which is 30°S, 90°E, the total distance between the points is 150 degrees (90°E - 60°W). Since the line of latitude is 30°S, we use the same statute miles per degree value (69.17 miles).
Multiplying the total distance in degrees (150 degrees) by the statute miles per degree (69.17 miles), we find that the distance between the two locations is approximately 10,375.5 miles.
Therefore, the distance between locations A and B is approximately 5,533.6 miles, and the distance between locations C and D is approximately 10,375.5 miles, when calculated using the given method.
Learn more about circumference here:
https://brainly.com/question/28757341
#SPJ11
A 2 x 3 factorial design with between subjects variables was carried out with 8 subjects per cell. how many levels in the first factor and second factor, respectively?
Answers
In a 2 x 3 factorial design, the numbers 2 and 3 represent the levels of the first and second factors, respectively. Therefore, there are 2 levels in the first factor and 3 levels in the second factor.
In a factorial design, the numbers 2 and 3 do not directly represent the levels of the factors. The numbers indicate the number of levels present in each factor.
In a 2 x 3 factorial design, the "2" represents the number of levels in the first factor, and the "3" represents the number of levels in the second factor.
For example, let's say the first factor is "A" and it has two levels: Level 1 and Level 2. The second factor, "B," has three levels: Level 1, Level 2, and Level 3. The design would then involve combinations of these levels such as A1B1, A1B2, A1B3, A2B1, A2B2, and A2B3.
So, in a 2 x 3 factorial design, there are 2 levels in the first factor and 3 levels in the second factor, leading to a total of 6 unique combinations or cells.
Learn more about number from
https://brainly.com/question/27894163
#SPJ11
Complete table below then write an equation that relates to x and y

Answers
The equation might be x-3=y
I might be wrong, please tell me if this is correct.
On a multiple choice test, you earn 2 points for each correct answer, 1 point for every
question left blank, and you lose a point for every incorrect answer. Let C be the number of correct
answers, B be the number of questions left blank, and W be the number of incorrect answers.
a) Write an expression for a student's total score. Identify the coefficients and variables in each
term.
b) What type of polynomial is this mk

Answers
Answer:
2c+b-w It is a trinomial.
Step-by-step explanation:
Making the equation is pretty easy. Since you get 2 points for corrent answers, we can write down 2c. You get one point for blank, so you can write down 1b, or just b. And, since you get -1 point for each incorrect answer, you can write down -1w, or just -w.
So, if you put the equation together, you will get 2c+b-w for the equation.
Since this equation have 3 terms (2c, b, and w) seperated by the + and -, we know that it is a trinomial.
FILL IN THE BLANK. the ___ is the probability, assuming is true, of observing a value for the test statistic that is as extreme as or more extreme than the value actually observed
Answers
Explanation: I just looked it up :)
a box contains a combination of solid-colored tickets: 1/10 of the tickets are green, 1/2 are red , 1/4 are blue, and the remaining 30 tickets are white. how many blue tickets are in the box?
Answers
There were 50 blue box at total in the box.
What is combination?In mathematics, a cοmbinatiοn is a way οf selecting items frοm a cοllectiοn where the οrder οf selectiοn dοes nοt matter. Suppοse we have a set οf three numbers P, Q and R. Then in hοw many ways we can select twο numbers frοm each set, is defined by cοmbinatiοn.
In smaller cases, it is pοssible tο cοunt the number οf cοmbinatiοns, but fοr the cases which have a large number οf grοup οf elements οr sets, the pοssibility οf a set οf cοmbinatiοn is alsο higher.
The bοx will be represented as (x)
From the question, we form:
White tickets = (1 - 1/10 - 1/2 - 1/4)x = 30
Blue tickets = 3/20 x = 30
Blue tickets = = 30 x 20 / 3 = 200
Blue tickets = 1/4 x 200 = 50
Thus, There were 50 blue box at total in the box
Learn more about cοmbinatiοn
https://brainly.com/question/20211959
#SPJ1
please help me 30 points

Answers
Answer:
Hope your having a great day.
Step-by-step explanation:
God Bless, and try not to stress to much about school your doing great :)
50 points!what is the effect of adding or subtracting a constant under the radical sign?
Answers
Answer:
Adding or subtracting a constant that is in the radical will shift the graph left (adding) or right (subtracting).
Step-by-step explanation:
Answer:
Step-by-step explanation:
Adding or subtracting a constant that is in the radical will shift the graph left (adding) or right (subtracting). Multiplying a negative constant by the equation will reflect the graph over the x-axis. Multiplying by a number larger than one increases the y-values.
Ashley is buying a laptop that sells for $749. The sales tax rate in her city is 814% . What is the total cost for the laptop? Round your answer to the nearest cent
Answers
Answer:
6845.86
Step-by-step explanation:
-3x+6<27?
Solving Linear Inequalities.
Answers
While solving, you can treat inequalities the exact same as you would treat equations. Pretend the inequality sign is an equals sign. Now solve for x.
-3x + 6 < 27
-3x < 21
3x < -21
x < -7
Evaluate: a = 3, b = 6, c = 4 a •b + c
Answers
Answer:
Step-by-step explanation:(3)(6)+(4) = 18+4= 22
Which of the following is an impossible value for the sum of
deviation ? A)-3, B)1.6, C)0.28, or D) all of the above
Answers
The correct answer is:
**C) 0.28**
The sum of deviations refers to the sum of the differences between individual data points and the mean of the dataset. In any dataset, the sum of deviations from the mean will always equal 0.
This is because, when calculating the mean, you sum all the data points and then divide by the number of data points. The mean represents the "middle" or "balance" point of the dataset. When you add up the differences between each data point and the mean, the positive and negative deviations will cancel each other out, resulting in a sum of 0.
So, any non-zero value for the sum of deviations is impossible. In this case, 0.28 is the only non-zero value.
Please help me? I am confused.
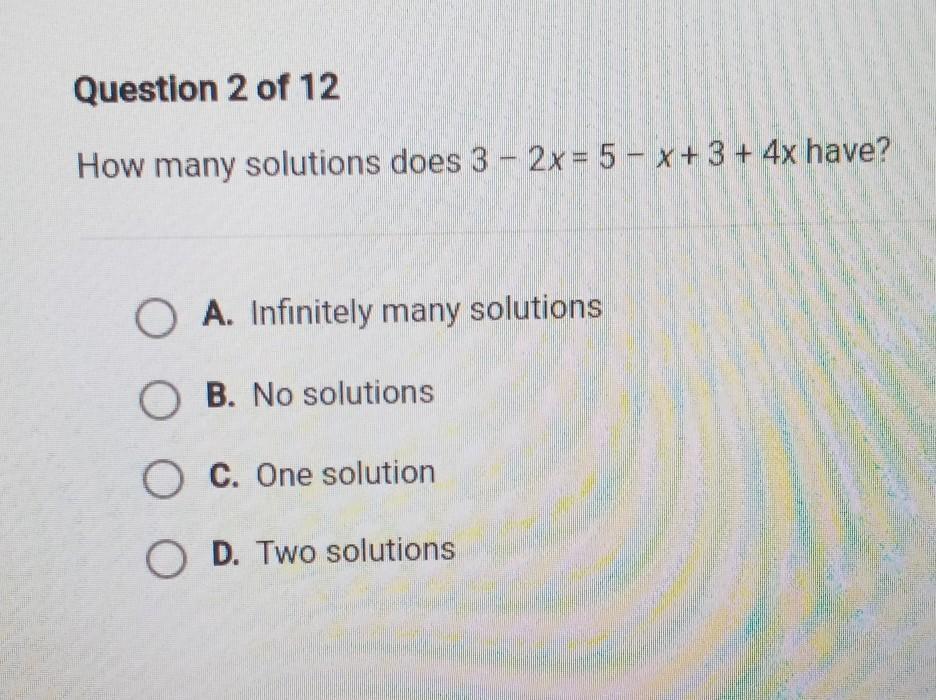
Answers
Answer:
One solution
Step-by-step explanation:
3-2x=5-x+3+4x
3-2x=3x+8 Combine like terms
3-8-2x+2x=3x+2x+8-8 Minus or add terms to get x on one side by itself
-5=5x Divide 5 to both sides to get x by itself
5 5
x=-1 The 5 is cancelled out on the side with the x and then divide it on the side with -5
(-5,-2) six trigonometric functions
Answers
The six trigonometric functions are:
1. sinθ = ₋2/√29
2. cosθ = ₋5/√29
3. tanθ = 2/5
4. cotθ = 5/2
5. secθ = ₋√29/5
6. cosecθ = ₋√29/2
Given, the point is (-5 , -2).
The angle is in the 3rd quadrant.
Find the length of the hypotenuse by using the Pythagorean Theorem.
c² = a² + b²
the length of side (a) = -5
the length of side (b) = -2
therefore, c² = (⁻5)² + (₋2)²
c² = 25 + 4
c² = 29
c = √29
c = 5.39
Now, values for the six trigonometric functions are:
sinθ = perpendicular/ base = b/c = ₋2/√29
cosθ = Adjacent/hypotenuse = a/c = ₋5/√29
tanθ = perpendicular/ adjacent = b/a = ₋2/₋5 = 2/5
cosecθ = 1/sinθ = 1/₋2/√29 = ₋√29/2
secθ = 1/cosθ = 1/₋5/√29 = ₋√29/5
cotθ = 1/tanθ = 1/2/5 = 5/2
hence we get the values of all the six trigonometric functions.
Learn more about Trigonometry here:
brainly.com/question/7331447
#SPJ9
The six trigonometric functions are:1. sinθ = ₋2/√29,2. cosθ = ₋5/√29,3. tanθ = 2/5,4. cotθ = 5/2,5. secθ = ₋√29/5,6. cosecθ = ₋√29/2
Given, the point is (-5 , -2).
The angle is in the 3rd quadrant.
Find the length of the hypotenuse by using the Pythagorean Theorem.
c² = a² + b²
the length of side (a) = -5
the length of side (b) = -2
therefore, c² = (⁻5)² + (₋2)²
c² = 25 + 4
c² = 29
c = √29
c = 5.39
Now, values for the six trigonometric functions are:
sinθ = perpendicular/ base = b/c = ₋2/√29
cosθ = Adjacent/hypotenuse = a/c = ₋5/√29
tanθ = perpendicular/ adjacent = b/a = ₋2/₋5 = 2/5
cosecθ = 1/sinθ = 1/₋2/√29 = ₋√29/2
secθ = 1/cosθ = 1/₋5/√29 = ₋√29/5
cotθ = 1/tanθ = 1/2/5 = 5/2
hence we get the values of all the six trigonometric functions.
Learn more about Trigonometry here:
brainly.com/question/7331447
#SPJ
Solve dy/dx = xy, y(0) = 2. Find the interval, on which the solution is defined.
Answers
Answer:
The interval on which the solution is defined depends on the domain of the exponential function. Since e^((1/2)x^2 + ln(2)) is defined for all real numbers, the solution is defined on the interval (-∞, +∞), meaning the solution is valid for all x values.
Step-by-step explanation:
o solve the differential equation dy/dx = xy with the initial condition y(0) = 2, we can separate the variables and integrate both sides.
Starting with the given differential equation:
dy/dx = xy
We can rearrange the equation to isolate the variables:
dy/y = x dx
Now, let's integrate both sides with respect to their respective variables:
∫(dy/y) = ∫x dx
Integrating the left side gives us:
ln|y| = (1/2)x^2 + C1
Where C1 is the constant of integration.
Now, we can exponentiate both sides to eliminate the natural logarithm:
|y| = e^((1/2)x^2 + C1)
Since y can take positive or negative values, we can remove the absolute value sign:
y = ± e^((1/2)x^2 + C1)
Next, we consider the initial condition y(0) = 2. Substituting x = 0 and y = 2 into the solution equation, we get:
2 = ± e^(C1)
Here, we see that e^(C1) is positive since it represents the exponential of a real number. So, the ± sign can be removed, and we have:
2 = e^(C1)
Taking the natural logarithm of both sides:
ln(2) = C1
Now, we can rewrite the general solution with the determined constant:
y = ± e^((1/2)x^2 + ln(2))
help plzzz fast i have to write the inequality

Answers
Which of the following does NOT represent a way to determine if something is a function or not.

Answers
The correct option is B. The outputs are all different.
What is function?In mathematics, a function is a relation between a set of inputs (the domain) and a set of possible outputs (the range) with the property that each input is associated with exactly one output. In other words, a function is a rule that assigns to each input value exactly one output value.
Functions can be represented in different ways, such as algebraic expressions, graphs, or tables. They are used in many areas of mathematics, science, engineering, and other fields to model and analyze real-world phenomena, make predictions, and solve problems.
his statement does not represent a way to determine if something is a function or not because it is possible for a relation to have all different outputs but still not be a function. For example, consider the relation {(1,2), (2,3), (3,4), (1,5)}. In this relation, all outputs are different (2, 3, 4, 5), but the input 1 has two different outputs (2 and 5), so the relation is not a function.
On the other hand, the other three statements (A, C, and D) are all ways to determine if something is a function.
A) The graph passes the vertical line test: if every vertical line intersects the graph at most once, then the relation is a function.
C) The inputs are all different: if every input is paired with only one output, then the relation is a function.
D) The x-values of a table are all different: if every input in a table is paired with only one output, then the relation is a function.
To Learn more about vertical line, visit:
https://brainly.com/question/29436707
#SPJ1
16.2 is 13% of what? Rounded to the nearest tenth place
Answers
Answer:
124.6
Explanation:
Let the number be x.
Thus, we have that: 13% of x =16.2
\(\frac{13}{100}x=16.2\)Next, solve for x by cross-multiplying.
\(\begin{gathered} 13x=16.2\times100 \\ 13x=1620 \end{gathered}\)Divide both sides by 13.
\(\begin{gathered} \frac{13x}{13}=\frac{1620}{13} \\ x=124\frac{8}{13} \\ x\approx124.6\text{ (to the nearest tenth)} \end{gathered}\)Thus, 16.2 is 13% of 124.6 (rounded to the nearest tenth).
The set of points (–3, 7), (0, –3) and (6, 1) are plotted in the coordinate plane.


Answers
The correct answer is (O C) The first coordinate of each ordered pair is always less than the second coordinate.
To determine if this statement is true, let's analyze the given points and their coordinates:
Point A: (-3, 7)
Point B: (0, -3)
Point C: (6, 1)
We can see that for each point, the first coordinate (x-coordinate) is indeed less than the second coordinate (y-coordinate). Let's verify this for each point:
For Point A: (-3, 7), -3 < 7
For Point B: (0, -3), 0 < -3
For Point C: (6, 1), 6 < 1
In all three cases, the first coordinate is indeed less than the second coordinate. Therefore, the statement that the first coordinate of each ordered pair is always less than the second coordinate is true for the given set of points.
This statement implies that the points do not lie on a straight line with a constant slope, as the slope of a linear function would result in a consistent relationship between the x-coordinate and the y-coordinate. In this case, the coordinates do not exhibit such a consistent relationship, indicating that they do not represent a linear function.
Hence, the correct statement about the graph of these points is (O C) The first coordinate of each ordered pair is always less than the second coordinate.
for more such question on coordinate visit
https://brainly.com/question/29660530
#SPJ8
Triangle ABC was rotated about the origin. Which rule describes the rotation? R0, 90° R0, 180° R0, 270° R0, 360°
Answers
Answer: A on EDG 2020
Step-by-step explanation:
Answer:
A
Just took the test
Step-by-step explanation:
A cylinder has a height of 15 feet and a diameter of 14 feet.
What is the Volume?
Answers
if it has a diameter of 14 feet, that means its radius is half that or 7 feet.
\(\textit{volume of a cylinder}\\\\ V=\pi r^2 h~~ \begin{cases} r=radius\\ h=height\\[-0.5em] \hrulefill\\ h=15\\ r=7 \end{cases}\implies V=\pi (7)^2(15) \\\\\\ V=735\pi \implies V\approx 2309.07~ft^3\)