Bob's gift shop sold a record number of cards for Mother's Day. One salesman sold 36 cards, which was 20% of the cards sold for Mother's Day. How many cards were sold for Mother's Day? Multiply/scale up to solve. cards percent 36 20 100
Answers
Answer:
180 cards
Step-by-step explanation:
If one sales person sold 36 cards, which was 20% of the total cards sold, then the total number of cards sold for Mother's Day was 36 / 0.20 = <<36/0.20=180>>180 cards.
Thus, a record number of 180 cards were sold for Mother's Day at Bob's gift shop.
Answer:
Step-by-step explanation:36=20%=0.2
y/s=y/s
36=y/s
20=y/s
100=y/s
Related Questions
Translate: the sum of 4 and a number (x)
Answers
Answer:
9
Step-by-step explanation:
4 + x =9
Have a great day
Natalie invests $2,000 into a savings account
which earns 11% per year. In 20 years, how
much will Natalie's investment be worth if
interest is compounded monthly? Round to the
nearest dollar.
Answers
Answer:
We can use the formula for compound interest to find the future value (FV) of Natalie's investment:
FV = P * (1 + r/n)^(n*t)
Where:
P is the principal amount (the initial investment), which is $2,000 in this case
r is the annual interest rate as a decimal, which is 11% or 0.11
n is the number of times the interest is compounded per year, which is 12 since interest is compounded monthly
t is the number of years, which is 20
Substituting the values into the formula, we get:
FV =
2
,
000
∗
(
1
+
0.11
/
12
)
(
12
∗
20
)
�
�
=
2,000 * (1.00917)^240
FV = $18,255.74
Therefore, after 20 years of compounded monthly interest at a rate of 11%, Natalie's investment of 2,000 will be worth approximately 18,256.
Answer:
$17,870
Step-by-step explanation:
You must use the formula for compound interest.
A = P(1 + r/n)^nt
I suggest you look it up at some point so that you can do these more easily in the future!
FRERŔ PIOINTS ANSWER QUICK
FP FP ANSWER QUICK FOR FP
Answers
Explanation:
The table below shows the earnings, in thousands of dollars, for three different commissioned employees.
Employee #1
$2,000 + 3% on all sales
Employee #2
7% on all sales
Employee #3
5% on the first $40,000 + 8% on anything over $40,000
December
4.4
5.6
5.2
January
3.5
3.85
3.6
February
4.7
4.9
4.4
Which employee did not have the same dollar amount in sales for the month of February as the other two employees?
a.
Employee #1.
b.
Employee #2
c.
Employee #3
d.
They each had the same dollar amount in sales.
Answers
The employee who did not have the same dollar amount in sales for the month of February as the other two employees is (a) Employee 1.
What is Percentage?Percentage is defined as the parts of a number per fraction of 100. We have to divide a number with it's whole and then multiply with 100 to calculate the percentage of any number.
Earnings of three employees in the month of February are :
Employee 1 = 4.7 = $4700
Employee 2 = 4.9 = $4900
Employee 3 = 4.4 = $4400
Earnings of employee 1 = $2,000 + 3% on all sales
Let the amount of all sales be x.
2000 + (3% x ) = 4700
2000 + 0.03x = 4700
0.03x = 2700
x = 90,000
Earnings of employee 2 = 7% on all sales
Let the amount of all sales be x.
0.07x = 4900
x = $70,000
Earnings of employee 3 = 5% on the first $40,000 + 8% on anything over $40,000
Let the amount of sales be 40,000 + x.
(0.05 × 40,000) + (0.08 x) = 4400
2000 + 0.08x = 4400
0.08x = 2400
x = $30,000
Amount of sales = $40,000 + $30,000 = $70,000
Hence employee 1 did not have the same amount as the other 2 in February.
Learn more about Percentage here :
https://brainly.com/question/1811849
#SPJ5
Does -a ? = (-a)?? Explain why or why not.
Answers
Explanation:
Always remember that variables have coefficients (x is the same as 1·x or 1x).
Raising a base to either an odd or even exponent has particular rules when it comes to signs:
If you raise -a² = -a² because a has a coefficient of - 1. This implies that -a² = -1a². Now, raising -a³ (odd exponent) still results in -a³ because you're only raising the base, a, to its exponent, and it doesn't include its coefficient of -1. Hence, -a³ = -1a³ = -a³.Also, (-a²) = -a² because once again, you're only raising the base, a, and not its coefficient (even if both are inside the parenthesis).It will be different if the base is raised as follows:
(-a)² = a² because the coefficient, -1, is included within the parenthesis. It is the same as (-1a)² = 1a² or a².(-a)³ = -a³ or -1a³ because it is an odd exponent, and if you raise a negative base to an odd exponent results in a negative value of the base.The key is that the exponent outside the parenthesis will affect both the coefficient and its base, such as (-a)².
Hope this makes complete sense.
Data was collected for a sample of organic snacks. The amount of sugar (in mg) in each snack is
summarized in the histogram below.
What is the sample size for this data set?

Answers
Explanation:
Add up the heights of each bar to get the sample size.
4+4+7+12+11+4+1 = 43
alondra is starting a college savings account. She has already saved $400. she devises a periodic savings plan with a monthly deposit to save $7,000 in 3 years as shown

Answers
According to the data, Alondra would have to save $275 each month if she wants to have $7,000 after two years.
How to calculate how much Alondra must save to have $7,000 after 2 years?To calculate the savings that Alondra must make to have $7,000 after 2 years we must carry out the following procedure:
First, we must subtract $400 from her initial contribution to your savings.
$7,000 - $400 = $6,600
Then we must divide $6,600 into the number of months that are 2 years (24 months).
$6,600 / 24 = $275
Based on the above, if she saves $275 of her salary each month, she will have $7,000 after 2 years. This is possible because her monthly payment is $358.41
Learn more about savings at: https://brainly.com/question/30004719
#SPJ1
Find the of the slope of the line through (6,-10) and (4,-8)
Answers
Answer:
-1
Step-by-step explanation:
y = mx + c
m is the slope/gradient
to find slope = y2 - y1 / x2 - x1
= -8 - -10 / 4 - 6
m = -1
6. Mrs. Ramirez' groceries cost $50 before tax, and the total including sales tax was $55. What is
the sales tax rate that Mrs. Ramirez paid?
Answers
Answer:sales tax rate would be 0.1
using the formula
Sales tax rate = Sales tax percent / 100
The photo is kinda blurry but please help me with it

Answers
The perimeter of rectangle M'N'O'P' is given as follows:
54 cm.
What is a dilation?A dilation can be defined as a transformation that multiplies the distance between every point in an object and a fixed point, called the center of dilation, by a constant factor called the scale factor.
The ratio between the areas is given as follows:
126/14 = 9.
The area is measure in square units, while the perimeter is measured in units, hence the ratio of the perimeters is the square root of the ratio of the areas, that is:
3.
Hence the perimeter of rectangle M'N'O'P' is given as follows:
3 x 18 = 54 cm.
Missing InformationThe complete problem is:
Rectangle MNOP has a perimeter of 18 cm and an area of 14 cm2. After rectangle MNOP is dilated, rectangle M'N'O'P' has an area of 126 cm2. What is the perimeter of rectangle M'N'O'P'?
More can be learned about dilation at brainly.com/question/3457976
#SPJ1
ASAP!!! Please help me solve

Answers
Answer: j(x) = (x-1)(x+2)
The x-1 part is because of the root x = 1
The root x = -2 leads to the factor x+2
Need some help 54 pts

Answers
Step-by-step explanation:
as shown in the picture.
you can comment if there is a problem

A student was asked to give the exact solution to the equation
22x+4-9(2) = 0
The student's attempt is shown below:
22x+49(2)=0
22x+24-9(2) = 0
Let 2* = y
y²-9y+8=0
(y-8)(y-1)=0
y = 8 or y=1
So x = 3 or x = 0
(a) Identify the two errors made by the student.
(b) Find the exact solution to the equation.
Answers
(a) The errors made by the student are:
Incorrectly expanding 49(2) as 24 instead of 98.
Mistakenly factoring the quadratic equation as (y - 8)(y - 1) instead of
\(y^{2} - 9y + 8.\)
(b) The exact solution to the equation is x = 7/11.
(a) The student made two errors in their solution:
Error 1: In the step \("22x + 49(2) = 0,"\) the student incorrectly expanded 49(2) as 24 instead of 98. The correct expansion should be 49(2) = 98.
Error 2: In the step \("y^{2} - 9y + 8 = 0,"\) the student mistakenly factored the quadratic equation as (y - 8)(y - 1) = 0. The correct factorization should be \((y - 8)(y - 1) = y^{2} - 9y + 8.\)
(b) To find the exact solution to the equation, let's correct the errors made by the student and solve the equation:
Starting with the original equation: \(22x + 4 - 9(2) = 0\)
Simplifying: 22x + 4 - 18 = 0
Combining like terms: 22x - 14 = 0
Adding 14 to both sides: 22x = 14
Dividing both sides by 22: x = 14/22
Simplifying the fraction: x = 7/11
Therefore, the exact solution to the equation is x = 7/11.
For more questions on quadratic equation
https://brainly.com/question/30164833
#SPJ8
Can you construct a triangle with side lengths of 1 meter, 7 meters, and 8 meters?
Yes or no and explain
Answers
Answer:
No.
Step-by-step explanation:
No.
Each side of a triangle must have a length between the difference and the sum of the lengths of the other two sides.
Let's look at the sum and difference of lengths of 2 sides.
Side with length 1 and side with length 7; third side with length 8
sum of lengths of first two sides = 1 + 7 = 8
difference = 7 - 1 = 6
The third side would have to have a length between 6 and 8. The third side has a length of 8. For a triangle, the third side must be between the sum and difference. Here, the third side is equal to the sum, so there is no triangle.
As soon as one side does not work, there is no triangle, and you don't need to check the sums and differences of the other two sets of two sides.
d/4-9=-3
Type only the number for "d".
Answers
d/4-9=3
d/4=12
d=48
hope this helps! :D
PLEASE HELP LAST THING I NEED ON MATH
WILL GIVE BRAINLIEST, THANKS AND 5* VOTE
TROLL = WILL GET ALL THEIR ANSWERS AND QUESTIONS REPORTED

Answers
Answers:
side a = 12.3 unitsangle B = 100 degreesside b = 15.8 units===========================================================
Explanation:
Let A = 50 degrees and C = 30 degrees. The side opposite angle uppercase C is lowercase c = 8. Convention usually has uppercase letters as the angles, while the lowercase letters are side lengths. A goes opposite 'a', B goes opposite b, and C goes opposite c.
Let's use the given angles to find the missing angle B
A+B+C = 180
50+B+30 = 180
B+80 = 180
B = 180-80
B = 100
Now we can apply the law of sines to find side b
b/sin(B) = c/sin(C)
b/sin(100) = 8/sin(30)
b = sin(100)*8/sin(30)
b = 15.7569240481953
b = 15.8
Make sure your calculator is in degree mode.
----------------------------
We'll do the same thing to find side 'a'
a/sin(A) = c/sin(C)
a/sin(50) = 8/sin(30)
a = sin(50)*8/sin(30)
a = 12.2567110899037
a = 12.3
Both values for 'a' and b are approximate (even before rounding).
-----------------------------
Extra info (optional)
As you can probably tell or guess, the phrasing "solve the triangle" means "find all sides and angles".Notice how if we erase the question marked sides and angles of the original drawing, we're left with something in the AAS case. Meaning that exactly one triangle is possible here. We don't have to worry about any ambiguous case.If you wanted, you could apply the law of cosines rule after you determine two sides and an included angle between them. This will yield the length of the side opposite the angle.Answer:
B=100
b=15.7
a=12.25
Step-by-step explanation:
first find the missing angle:
B=180-50-30
B=100
then use the law of sines:
\( \frac{a}{ \sin(a) } = \frac{b}{ \sin(b) ) } = \frac{c}{ \sin(c) } \)
then
\( \frac{a}{ \sin(50) } = \frac{8}{ \sin(30) } \\ \\ a = 12.25\)
use the same way to find the other side
\( \frac{b}{ \sin(100) } = \frac{8}{ \sin(30) } \\ b = 15.7\)
What is the slope of a line parallel to the line whose equation is 6x -2y= 32. Fully simplify your answer
Answers
Step-by-step explanation:
Given equation is
6x -2y= 32.........i)
Slope of line I) is
\(m1 = \frac{ - x \: coefficient}{y \: coefficient} \\ = \frac{ - 6}{ - 2} \\ = 3\)
Now
As it is said that the lines are parallel so slope, m1 = m2
So the slope of a line parallel to line I) is
= 3
Hope it will help :)❤
The lengths of a particular animal's pregnancies are approximately normally distributed, with mean μ=257 days and standard deviation a = 8 days.
(a) What proportion of pregnancies lasts more than 267 days?
(b) What proportion of pregnancies lasts between 255 and 261 days?
(c) What is the probability that a randomly selected pregnancy lasts no more than 245 days?
(d) A "very preterm baby is one whose gestation period is less than 239 days. Are very preterm babies unusual?
Answers
a. It should be noted that about 10.56% of pregnancies last more than 267 days.
b. It should be noted that about 26.76% of pregnancies last between 255 and 261 days.
c. The probability that a randomly selected pregnancy lasts no more than 245 days is about 6.68%.
d. Only about 1.22% of pregnancies are extremely preterm, a somewhat uncommon event.
How to explain the probabilityIn this case, to see, to see if very preterm babies are uncommon, we must compare the likelihood of a pregnancy lasting less than 239 days to some criterion. We can employ the z-score:
z = (239 - 257) / 8 = -2.25
To the left of 239, there is:
P(X < 239) = P(Z < -2.25) = 0.0122
This suggests that only about 1.22% of pregnancies are extremely preterm, a somewhat uncommon event. As a result, very premature newborns are considered rare.
Learn more about probability on
https://brainly.com/question/24756209
#SPJ1
a. It should be noted that about 10.56% of pregnancies last more than 267 days.
b. It should be noted that about 26.76% of pregnancies last between 255 and 261 days.
c. The probability that a randomly selected pregnancy lasts no more than 245 days is about 6.68%.
d. Only about 1.22% of pregnancies are extremely preterm, a somewhat uncommon event.
How to explain the probabilityIn this case, to see, to see if very preterm babies are uncommon, we must compare the likelihood of a pregnancy lasting less than 239 days to some criterion. We can employ the z-score:
z = (239 - 257) / 8 = -2.25
To the left of 239, there is:
P(X < 239) = P(Z < -2.25) = 0.0122
This suggests that only about 1.22% of pregnancies are extremely preterm, a somewhat uncommon event. As a result, very premature newborns are considered rare.
Learn more about probability on
https://brainly.com/question/24756209
#SPJ1
Ronald scores 700 on the math section of the SAT exam. The distribution of SAT scores is approximately normal with a mean of 500 and a standard deviation of 100. Rubin takes the ACT math exam and scores 31 on the math portion. ACT scores are approximately normally distributed with a mean of 18 and a standard deviation of 6.7
(a) Relative to their peers who also took the tests, who performed better on his test? Explain.
(b) A certain school will only consider those students who score in the top 1% in the math section. What grades would Ronald and Rubin have to receive on their respective tests to be considered for admission?
(c) Between what two grades does 95% of the population fall for the ACT and the SAT exams?
Answers
Answer:
a) Due to the higher z-score, Ronald performed better relative to his peers on the test.
b) Ronald needed a grade of at least 732.5, and Rubin of at least 33.58.
c) 95% of the population fall between graded of 4.868 and 31.132 on the ACT.
95% of the population fall between graded of 304 and 696 on the SAT.
Step-by-step explanation:
Normal probability distribution
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question:
(a) Relative to their peers who also took the tests, who performed better on his test? Explain.
We have to find whoever has the higher z-score.
Ronald:
Ronald scores 700 on the math section of the SAT exam. The distribution of SAT scores is approximately normal with a mean of 500 and a standard deviation of 100. So the z-score is found when \(X = 700, \mu = 500, \sigma = 100\). So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{700 - 500}{100}\)
\(Z = 2\)
Rubin:
Rubin takes the ACT math exam and scores 31 on the math portion. ACT scores are approximately normally distributed with a mean of 18 and a standard deviation of 6.7. So the z-score is found when \(X = 31, \mu = 18, \sigma = 6.7\). So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{31 - 18}{6.7}\)
\(Z = 1.94\)
Due to the higher z-score, Ronald performed better relative to his peers on the test.
(b) A certain school will only consider those students who score in the top 1% in the math section. What grades would Ronald and Rubin have to receive on their respective tests to be considered for admission?
They have to be in the 100 - 1 = 99th percentile, that is, they need a z-score with a pvalue of at least 0.99. So we need to find for them X when Z = 2.325.
Ronald:
\(Z = \frac{X - \mu}{\sigma}\)
\(2.325 = \frac{X - 500}{100}\)
\(X - 500 = 232.5\)
\(X = 732.5\)
Rubin:
\(Z = \frac{X - \mu}{\sigma}\)
\(2.325 = \frac{X - 18}{6.7}\)
\(X - 18 = 15.58\)
\(X = 33.58\)
Ronald needed a grade of at least 732.5, and Rubin of at least 33.58.
(c) Between what two grades does 95% of the population fall for the ACT and the SAT exams?
They fall between the 100 - (95/2) = 2.5th percentile and the 100 + (95/2) = 97.5th percentile, that is, they fall between X when Z = -1.96 and X when Z = 1.96.
ACT:
Lower bound:
\(Z = \frac{X - \mu}{\sigma}\)
\(-1.96 = \frac{X - 18}{6.7}\)
\(X - 18 = -1.96*6.7\)
\(X = 4.868\)
Upper bound:
\(Z = \frac{X - \mu}{\sigma}\)
\(1.96 = \frac{X - 18}{6.7}\)
\(X - 18 = 1.96*6.7\)
\(X = 31.132\)
95% of the population fall between graded of 4.868 and 31.132 on the ACT.
SAT:
Lower bound:
\(Z = \frac{X - \mu}{\sigma}\)
\(-1.96 = \frac{X - 500}{100}\)
\(X - 500 = -196\)
\(X = 304\)
Upper bound:
\(Z = \frac{X - \mu}{\sigma}\)
\(1.96 = \frac{X - 500}{100}\)
\(X - 500 = 196\)
\(X = 696\)
95% of the population fall between graded of 304 and 696 on the SAT.
One month Sam rented 3 movies and 5 video games for a total of $32. The next month, he rented 12 movies and 2 video games for a total of $29. Find the rental cost for a movie and a video game.
Answers
Using a system of equations, the rental cost for a movie and a video game is as follows:
Movie = $1.50Video game = $5.50.What is a system of equations?A system of equations is two or more equations solved concurrently or at the same time.
A system of equations is also described as simultaneous equations.
Movies Video Total
Games Cost
First month rental 3 5 $32
Second month rental 12 2 $29
Let the rental cost per movie = x
Let the rental cost per video game = y
Equations:
3x + 5y = 32 ... Equation 1
12x + 2y = 29 ... Equation 2
Multiply Equation 1 by 4:
12x + 20y = 128 ... Equation 3
Subtract Equation 2 from Equation 3:
12x + 20y = 128
-
12x + 2y = 29
18y = 99
y = 5.5
Substitute y = 5.5 in Equation 1 or 2:
12x + 2y = 29
12x + 2(5.5) = 29
12x + 11 = 29
12x = 18
x = 1.5
Thus, based on simultaneous equations, the rental cost for a movie is $1.50 while a video game's is $5.50.
Learn more about simultaneous equations at https://brainly.com/question/16863577.
#SPJ1
76%
Here are ten numbers:
3 7 2 4 7 5 7 1 8 8
a) Write down the mode.
b)
Work out the median.
c)
Calculate the mean.
d)
What is the range?
Answers
Answer:
Mode = 7
Median = 6
Mean = 5.2
Range = 7
Step-by-step explanation:
Mode:
The most repeated number is 7 (thrice).
Median:
First, arrange them in order.
1, 2, 3, 4, 5, 7, 7, 7, 8, 8
The two middle numbers are 5 and 7. Find their average.
(5 + 7)/2 = 6
Mean:
(3+7+2+4+7+5+7+1+8+8)/10 = 5.2
Range:
Largest number - smallest number
8 - 1 = 7
Hope this helps!
Thank you for taking the time out of your day to help me. Appreciate it.

Answers
The features of the sine function are given as follows:
Amplitude of 2.
Period of π/2.
Phase shift of π/8 units left
Vertical shift of 1. (translation up one unit).
Hence the equation is:
y = 2sin(4(x - π/8)) + 1.
How to define the sine function?The standard definition of the sine function is given as follows:
y = Asin(B(x - C)) + D.
For which the parameters are given as follows:
A: amplitude.
B: the period is 2π/B.
C: phase shift.
D: vertical shift.
The maximum value of the function is of 3, and the minimum is of -1, for a difference of 4, hence the amplitude is given as follows:
2A = 4
A = 2.
With no vertical shift, the function should oscillate between -2 and 2, but it oscillates between -1 and 3, hence the vertical shift is given as follows:
D = 1.
The shortest distance between repetitions is of π/4 - (-π/4), meaning that the period is of π/2, and thus the coefficient B is given as follows:
2π/B = π/2
2/B = 1/2
B = 4.
The function crosses it's midline at x = π/8, hence the phase shift is of π/8 units left, meaning that the coefficient C is given as follows:
C = -π/8.
Hence the function is of:
y = 2sin(4(x - π/8)) + 1.
More can be learned about trigonometric functions at brainly.com/question/21558626
#SPJ1

Question 2 Rewrite in simplest radical form 1 x −3 6 . Show each step of your process.

Answers
Answer:
√(x)
Step-by-step explanation:
(1)/(x^-(1/2)) that's 3 goes into -3 leaving 1 and goes into 6 leaving 2
1/2 is same as 2^-1
so therefore we can simplify the above as
x^-(-1/2)
x^(1/2)
and 4^(1/2)
is same as √(4)
so we conclude as
√(x)
Rylon Corporation manufactures Brute and Chanelle perfumes. The raw materials needed to manufacture each type of perfume can be purchased for $3 per pound. Processing 1 lb of raw material requires 1 hour of laboratory time. Each pound of processed raw material yields 3 oz of Regular Brute Perfume and 4 oz of Chanelle perfume. Regular Brute can be sold for $7/oz and Regular Chanelle for $6/oz. Rylon also has the option of further processing Regular Brute and Regular Chanelle to produce Luxury Brute, sold at $18/oz, and Luxury Chanelle, sold at $14/oz. Each ounce of Regular Brute processed further requires an additional 3 hours of laboratory time and $4 processing cost and yields 1 oz of Luxury Brute. Each ounce of Regular Chanelle processed further requires an additional 2 hours of laboratory time and $4 processing cost and yields 1 oz of Luxury Chanelle. Each year, Rylon has 6,000 hours of laboratory time available and can purchase up to 4,000 lb of raw material. Question : what is the simplex algorithm (manual table ) to find a solution to the linear programming problem given above
Answers
Convert the problem to standard form and write the initial tableau with slack variables:
Maximize
\(Z = 7*3 + 6*4 + 18*5 + 14*6 - 3*1 - 3*2 - 4*5 - 4*6\)
Subject to:
\(x1 + x2 + s1 = 4000\\x3 - (1/3)*1 + (1/3)*5 = 0\\x4 - (1/3)*2 + (1/2)*6 = 0\\x3*1 + 3*2 + 3*3 + 3*4 + 3*5 + 2*6 + s2 = 6000\)
All variables are non-negative.
Tableau
x1 x2 x3 x4 x5 x6 s1 s2 b
Z -3 -3 7 6 18 14 0 0 0
s1 1 1 0 0 0 0 1 0 4000
s2 3 3 3 3 3 2 0 1 6000
x5 0 0 1 0 1/3 0 0 0 0
x6 0 0 0 1 0 1/2 0 0 0
The basic variables are s1, s2, x5, and x6.
Step 1: Choose entering variable. The most positive coefficient in objective row is 18, corresponding to x5. x5 enters the basis.
Step 2: Choose the leaving variable. The minimum ratio of right-hand side to coefficient of x5 is 12000/(1/3) = 36000,
corresponding to s1. s1 leaves the basis.
Step 3: Perform, pivot operation to make x5 the basic variable for s1. Divide, pivot row by 1/3 and subtract appropriate multiples of the pivot row from other rows to make other entries in column 5 zero.
x1 x2 x3 x4 x5 x6 s1 s2 b
Z -3 -3 7 6 18 14 0 0 0
x5 0 0 1 0 1/3 0 0 0 0
s2 3 3 3 3 2 2/3 2/3 0 1/3 24000
x3 1 0 1/3 0 1/3 0 -1/3 0 0
x4 0 1 0 1/3 0 1/2 -1/6 0 0
The basic variables are x5, x3, x4, and s2.
Step 4: Choose the entering variable. The most positive coefficient in the objective row is 7, corresponding to x3. x3 enters the basis.
Step 5: Determine the leaving variable. The right-hand side's minimum ratio to the coefficient of x3 is 0, indicating that x3 can be increased without bound. This implies that the optimal solution is unbounded and that there is no finite optimal value for the problem.
As a result, the simplex algorithm demonstrates that the given linear programming problem lacks a feasible solution. This means that it is not possible to meet all of the constraints at the same time.
For more question on simplex algorithm click on
https://brainly.com/question/29554333
#SPJ4
Three boxes are stacked one on top of the other. One box is 4 feet 8 inches tall, one is 3 feet 10 inches tall, and one is 2 feet 7 inches tall. How high is the stack?
Write your answer in feet and inches. Use a number less than 12 for inches.
Answers
If the odds against an event are 3:5, then the probability that the event will fail to occur is
Answers
Answer:
3/8
Step-by-step explanation:
probability = wanted outcomes / total outcomes
odds = wanted outcomes / unwanted outcomes
Odds of 3:5 losing means 3 losing outcomes and 5 winning outcomes.
The total outcomes is 8
The probability of losing which is the probability that the event will fail to occur is 3/8.
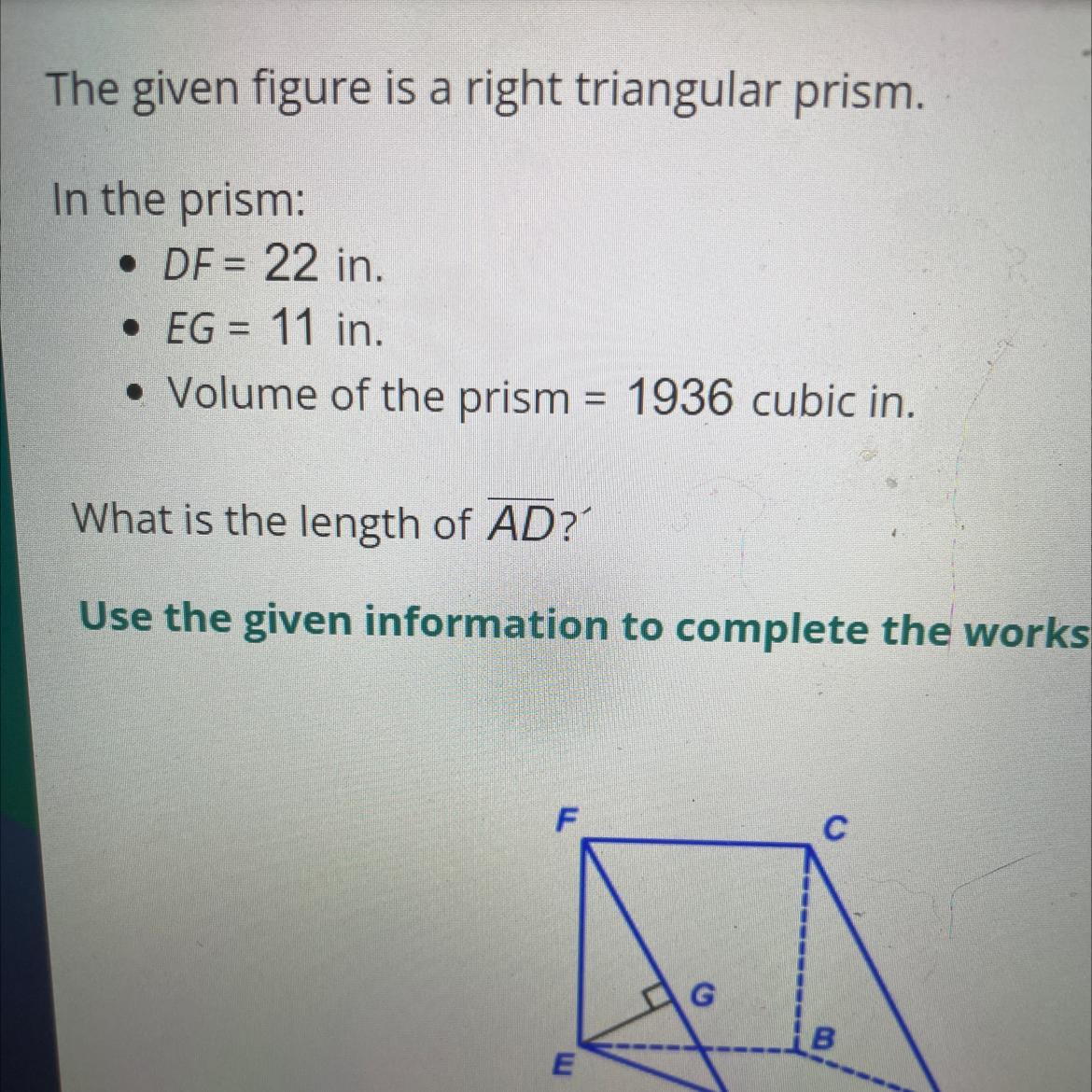
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
Find the missing side lengths, put answer as radical in simplest form
Look at picture for reference

Answers
The value of the missing side lengths x and y are 5√2 and 5 respectively.
What is the value of side length x and y?The figure in the image is a right triangle.
Angle θ = 45 degree
Hypotenuse = x
Opposite to angle θ = y
Adjacent to angle θ = 5
To solve for side x and side y, we use the trigonometric ratio.
Note that:
Cosine = adjacent / hypotenuse
tangent = opposite / adjacent
Solving for x:
Cosine = adjacent / hypotenuse
Plug in the values
cos( 45 ) = 5/x
x = 5 / cos( 45 )
x = 5√2
Solving for side y:
tangent = opposite / adjacent
Plug in the values
tan( 45 ) = y/5
y = tan( 45 ) × 5
y = 5
Therefore, the value of side length x is 5 units.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
what is the equivalent fraction of 13%
Answers
What is the solution to the system of equations graphed below?
y = 3x + 2
5
y = -2x - 3

Answers
Answer:
-2, 1 i'm very positivee