Begin by graphing the absolute value function, f(x)= |x|. Then use transformations of this graph to graph the given function h(x)=-|x-4|What transformations are needed in order to obtain the graph of h(x) from the graph of f(x)? Select all that apply

Answers
SOLUTION
To answer the question correctly, let us look at the graph of the function and the graph of the image.
The graph function
\(f\mleft(x\mright)=|x|\)is
The graph of the image function
\(h\mleft(x\mright)=-|x-4|\)is
Looking at both graphs, we can seee that
1. There is a reflection of the original function over the x-axis
2. You can see a shift from point (0, 0) of the original funtion to a point (4, 0) of the image function.
Hence, the answers are
B. Horizontal shift and
F. Reflection about the x-axis


Related Questions
Question is in the picture
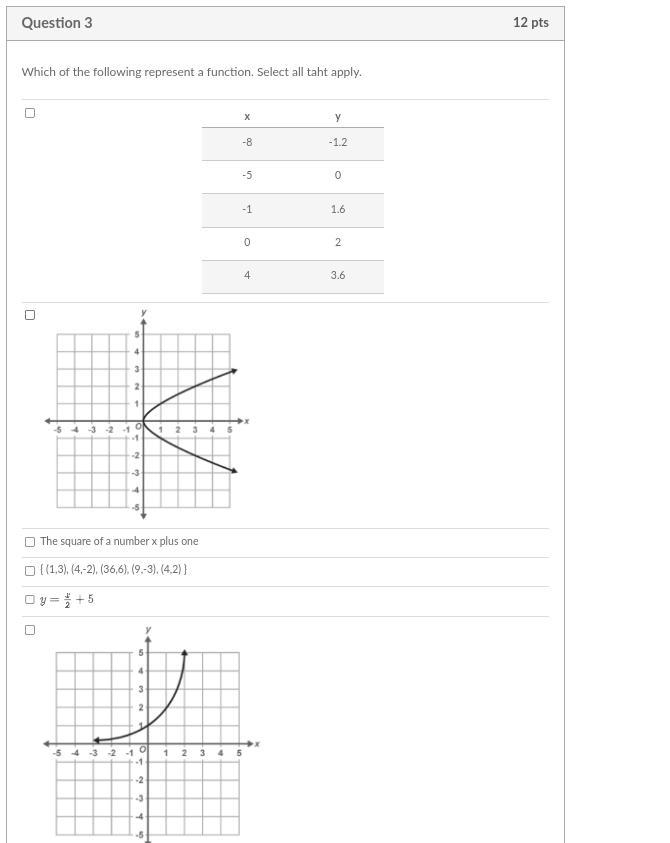
Answers
The relations that represent functions are given as follows:
Table.The square of a number x plus one.y = x/2 + 5.Graph at the bottom.When does a relation represents a function?A relation represents a function when each input value is mapped to a single output value.
Hence the two items that are not functions in this problem are given as follows:
Graph -> second item -> vertically aligned points for x > 0, meaning that the values of x > 0 are mapped to two values of y.The set of ordered pairs, as the input of 4 is mapped to outputs of -2 and 2.More can be learned about relations and functions at brainly.com/question/10283950
#SPJ1
enter the number to complete the linear combination.after substitution:gcd(85, 51) yields sequence: 85 51 34 17 0
Answers
The Greatest Common Divisor (GCD) of 85 and 51 is 17.
Greatest Common Divisor(GCD)The greatest common factor that divides two or more numbers is known as the greatest common divisor (GCD). The highest common factor is another name for it (HCF).
Explanation
Step 1: Divide 85 by 51. The quotient is 1 and the remainder is 34.
Step 2: Divide 51 by 34. The quotient is 1 and the remainder is 17.
Step 3: Divide 34 by 17. The quotient is 2 and the remainder is 0.
Step 4: Since the remainder is 0, the Greatest Common Divisor (GCD) of 85 and 51 is 17.
The GCD of 85 and 51 is 17.
To know more about GCD visit here:
https://brainly.com/question/5252620
#SPJ4
A Best Buy Store is having a Black friday sake. After a 20% reduction, Sarah bought a Ps4 for $316.00 - what was the original Price of the ps4?
Answers
Answer:
20% + 100% = 120% therefore ( 316x120% ) ÷ 100 = 379.2 = original price
Question provided in attachment.

Answers
We can be 99% confident that the true mean healing rate of newts falls within the interval of 22.919 to 30.415 micrometers per hour.
How to calculate the valueSample Mean: = (29 + 27 + 34 + 40 + 22 + 28 + 14 + 35 + 26 + 35 + 12 + 30 + 23 + 18 + 11 + 22 + 23 + 33) / 18
= 480 / 18
≈ 26.667
Sample Standard Deviation (s):
= ✓((Σ(29 - 26.667)² + (27 - 26.667)² + ... + (33 - 26.667)²) / (18 - 1))
≈ ✓(319.778 / 17)
≈ ✓(18.81)
≈ 4.336
Confidence level = 99%
Sample Size (n) = 18
Sample Mean = 26.667
Sample Standard Deviation (s) = 4.336
Degrees of Freedom (df) = n - 1 = 18 - 1 = 17
Using a t-table or statistical software, we find that the critical value for a 99% confidence level with 17 degrees of freedom is approximately 2.898.
Margin of Error (E) = 2.898 * (4.336 / ✓18))
≈ 3.748
Confidence Interval = (26.667 - 3.748, 26.667 + 3.748)
= (22.919, 30.415)
We can be 99% confident that the true mean healing rate of newts falls within the interval of 22.919 to 30.415 micrometers per hour. This means that if we were to repeat the study multiple times and construct confidence intervals, approximately 99% of those intervals would contain the true mean healing rate of the population.
Learn more about confidence interval on
https://brainly.com/question/15712887
#SPJ1
A rectangular tank 80 cm wide by 100 cm long by 60 cm high is filled up with water up to of its height. Water is then poured into the tank until it is 3 filled with 384 € of water. Find the amount of water that was poured the tank. Give your answer in litres.
Answers
Answer:
0 liters
Step-by-step explanation:
The first step in solving this problem is to find the volume of water that was originally in the tank when it was filled up to of its height. Since the tank is rectangular, we can use the formula for the volume of a rectangular prism:
Volume of tank = length x width x height = 100 cm x 80 cm x 30 cm = 240,000 cm³
Since the tank was filled up to of its height, the volume of water in the tank at this point is:
Volume of water in tank = 100 cm x 80 cm x 30 cm x 0.5 = 1,200,000 cm³
To find the amount of water that was poured into the tank to fill it up to 3 of its height, we need to subtract the volume of water that was originally in the tank from the total volume of water when it is 3 filled, which is 384 liters or 384,000 cm³ (since 1 liter = 1000 cm³):
Volume of water poured into tank = Volume of water when 3 filled - Volume of water in tank at of its height
= 384,000 cm³ - 1,200,000 cm³
= -816,000 cm³
Wait a minute, this result is negative, which means there was no water poured into the tank to reach the 3 filled level. In fact, it suggests that there was an excess of water that had to be removed from the tank to reach the desired level. This could be because the dimensions of the tank were not exact or because the tank was not level when filled to the first level.
Therefore, the answer to the problem is 0 liters or 0 cm³.
Note: It is important to always check the result of a calculation to ensure it makes sense in the context of the problem. In this case, the negative volume of water poured into the tank indicates that there may be an error in the problem statement or in the measurements provided.
?
0.07
What is 70 x 10^2
Answers
Answer:
7000
Step-by-step explanation:
I think this is the answer
Find the perimeter and area of the sector for the figure shown in white, to three significant figures.
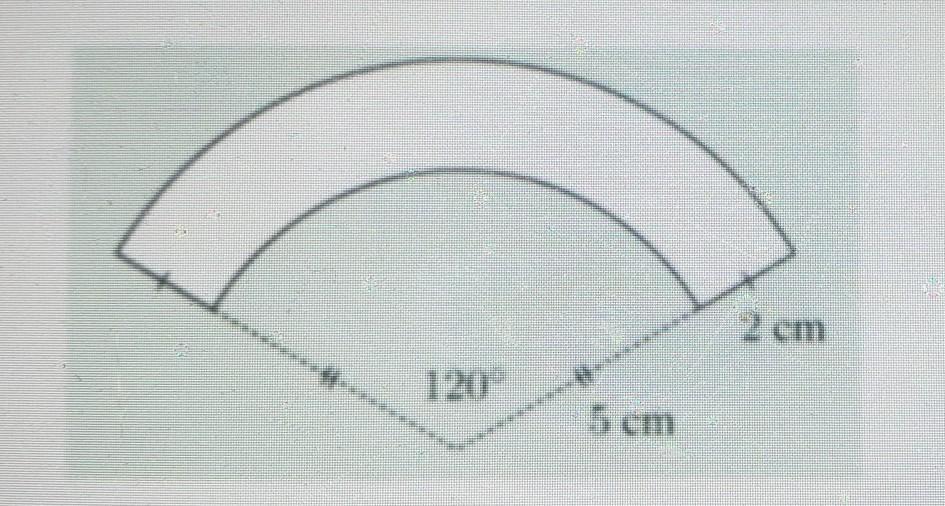
Answers
The area of a circle is computed as follows:
\(A=\pi\cdot r^2\)If the radius is 7 cm, then the area is:
\(A=\pi\cdot7^2=153.938\text{ sq. cm}\)If the radius is 5 cm, then the area is:
\(A=\pi\cdot5^2=78.539\text{ sq. cm}\)Then, the area of the "ring" made by the subtraction of a circle of a radius of 5 cm to a circle of a radius of 7 cm is:
153.938 - 78.539 = 75.399 sq. cm
In the picture of the problem, we see a part of this "ring". The whole area computed before corresponds to an angle of 360°, to calculate the area that corresponds to 120° we can use the next proportion:
\(\begin{gathered} \frac{75.399\text{ sq. cm}}{x\text{ sq. cm}}=\frac{360\text{ \degree}}{120\text{ \degree}} \\ \frac{75.399}{x}=3 \\ \frac{75.399}{3}=x \\ 25.133\text{ sq. cm= x} \end{gathered}\)The perimeter of a circle is computed as follows:
\(P=2\cdot\pi\cdot r\)If the radius is 7 cm, then the perimeter is:
\(P=2\cdot\pi\cdot7=43.982\text{ cm}\)Given that 120° is 1/3 of a circle, then the length of the top arc is:
1/3*43.982 = 14.66 cm
If the radius is 5 cm, then the perimeter is:
\(P=2\cdot\pi\cdot5=31.415\text{ cm}\)Given that 120° is 1/3 of a circle, then the length of the bottom arc is:
1/3*31.415 = 10.471 cm
Then, the perimeter of the figure is:
14.66 + 10.471 + 2 + 2 = 29.131 cm
the cost of the food that was originally 300 php was reduced to 180 php. what was the percent of the reduction
Answers
Answer: 60% of 300 is 180
What is the slope of y = -x + 7?
Answers
Answer:
-1
Step-by-step explanation:
y = mx + b
m = slope
b = y-intercept
y = -x + 7
m = -1
The ratio of students with blond
hair to students with brown or
black hair is 1:2. If there are
212 students with brown or black
hair, how many students have
blond hair?
Answers
Answer: 106 students
Step-by-step explanation:
In a 1:2 ratio, we can see that there are 2x the amount of students with brown/black hair compared to students with blonde hair.
So taking 212 students, we can divide the number by half to get 106 students.
\(\frac{212}{2} = 106\)
Our department store is having a sale on personal computers, of which three are in stock (no rain checks). There is a certain probability of selling none. The probability of selling one is twice as great as the probability of selling none. The probability of selling two is three times the probability of selling none. Finally, the probability of selling all the personal computers is four times as great as the probability of selling none. Finally, the probability of selling all the personal computers is four times as great the probability of selling none. In a table list the outcomes and their probabilities.
Answers
Answer:
Following are the solution to the given question:
Step-by-step explanation:
Let the possibility including its sale will be x
Purchases possibility for \(1=2x\)
Purchases possibility for \(2=3x\)
Purchases possibility for \(3= 4x\)
Calculating the total possibility \(=x+2x+3x+4x=10x\)
The total possibility within the framework of the sample=1
\(\to 10x =1\\\\\to x = \frac{1}{10}\\\\\to x = 0.1 \\\\\)
\(Outcome \ \ \ \ \ \ \ \ \ \ Probability\\\\0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0.1\\\\1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0.2\\\\2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0.3\\\\3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0.4\\\)
The wheels on noah’s bike have a circumference of about 5 feet how many time do the wheels rotated if noah rides 40 feet
Answers
Step by step
If the wheel is 5 feet around, we can divide the 40 feet by the 5 feet per rotation, = 8 rotations

The starting point of a function is called the
Answers
Geoff works at a warehouse, earning $17.50 per hour plus a $200 one-time hiring bonus. In Geoff's first week, his pay including the bonus was $637.50.
Write and solve an equation to find how many hours, h, Geoff worked his first week.
Answers
Answer:
Geoff worked 25 hours in his first week
Step-by-step explanation:
You would subtract $200 from $637.50 which makes it $437.50. Then you would divide $437.50 by $17.50 which is 25, This means that Geoff worked 25 hours in his first week.
The following bar chart shows the distances run by Jay's family in a race.
Find the median distance in km.

Answers
The median of the distances is M = 6.5 kilometers
Given data ,
To find the median of a set of numbers, we arrange the numbers in ascending order and then locate the middle value. If there is an odd number of values, the median is the middle number. If there is an even number of values, the median is the average of the two middle numbers.
Arranging the given set of numbers in ascending order: {4, 5, 8, 11}
Since the set has an even number of values, the median is the average of the two middle numbers. In this case, the two middle numbers are 5 and 8. To find the average, we add these two numbers and divide by 2:
(5 + 8) / 2 = 13 / 2 = 6.5
Hence , the median of the given set {4, 5, 8, 11} is 6.5
To learn more about median click :
https://brainly.com/question/28687994
#SPJ1
does x*x*x*x*x = 5x?
I'm not really sure so it would help.
Answers
Answer:
Step-by-step explanation:
no ,x*x*x*x*x=x^5
x+x+x+x+x=5x
in multiplication those who have same base we add their power.
in addition those variables which have same base(or are like term) we add them.
The distance between Point P and Point Q was 3600 m. Beng Leong started jogging
at 08 35 from Point P and reached Point Q at 08 50. At the same time, Sam started
jogging from Point P at a speed of 200 m/min. Who jogged at a faster speed?
How much faster was his speed?
Answers
Answer:
Ben ran at a speed of 240m/min and Sam ran at a speed of 200m/min So Ben is faster by a rate of 40/min
Step-by-step explanation:
Ben's miles per minutes
\( \frac{3600}{15} = 240\)
Sam's miles per minute
Given
50 points. use rotation tool in top right to flip upright.

Answers
Answer:
(a) 56%
(b) 28%
Step-by-step explanation:
Hope this helps! :)
The graph shows a proportional relationship. Which equation matches the graph? A: y=1/3x B: y=x C: y=3x D: y=9x

Answers
The equation that represent the graph is C) y=3x.
What is equation?
The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign.
Here let us take the two points \((x_1,y_1)=(1,3) , (x_2,y_2)=(3,9)\).
Now using slope formula then,
=> slope m = \(\frac{y_2-y_1}{x_2-x_1}\)
=> m = \(\frac{9-3}{3-1}=\frac{6}{2}=3\).
Now using equation formula then,
=> \(y-y_1=m(x-x_1)\)
=> y-3=3(x-1)
=> y-3 = 3x-3
=> y=3x.
Hence the equation that represent the graph is C) y=3x.
To learn more about equation refer the below link
https://brainly.com/question/29336774
#SPJ9
Plane JMP and plane KLO what is it
Answers
Question 2 of 10 The graphs below have the same shape. What is the equation of the blue graph? f(x) = x2 g(x) = 2 foy 6 -5 g(x) = O A. g(x) = (x - 5)2

Answers
Notice that both graphs have the same shape, but the blue curve is the red one after a translation to the right.
In general, given a function h(x), a translation in the x-axis direction is given by the formula
\(\begin{gathered} h(x)\to h(x-a) \\ a>0\to\text{ a units to the right} \\ a<0\to\text{ a units to the left} \end{gathered}\)In our case, notice that the vertex of the parabola (0,0) transforms into (5,0)
\(\begin{gathered} (0,0)\to)=(5,0)=(5+0,0) \\ \Rightarrow g(x)=f(x-5) \end{gathered}\)Then,
\(\Rightarrow g(x)=(x-5)^2\)The answer is g(x)=(x-5)^2
Swornima is an unmarried nurse in a
hospital. Her monthly basic salary is Rs
48,000. She has to pay 1% social
security tax on her income up to Rs
5,00,000 and 10% income tax on Rs
5,00,001 to Rs 7,00.000. She gets 1
months' salary as the Dashain
allowance. She deposits 10% of her
basic salary in Citizen Investment Trust
(CIT) and gets 10% rebate on her
income tax. Answer the following
questions. (i) What is her annual
income? How much tax is rebated to
her? (iii) How much annual income tax
should she pay?
Answers
To calculate Swornima's annual income and the amount of tax she should pay, let's break down the information provided:
Monthly basic salary: Rs 48,000
Social security tax rate: 1%
Income tax rate on income up to Rs 5,00,000: 0% (no tax)
Income tax rate on income from Rs 5,00,001 to Rs 7,00,000: 10%
Dashain allowance: 1 month's salary
Deposit in Citizen Investment Trust (CIT): 10%
Rebate on income tax: 10%
(i) Annual Income:
Swornima's monthly basic salary is Rs 48,000, so her annual basic salary would be:
Annual Basic Salary = Monthly Basic Salary x 12
= Rs 48,000 x 12
= Rs 5,76,000
Additionally, she receives 1 month's salary as the Dashain allowance, which we can add to her annual income:
Annual Income = Annual Basic Salary + Dashain Allowance
= Rs 5,76,000 + Rs 48,000
= Rs 6,24,000
Swornima's annual income is Rs 6,24,000.
(ii) Tax Rebate:
Swornima receives a 10% rebate on her income tax. To calculate the rebate, we need to determine her income tax first.
(iii) Annual Income Tax:
First, let's calculate the income tax for the range of income from Rs 5,00,001 to Rs 7,00,000. The tax rate for this range is 10%.
Taxable Income in this range = Rs 6,24,000 - Rs 5,00,000
= Rs 1,24,000
Income Tax in this range = Taxable Income x Tax Rate
= Rs 1,24,000 x 0.1
= Rs 12,400
Now, let's calculate the total annual income tax:
Total Annual Income Tax = Income Tax in the range Rs 5,00,001 to Rs 7,00,000
= Rs 12,400
Next, we calculate the rebate on income tax:
Tax Rebate = Total Annual Income Tax x Rebate Rate
= Rs 12,400 x 0.1
= Rs 1,240
Swornima's annual income tax is Rs 12,400, and she receives a tax rebate of Rs 1,240.
To summarize:
(i) Swornima's annual income is Rs 6,24,000.
(ii) Swornima's tax rebate is Rs 1,240.
(iii) Swornima should pay an annual income tax of R
11 13 Which angles form a linear pair?
PRL and LRM
ORP and MRN
MRN and NRO
LRP and ORP
dont mind what was selected in the photo
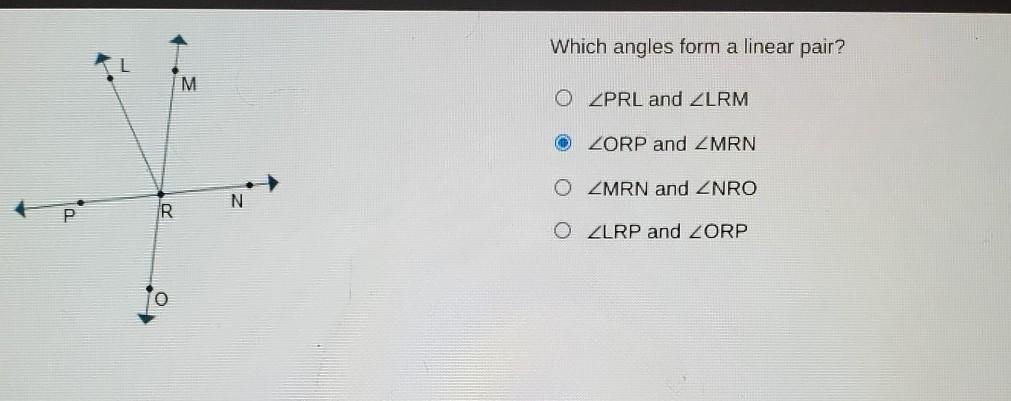
Answers
Answer:
< MRN and < NRO
Step-by-step explanation:
Recall that angles which forma linear pair ae those whose addotion gives 180 degrees (a line).
So in our case these are: < MRN and < NRO
Terry and Jim have two car loans totaling $ 26,004.
One loan has an annual percentage rate (APR) of 3.1 % and the other has an APR of 7%.
If the total interest they paid after one year is $1,481.25, what is the amount owed on each car?
(1 = PRT. Note t = 1 year).
Answer needed right away!! With explanation
Answers
The annual percentage rate is the interest rate for payment for the car
loan.
The mount owed on the car with an APR of 3.1% is approximately $8,693.08.The mount owed on the car with an APR of 7% is approximately $17,310.92.The given parameters are;
The amount of loan Terry and Jim have = $26,004
The annual percentage rate (APR) on one loan = 3.1 %
The annual percentage rate (APR) on the other loan = 7 %
Total interest paid after one year = $1,481.25
Required:
The amount owed on each car
Solution:
Let X represent the loan, with 3.1% APR, we have;
The other loan with 7% APR = 26,004 - X
Therefore;
0.031·X + 0.07·(26,004 - X) = 1,481.25
0.031·X + 1,820.28 - 0.07·X = 1,481.25
1,820.28 - 1,481.25 = 0.07·X - 0.031·X = 0.039·X
339.03 = 0.039·X
\(X = \dfrac{339.03}{0.039} \approx 8693.08\)Therefore;
The amount owed on the car with an APR of 3.1%, X ≈ $8,693.08Therefore;
The amount owed on the car with an APR of 7% ≈ 26,004 - 8693.08 =
17310.92.
The amount owed on the car with an APR of 7% ≈ $17,310.92Learn more here:
https://brainly.com/question/15400760
If you reflect the triangle below over the x-axis, what quadrant would it be in?

Answers
The correct answer is Quadrant 4, that is, the last option.
The concept of best-, worst-, and average-case analyses extends beyond algorithms to other counting problems in mathematics. Recall that the height of a binary tree is the number of edges in the longest path from the root to a leaf. Find the best-case height of a binary tree with seven nodes.
Answers
the height of a binary tree is the number of edges in the longest path from the root to a leaf.The best-case height of a binary tree with seven nodes is 3.
A binary tree is a type of tree structure consisting of nodes that are connected by edges. The number of edges in the longest path from a binary tree's root to a leaf determines the tree's height.In the best-case scenario, the binary tree is perfectly balanced and each node has exactly two children. With seven nodes, the best-case height is three because each node has two children and three edges connect the root node to the leaves. This means that the longest path from the root to a leaf is three edges, resulting in a height of three.
Learn more about binary tree here
https://brainly.com/question/28391940
#SPJ4
Carla earns $564 for 30 hours of work. Which represents the unit rate?
a) $30 per hour
b) $168 per hour
c) $18.80 per hour
d) $5.30 per hour
Answers
13х-17y+16z= 73
-11x + 15y + 17z= 61
46x+10y-30z = -18
Answers
The solution of the linear system of three simultaneous equations is presented as follows; x = 2, y = 1 and z = 4
What is a set of simultaneous equation?Simultaneous system of equations consists of a finite set of equations for which a solution to the equation system is required.
The linear system of three equations can be presented as follows;
13•x - 17•y + 16•z = 73...(1)
-11•x + 15•y + 17•z = 61...(2)
46•x + 10•y - 30•z = -18...(3)
The above system of equations can be solved using common multiples of the coefficients as follows;
Multiply equation (2) by 2 and equation (3) by 3 to get;
2 × (-11•x + 15•y + 17•z) = 2 × 61 = 122
-22•x + 30•y + 34•z = 122...(4)3 × (46•x + 10•y - 30•z) = 3 × (-18) = -54
138•x + 30•y - 90•y = -54...(5)Subtracting equation (4) from equation (5) gives;
138•x + 30•y - 90•z - (-22•x + 30•y + 34•z) = -54 - 122 = -176
138•x - (-22•x) + 30•y - 30•y - 90•z - 34•z = -176
160•x - 124•z = -176
40•x - 31•z = 44
\( \displaystyle {z = \frac{(44 + 40\cdot x)}{31}}\)
Plugging in the value of z in equation (1) and (2) gives;
1043•x - 527•y + 704 = 73 × 31 = 2236...(6)
Which gives;
\( \displaystyle {y = \frac{(1043\cdot x - 1559)}{527}}\)
339•x + 465•y + 748 = 61 × 31 = 1891...(7)
Which gives; \( \displaystyle {y = \frac{(381 - 113\cdot x )}{155}}\) which gives;
\( \displaystyle { \frac{(1043\cdot x - 1559)}{527}= \frac{(381 - 113\cdot x )}{155}}\)
Therefore; 221216•x - 442432 = 0
x = 442432 ÷ 221216 = 2
x = 2
y = (1043×2 - 1559)÷527 = 1
y = 1
z = (44 + 40×2) ÷ 31 = 4
z = 4
Learn more about linear system of equations here:
https://brainly.com/question/25098653
#SPJ1
2(cos^4 60 +sin^4 30) -(tan^2 60 +cot^2 45) +3*sec^2 30
Answers
The value of the expression \(2(cos^4 60 + sin^4 30) -(tan^2 60 + cot^2 45) + 3\times sec^2 30 is 33/4.\)
Let's simplify the expression step by step:
Recall the values of trigonometric functions for common angles:
cos(60°) = 1/2
sin(30°) = 1/2
tan(60°) = √(3)
cot(45°) = 1
sec(30°) = 2
Substitute the values into the expression:
\(2(cos^4 60 + sin^4 30) - (tan^2 60 + cot^2 45) + 3sec^2 30\)
= \(2((1/2)^4 + (1/2)^4) - (\sqrt{(3)^2 + 1^2} ) + 3(2^2)\)
= 2(1/16 + 1/16) - (3 + 1) + 3*4
= 2(1/8) - 4 + 12
= 1/4 - 4 + 12
= -15/4 + 12
= -15/4 + 48/4
= 33/4
Therefore, the value of the expression \(2(cos^4 60 + sin^4 30) -(tan^2 60 + cot^2 45) + 3\times sec^2 30 is 33/4.\)
for such more question on expression
https://brainly.com/question/4344214
#SPJ8
Please help me with this.

Answers
Here are the correct matches to the expressions to their solutions.
The GCF of 28 and 60 is 4.
(-3/8)+(-5/8) = -4/4 = -1.
-1/6 DIVIDED BY 1/2 = -1/6 X 2 = -1/3.
The solution of 0.5 x = -1 is x = -2.
The solution of 1/2 m = 0 is m = 0.
-4 + 5/3 = -11/3.
-2 1/3 - 4 2/3 = -10/3.
4 is not a solution of -4 < x.
1. The GCF of 28 and 60 is 4.
The greatest common factor (GCF) of two numbers is the largest number that is a factor of both numbers. To find the GCF of 28 and 60, we can factor each number completely:
28 = 2 x 2 x 7
60 = 2 x 2 x 3 x 5
The factors that are common to both numbers are 2 and 2. The GCF of 28 and 60 is 2 x 2 = 4.
2. (-3/8)+(-5/8) = -1.
To add two fractions, we need to have a common denominator. The common denominator of 8/8 and 5/8 is 8. So, (-3/8)+(-5/8) = (-3 + (-5))/8 = -8/8 = -1.
3. -1/6 DIVIDED BY 1/2 = -1/3.
To divide by a fraction, we can multiply by the reciprocal of the fraction. The reciprocal of 1/2 is 2/1. So, -1/6 DIVIDED BY 1/2 = -1/6 x 2/1 = -2/6 = -1/3.
4. The solution of 0.5 x = -1 is x = -2.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate x by dividing both sides of the equation by 0.5. This gives us x = -1 / 0.5 = -2.
5. The solution of 1 m = 0 is m = 0.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate m by dividing both sides of the equation by 1. This gives us m = 0 / 1 = 0.
6. -4 + 5/3 = -11/3.
To add a fraction and a whole number, we can convert the whole number to a fraction with the same denominator as the fraction. In this case, we can convert -4 to -4/3. So, -4 + 5/3 = -4/3 + 5/3 = -11/3.
7. -2 1/3 - 4 2/3 = -10/3.
To subtract two fractions, we need to have a common denominator. The common denominator of 1/3 and 2/3 is 3. So, -2 1/3 - 4 2/3 = (-2 + (-4))/3 = -6/3 = -10/3.
8. 4 is not a solution of -4 < x.
The inequality -4 < x means that x must be greater than -4. The number 4 is not greater than -4, so it is not a solution of the inequality.
For more such questions on GCF
https://brainly.com/question/902408
#SPJ8