based on what you know about the empirical rule and z-scores, and assuming a normal distribution, what is the approximate percentile rank of a value that is associated with a z-score of 0?
Answers
According to the empirical rule, z-scores, and supposing a normal distribution, a number with a z-score of 0 has an estimated percentile rank of 50.
Define the term empirical rule in normal distribution?A statistical principle known as the empirical rule, also known as the three rule or 68-95-99.7 rule, holds that with a normal distribution, mostly all observed data will lie around three standard deviations (signified by σ ) of the mean or average (signified by µ ).
In accordance with the Empirical Rule, 99.7% of data that are found to have a normal distribution fall around 3 standard deviations from the mean.According to this formula, 68% of the data are within one standard deviation of the mean, 95% are within two deviations, and 99.7% are within three standard deviations.Thus, as per the empirical rule, z-scores, and supposing a normal distribution, a number with a z-score of 0 has an estimated percentile rank of 50.
To know more about the empirical rule, here
https://brainly.com/question/28873888
#SPJ4
Related Questions
Lines and are parallel lines cut by a transversal. Use the lines and the angles formed to select all that are true statements. Select 3 correct answer(s)
a. Angle 3 and Angle 6 are vertical angles.
b. Angle 1 and Angle 5 are corresponding angles.
c. Angle 6 and Angle7 are vertical angles.
d. Angle 7 and angle 8 are supplementary angles.
e. Angle 2 and angle 4 are alternate interior angles.
f. Angle 1and angle 4 are same side interior angles.
Answers
The corrrect statements about angle are:
Angle 1 and angle 5 are corresponding anglesAngle 6 and angle 7 are vertical anglesAngle 7 and angle 8 are supplementary anglesPlease refer to the attached picture below for visualization of the angles.
Based on the attached picture, we can consider the relationship of each angle, such as:
Alternate interior angles and congruent:
Angle 4 and angle 5
Angle 3 and angle 6
Alternate exterior angles and congruent:
Angle 1 and angle 8
Angle 2 and angle 7
Consecutive interior angles and supplementary:
Angle 3 and angle 5
Angle 4 and angle 6
Corresponding angles and congruent:
Angle 1 and angle 5
Angle 2 and angle 6
Angle 3 and angle 7
Angle 4 and angle 8
Vertical angles and congruent:
Angle 1 and angle 4
Angle 2 and angle 3
Angle 5 and angle 8
Angle 6 and angle 7
Supplementary angles:
Angle 1 and angle 2
Angle 3 and angle 4
Angle 5 and angle 6
Angle 7 and angle 8
Learn more about Angle here: brainly.com/question/28451077
#SPJ4

Find the solution of the following differential equation by Laplace transforms with initial conditions for each equation: a) y" – y = t y(0) = 1, y'(0) = 1 b) y" + y' = t² + 2t y(0) = 4, y'(0) = -2 c) d²y/dt⁴ + d³y/dt³ = cost y(0) = y'(0) = y"' (0) = 0, y" (0) = 1
Answers
Laplace transforms are an essential mathematical tool used to solve differential equations. These transforms transform differential equations to algebraic equations that can be solved easily.
To solve the differential equations given in the question, we will use Laplace transforms. So let's start:Solution:a) y" – y = t y(0) = 1, y'(0) = 1First, we take the Laplace transform of the given differential equation.L{y" - y} = L{ty}
Taking the Laplace transform of both sides gives:L{y"} - L{y} = L{ty}Using the formula, L{y"} = s²Y(s) - s*y(0) - y'(0), and L{y} = Y(s) then we get:s²Y(s) - s - 1 = (1/s²) + (1/s³)Rearranging the above equation, we get:Y(s) = [1/(s²*(s² + 1))] + [1/(s³*(s² + 1))]Now, we apply the inverse Laplace transform to find the solution.y(t) = (t/2)sin(t) + (cos(t)/2)
The solution of the differential equation y" – y = t, with initial conditions y(0) = 1, y'(0) = 1 is y(t) = (t/2)sin(t) + (cos(t)/2).
To know more about Laplace transforms visit
https://brainly.com/question/30759963
#SPJ11
x = −1 and y = −1 perpendicular or parellel
Answers
Answer:
aaaaaaaaaaaaaaaaaaaaaa
aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
Step-by-step explanation:
4. Find and simplify the curl and divergence of \( \boldsymbol{F}(x, y, z)=\frac{x}{y^{2}} \boldsymbol{i}+\frac{y^{2}}{z} j+\frac{x^{2}}{z^{2}} \boldsymbol{k} \) \( [8 \) points]
Answers
To calculate the curl and divergence of a given vector field \(\(\vec F(x,y,z)\)\)
that is defined as:
\(\( \boldsymbol{F}(x, y, z)=\frac{x}{y^{2}} \boldsymbol{i}+\frac{y^{2}}{z} j+\frac{x^{2}}{z^{2}} \boldsymbol{k} \)\),
we will use the following Curl and Divergence formulas.
The Curl of a vector field is given by
\(\[\nabla \times \vec{F}=\left(\frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z}\right) \vec{i}+\left(\frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x}\right) \vec{j}+\left(\frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y}\right) \vec{k}\]\)
And the Divergence of a vector field is given by
\(\[\nabla \cdot \vec{F}=\frac{\partial F_{x}}{\partial x}+\frac{\partial F_{y}}{\partial y}+\frac{\partial F_{z}}{\partial z}\]\)
Let us begin by computing the curl of\(\(\vec{F}\)\) using the formula above.
\(\[\begin{aligned} \nabla \times \vec{F} &=\left(\frac{\partial}{\partial y}\left(\frac{x}{y^{2}}\right)-\frac{\partial}{\partial z}\left(\frac{y^{2}}{z}\right)\right) \vec{i}+\left(\frac{\partial}{\partial z}\left(\frac{x}{y^{2}}\right)-\frac{\partial}{\partial x}\left(\frac{x^{2}}{z^{2}}\right)\right) \vec{j}+\left(\frac{\partial}{\partial x}\left(\frac{y^{2}}{z}\right)-\frac{\partial}{\partial y}\left(\frac{x^{2}}{z^{2}}\right)\right) \vec{k} \\ &=\left(-\frac{x}{y^{3}}\right) \vec{i}\end{aligned}]\)\(+\left(\frac{2 x}{z}-\frac{2 x}{z}\right) \vec{k} \\ &=\left(-\frac{x}{y^{3}}\right) \vec{i}+\left(\frac{2 x}{z^{2}}-\frac{y^{2}}{z^{2}}\right) \vec{j}+\vec{0} \end{aligned}\]\)
Next, we will compute the divergence of\(\(\vec F\)\)using the formula above.
\(\[\begin{aligned} \nabla \cdot \vec{F} &=\frac{\partial}{\partial x}\left(\frac{x}{y^{2}}\right)+\frac{\partial}{\partial y}\left(\frac{y^{2}}{z}\right)+\frac{\partial}{\partial z}\left(\frac{x^{2}}{z^{2}}\right) \\ &=\frac{1}{y^{2}}+\frac{2 y}{z^{3}}-\frac{2 x^{2}}{z^{3}} \\ &=\frac{z^{3}+2 y^{3}-2 x^{2} y^{2}}{y^{2} z^{3}} \end{aligned}\]\)
Therefore, we have found the curl and divergence of the given vector field as follows:
\(\[\nabla \times \vec{F}=\left(-\frac{x}{y^{3}}\right) \vec{i}+\left(\frac{2 x}{z^{2}}-\frac{y^{2}}{z^{2}}\right) \vec{j}+\vec{0}\]\[\nabla \cdot \vec{F}=\frac{z^{3}+2 y^{3}-2 x^{2} y^{2}}{y^{2} z^{3}}\]\)
Hence, the required curl and divergence of the given vector field are as mentioned above.
to know more about vector field visit:
https://brainly.in/question/44187677
#SPJ11
The given vector field is
\($\mathbf{F}(x, y, z)=\frac{x}{y^{2}} \boldsymbol{i}+\frac{y^{2}}{z} j+\frac{x^{2}}{z^{2}} \boldsymbol{k}$\).
Let's calculate the curl and divergence of \($\mathbf{F}(x, y, z)$\).
Curl of \($\mathbf{F}(x, y, z)$\) is given as,
\($$\nabla \times \mathbf{F}(x, y, z)=\left(\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}\right) \boldsymbol{i}+\left(\frac{\partial R}{\partial x}-\frac{\partial P}{\partial z}\right) j+\left(\frac{\partial Q}{\partial z}-\frac{\partial R}{\partial y}\right) \boldsymbol{k}$$\)
Here \($P=\frac{x}{y^{2}}$\), \($Q=\frac{y^{2}}{z}$\) and\($R=\frac{x^{2}}{z^{2}}$\).
Hence,
\($$\frac{\partial P}{\partial y}=-\frac{2x}{y^{3}}, \quad \frac{\partial Q}{\partial x}=0, \quad \frac{\partial R}{\partial y}=0$$\)
\($$\frac{\partial P}{\partial z}=0, \quad \frac{\partial Q}{\partial z}=-\frac{y^{2}}{z^{2}}, \quad \frac{\partial R}{\partial x}=\frac{2x}{z^{2}}$$\)
Substituting these values in the curl of \($\mathbf{F}(x, y, z)$\), we get,
\($$\nabla \times \mathbf{F}(x, y, z)=\left(\frac{2x}{y^{3}}\right) \boldsymbol{i}+\left(\frac{2x}{z^{2}}\right) \boldsymbol{k}$$\)
Hence, the curl of \($\mathbf{F}(x, y, z)$\)is
\($\nabla \times \mathbf{F}(x, y, z)=\left(\frac{2x}{y^{3}}\right) \boldsymbol{i}+\left(\frac{2x}{z^{2}}\right) \boldsymbol{k}$\).
Divergence of \($\mathbf{F}(x, y, z)$\)is given as,
\($$\nabla \cdot \mathbf{F}(x, y, z)=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}$$\)
Hence, \($$\frac{\partial P}{\partial x}=\frac{1}{y^{2}}, \quad \frac{\partial Q}{\partial y}=\frac{2y}{z}, \quad \frac{\partial R}{\partial z}=-\frac{2x^{2}}{z^{3}}$$\)
Substituting these values in the divergence of \($\mathbf{F}(x, y, z)$\), we get,
\($$\nabla \cdot \mathbf{F}(x, y, z)=\frac{1}{y^{2}}+\frac{2y}{z}-\frac{2x^{2}}{z^{3}}$$\)
Hence, the divergence of \($\mathbf{F}(x, y, z)$\) is
\($\nabla \cdot \mathbf{F}(x, y, z)=\frac{1}{y^{2}}+\frac{2y}{z}-\frac{2x^{2}}{z^{3}}$\).
To know more about curl visit:
https://brainly.com/question/33160651
#SPJ11
In a recent survey, the proportion of adults who indicated mystery as their favorite type of book was 0.325. Two simulations will be conducted for the sampling distribution of a sample proportion from a population with a true proportion of 0.325. Simulation A will consist of 1,500 trials with a sample size of 100. Simulation B will consist of 2,000 trials with a sample size of 50. Which of the following describes the center and variability of simulation A and simulation B?
Answers
Option c) The centers will roughly be equal, and the variability of simulation A will be less than the variability of simulation B
According to the information given in the question,
A true proportion of 0.325 represents that the two simulations will be conducted for sampling proportions from a population
Simulation A -
Sample size - 100
Trials - 1500
Simulation B -
Sample size - 50
Trials - 2000
Now due to the relation of simulation A and simulation B, they are closely equal-
The total sample size of simulation A= 1500 x 100
= 150000
The total sample size of simulation B = 2000 x 50
= 100000
From the above calculations of simulations A and B, we can see that while comparing the,
Sample Size = Simulation A > Simulation B
Variability = Simulation B < Simulation B
Therefore, option c) The centers will roughly be equal, and the variability of simulation A will be less than the variability of simulation B is correct.
To learn more about Sampling Simulation questions on mathematics,
https://brainly.com/question/16359096
#SPJ4
In a recent survey, the proportion of adults who indicated mystery as their favorite type of book was 0.325. Two simulations will be conducted for the sampling distribution of a sample proportion from a population with a true proportion of 0.325. Simulation A will consist of 1,500 trials with a sample size of 100. Simulation B will consist of 2,000 trials with a sample size of 50. Which of the following describes the center and variability of simulation A and simulation B?
A) The centers will roughly be equal, and the variabilities will roughly be equal.
B) The centers will roughly be equal, and the variability of simulation A will be greater than the variability of simulation B.
C) The centers will roughly be equal, and the variability of simulation A will be less than the variability of simulation B.
D) The center of simulation A will be greater than the center of simulation B, and the variability of simulation A will roughly be equal to the variability of simulation B.
E) The center of simulation A will be less than the center of simulation B, and the variability of simulation A will be greater than the variability of simulation B.
the speed of a lazy river current is 5 mph. if a boat travels 20 miles downstream at the same time that it takes to travel 10 miles upstream, find the speed of the boat on still water.
Answers
The speed of boat in still water is 15 m per hour.
What is speed?
The speed of an object, also known as v in kinematics, is the size of the change in that object's position over time or the size of the change in that object's motion per unit of time, making it a scalar quantity. The instantaneous speed is indeed the upper limit of a average speed as that of the length of the interval approaches zero. The average speed of the object in a period of time is equal to the distance travelled by object divided by duration of the period. Velocity and speed are not the same thing.
The dimensions of speed are time divided by distance.
Given, speed of lazy river current = 5
distance covered = 20 miles downstream
and 10 miles upstream
Let x be the speed in still water
(x+5)T = 20
(X-5)T= 10
2(X-5) = (X+5)
X = 15
Therefore, speed of the boat in still water is 15 m per hour
To know more about speed, visit:
https://brainly.com/question/27870450
#SPJ4
rewrite the expression without using grouping symbols
13(19 - x)
A.) 13+19-13+x
B.)1319-13x
C.) 13 * 19 - 13x
D.) 13 *19 - x
Answers
Answer:
Step-by-step explanation:
the answer is c
after distributing 13 to the expression within the Parentheses we get the equation 13*19 - 13x which can then be further simplified to 247 - 13x
Mr. Browner has 7 keys. He has 1 key
for his home, 2 keys for his car, and
the rest are for drawers in his office.
If Mr.
Browner picks one of his keys
without looking, what is the probability
it is for his car?
Options: 1/7, 2/7, 3/7, 5/7, 6/7
Answers
Answer:
2/7
Step-by-step explanation:
there are 7 total possibilities for the keys he picks, and out of those possibilities, 2 of them are car keys. this means the probability that it is for his car is 2/7.
\(\huge\mathscr\color{gold}\colorbox{black}{ANSWER:}\)
\({\qquad\qquad\qquad}\)
You can choose Options: 2/7
\(__________________________________\)
\(\large\mathcal\color{gold}\colorbox{black}{STEP-BY-STEP\: EXPLANATION:}\)
\({\qquad\qquad\qquad}\)
Will i can choose 2/7 because 7 is probability keys he picks, and 2 keys he picks for looking a drawers in office to finding.
\(__________________________________\)
Hope it helps Correct me if I'm wrong\(__________________________________\)
\(\normalsize\color{brown}\boxed{☕TheQuestionner☕}\)
HELP PLS ILL MARK BRAINLIEST PLEASEEEEEEEEE
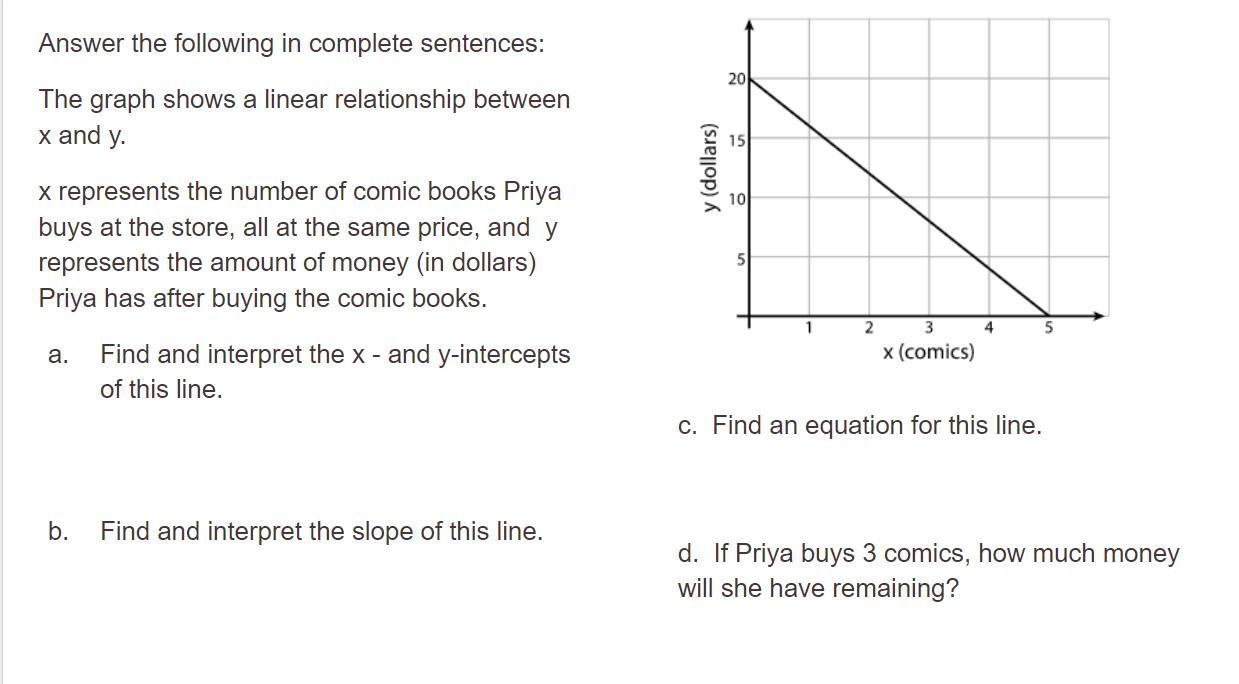
Answers
Answer: A
Step-by-step explanation: because I had that same test last year
4x + 3y = 6
3x + 5y = -1
Solve the simultaneous equations.
y=
z=

Answers
Answer:
x=3, y= -2
Step-by-step explanation:
Multiplying :
(4x+3y =6)*-3
(3x+5y =-1)*4
-12x -9y= -18
12x+20y= -4
Add the equations
20y-9y = -4-18
11y = -22
y= -22/11 = -2
3x +5* -2= -1
3x -10 = -1
3x = 10-1
x= 9/3 =3
a random sample of 150 people was taken. 98 of the people in the sample favored candidate a. we are interested in determining whether or not the proportion of the population in favor of candidate a is significantly more than 57%. [r] refer to exhibit 9-6a. at the 0.1 level of significance, what conclusion do you draw? group of answer choices
Answers
At the 0.1 level of significance, the conclusion we come up with is to reject the null hypothesis.
we are given that a random sample of 150 people was taken. 98 of the people in the sample favored the candidate, were it to determine whether or not the proportion of the population in favor of candidate a is significantly more than 57%.So we need to find the test statistic, which is 1.98 determined from the z score, here the rejection region is the number more than 1.28, and 1.98 is greater than 1.28, so it is better to simply reject the null hypothesis.
to know more about the null hypothesis refers to the link https://brainly.com/question/28920252?referrer=searchResults.
#SPJ4
how can i melt ice the fastest
1.)state an observation
2.)form a testable hypothesis
3.)explain how you would test it
4.)describe how you could analyze your results
5.)state your conclusion
Answers
Answer:
1. Ice melts under heat and temperatures above freezing point.
2. If I leave my ice underneath the sun, then it will melt.
3. I would test it by putting ice into a bowl and leave it outside for five minutes.
4. After five minutes, I would go outside and see what percentage of the ice has melted.
5. Ice melts underneath high temperatures and the higher the temperature, the faster the ice melts.
Step-by-step explanation:
Which pair of angles must be supplementary? 50 POINTS!!! 2 lines intersect to form right angles. Another line goes through the lines diagonally to form 6 angles. From top left, clockwise, the angles are 2 (90 degrees), 1, 6, 5 (90 degrees), 4, 3. Angle 1 and Angle 6 Angle 2 and Angle 5 Angle 5 and Angle 4 Angle 6 and Angle 2
Answers
Answer:
1,6
Step-by-step explanation:
i just did the test on edge
Answer:
angle 6,2
Step-by-step explanation:
supplementary angles means that the sum of all the angle eqaul 180 degrees, so 6,2 would equal 180 degrees
And i got it correct on e d gu n i t y 2020
if P1 is (3,-3) and the midpoint is (-2,1), what are the points of P2?
Answers
Step-by-step explanation:
Hey there!
The points P1(3,-3) and midpoint is (-2,1). Let (X,y) be the end point.
Note: Find through using midpoint formula.
midpoint = ( \frac{x1 + x2}{2} , \frac{y1 + y2}{2} )
Put all values.
(\frac{X+3}{2},\frac{-3+y}{2})
Since they are equal, equating with it's corresponding components.
\frac{3 + x}{2} = - 2
-2 = 3 + x
-4 -3= x
Therefore, X= -7.
Now,
\( \frac{ - 3 + y}{2} = 1\)
\( - 3 + y = 2\)
Therefore, y= 5
Therefore, the other end point is (3,5).
Hope it helps...
In isosceles triangle ABC, AB=AC.If B=55, calculate A
Answers
Answer: ∠A = 70°
because ABC is an isosceles triangle and AB = AC
=> ∠B = ∠C = 55°
=> ∠A = 180-(∠B + ∠C) = 180° - 55°.2 = 70°
Step-by-step explanation:
sorry i can't help :(
need help pls!!!!!!!!!!

Answers
Answer: 4 side faces and one base faces I believe im sorry times a 100 if its wrong
Step-by-step explanation:
Solve the following quadratic equation using the completing the square method.
x² - 10x + 4 = 0
Answers
Answer:
x is equal to 5 ± i√21
Step-by-step explanation:
x² -10x + 4 = 0
x²- 10x -25 = -21
(x - 5)² = -21
x - 5 = √(-21)
x = 5 ± √(-21)
x = 5 ± i√21
Can someone help me ASAP please

Answers
Answer:
Y=2x-3
Step-by-step explanation:
a) Let Y ~ Exp(β). Derive mY(t), the mgf of Y (your answer shall be an explicit function of β and t, and shall not contain any expectation or integration). Why is the mgf undefined for t ≥ 1/β ?
b) Let Y ∼ Poi(λ). Derive mY (t), the mgf of Y (your answer shall be an explicit function of β and t, and shall not contain any expectation or integration).
Answers
To derive this, we first use the definition of the Poisson distribution and write the expected value as an infinite sum. We then substitute the pmf of the Poisson distribution and simplify the sum using the Taylor series expansion of e^x. This gives us the mgf of Y as \(e^λ(e^t - 1).\)
a) The moment-generating function (mgf) of a random variable Y is defined as \(M(t) = E[e^(tY)]. For Y ~ Exp(β),\) we have:
\(M(t) = E[e^(tY)] = ∫₀^∞ e^(ty) βe^(-βy) dy = β/(β-t)\)
To derive this, we first use the definition of the exponential distribution and write the expected value as an integral from 0 to infinity. We then substitute the pdf of the exponential distribution and simplify the integral using the rule for the integral of e^(-ax) from 0 to infinity, which is a/(a+t). This gives us the mgf of Y as β/(β-t).
The mgf is undefined for t ≥ 1/β because the integral ∫₀^∞ e^(ty) βe^(-βy) dy diverges for these values of t, meaning that the mgf does not exist.
b) For Y ~ Poi(λ), the mgf is given by:
\(M(t) = E[e^(tY)] = ∑_{y=0}^∞ e^(ty) (λ^y / y!) e^(-λ) = e^λ(e^t - 1)\)
To derive this, we first use the definition of the Poisson distribution and write the expected value as an infinite sum. We then substitute the pmf of the Poisson distribution and simplify the sum using the Taylor series expansion of e^x. This gives us the mgf of Y as e^λ(e^t - 1).
Note that this mgf is defined for all values of t.
To know more about integration here
https://brainly.com/question/19815172
#SPJ4
replacement times for cd players are normally distributed with a mean of ten years and the variance of two. find the replacement time separating the bottom 30% to the top 70%.
Answers
The replacement time separating the bottom 30% to the top 70% of CD players is 9.27 to 10.73 years.
What is meant by normally distributed data?A normal distribution refers to a continuous probability distribution in statistics that is symmetric and bell-shaped. It is a statistical distribution that is ideal for data that are continuous and normally distributed in a population.
The central limit theorem states that any large number of independent random variables, each with its own distribution, have their sum distribution approach normality as the number of variables grows large enough.
The formula for z-score is given as:
z = (x - μ) / σ
where x is the random variable, μ is the mean, σ is the standard deviation, and z is the z-score.
Substituting the given values of the mean, standard deviation, and percentiles in the above formula, we get:
For the bottom 30%, the percentile rank is 0.3.
Hence, the z-score is given as:
z = invNorm(0.3) = -0.5244
Substituting the z-score formula we get:
-0.5244 = (x - 10) / √2
Rearranging the above formula we get:
x = -0.5244 * √2 + 10 = 9.27 years
For the top 70%, the percentile rank is 0.7.
Hence, the z-score is given as:
z = invNorm(0.7) = 0.5244
Substituting the z-score formula we get:
0.5244 = (x - 10) / √2
Rearranging the above formula we get:
x = 0.5244 * √2 + 10 = 10.73 years
Therefore, the replacement time separating the bottom 30% to the top 70% of CD players is 9.27 to 10.73 years.
Learn more about normal distribution at
https://brainly.com/question/3930800
#SPJ11
Suppose you scored 81,75,79, and 91 on your four exams in a mathematics course. Calculate the range and standard deviation of your exam scores. Round the mean to the nearest tenth to calculate the standard deviation. The range of the exam scores is (Simplify your answer.)
Answers
The range and standard deviation of your exam scores is 16 and 5.87, respectively.
The range is calculated by finding the difference between the highest and lowest values in a set of data. In this case, the highest score is 91 and the lowest score is 75. Subtracting 75 from 91, we get a range of 16.
The standard deviation measures the variability or spread of a set of data. To calculate the standard deviation, we first need to find the mean (average) of the exam scores.
To find the mean, add up all the scores and divide the sum by the total number of scores. In this case, the sum of the scores is 81 + 75 + 79 + 91 = 326. Since there are 4 scores, we divide 326 by 4 to get a mean of 81.5 (rounded to the nearest tenth).
Next, for each score, subtract the mean and square the result. Then, sum up all these squared differences.
For the score 81: (81 - 81.5)² = 0.25
For the score 75: (75 - 81.5)² = 42.25
For the score 79: (79 - 81.5)² = 6.25
For the score 91: (91 - 81.5)² = 89.25
Summing up these squared differences, we get 0.25 + 42.25 + 6.25 + 89.25 = 138.
To calculate the variance, divide this sum by the number of scores (4) to get 138/4 = 34.5.
Finally, to find the standard deviation, take the square root of the variance. The square root of 34.5 is approximately 5.87 (rounded to the nearest hundredth).
So, the range of the exam scores is 16 and the standard deviation is 5.87.
Learn more about standard deviation here: https://brainly.com/question/24298037
#SPJ11
It takes Camden 45 min to complete 1/5 of his art project. How many hours will it take home to finish the project if he works at the same rate.
Answers
my parents started a small farm after they retired. on their farm, they have chickens and pigs. in total, there are 40 animal legs among the chickens and the pigs, and there are 16 animal heads. how many chickens do my parents have?
Answers
Let's use "x" for the quantity of hens and "y" for the quantity of pigs.
A farm has 11 chickens, thus 2x + 4y = 40, x + y = 16.
What exactly does the term "farm" mean?a plot of land, sometimes along with a house and other structures, that is used for raising crops or rearing animals. A cow or mink farm is an example of a location where a particular kind of animal is raised in great numbers for sale.
How come it's called a farm?It was typical in the late Middle Ages to rent or lease land suitable for farming for a set monetary sum rather than a proportion of the crop. The amount that needed to be paid was referred to as ferme, or, in Modern English,farm.
To know more about Farm visit:
https://brainly.com/question/12586721
#SPJ4
Will mark brainliest if correct.

Answers
Answer:
b
Step-by-step explanation:
Answer:
i am pretty sure the answer is d
Step-by-step explanation:
let me know if this is wrong
YOU WILL GET 50 OR 100 POINTS TO THE FIRST PERSON TO ANWSER!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! Antonio circled 72, 78, 84, and 90 on a hundreds chart. If Antonio continues his pattern, what two numbers will be next in the pattern?
Answers
Answer:
96, 102Step-by-step explanation:
We can observe the numbers 72, 78, 84, 90 form an arithmetic sequence with common difference of 6.
It can be continued by adding 6 to the last number:
90 + 6 = 9696 + 6 = 10272,78,84,90..are in AP
a=72d=6\(\\ \rm\longmapsto a_5=72+4(6)=72+24=96\)
\(\\ \rm\longmapsto a_6=72+5(6)=72+30=102\)
If a varies inversely as square root of b, and a = 7 when b = 36, find a when b = 196.
Answers
Answer:
a = 3
Step-by-step explanation:
a = k/√b
First, we find k:
a = 7; b = 36
7 = k/√36
7 = k/6
k = 42
Now we write the equation of the relation:
a = 42/√b
b = 196
a = 42/√196
a = 42/14
a = 3
What is the slope of the line?

Answers
Answer:
The slope is 1/2
Step-by-step explanation:
I did rise over run
Two cards are drawn from the pack of 52 cards. Find the probability that both are diamonds or both are kings.
Answers
=========================================================
Work Shown:
There are 13 diamond cards. The probability of getting a diamond card is 13/52 = 1/4.
Assuming the first card is not replaced, the probability of getting another diamond card is 12/51. Note how I subtracted 1 from the numerator and denominator of 13/52 to get 12/51.
Multiply the two fractions to get
(1/4)*(12/51) = 12/204 = 1/17
The probability of getting two diamonds in a row is 1/17
We'll use this later, so let A = 1/17.
---------------------
There are 4 kings. The probability of pulling out a king is 4/52 = 1/13
The probability of pulling out another king is 3/51 = 1/17
The probability of pulling out two kings in a row is (1/13)*(1/17) = 1/221
Let B = 1/221
---------------------
Add the values of A and B
A+B = 1/17 + 1/221
A+B = 13/221 + 1/221
A+B = (13+1)/221
A+B = 14/221
A+B = 0.0633 which is approximate
That converts to 6.33% when you move the decimal point over 2 spots to the right.
We have that the probability that both are diamonds or both are kings.
P(D+K)=32\%
From the question we are told
Two cards are drawn from the pack of 52 cards. Find the probability that both are diamonds or both are kings.
Generally the equation for the both are diamonds or both are kings is mathematically given as
\(P(D+K)=\frac{d}{52}+ \frac{k}{52}\)
Therefore
\(P(D+K)=\frac{13}{52}+ \frac{4}{52}\\\\P(D+K)=0.32\)
P(D+K)=32\%
For more information on this visit
https://brainly.com/question/23366835
Which step is the same when constructing an inscribed square and an inscribed regular hexagon?
Answers
Answer:
Step-by-step explanation:
Connect every arc along the circle.
Construct a circle of any arbitrary radius.
Set the compass width to greater than half the diameter of the circle.
Set the compass width to the radius of the circle.
Aldrine is buying coffee for his coworkers. He orders small and large coffees. Small coffees
cost $3 and large coffees cost $5. He spent $30 and ordered eight cups of coffee in total.
Write a system of equations that represents the situation
How many of each coffee did he buy? How do you know?

Answers
Let small cups = S
Large cups = L
They bought a total of 8 cups, so S + L = 8
Rewrite as S = 8-L (1st equation)
Then you also have
$3S + $5L = $30 (2nd equation)
Replace the S in the second equation with the first equation:
$3(8-L) + $5L = $30
Simplify:
24 - 3L + 5L = 30
Combine like terms:
24+2L = 30
Subtract 24 from both sides:
2L = 6
Divide both sides by 2:
L = 3
They bought 3 large cups
Since they bought a total of 8 cups, that means they bought 5 small cups ( 8-3=5)
Large = 3 cups, Small = 5 cups