At a vacation resort, the afternoon activity is either hiking or horseback riding. The activity organizers track the participants by age and create this frequency table. which statement best summarizes interest in hiking by the age categories shown in the table?

Answers
1) Given that Relative Frequency, is a measure of frequency in percentage (roughly speaking) so we need to insert other data for that table
Age Group Relative Frequency
Under 50 | 50 and over Under 50 | 50 and over
Hiking 28 26 61% 67%
Horseback Riding 18 13 39% 33%
Total 46 39
We can find the percentage using proportions like that:
46 ---100%
28 x
x = 2800/46
39-------100
26----- y
y = 67%
39----100
13-----z
z= 1300/39 = 33%
2) Examining the options
We have as the correct answer, the last one:
"The relative frequency for participants age 50 or over who prefer hiking is 6 percentage points more than that of participants under age 50 who prefer hiking " ( 67% to 61%)
Related Questions
Evaluate the definite integral of sin^5(x)dx from 0 to pi/2.
Answers
Step-by-step explanation:
The definite integral of sin^5(x)dx from 0 to pi/2 can be evaluated using the method of substitution.
Let u = sin(x), then du = cos(x)dx
The integral becomes:
∫sin^5(x)dx = ∫u^5du from 0 to sin(π/2)
= (u^6)/6 evaluated at sin(π/2) and 0
= (sin^6(π/2))/6 - 0
= (1^6)/6
= 1/6
So, the definite integral of sin^5(x)dx from 0 to pi/2 is equal to 1/6.
Jude is arranging for a party to be held in the students' union. The use
of the hall will be free but security costs of £300 will have to be met.
The cost of the main band will be £2,500 and the supporting band will
cost £500. Tickets will be priced at £16 each. On arrival, every ticket
holder will be given a bottle of water, worth £1 per bottle. If Jude sells
400 tickets as he anticipates, what profit will he make?
19:08
Answers
The profit that Jude made during the party was £3700.
What is profit?Profit is the difference between revenue and cost. It is given by:
Profit = Revenue - Cost
From the question:
The total cost = 300 + 2500 + 500 + (1 * 400 people) = £3700
Revenue = 400 ticket * £16 = £6400
Profit = Revenue - Cost = £6400 - £3700
The profit that Jude made during the party was £3700.
Find out more on profit at: https://brainly.com/question/23103804
A doll sold for $228 in 1975 and was sold again in 1986 for $472. Assume that the growth in the value V of the collector's item was exponential.
a) Find the value k of the exponential growth rate. Assume V₁ = 228.
(Round to the nearest thousandth.)
Answers
The value k of the exponential growth rate will be 0.045.
Given that:
$228 in 1975
$472 in 1986
Let 'x' be the number of years and 'y' be the selling price. Then the equations are given as,
\(\rm 288 = P_o \times e^{k *1975} \ \ \ \ \ \ ...(1)\\\\\rm 472 = P_o \times e^{k *1986} \ \ \ \ \ \ ...(2)\)
From equations (1) and (2), then
\(e^{k(1986 - 1975)} = \dfrac{472}{288}\\\\e^{k(1986 - 1975)} = 1.63889\)
Take log on both sides, then
k x (11) = ln 1.63889
k = 0.494/11
k = 0.045
The value k of the exponential growth rate will be 0.045.
More about the exponent link is given below.
https://brainly.com/question/5497425
#SPJ1
select an expression that is equivalent to 2^4/8

Answers
Answer:
The answer is C
Step-by-step explanation:

c. 8√(2^4 )
given 2^(4/8) can be written as 2^(4×1/8)
eg: 2^(1/2) is √2 hence same rule we can apply here and since 2^(1/8) we can write as 8√2 and given 2^4
further knowledge: so if asked to expand more we can write it as 8√16 simplifying this further we get 2^(1/2) which is actually √2
for more on square roots: https://brainly.com/question/29286039
Tell whether each ordered pair is a solution of the equation: 2x - y = 4, ( 3, -2 )
Answers
The ordered pair (3, - 2) is not a solution to the equation 2x - y = 4
What is an ordered pair?An ordered pair is made up of the ordinate and the abscissa of the x coordinate, with two values given in parenthesis in a certain sequence.
Pair in Order = (x,y)
x is the abscissa, the distance measure of a point from the primary axis x
y is the ordinate, the distance measure of a point from the secondary axis y
Given, an equation 2x - y = 4 now if (3, - 2) is an ordered pair then putting the numerical value of x must satisfy the y value.
when x = 3,
2(3) - y = 4.
6 - y = 4.
- y = 4 - 6.
- y = - 2.
y = 2.
So, (3, - 2) is not a solution to an equation 2x - y = 4.
learn more about the ordered pair here :
https://brainly.com/question/28874341
#SPJ1
Find a vector function, r(t), that represents the curve of intersection of the two surfaces. The paraboloid z = 6x2 + y2 and the parabolic cylinder y = 5x2.
Answers
Answer:
\(\mathbf{r^{\to} (t) = ti^{\to} + 5t^2^{\to} j+(6t^2 + 25t^4) k ^{\to}}\)
Step-by-step explanation:
Given that:
The paraboloid surface z = 6x² + y² and the parabolic cylinder y = 5x²
Let assume that:
x = t
then from y = 5x², we have:
y = 5t²
Now replace y = 5t² and x = t into z = 6x² + y²
z = 6t² + (5t²)²
z = 6t² + 25t⁴
Hence, the curve of intersection is illustrated by the set of equations:
x = t, y = 5t², and z = 6t² + 25t⁴
As a vector equation:
\(\mathbf{r^{\to} (t) = ti^{\to} + 5t^2^{\to} j+(6t^2 + 25t^4) k ^{\to}}\)
11. cos theta = 3/4, in quadrant 1
Answers
Answer:
Step-by-step explanation:sin
(
t
h
e
t
a
)
=
√
7
4
cos
(
t
h
e
t
a
)
=
3
4
tan
(
t
h
e
t
a
)
=
√
7
3
cot
(
t
h
e
t
a
)
=
3
√
7
7
sec
(
t
h
e
t
a
)
=
4
3
csc
(
t
h
e
t
a
)
=
4
√
7
7
find the measure of minor arc RV

Answers
The measure of the minor arc m∡rv = 111°
What is the explanation for the above response?Recall that according to the principle of angle of intersecting secants, (a-b)/2 = c
Where a = ∡RV
b = ∡SU = 37°:
and c = ∠T (the angle between intersecting secants.
Thus, if (a-b)/2 = c, and b = c = 37 degrees, then we can substitute these values into the equation to get:
(a - 37) / 2 = 37
Multiplying both sides by 2 gives:
a - 37 = 74
Adding 37 to both sides gives:
a = 111
Therefore, a is equal to m∡rv = 111°.
Learn more about Minor Arcs:
https://brainly.com/question/20511450
#SPJ1
Show that 5x^2 + 2x - 3 < 0 can be written in the form | x + 1/5 | < 4/5
if possible with the explanation as well
Answers
Step-by-step explanation:
First let solve the inequality
\(5 {x}^{2} + 2x - 3 < 0\)
Factor by grouping
\(5 {x}^{2} + 5x - 3x - 3 < 0\)
\(5x(x + 1) - 3(x + 1)\)
So the factor are
\((5x - 3)(x + 1)\)
So the factor are
\(x = \frac{3}{5} \)
and
\(x = - 1\)
Solutions to a quadratic can be represented by a absolute value equation because remeber quadratics
creates 2 roots and/or double roots.
The inequality
\( |x - b| < c\)
works as
b is the midpoint between 2 roots. And c is the
\( |x + b| = c\)
We know that the midpoint between both roots is-1/5.
so
\( |x - ( - \frac{1}{5} )| < c\)
\( |x + \frac{1}{5} | < c\)
Let use roots 3/5
\( | \frac{3}{5} + \frac{1}{5} | = \frac{4}{5} \)
-1 works as well.
\( | - 1 + \frac{1}{5} | = | - \frac{4}{5} | = \frac{4}{5} \)
So the absolute value equation is
\( |x + \frac{1}{5} | < \frac{4}{5} \)
One angle of an isosceles triangle measures 76º. Which other angles could be in that
isosceles triangle? Choose all that apply.
Answers
Answer:
52 or 28
Step-by-step explanation:
An isosceles has 2 congruent angles.
There are 2 possibilities:
A) There are two 76-deg angles and one angle of a different measure.
76 + 76 + x = 180
x = 28
B) There are two congruent angles, and 76 is the non-congruent angle.
x + x + 76 = 180
2x = 104
x = 52
Answer: 52 or 28
A bag contains marbles of which 8 are blue; 5 are red; 3 are yellow, and 4 are orange. What is the probability of randomly drawing an orange marble, replacing it, and then drawing a blue marble?
Answers
A message is coded into the binary symbols 0 and 1 and the message is sent over a communication channel.
The probability a 0 is sent is 0.4 and the probability a 1 is sent is 0.6. The channel, however, has a random error that
changes a 1 to a 0 with probability 0.1 and changes a 0 to a 1 with probability 0.2. Show your work below.
a. What is the probability a 1 is received?
b. If a 1 is received, what is the probability a 0 was sent?
Answers
Answer:
A: the probability that a 1 is received is 0.56.
B: the probability that a 0 was sent given that a 1 is received is (2/25) * (1 - P(0 sent)).
Step-by-step explanation:
To solve this problem, we can use conditional probabilities and the concept of Bayes' theorem.
a. To find the probability that a 1 is received, we need to consider the two possibilities: either a 1 was sent and remained unchanged, or a 0 was sent and got flipped to a 1 by the random error.
Let's denote:
P(1 sent) = 0.6 (probability a 1 is sent)
P(0→1) = 0.2 (probability a 0 is flipped to 1)
P(1 received) = ?
P(1 received) = P(1 sent and unchanged) + P(0 sent and flipped to 1)
= P(1 sent) * (1 - P(0→1)) + P(0 sent) * P(0→1)
= 0.6 * (1 - 0.2) + 0.4 * 0.2
= 0.6 * 0.8 + 0.4 * 0.2
= 0.48 + 0.08
= 0.56
Therefore, the probability that a 1 is received is 0.56.
b. If a 1 is received, we want to find the probability that a 0 was sent. We can use Bayes' theorem to calculate this.
Let's denote:
P(0 sent) = ?
P(1 received) = 0.56
We know that P(0 sent) + P(1 sent) = 1 (since either a 0 or a 1 is sent).
Using Bayes' theorem:
P(0 sent | 1 received) = (P(1 received | 0 sent) * P(0 sent)) / P(1 received)
P(1 received | 0 sent) = P(0 sent and flipped to 1) = 0.4 * 0.2 = 0.08
P(0 sent | 1 received) = (0.08 * P(0 sent)) / 0.56
Since P(0 sent) + P(1 sent) = 1, we can substitute 1 - P(0 sent) for P(1 sent):
P(0 sent | 1 received) = (0.08 * (1 - P(0 sent))) / 0.56
Simplifying:
P(0 sent | 1 received) = 0.08 * (1 - P(0 sent)) / 0.56
= 0.08 * (1 - P(0 sent)) * (1 / 0.56)
= 0.08 * (1 - P(0 sent)) * (25/14)
= (2/25) * (1 - P(0 sent))
Therefore, the probability that a 0 was sent given that a 1 is received is (2/25) * (1 - P(0 sent)).
A message is coded into the binary symbols 0 and 1 and the message is sent over a communication channel. The probability a 0 is sent is 0.4 and the probability a 1 is sent is 0.6. The channel, however, has a random error that changes a 1 to a 0 with probability 0.2 and changes a 0 to a 1 with probability 0.1. (a) What is the probability a 0 is received? (b) If a 1 is received, what is the probability a 0 was sent?
2x+3y+1+3xi=x-2y+(3+y)i
Answers
Answer:
Step-by-step explanation:
I suppose the question is to solve the equation
\(2x+3y+1+3ix=x-2y+(3+y)*i\\\\2x+3y+1+3ix-x+2y-3i-iy=0\\\\x+5y+1+i(3x-y-3)=0\\\\\Longrightarrow\\\\\left\{\begin{array}{ccc|c|c|}x+5y&=&-1&-3&1\\3x-y&=&3&1&5\\\end{array}\right.\\\\\\\left\{\begin{array}{ccc}-16y&=&6\\16x&=&14\\\end{array}\right.\\\\\\\left\{\begin{array}{ccc}x&=&\dfrac{14}{16}\\\\y&=&\dfrac{-6}{16} \\\end{array}\right.\\\)
Please help! It’s worth 30 points!

Answers
Answer:
Step-by-step explanation:
Answer:
0.430
Step-by-step explanation:
thank you so much i really appreciate
For which value of a does lim g(x) not exist?
x-a
Answers
Answer:
X value de correct answer
Based on the graph of the given limit of a function, the value for which \(\lim_{x \to a} g(x)\) doesn't exist is equal to -3.
What is a limit?A limit can be defined as a numerical value which a function approaches (output) as the input value approaches other values. In Mathematics, limits are typically used to determine the following:
IntegralsDerivativesContinuityFor the right-hand limit, we have:
\(\lim_{x \to -3^{+}}[ -3 + 1] = -2\)
For the right-hand limit, we have:
\(\lim_{x \to -3^{-}} [-3 - 1] = -4\)
By critically observing the graph of the given limit of a function, we can logically deduce that -3 is the value for which \(\lim_{x \to a} g(x)\) doesn't exist because the right-hand limit and left-hand limit are not the same (different).
Read more on limit here: https://brainly.com/question/23343679
#SPJ6

While viewing a herd of cattle on a ranch, Herbert estimated that there were 750 cattle in the herd. The actual number of cattle in the herd was 600.
What was the percent of error, rounded to the nearest percent?
15%
20%
25%
30%
Answers
The solution is, the percent of error, rounded to the nearest percent is 25%.
What is percentage?A percentage is a number or ratio that can be expressed as a fraction of 100. A percentage is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign, "%", although the abbreviations "pct.", "pct" and sometimes "pc" are also used. A percentage is a dimensionless number; it has no unit of measurement.
here, we have,
given that,
While viewing a herd of cattle on a ranch, Herbert estimated that there were 750 cattle in the herd.
The actual number of cattle in the herd was 600.
now, we have to find the percent of error, rounded to the nearest percent.
so, we get,
Herbert estimated that there were 750 cattle in the herd.
The actual number of cattle in the herd was 600.
so, error = 750 - 600
= 150
so, we get,
the percent of error = 150 * 100 / 600
= 25%
Hence, The solution is, the percent of error, rounded to the nearest percent is 25%.
To learn more on percentage click:
brainly.com/question/13450942
#SPJ2
Andres works 20 hours per week at a part-time job. His original pay rate was $10.00 per hour, but he recently received a pay raise of x dollars per hour. His new total weekly pay, y, is represented by the equation y=20(10+x).
If Andres earned $210 last week, what was the amount of Andres' raise per hour?
Answers
Answer:
X = .5
Step-by-step explanation:
10 × 20 = 200
10.5 × 20 = 210
Explanation:
Y = 210
210 = 20(10+X)
divide both sides by 20
10.5 = 10+X
subtract 10 from both sides
.5 = X
X = .5
Can someone help please? Picture is already attached. If its wrong please correct it. This isn’t mine by the way, I’m posting it for someone else to double check if it’s right

Answers
Answer:
You've got it right
Step-by-step explanation:
If you want to get stellar communication on the question then maybe include a number line to visually represent why, but otherwise you have the answer right.
Can some one tell me the answer

Answers
Answer:
x = 13°
Step-by-step explanation:
The total must be 180°.
105° + 62° = 167°
180° - 167°
13°
Answer:
the answer is 13
Step-by-step explanation:
half of 360 is 180 (it has to be this number in the end)
105+62-180=-13
to check: 105+62+13=180
One fruit punch has 10% juice and another has 50%. How much of the 10% should be mixed with 30 gal of the 50% to create punch that is 25% juice
Answers
Answer:
We combine x ounces of 100% juice
with 40-x of 10% juice
to get 40 ounces of 55% juice
x + 0.1(40-x) = .55(40)
x + 4 - 0.1x = 22
0.9x + 4 = 22
.09x = 18
x = 20 ounces of 100% juice
40-x = 20 ounces of 10% juice
We combine 20 ounces of each.
Step-by-step explanation:
1. A store manager marked up the price of a $12 clock by 20%. What is the new price of the clock?
2. On a math quiz, Kyra answered 7 of 10 questions correctly. Express her quiz score as a percent.
3. 96 students are enrolled in the Dance Program at Castillero. Of those students, 54 are eighth-graders. The remaining students are 6th or 7th graders. What percentage of the students are not eighth graders?
Answers
Answer:
1) new price of the clock is $14.4
2) Kyra scored 70% marks
3) 43.75% students are not eighth graders
Step-by-step explanation:
1. A store manager marked up the price of a $12 clock by 20%. What is the new price of the clock?
Price of Clock = $12
Mark up = 20%
We need to find new price of clock.
The price of clock can be found by finding 20% of 12 and then adding that amount in original price.
So, finding 20% of 12
\(20\% of 12 \\=\frac{20}{100}\times 12\\=2.4\)
So 20% of 12 is 2.4
Now finding new price:
New Price = Actual Price + Mark up
New Price = 12 + 2.4
New Price = 14.4
So, new price of the clock is $14.4
2. On a math quiz, Kyra answered 7 of 10 questions correctly. Express her quiz score as a percent.
Total questions = 10
Correct answers = 7
We need to express her quiz score as percent
It can be found using formula: \(Percent Score = \frac{Obtained\:Marks}{Total\:Marks}\times 100\%\\\)
Putting values and finding percentage
\(Percentage = \frac{Obtained\:Marks}{Total\:Marks}\times 100\%\\\\Percentage = \frac{7}{10}\times 100\%\\Percentage = 70\%\)
So, Kyra scored 70% marks
3. 96 students are enrolled in the Dance Program at Castillero. Of those students, 54 are eighth-graders. The remaining students are 6th or 7th graders. What percentage of the students are not eighth graders?
Total Students = 96
Number of eighth-graders students = 54
Remaining students = 96 - 54 = 42
So, 42 students are 6th or 7th graders
We need to find percentage of the students are not eighth graders.
\(\frac{42}{96}\times 100\%\\=43.75\%\)
So, 43.75% students are not eighth graders
How long does it take for an investment of $6,400 to increase to $14,000 if
it is invested at 5% per year compounded continuously? Round to the
nearest tenth of a year.
Answers
An investment of $6,400 to increase to $14,000 if it is invested at 5% per year compounded continuously is ≈15.6
Define compound interest?
Compound interest is the interest imposed on a loan or deposit amount. It is the most commonly used concept in our daily existence. The compound interest for an amount depends on both Principal and interest gained over periods.Given that :
P = $ 6,400
Q = $ 14,000
r = 5%
Let P be the initial investment
r be the rate of interest
t be the time
Q be the increase amount
Q = P \(e^{rt} }\)
14,000 = 6,400 (\(e^{0.05t}\))
\(e^{0.05t}\) = \(\frac{14000}{6400}\)
\(e^{0.05t}\) = 2.187
Taking log on both sides , we get
0.05t = ln (2.187)
0.05t = 0.78
t = \(\frac{0.78}{0.05}\)
t ≈ 15.6
An investment of $6,400 to increase to $14,000 if it is invested at 5% per year compounded continuously is ≈ 15.6
To learn more about compound interest check the given link
https://brainly.com/question/20406888
#SPJ1
HELPPPP?
find the concentration of sugar in the tank after 10 minutes.

Answers
Answer:
C(t) = 6/55
Step-by-step explanation:
Given:
t = 10
Work:
\(C(t)= \frac{4 +2t}{120+10t} \\\\C(t)= \frac{4 +2(10)}{120+10(10)}\\\\C(t)= \frac{4 +20}{120+100}\\\\C(t)= \frac{24}{220}\\\\C(t)=\frac{6}{55}\)
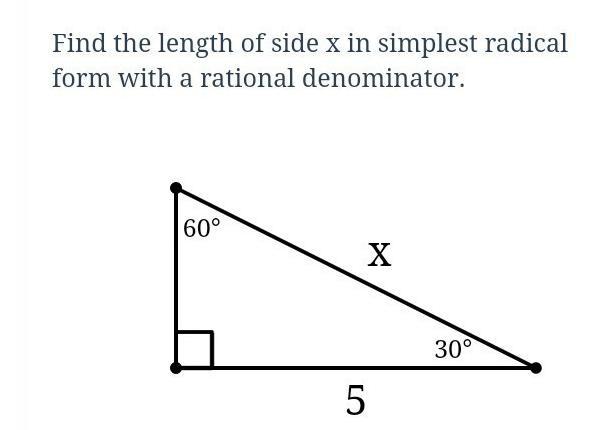
Find the length of side X in simple radical form with a rational denominator
Answers
The length of side X in simple radical form with a rational denominator is 25/√3.
What is a 30-60-90 triangle?In Mathematics and Geometry, a 30-60-90 triangle is also referred to as a special right-angled triangle and it can be defined as a type of right-angled triangle whose angles are in the ratio 1:2:3 and the side lengths are in the ratio 1:√3:2.
This ultimately implies that, the length of the hypotenuse of a 30-60-90 triangle is double (twice) the length of the shorter leg (adjacent side), and the length of the longer leg (opposite side) of a 30-60-90 triangle is √3 times the length of the shorter leg (adjacent side):
Adjacent side = 5/√3
Hypotenuse, x = 5 × 5/√3
Hypotenuse, x = 25/√3.
Read more on 30-60-90 triangle here: brainly.com/question/30283450
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.
Mr. Clark is contemplating which chauffeured car service to take to the airport. The first costs $28 up front and $1 per kilometer. The second costs $3 plus $2 per kilometer. For a certain driving distance, the two companies charge the same total fare. What is the total fare? What is the distance?

Answers
Answer:
The total fare is $53, and the distance is 25
Step-by-step explanation:
The equation we can use for the first car would be:
28 + (1×k) = fare (f)
The equation we can use for the second car would be:
3 + (2×k) = f
If we were to plug in 20 into the equations, it would look like this:
28 + (1×20) = 48 (first car)
3 + (2×20) = 43 (second car)
As you can tell, the prices aren't matched up just yet.
Let's plug 25 into the equations.
28 + (1×25) = 53
3 + (2×25) = 53
The number of kilometers traveled is 25, and the price is $53
Of the registered voters in the city of Bella Vista, 45% cast votes on a proposed school budget. Of those who voted, 68% voted to pass the school budget. What percent of registered voters in Bella Vista voted to pass the school budget?
Algebra
Answers
30.6% of registered voters in Bella Vista voted to pass the school budget.
What is successive percentage change?When more than one successive changes are applied to a quantity the total percentage change is called successive percentage change.
Given,
Percentage of registered voters casting vote = 45%
Of those who voted, percentage of voters who voted to pass the school budget = 68%.
Let, total registered voters = x .
Number of registered voters casting vote = 45% of x
= 45x/100
Total number of registered voters in Bella Vista who voted to pass the school budget = 68% of number of registered voters casting vote
= (68/100) × (45x/100)
Percentage of registered voters in Bella Vista who voted to pass the school budget = {(68/100) × (45x/100)} / x
= 30.6%
Hence, 30.6% of registered voters in Bella Vista voted to pass the school budget.
To learn more about percentage visit:
https://brainly.com/question/29306119
SPJ1
How to explain the question?
\(y = 2( { \frac{5}{4} )}^{2} - 5( \frac{5}{4} ) - 3\)
Answers
Answer:
\(32\)
\(i \: hope \: it \: helps \: mate \\ enjoy \: your \: day \\ \gamma captainpower\)
Which values of k are solutions to the inequality?
k>12
Select each correct answer.
k = 11.9
k = 12.1
k = 13.0
k = 19.9
k = 10.2

Answers
Answer:
B: k = 12.1
C: k = 13.0
D: k = 19.9 ARE THE CORRECT ANSWERS
Step-by-step explanation:
Answer:B: k = 12.1
Step-by-step explanation:
Convert 475 milliliter to liters.
Answers
0.475
1000 milliliters is equal to 1 liter
Answer: 0.475 Liters
Step-by-step explanation: So, we know one liter is exactly 1,000 milliliters...therefore this would have to be a decimal.
Therefore, 475 milliliters to liters would be 0.475 liters.
Brainliest
Sara and three of her friends used an Internet mapping application to map the location of each of their houses. Sara’s house is located at , Nate’s house is located at , Michelle’s house is located at , and Joshua’s house is located at .
(a) Plot the three points representing Sara’s, Nate’s, and Michelle’s houses.
(b) The friends discover that the four houses are the vertices of a rectangle. What are the coordinates of Joshua’s house? On the same grid, plot a point to represent Joshua’s house. Explain your answer.
Answer: