Area In Exercises 1-4, use finite approximations to estimate the area under the graph of the function using a. a lower sum with two rectangles of equal width. b. a lower sum with four rectangles of equal width. c. an upper sum with two rectangles of equal width. d. an upper sum with four rectangles of equal width.
Answers
a. Lower sum with two rectangles of equal width: Estimate the area under the graph using the sum of the areas of two rectangles, where each rectangle has a height equal to the minimum value of the function within its subinterval.
b. Lower sum with four rectangles of equal width: Estimate the area under the graph using the sum of the areas of four rectangles, where each rectangle has a height equal to the minimum value of the function within its subinterval.
c. Upper sum with two rectangles of equal width: Estimate the area under the graph using the sum of the areas of two rectangles, where each rectangle has a height equal to the maximum value of the function within its subinterval.
d. Upper sum with four rectangles of equal width: Estimate the area under the graph using the sum of the areas of four rectangles, where each rectangle has a height equal to the maximum value of the function within its subinterval.
To estimate the area under the graph of a function using finite approximations with different numbers of rectangles and equal widths, we can use the concepts of lower sums and upper sums.
a. Lower sum with two rectangles of equal width:
Divide the interval over which you want to estimate the area into two equal subintervals.
Approximate the area under the curve in each subinterval by a rectangle with height equal to the minimum value of the function within the subinterval.
Sum up the areas of the two rectangles to obtain the estimate of the area.
b. Lower sum with four rectangles of equal width:
Divide the interval into four equal subintervals.
Approximate the area under the curve in each subinterval by a rectangle with height equal to the minimum value of the function within the subinterval.
Sum up the areas of the four rectangles to obtain the estimate of the area.
c. Upper sum with two rectangles of equal width:
Divide the interval into two equal subintervals.
Approximate the area under the curve in each subinterval by a rectangle with height equal to the maximum value of the function within the subinterval.
Sum up the areas of the two rectangles to obtain the estimate of the area.
d. Upper sum with four rectangles of equal width:
Divide the interval into four equal subintervals.
Approximate the area under the curve in each subinterval by a rectangle with height equal to the maximum value of the function within the subinterval.
Sum up the areas of the four rectangles to obtain the estimate of the area.
To know more about minimum value,
https://brainly.com/question/25305847
#SPJ11
Related Questions
I need help, it is from my ACT prep guide I will add a picture with the answer options for the blank spaces


Answers
Given the equation below
\((y+5)^2=12(x+3)\)Step 1: Write out the standard form of the equation of a parabola
The standard form is
\(undefined\)I can't now the answer for this question. The question is, select all the number that are 10 times as much as 72. 67 or 1/10 of 72. 67
Answers
The only number that is 10 times as much as 72 is 720.
To find the numbers that are 10 times as much as 72 or 1/10 of 72, we can perform the following calculations:
10 times 72 = 720
1/10 of 72 = 7.2
So, the numbers that are 10 times as much as 72 are 720.
The number 67 is not 10 times as much as 72 or 1/10 of 72. Therefore, it is not one of the numbers we are looking for.
On the other hand, 1/10 of 72 is 7.2, which is not one of the numbers we are looking for either.
Therefore, the only number that is 10 times as much as 72 is 720.
To know more about number, visit: brainly.com/question/17429689
#SPJ4
complete question
Select all the numbers that are 10 times as much as 72, 67, or 1/10 of 72.
- 67
-46
-720
-480
Answer this question and show me how to check it

Answers
In order to rewrite these values in the standard form, let's calculate the product with the power of 10 from each number.
For the length, we have:
\(\begin{gathered} 8\cdot10^4 \\ =8\cdot10000 \\ =80000\text{ meters} \end{gathered}\)For the thickness, we have:
\(\begin{gathered} 5\cdot10^{-6} \\ =5\cdot0.000001 \\ =0.000005\text{ meters} \end{gathered}\)What are the correct trigonometric ratios that could be used to determine the length of ln? check all that apply. sin(20°) = startfraction l n over 8 endfraction cos(70°) = startfraction 8 over l n endfraction tan(70°) = startfraction l n over m n endfraction sin(20°) = startfraction 8 over l n endfraction cos(70°) = startfraction l n over 8 endfraction
Answers
The correct answer is option E which is Cos ( 70 ) = \(\dfrac{LN}{8}\).
The complete question is attached with the answer below:-
What is trigonometry?The branch of mathematics sets up a relationship between the sides and the angles of the right-angle triangle is termed trigonometry.
As we can see from the figure that ∠L = 70 and ∠M = 20 We can see that the length LN will be calculated as:-
Cos 70 = Base / Hypotenuse
So for an angle of 70, the base is LN and the hypotenuse is equal to 8 units.
Cos 70 = LN = 8
Therefore the correct answer is option E which is Cos ( 70 ) = \(\dfrac{LN}{8}\).
To know more about Trigonometry follow
https://brainly.com/question/24349828
#SPJ1

Answer:
A & E
Step-by-step explanation:
Jus took it on edge
Please help me. I'm confused.

Answers
Answer:
u is 4 and v is 18
Answer:
v = 18 ; u = 4
Step-by-step explanation:
In a parallelogram , the diagonals bisect each other . So,
v/3 = 6 ................ eqn.1
and
2u + 2 = 5u - 10 ................. eqn.2
From eqn.1,
v/3 = 6
=> v = 6×3 = 18
From eqn.2,
2u + 2 = 5u - 10
=> 5u - 2u = 10 + 2
=> 3u = 12
=> u = 4
5.86
What place value
position is the 5
in?
Answers
Answer:
if I am sure it is in 100 place.
Find the mean for the data set. 6, 14, 7, 4, 12, 8, 13, 4, 18, 14
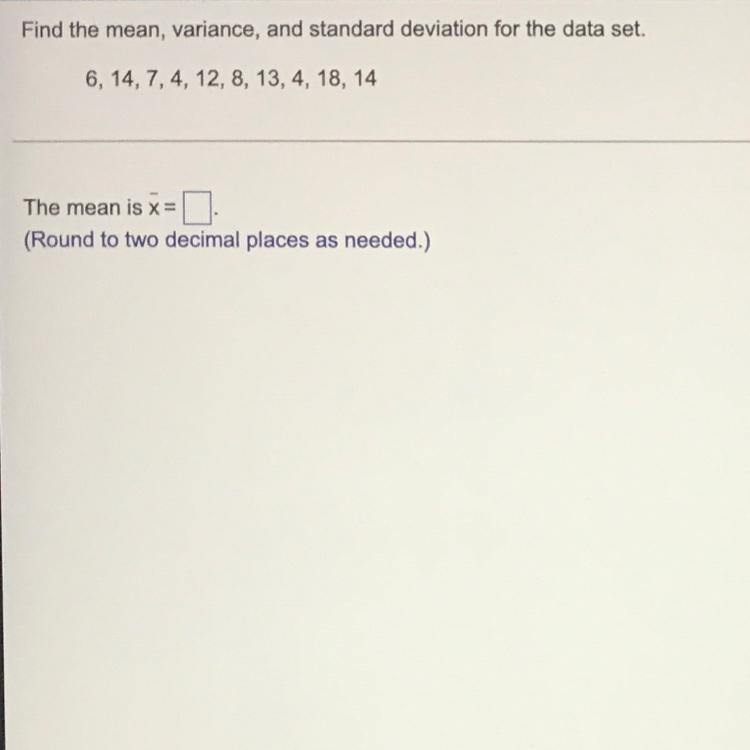

Answers
Answer:
Concept:
Mean is just another name for average. To find the mean of a data set, add all the values together and divide by the number of values in the set. The result is your mean!
The values are given below as
\(6,14,7,4,12,8,13,4,18,14\)The image below shows how to calculate the mean
By substituting values, we will have
\(\begin{gathered} \bar{x}=\frac{\sum ^{}_{n\mathop=0}x}{n} \\ n=10 \end{gathered}\)\(\begin{gathered} \bar{x}=\frac{6+14+7+4+12+8+13+4+18+14}{10} \\ \bar{x}=\frac{100}{10} \\ \bar{x}=10 \end{gathered}\)Hence,
The mean = 10
To calculate the variance, we will use the formula below
\(^{}\sigma^2=\frac{\sum ^{\infty}_{n\mathop=0}(x-\bar{x})^2}{n}\)\(\begin{gathered} \sigma^2=\frac{\sum ^{\infty}_{n\mathop{=}0}(x-\bar{x})^2}{n} \\ (x-\bar{x})^2=(6-10)^2+(14-10)^2+(7-10)^2+(4-10)^2+(12-10)^2+(8-10)^2+(13-10)^2+(4-10)^2+(18-10)^2+(14-10)^2 \\ (x-\bar{x})^2=16+16+9+36+4+4+9+36+64+16 \\ (x-\bar{x})^2=210 \end{gathered}\)\(\begin{gathered} \sigma^2=\frac{\sum ^{\infty}_{n\mathop{=}0}(x-\bar{x})^2}{n} \\ \sigma^2=\frac{210}{10} \\ \sigma^2=\frac{210}{10} \\ \sigma^2=21 \end{gathered}\)Hence
The variance = 21
To calculate the standard deviation,
\(\begin{gathered} \sigma=\sqrt[]{variance} \\ \sigma=\sqrt[]{21} \\ \sigma=4.58 \end{gathered}\)Hence,
The standard deviation is = 4.58

A submarine begins at -212 feet below sea level. If
the submarine plans to descend at 15 feet per minutes,
how long will it take the submarine to reach a depth of
-287 feet?
A. 75 minutes C. 7 minutes
B. 8 minutes D. 5 minutes
Answers
Answer:
Step-by-step explanation:
Ending depth = -287
Starting depth= -212
Difference = -75 feet
The submarine plans on dropping 15 feet a minute.
Time = displacement / time = -75/-15 = 5 minutes.
Answer: D
The graph shows the number of customers at a car wash for various outdoor temperatures.
Answers
The complete statement is -
The given graph is a scatter plot that uses the points to display the relationship between the number of customers and the temperature.
What is scatter plot?A scatter plot is a type of plot or mathematical diagram using Cartesian coordinates to display values for typically two variables for a set of data. If the points are coded, one additional variable can be displayed
Given is a scatter plot as shown in the image attached.
The given graph is a scatter plot that uses the points to display the relationship between the number of customers and the temperature.
Therefore, the complete statement is -
The given graph is a scatter plot that uses the points to display the relationship between the number of customers and the temperature.
To solve more questions on scatter plot, visit the link-
brainly.com/question/30098550
#SPJ1
A man sets out to travel from A to C via B. From A he travels a distance of 8km on a bearing N30degreesE to B. From B he travels further 6km due east. Calculate how far is north of A, east of A
Answers
The displacement of the man from Noth east of A from C is 12.2 km.
What is the displacement of the man?
The displacement of the man is the distance between his initial position at A and final position at C.
The angle formed at position B is calculated as follows;
θ = 30⁰ + 90⁰
θ = 120⁰
The displacement of the man is calculated by applying cosine rule as follows;
d² = 8² + 6² - 2(8 x 6) cos (120)
d² = 148
d = √148
d = 12.2 km
Learn more about displacement of vectors here: https://brainly.com/question/13416288
#SPJ1
What is the exact volume of the cylinder? A.) 54pi in3
B.) 108pi in3
C.) 162pi in3
D.) 324pi in3
PLEASE ANSWER FAST

Answers
Answer:
Choice D
Step-by-step explanation:
You use the formula V=pi(radius^2)(h). Once you take the pi out and plug in the numbers, you should get V= 6^2(9). You get 324 with the pi added on after it.
Answer:
B
Step-by-step explanation:
Just had this on a test!
Good luck!
Please mark brainliest!
Have an amazing day!
What’s the value for y?

Answers
Y=6-2
Y=4
The value of y is 4.
Consider the general problem: -(ku')' + cu' + bu = f, 0 Suppose we discretize by the finite element method with 4 elements. On the first and last elements, use linear shape functions, and on the middle two elements, use quadratic shape functions. Sketch the resulting basis functions. What is the structure of the stiffness matrix K (ignoring boundary conditions); that is indicate which entries in K are nonzero.
Answers
We need to consider the general problem: \[-(ku')' + cu' + bu = f\]If we discretize by the finite element method with four elements.
On the first and last elements, we use linear shape functions, and on the middle two elements, we use quadratic shape functions. The resulting basis functions are given by:The basis functions ϕ1 and ϕ4 are linear while ϕ2 and ϕ3 are quadratic in nature. These basis functions are such that they follow the property of linearity and quadratic nature on each of the elements.
For the structure of the stiffness matrix K, we need to consider the discrete problem given by \[KU=F\]where U is the vector of nodal values of u, K is the stiffness matrix and F is the load vector. Considering the above equation and assuming constant values of k and c on each of the element we can write\[k_{1}\begin{bmatrix}1 & -1\\-1 & 1\end{bmatrix}+k_{2}\begin{bmatrix}2 & -2 & 1\\-2 & 4 & -2\\1 & -2 & 2\end{bmatrix}+k_{3}\begin{bmatrix}2 & -1\\-1 & 1\end{bmatrix}\]Here, the subscripts denote the element number. As we can observe, the resulting stiffness matrix K is symmetric and has a banded structure.
The element [1 1] and [2 2] are common to two elements while all the other elements are present on a single element only. Hence, we have four elements with five degrees of freedom. Thus, the stiffness matrix will be a 5 x 5 matrix and the structure of K is as follows:
$$\begin{bmatrix}k_{1}+2k_{2}& -k_{2}& & &\\-k_{2}&k_{2}+2k_{3} & -k_{3} & & \\ & -k_{3} & k_{1}+2k_{2}&-k_{2}& \\ & &-k_{2}& k_{2}+2k_{3}&-k_{3}\\ & & & -k_{3} & k_{3}+k_{2}\end{bmatrix}$$Conclusion:In this question, we considered the general problem given by -(ku')' + cu' + bu = f. We discretized it by the finite element method with four elements. On the first and last elements, we used linear shape functions, and on the middle two elements, we used quadratic shape functions. We sketched the resulting basis functions. The structure of the stiffness matrix K was then determined by ignoring boundary conditions. We observed that it is symmetric and has a banded structure.
To know more about general problem visit
https://brainly.com/question/24486535
#SPJ11
Gracie has six dollars to buy a gallon of milk and some apples. The gallon of milk cost $3.59 and the apples cost $.60 each. Which any inequality could she use to find out how many apples she can buy?
Answers
Answer: 4
Step-by-step explanation:
Let the number of gallon milk cartons be M and the number of apples be N. The total cost would be 3.59M + 0.60N <= 6.00. If M = 1, then
3.59 + 0.60N <= 6.00
0.60N <= 2.41
N <= 4 [2.40, with 0.01 left over]
Scott has a blueprint of the new deck he is building with dimensions 7.5 inches by 4.5 inches. the actual deck will have dimensions 20 feet by 12 feet. what is the scale?
Answers
The scale factor of the blueprint of the deck is 1.5 inches = 4 feet
What is scale factor?A scale factor is defined as the ratio between the scale of a given original object and a new object, which is its representation but of a different size.
Given that, Scott has a blueprint of the new deck he is building with dimensions 7.5 inches by 4.5 inches. The actual deck will have dimensions 20 feet by 12 feet.
We need to find the scale factor,
7.5 / 20 = 1.5 / 4
Therefore,
There are 1.5 inches in 4 feet
Hence, the scale factor of the blueprint of the deck is 1.5 inches = 4 feet
Learn more about scale factors, click:
https://brainly.com/question/30215119
Answer:
hi
Step-by-step explanation:
guvuvugjdhddiebeidgddb
radius= 2 cm Side=5cm
Answers
Step-by-step explanation:
Radius (h) = 2cm
side (p) =5 cm
base (b) =?
So now
b^2 = h^2 - p ^2
b^2 = 2^2 - 5^2
b^2 = 4 - 25
b^2 = 21
b =√-21
Hope it helped you
please mark me the brainliest
Callie brushes her teeth three times each day. She leaves the water running. Is it reasonable to say that she uses 2 cups of water in one day? Explain
Answers
Answer: She uses more than 2 cups of water per day.
Step-by-step explanation:
It takes 2 minutes to brush your teeth and if you times that by 3 you get 6 so she spends 6 minuntes per day brushing her teeth and water runs fast. so if your leaving the water on for 6 mintues your filling up much more than 2 cups
Part A: In your own words, describe the relationship between the temperature of the city and the number of ice cream cones sold. (5 points)
Part B: Describe how you can make the line of best fit. Write the approximate slope and y-intercept of the line of best fit. Show your work, including the points that you use to calculate slope and y-intercept. (5 points)
Answers
Part A: The amount of ice cream increases as the temperature increases. Part B: the slope is 2 and the y-intercept will be 5.
What is the slope of a line which passes through points ( p,q) and (x,y)?Its slope would be:
\(m = \dfrac{y-q}{x-p}\)
Part A: The relationship between the temperature of the city and the number of ice cream cones sold.
From the graph, the dots on the graph increase in the up-right direction.
Thus, The amount of ice cream increases as the temperature increases.
Part B: The line of best fit
First, if we draw a line through the points
we select any 2 points on the line:
( p,q) and (x,y) as (15, 35) and (0, 5).
The slope (m) is:
\(m = \dfrac{y-q}{x-p}\)
\(m = \dfrac{5 - 35}{0-15}\\\\m = 2\)
So, the line of best fit is:
y = mx + c
y = 2(x - 0) + 5
y = 2x + 5
The y-intercept will be when x = 0
y = 2x + 5
y = 0 + 5
y = 5
Thus, the slope is 2 and the y-intercept will be 5.
Learn more about slopes here:
https://brainly.com/question/2503591
#SPJ1

Round 6.235 to the nearest hundredth.
Answers
Answer: 6.24
Step-by-step explanation:
To round 6.235 to the nearest hundredth means to round the numbers so you only have two digits in the fractional part (numbers after the decimal)
The last digit in the fractional part of 6.235 is 5 or more and less than 9, so add 1 to the second digit of the fractional part and remove the third digit.
Therefore, the answer is 6.24
Find the midpoint of segment CD, given that C is (-4, 7) and D is (0, -3).
Answers
change in y = -10
halfway between
x 2
y -5
so -2,2
Answer:
(-2, 2)
Step-by-step explanation:
\(Midpoint \: of \: segment \: CD \\\\ = \bigg( \frac{ - 4 + 0 }{2}, \: \: \frac{7 + ( - 3)}{2} \bigg) \\ \\ = \bigg( \frac{ - 4 }{2}, \: \: \frac{7 - 3}{2} \bigg) \\ \\ = \bigg( \frac{ - 4 }{2}, \: \: \frac{4}{2} \bigg) \\ \\ = ( - 2, \: \: 2)\)
use the ratio test to determine whether the series is convergent or divergent. [infinity] n 7n n = 1 identify an.
Answers
To determine whether the series ∑(n=1 to infinity) 7n/n is convergent or divergent, we can apply the ratio test. The ratio test helps us determine the convergence or divergence of a series by examining the limit of the ratio of consecutive terms.
In this case, let's calculate the ratio of consecutive terms using the formula for the ratio test:
lim(n→∞) |(7(n+1)/(n+1))/((7n/n)|
Simplifying the expression, we get:
lim(n→∞) |7(n+1)/n|
As n approaches infinity, the limit evaluates to:
lim(n→∞) |7(n+1)/n| = 7
Since the limit is a finite positive value (7), which is less than 1, the ratio test tells us that the series is convergent.
However, you mentioned identifying an (term) in the series, and it seems there may be an incomplete part of the question. Please provide additional information or clarification about identifying an term in the series so that I can provide a more specific answer.
To learn more about click here: brainly.com/question/12211820
#SPJ11
what does the word "solution" mean has to be in your own words please help
Answers
Answer:
an answer to a problem
Step-by-step explanation:
Which value for the constant d makes x = -2 an extraneous solution in the following equation?

Answers
The value for the constant d = 16 makes x = -2 an extraneous solution in the given equation.
To find the value of the constant "d" that makes x = -2 an extraneous solution in the equation √(6 - 15x) = 5x + d, we need to substitute x = -2 into the equation and check if it leads to any inconsistencies.
Let's substitute x = -2 into the equation:
√(6 - 15(-2)) = 5(-2) + d
√(6 + 30) = -10 + d
√36 = -10 + d
Now, we have two possible solutions for d, one with the positive square root and one with the negative square root:
√36 = 6:
6 = -10 + d
d = 6 + 10
d = 16
√36 = -6 (negative square root):
-6 = -10 + d
d = -6 + 10
d = 4
Now, let's check both solutions by substituting them back into the original equation:
For d = 16:
√(6 - 15x) = 5x + 16
Substituting x = -2:
√(6 - 15(-2)) = 5(-2) + 16
√(6 + 30) = -10 + 16
√36 = 6 (True)
For d = 4:
√(6 - 15x) = 5x + 4
Substituting x = -2:
√(6 - 15(-2)) = 5(-2) + 4
√(6 + 30) = -10 + 4
√36 = -6 (False)
Since the solution d = 4 leads to an incorrect result (extraneous solution), the correct value for the constant "d" that makes x = -2 an extraneous solution is:
d = 16
Learn more about the equations here:
brainly.com/question/10413253
#SPJ3
A game room has a floor that is 200 feet by 20 feet. A scale drawing of the floor on grid paper uses a scale of 2 units:5 feet. What are the dimensions of the scale drawing? Enter your answer as length by width.
Answers
Answer:
200 FEET
2 units/5 feet = x units/200 feet
x = 2/5 (200) = 400/5 = 80 units
Cross Multiplication
5x = 2(200)
x = 400/5 = 80 units
Step-by-step explanation:
given the a^b=x, evaluate the following.
a^b+2
Answers
Answer:
22+2
22+2
=6
Step-by-step explanation
hope this is right
josh is standing on the top of a building that is 425 feet tall. He throws a penny up into the air with an initial of 32 ft/sec. How long does it take for the penny to hit the ground?
Y = -4.9x^2 + 32x + 425
A. 10 seconds
B. 6.25
C. 400
D. 0 seconds
Answers
Answer:
A
Step-by-step explanation:
cause it will be more faster just because it is in a solid phase or it is solid
The time taken to hit the ground is 6.25 sec.(Option B)
How to calculate time?
It is given that penny follows the trajectory:
\(y = -4.9x^2 + 32x + 425\)
Differentiating it we get:
\(\dfrac{dy}{dx} =-9.8x+32\)
At y=425, it is obvious that x=0
So dy/dx at x=0 is 32.
Now the vertical component of the velocity is 32sinФ (where Ф is the angle at which penny is thrown).
Ф\(=\tan^{-1}(32)\)
Vertical component=\(32*\sin(\tan^{-1}(32))\)=31.98 ft/sec
Now applying the equation of motion: acceleration=-32ft/sec^(2)
u=31.98ft/sec s=-425 t=?
\(s=ut+\frac{1}{2} at^{2}\)
\(-425=31.98t-16t^2\)
\(16t^2-31.98t-425=0\)
Solving the quadratic equation we get:
t=6.249 sec≅6.25 sec
Therefore, the time taken is 6.25 sec.
To know more about equation of motion refer:https://brainly.com/question/24966506
#SPJ2
5 men and 12 boys finish a piece of work in 4 days, 7 men and 6 boys do it in 5 days. The ratio between the efficiencies of a man and boy is?.
Answers
According to the given statement 5 men and 12 boys finish a piece of work in 4 days, 7 men and 6 boys do it in 5 days. The ratio between the efficiencies of a man and a boy is 1 : 3.
To find the ratio between the efficiencies of a man and a boy, we need to compare the amount of work each man and each boy can do in a given time.
Let's assume that the efficiency of a man is M and the efficiency of a boy is B.
From the first scenario, we know that 5 men and 12 boys finish the work in 4 days.
This means that the combined efficiency of the 5 men is 5M and the combined efficiency of the 12 boys is 12B.
So, in 4 days, we have:
5M + 12B = 1
From the second scenario, we know that 7 men and 6 boys finish the work in 5 days.
This means that the combined efficiency of the 7 men is 7M and the combined efficiency of the 6 boys is 6B.
So, in 5 days, we have:
7M + 6B = 1
Now, we can solve these two equations simultaneously to find the values of M and B.
Multiply the first equation by 7 and the second equation by 5 to eliminate M:
35M + 84B = 7
35M + 30B = 5
Subtract the second equation from the first equation:
54B = 2
Divide both sides by 54:
B = 1/27
Now, substitute the value of B into any of the original equations to find M.
Let's use the first equation:
5M + 12(1/27) = 1
5M + 4/9 = 1
5M = 5/9
M = 1/9
Therefore, the ratio between the efficiencies of a man and a boy is:
M : B = (1/9) : (1/27)
To simplify the ratio, we can multiply both the numerator and denominator of the boy's efficiency by 3:
M : B = (1/9) : (3/27)
= 1 : 3
So, the ratio between the efficiencies of a man and a boy is 1 : 3.
To know more about ratio visit:
https://brainly.com/question/29134164
#SPJ11
For every 12 boy-days of work, a man completes 5 days in the first scenario. And in the second scenario, for every 6 boy-days of work, a man completes 7 days. The efficiency ratio between a man and a boy is:
First scenario: 5 men-days / 12 boy-days
Second scenario: 7 men-days / 6 boy-days
The efficiency of a person is measured by the amount of work they can complete in a given time. Let's find the efficiency ratio between a man and a boy.
In the first scenario, 5 men and 12 boys finish the work in 4 days. To find the total work done, we multiply the number of people by the number of days: (5 men + 12 boys) x 4 days = 20 men-days + 48 boy-days.
In the second scenario, 7 men and 6 boys finish the work in 5 days. Using the same logic, we get: (7 men + 6 boys) x 5 days = 35 men-days + 30 boy-days.
To find the efficiency ratio between a man and a boy, we can compare the work done by men to the work done by boys in both scenarios.
In the first scenario, the ratio of men's work to boys' work is 20 men-days : 48 boy-days.
In the second scenario, the ratio of men's work to boys' work is 35 men-days : 30 boy-days.
To simplify the ratios, we can divide the number of men-days and boy-days by their greatest common divisor (GCD). The GCD of 20 and 48 is 4, and the GCD of 35 and 30 is 5.
After dividing, we get the simplified ratio of men's work to boys' work:
First scenario: 5 men-days : 12 boy-days
Second scenario: 7 men-days : 6 boy-days
Learn more about efficiency
https://brainly.com/question/33283760
#SPJ11
continuing with problem 1, calculate the probability that the average sample weight is greater than 185 lbs when 15 participants are randomly selected for the sample? enter your answer rounded to two decimal places. do not enter % in the answer box. for example, if your answer is 0.12345 or 12.345% then enter as 12.35 in the answer box.
Answers
Answer:more context?
Step-by-step explanation:
The diameter of a circular pizza is 24 in. How much pizza is eaten (in square inches) if half of it is consumed? (Pie and л... hmmmm...interesting...)
Answers
Using the formula of area of a circle, about 226.08in² has been eaten
How much pizza is eaten?The diameter of the pizza is given as 24 inches. To calculate the area of the entire pizza, we need to use the formula for the area of a circle:
Area = π * r²
where π is approximately 3.14 and r is the radius of the circle.
Given that the diameter is 24 inches, the radius (r) would be half of the diameter, which is 12 inches.
Let's calculate the area of the entire pizza first:
Area = 3.14 * 12²
Area = 3.14 * 144
Area ≈ 452.16 square inches
Now, if half of the pizza is consumed, we need to calculate the area of half of the pizza. To do that, we divide the area of the entire pizza by 2:
Area of half of the pizza = 452.16 / 2
Area of half of the pizza ≈ 226.08 square inches
Therefore, if half of the pizza is consumed, approximately 226.08 square inches of pizza would be eaten.
Learn more on area of a circle here;
https://brainly.com/question/15673093
#SPJ1
USE ELIMINATION PLS! I WILL MAKE U BRAINLIST

Answers
Answer: (-4, -3) x= -4 y=-3
Step-by-step explanation:
2x-y=-15
-2x-4y= 30
x is already eliminated
-5y=15
/-5
y=-3
now plug in y to one of equations
2x+3=-15
-3 -3
2x=-8
/2
x=-4