Answers
Answer: kinda
Step-by-step explanation:
as long as you have a passing grade you will be fine, just work on the "F" :)
Related Questions
A bridge, PR, across a river is 400 m long. Gabe is launching a canoe at point Q.
He will paddle in a diagonal line across the river to point P. He plans to return along a route beside the bridge from P to R, and then along the shore from R back to Q. How far will this be altogether?
Answers
Therefore, the total distance Gabe will paddle is 2x + 400 meters. The exact value of x depends on the width of the river, which is not provided in the given information.
To find the total distance Gabe will paddle, we need to consider the distance he will travel from Q to P, then from P to R, and finally from R back to Q.
First, let's consider the distance from Q to P. Since Gabe will paddle in a diagonal line across the river, this distance can be calculated using the Pythagorean theorem.
The length of the bridge (PR) is given as 400 meters, which is the hypotenuse of a right triangle. The width of the river can be considered as the perpendicular side, and the distance Gabe will paddle from Q to P is the other side. Let's call this distance x.
Using the Pythagorean theorem, we have:
x^2 + (width of the river)^2 = PR^2
Since the width of the river is not given, we'll represent it as w. Therefore:
x^2 + w^2 = 400^2
Next, let's consider the distance from P to R. Gabe will paddle along a route beside the bridge, which means he will travel the length of the bridge (PR) again. So, the distance from P to R is also 400 meters.
Finally, Gabe will paddle back from R to Q along the shore. Since he will follow the shoreline, the distance he will paddle is equal to the distance from Q to P, which is x.
To find the total distance, we add up the distances:
Total distance = QP + PR + RQ
= x + 400 + x
= 2x + 400
For more suchy questions on distance visit:
https://brainly.com/question/28551043
#SPJ8
A 4500 square foot roll of plastic wrap costs $23.95. If 120 square feet is need for a party game, what is the monetary value of that 120 square foot piece of plastic wrap? Round to the nearest cent.
Answers
$0.64 is the monetary value.
We are given that a 4500 square foot roll of plastic wrap costs $23.95 and we are to determine the monetary value of a 120 square foot piece of plastic wrap.
Let us find the cost per square foot by dividing the total cost of the roll by the number of square feet in the roll:
$23.95/4500 = $0.005322 per square foot
Now, we can multiply the cost per square foot by the number of square feet needed for the party game (120) to find the monetary value of the piece of plastic wrap.
Therefore, the monetary value of that 120-square-foot piece of plastic wrap is:
$0.005322 x 120 = $0.64 (rounded to the nearest cent)
Hence, the monetary value of that 120-square-foot piece of plastic wrap is $0.64.
Learn more about area:
https://brainly.com/question/28948613
#SPJ11
Lots of points
For the line segment whose endpoints are L (0, 1) and M (2, 8), find the y coordinate for the point located 3 over 5 the distance from L to M.
5. 2
3. 5
4. 8
1. 6
Answers
The y-coordinate for the point located 3/5 the distance from L to M is 6.
A line segment is a part of a line that extends between two endpoints. The length of a line segment can be calculated by determining the difference between the coordinates of the endpoints of the line segment, both horizontally (the x-coordinates) and vertically (the y-coordinates).
Using these information, we will find the coordinates of a point which is 3/5 of the distance from L to M.
The distance between L(0,1) and M(2,8) is calculated as follows:
d(L, M) = √[(8 - 1)² + (2 - 0)²] = √65.
To determine the x-coordinate of the point 3/5 of the way from L to M, we can use the formula:
x = x₁ + (3/5)(x₂ - x₁) = 0 + (3/5)(2 - 0) = 1.2
To determine the y-coordinate of the point, we can use the formula:
y = y₁ + (3/5)(y₂ - y₁) = 1 + (3/5)(8 - 1) = 6
Therefore, the y-coordinate of the point 3/5 of the way from L to M is 6.
Learn more about line segment from the given link
https://brainly.com/question/280216
#SPJ11
The food company is now designing soup cans. They currently make a large can of soup that holds 24oz of soup. They would like to make a single serve can that holds only 8oz of soup. The large can has a surface area of 100.48in². What will the new single serving surface area be? Explain or show your reasoning.
Answers
The surface area of the new single-serving soup can, with a volume ratio of 24:8, will be approximately 11.164 square inches.
To determine the surface area of the new single-serving soup can, we can use the concept of ratios and proportions.
Let's assume the radius of the large can is represented by R and the radius of the single-serving can is represented by r.
The volume of a cylinder can be calculated using the formula V = πr^2h, where V is the volume, r is the radius, and h is the height.
We know that the large can has a volume of 24oz, so we have:
24 = πR^2h
Now, we need to find the height of the single-serving can. Since the large can and the single-serving can have the same height (we assume), we can set up a ratio of their volumes:
24/8 = πR^2h / πr^2h
Simplifying the equation, we have:
3 = (R^2h) / (r^2h)
Since the height cancels out, we can rewrite the equation as:
3 = R^2 / r^2
To find the ratio of the surface areas, we square both sides of the equation:
9 = (R^2 / r^2)^2
Now, we can find the surface area ratio:
100.48 / A = 9
Solving for A (the surface area of the single-serving can), we have:
A = 100.48 / 9
Calculating the value, we find that the new single-serving surface area will be approximately 11.164 in².
Therefore, the new single-serving soup can will have a surface area of approximately 11.164 square inches.
For more question on surface area visit:
https://brainly.com/question/16519513
#SPJ8
triangle MNO has vertices at (-3,-8), (2,-8) and (0,-15). translate it up 8 units.
Answers
Answer:
(-3,0) (2,0) (0,-7)
Step-by-step explanation:
Up and Right are addition and Left and Down are subtraction. add 8 to the y coordinates.
Click on the volume of this rectangular prism.
6 cm
9cm
12cm
Answers
Answer:
648 , just multiple all the numbers together
The coordinates of the midpoint of gh are m(-13/2,-6) and the coordinates of one endpoint are g(-4,1). what is the other endpoint?
Answers
Applying the midpoint formula, the coordinates of the other endpoint are: (-9, -13).
How to Apply the Midpoint Formula?The midpoint formula, which can be used in determining the coordinates of the midpoint between two endpoints is usually expressed as: M[(x1 + x2)/2, (y1 + y2)/2].
Given the following coordinates:
Midpoint of GH --> m(-13/2,-6) = (x, y)
One endpoint ---> G(-4, 1) = (x1, y1)
The other endpoint ---> (x2, y2)
Plug in the values into the formula used in calculating the midpoint:
m(-13/2,-6) = [(-4 + x2)/2, (1 + y2)/2]
Solve for x2
-13/2 = (-4 + x2)/2
-13/2 × 2 = -4 + x2
-13 = -4 + x2
-13 + 4 = x2
-9 = x2
x2 = -9
Solve for y2
-6 = (1 + y2)/2
2(-6) = 1 + y2
-12 = 1 + y2
-12 - 1 = y2
-13 = y2
y2 = -13
Thus, using the midpoint formula, the coordinates of the other endpoint are: (-9, -13).
Learn more about the midpoint formula on:
https://brainly.com/question/13115533
#SPJ1
When will the integral\oint \vec{E}\cdot d\vec{l}aroundany closed loop of the projection of the electric field along thatloop be zero?
a. only if the field is generated by the coulombfield of static charges
b. only if the field is generated by the coulombfield of static charges or a constant current
c. only if the field is generated by a changingmagnetic field
d. however the field is generated
e. The loop integral is always zero; otherwise, acharge moving around the loop would gain energy.
Answers
The correct answer is option B: only if the field is generated by the Coulomb field of static charges or a constant current. This is because in both cases, the electric field is conservative, meaning that the work done by the field on a charge moving along a closed loop is zero.
This can be expressed mathematically as the integral of the electric field along a closed loop being equal to zero.
Option A is incorrect because while the Coulomb field of static charges is conservative, not all static fields are. Option C is incorrect because a changing magnetic field generates a non-conservative electric field, and option D is incorrect because not all fields are conservative.
Option E is not entirely correct because while the loop integral of a conservative field is zero, it is not true that a charge moving around the loop would gain energy if the loop integral were non-zero. The loop integral represents the work done by the field on the charge, and the gain or loss of energy depends on other factors such as the direction and magnitude of the charge's velocity.
to learn more about electric field, refer:-
https://brainly.com/question/30173473
#SPJ11
in the xy-plane, which of the following is an equation of a vertical asymptote to the graph Of y=sec(6x-pi)? (A) x=pi/6 (B) x=pi/4 (C) x=pi/3 (D)=x=pi/2 (E) x=pi
Answers
The equation of a vertical asymptote to the graph of y = sec(6x - π) is x = π/6. Hence, option a is correct.
The function y = sec(6x - π) has vertical asymptotes at the values of x where the denominator of sec(6x - π) becomes zero. The reciprocal of sec(θ) is cos(θ). Because the cosine function has the values π/2, 3π/2, 5π/2, we will insert such an input that we get 0 in denominator.
6x - π = π/2
Solving for x,
6x = π/2 + π
6x = 3π/2
x = (3π/2) / 6
x = π/6
Therefore, the equation of a vertical asymptote to the graph of y = sec(6x - π) is x = π/6.
To know more about asymptotes, visit,
https://brainly.com/question/4138300
#SPJ4
True or False: For a given mass of rising air, the dry adiabatic rate will always be higher than the wet adiabatic rate.
Answers
Answer:
true
Step-by-step explanation:
because there's less humidity
NO. 1: (4 marks)
For a laboratory assignment, if the equipment is workingthe density function of the observed outcome X is
f(x)= 2(1 - x) ,\\ 0, 0 < x < 1
otherwise.
Find the variance and standard deviation of X.
Var(X) = E(X)-(E(X)
Answers
The standard deviation is equal to the square root of the variance, which is √(1/8) ≈ 0.353.
To find the variance and standard deviation of X with the given density function, we need to calculate the expected value (E(X)) and the expected value of X squared (E(X^2)). Then, we can use the formula Var(X) = E(X^2) - [E(X)]^2 to find the variance.
First, let's calculate E(X):
E(X) = ∫(x * f(x)) dx
= ∫(x * 2(1 - x)) dx
= 2∫(x - x^2) dx
= 2[x^2/2 - x^3/3] + C
= x^2 - (2/3)x^3 + C
Next, let's calculate E(X^2):
E(X^2) = ∫(x^2 * f(x)) dx
= ∫(x^2 * 2(1 - x)) dx
= 2∫(x^2 - x^3) dx
= 2[x^3/3 - x^4/4] + C
= (2/3)x^3 - (1/2)x^4 + C
Now, we can find the variance:
Var(X) = E(X^2) - [E(X)]^2
= [(2/3)x^3 - (1/2)x^4 + C] - [x^2 - (2/3)x^3 + C]^2
= [(2/3)x^3 - (1/2)x^4] - [x^2 - (2/3)x^3]^2
The standard deviation can be calculated as the square root of the variance.
To learn more about standard deviation click here
brainly.com/question/29115611
#SPJ11
Complete Question
For a laboratory assignment, if the equipment is working, the density function of the observed outcome X is
f(x) = 2 ( 1 - x ), 0 < x < 1
0 otherwise
(1) Find the Variance and Standard deviation of X.
6th grade math !!!!!!!!!!!!!!
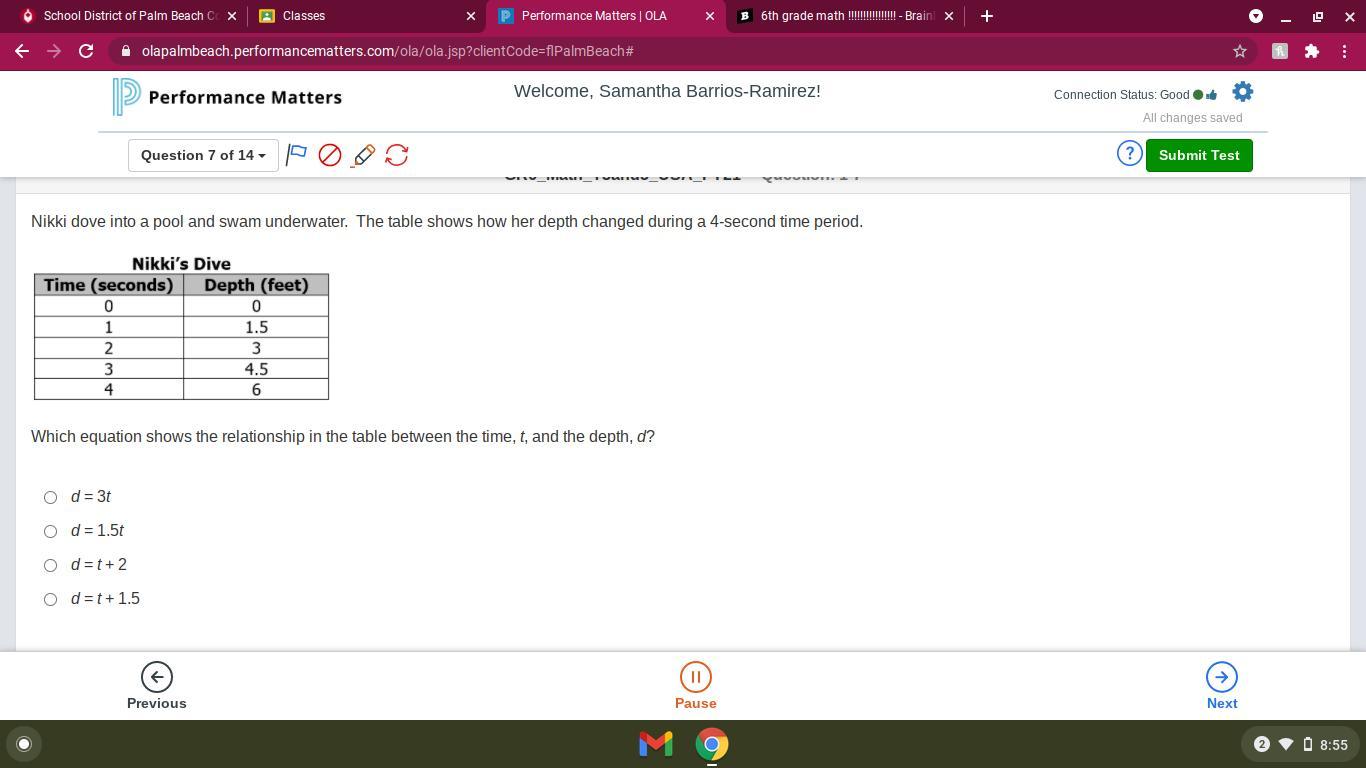
Answers
Answer: It's the second option
Step-by-step explanation:
0x1.5=0
1x1.5=1.5
2x1.5=3
3x1.5=4.5
4x1.5=6
It's simple math
Hope this helped
Can someone help me with this question please

Answers
30. In the figure below, rectangle ABCD shares CD with ACDE,
diagonal BD of the rectangle extends in a straight line
beyond D to E to create DE, and the measure of CDE is
155°.
What is the measure of ZCBD?
F. 25
G.55
H.65
J.90
K.155

Answers
The measure of angle ZCBD is 90°. Therefore, the correct option is J. 90.
To find the measure of angle ZCBD, we need to examine the given information.
From the figure, we know that angle CDE is 155°.
Since the opposite angles of a rectangle are congruent, angle BCD is also 155°.
In a rectangle, the sum of the interior angles at a vertex is always 90°.
Therefore, angle CBD is 90°.
Hence, the measure of angle ZCBD is 90°.
Therefore, the correct option is J. 90.
for such more question on measure of angle
https://brainly.com/question/25716982
#SPJ8
Solve the following equation algebraically 2x ^ 2 = 50
Answers
Answer:
x=5
Step-by-step explanation:
\(2 {x}^{2} = 50\)
\( {x}^{2} = \frac{50}{2} \)
\( {x}^{2} = 25\)
\(x = \sqrt{25} \)
\(x = 5\)
An arc spans a central angle that is \dfrac{3\pi}{5}
5
3π
start fraction, 3, pi, divided by, 5, end fraction radians.
What fraction of the circumference is this arc?
Answers
Answer:
what does \dfrac mean
Step-by-step explanation:
I'm only in 11th grade and I don't know anything of this cuz I'm dum
Tony has 1.44 lb of cheese. He needs 0.08 lb of cheese for one sandwich. How many sandwiches can he make?
Answers
Total weight of cheese = 1.44 lb
Weight of cheese for one sandwich = 0.08 lb
Number of sandwiches you can make from 1.44 lb
= 1.44/0.08
= 18 sandwiches
The sum of the ages of Alice, Barbie & Cindy is 44. Alice is three times older than Cindy. Barbie is 5 years younger than Alice. How old is Cindy?
Answers
Answer: Cindy is 7
Step-by-step explanation:
Alice is 21
Barbie is 16
Natalie did 87 sit-ups in 3 minutes.
What is the unit rate?
At this rate, how many sit-ups can Natalie do in 5 minutes?
Answers
Answer:
19 sit-ups per minute ;
95 sit-ups
Step-by-step explanation:
Given that :
Number of sit-ups done in 3 minutes = 57
The unit rate of sit-ups done can be obtained thus :
Total Number of sit-ups done / total time taken
= 57 sit-ups /3 minutes
= 19 sit-ups per minute
. Number of sit-ups that can be done in 5 minutes :
Unit Rate of sit-ups * number of minutes
19 sit-ups / minute * 5 minutes
= 95 (sit-ups / minute * minute)
= 95 sit-ups
After 14 years, I shall be three times as old as I was 4 years ago. What is my present age?
Answers
Answer:
Present age = 13 years
Step-by-step explanation:
Let the present age be x years.
14 years after age = (x + 14) years
4 years ago age = (x - 4)
According to the given information:
14 years after age = 3 times 4 years ago age
x + 14 = 3(x - 4)
x + 14 = 3x - 12
14 + 12 = 3x - x
26 = 2x
x = 26/2
x = 13 years
Thus, the present age is 13 years
Laura is on her way home in her car. She has driven 6 miles so far, which is two-thirds of the way home. What is the total length of her drive?1 milesх5?
Answers
Let
x ------> distance way home
we have that
(2/3)x=6
solve for x
x=6*3/2
x=9 miles
therefore
the answer is 9 milesGiven the figure, find the values of x and z.
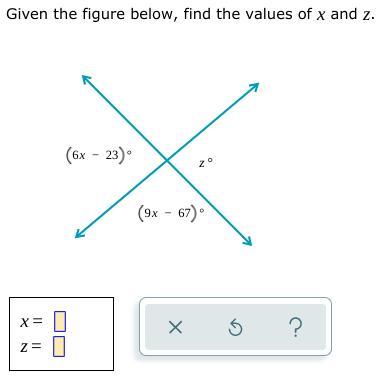
Answers
The angle with (6x-23) and (9x-67) together make a straight line, so their sum is 180:
(6x-23) + (9x-67) = 180
So you need to solve that for x.
For z, z and (6x-23) are vertical angles, so their angle measures are the same.
z = 6x-23
\(\\ \sf\bull\dashrightarrow 9x-67+6x-23=180\)
\(\\ \sf\bull\dashrightarrow 9x+6x-67-23=180\)
\(\\ \sf\bull\dashrightarrow 15x-90=180\)
\(\\ \sf\bull\dashrightarrow 15x=180+90=270\)
\(\\ \sf\bull\dashrightarrow x=18\)
Now
\(\\ \sf\bull\dashrightarrow z=6x-23\)
\(\\ \sf\bull\dashrightarrow z=18(6)-23\)
\(\\ \sf\bull\dashrightarrow z=108-23\)
\(\\ \sf\bull\dashrightarrow z=85\)
URGENT PLEASE HELP: find the musing value of x round to the nearest tenth

Answers
formula 1\2 bh
1\2 (63×16)+x =180
1\2 (1008) +x =180
504+x=180
x= 504-180
x= 36.2
for the following conjecture, state the null and alternative hypotheses. the average weight loss for a sample of people who exercise 30 minutes per day for 6 weeks is greater than 8.2 pounds.
Answers
For the given conjecture, which is "the average weight loss for a sample of people who exercise 30 minutes per day for 6 weeks is greater than 8.2 pounds", the null and alternative hypotheses can be stated as follows:
Null Hypothesis (H0): The average weight loss for the sample is equal to or less than 8.2 pounds (≤ 8.2 lbs).
Alternative Hypothesis (H1): The average weight loss for the sample is greater than 8.2 pounds (> 8.2 lbs).
These hypotheses are formed to test whether there is significant evidence to support the conjecture that exercising 30 minutes per day for 6 weeks leads to an average weight loss of more than 8.2 pounds.
Learn more about hypotheses here:
https://brainly.com/question/18064632
#SPJ11
Dyani began solving the equation g = x-1/k for x by using the addition property of equality. explain dyani's error. then describe how to solve for x
Answers
Given equation g = x-1/k in terms of x would be x = 1 + gk
for given question,
we have been given an equation g = x-1/k
Dyani began solving the equation g = x-1/k for x by using the addition property of equality.
We solve given equation for x.
⇒ g = x-1/k ..........(Given)
⇒ gk = (x - 1/k)k .........(Multiply both the sides by k)
⇒ gk = x - 1
⇒ gk + 1 = x - 1 + 1 .........(Add 1 to each side)
⇒ gk + 1 = x
⇒ x = 1 + gk
Therefore, given equation g = x-1/k in terms of x would be x = 1 + gk
Learn more about an equation here:
https://brainly.com/question/649785
#SPJ4
Which relationship describes angles 1 and 2?
complementary angles
supplementary angles
vertical angles
adjacent angles

Answers
The relationship that describes angles 1 and 2 are vertical angles.
What are vertical angles?
Vertical angles are angles opposite each when two lines cross each other. A supplementary angle is an angle that adds up to 180. A complementary angle adds up to 90 degrees.
Find f(-3) if f(x) = x^2
6
-9
9
-6
Answers
Answer:
B. -9
Step-by-step explanation:
The equation would be f(-3)=-3^2
3*3 is 9
Add the - back on, and you get -9
I hope this helps!
Prove that for any matrices M,N such that MN is well-defined, rank(MN)≤min{rank(M), rank(N)}. (hint: to start, remember that each column of the matrix AB is a linear combination of the columns of A)
Answers
We have proven that for any matrices M and N such that MN is well-defined, rank(MN) ≤ min{rank(M), rank(N)}.
To prove the statement "rank(MN) ≤ min{rank(M), rank(N)}," we can utilize the fact that each column of the matrix MN is a linear combination of the columns of M.
Let's assume M is an m × n matrix and N is an n × p matrix. The product MN will be an m × p matrix.
Let C(M) and C(MN) denote the column spaces of M and MN, respectively. We want to show that dim(C(MN)) ≤ min{dim(C(M)), dim(C(N))}.
Consider an arbitrary column vector u in C(MN). Since u is in the column space of MN, we can express it as a linear combination of the columns of MN:
u = MNv,
where v is a p-dimensional vector.
Since each column of MN is a linear combination of the columns of M, we can express v as a linear combination of the columns of M:
v = My,
where y is an n-dimensional vector.
Substituting this expression for v into the equation u = MNv, we get:
u = MN(My) = (MN)My.
Notice that (MN)My is a linear combination of the columns of MN. Therefore, u is also a linear combination of the columns of MN, implying that u is in C(MN).
We have shown that any column vector u in C(MN) is also in C(MN). This implies that the column space of MN is a subset of the column space of M, i.e., C(MN) ⊆ C(M).
By the same reasoning, we can show that C(MN) ⊆ C(N).
Hence, we have:
dim(C(MN)) ≤ dim(C(M)) (since C(MN) ⊆ C(M))
dim(C(MN)) ≤ dim(C(N)) (since C(MN) ⊆ C(N))
Taking the minimum of both sides, we obtain:
dim(C(MN)) ≤ min{dim(C(M)), dim(C(N))}
Recalling that rank(M) = dim(C(M)) and rank(N) = dim(C(N)), we have:
rank(MN) ≤ min{rank(M), rank(N)}
Therefore, we have proven that for any matrices M and N such that MN is well-defined, rank(MN) ≤ min{rank(M), rank(N)}.
To learn more on matrix click:
brainly.com/question/28180105
#SPJ4
Rectangle ABCD was dilated to create rectangle A'B'C'D. Triangle A B C D is dilated to form triangle A prime B prime C prime D. Side B C is 3.8 units. Side A prime B prime is 15 units and side B prime C prime is 9.5 units. What is AB? 6 units 7.6 units 9.5 units 12 units
Answers
Answer:
\(AB = 6\)
Step-by-step explanation:
Given
\(BC = 3.8\)
\(A'B' = 15\)
\(B'C' = 9.5\)
Required
Determine the length of AB
Because A'B'C'D is a dilation of ABCD, then the following relationship must exist:
\(A'B' : AB = B'C' : BC\)
Substitute values for A'B', B'C' and BC
\(15 : AB = 9.5 : 3.8\)
Express the ratio as fractions:
\(\frac{AB}{15} = \frac{3.8}{9.5}\)
Multiply through by 14
\(15 * \frac{AB}{15} = \frac{3.8}{9.5} * 15\)
\(AB = \frac{3.8}{9.5} * 15\)
\(AB = \frac{3.8* 15}{9.5}\)
\(AB = \frac{57}{9.5}\)
\(AB = 6\)
Answer:
A. 6 units
Step-by-step explanation:
I got it right on edge.
2) A big league pitching coach tries to limit his pitchers to 110
pitches per game. If the pitcher has already thrown 52
pitches, write and solve an inequality to find how many more
pitches he can throw before reaching the limit.
