Apr 17, 7:54:37 PM
Watch help video
Which of the following sets of numbers could represent the three sides of a right
triangle?
O {14, 20, 25}
O {64, 72,97}
O {32, 60, 68}
O {45, 59, 75}
Answers
The sets of number that represent the three sides of the right triangle are {32, 60, 68}.
How to find the sides of a right angle triangle?A right angle triangle is a triangle that has one of its angles as 90 degrees. The sum of angles in a triangle is 180 degrees.
A right angle triangle follows Pythagoras's theorem. The Pythagorean triple is as follows:
a² + b² = c²
where
a and b are the legsc is the hypotenuse sideTherefore,
32² + 60² = 68²
1024 + 3600 = 4624
4624 = 4624
Therefore, the sets of number that represents the three sides of the right triangle is {32, 60, 68}
learn more on right triangle here: https://brainly.com/question/28990225
#SPJ1
Related Questions
Please help right now (30 points if you’re interested) The table shows the ratio between the number of books ordered and their cost. 7,14 8,16 9,18. Find equivalent ratios when the number of books ordered is 1,2, and 3. Write them as ordered pairs in the form (x-coordinate, y-coordinate). Starting from the origin explain how to plot three equivalent ratios on a coordinate grid.

Answers
The equivalent ratios are: (1, 2), (2, 4), and (3, 6)
The graph can be plotted on a coordinate grid as shown in the diagram attached below.
Recall:
Ratio between two quantities, x and y, can be represented by the equation, y = kx, where k is the constant of proportionality.k = y/xLet x = number of books
y = cost (dollars)
Using any of the ordered pairs from the table, say, (7, 14), find k:
k = y/x = 14/7 = 2
Write the equation by plugging in the value of k into y = kx
y = 2x
Using the equation, y = 2x, find the equivalent ratios when x = 1, x = 2, and x = 3:
When x = 1:
y = 2(1) = 2 --> (1, 2)
When x = 2:
y = 2(2) = 4 ---> (2, 4)
When x = 3:
y = 2(3) = 6 ---> (3, 6)
The graph for the three equivalent ratios, (1, 2), (2, 4), and (3, 6) can be plotted on a coordinate grid as shown in the diagram attached below.
Learn more about equivalent ratio on:
https://brainly.com/question/2914376

Create a data set with 6 different values whose mean is 100
Answers
Answer:
70, 85, 93, 100, 125, and 127
Explanation:
We want to create a data set with 6 different values whose mean is 100.
Let the sum of the 6 numbers = x
\(\begin{gathered} \frac{x}{6}=100 \\ \implies x=6\times100 \\ x=600 \end{gathered}\)What this means is that the 6 numbers must add up to 600.
Let 5 numbers in the data set be:
• 70, 93, 100, 125, and 127
Add the 5 numbers up:
\(70+93+100+125+127=515\)Subtract the sum from 600 to get the 6th number.
\(600-515=85\)Thus, the 6 diffrent values are:
\(70,85,93,100,125,\text{ and }127\)
I need some help please?

Answers
Answer:
C choice.
Step-by-step explanation:
Since line a is given a slope as -4.
Another line which is line b is given that it's perpendicular to line a or we can say that line a is perpendicular to line b.
Perpendicular is defined as:
\( \displaystyle \large{m_1m_2 = - 1}\)
Both slopes multiply and yield -1.
We know that m1 is -4; we want to find m2 which is slope of line b.
\( \displaystyle \large{ - 4m_2 = - 1}\)
Divide both sides by -4.
\( \displaystyle \large{ \frac{ - 4m_2}{ - 4} = \frac{ - 1}{ - 4} } \\ \displaystyle \large{ m _2 = \frac{1}{4} }\)
Therefore, the slope for line b is 1/4.
Thus, the C choice is correct.
What is the solution to the system of equations? 2x - 2y = -2; x + 3y = 15
Answers
Answer: x=3 and y=4
Step-by-step explanation:
Rewrite equations:
x+3y=15;2x−2y=−2
Step: Solve x+3y=15 for x:
x+3y=15
x+3y+−3y=15+−3y(Add -3y to both sides)
x=−3y+15
Step: Substitute−3y+15 for x in 2x−2y=−2:
2x−2y=−2
2(−3y+15)−2y=−2
−8y+30=−2(Simplify both sides of the equation)
−8y+30+−30=−2+−30(Add -30 to both sides)
−8y=−32
−8y over −8 = −32 over −8
(Divide both sides by -8)
y=4
Step: Substitute 4 for y in x=−3y+15:
x=−3y+15
x=(−3)(4)+15
x=3(Simplify both sides of the equation)
Johnny is given 18 bottles of beer and he drinks 6 of them. How much beer does Johnny have left?
Answers
Answer: 12 bottles left
Step-by-step explanation:
18-6=12 bottles
Answer:
Johnny will have 7 beer bottles left.
Step-by-step explanation:
A square stepping stone has a side length of 10 1/4 inches.
What is the area of the stepping stone?
Answers
Area=2.5
Step-by-step explanation:
area
\(area = length \times width\)
\(area = 10 \times \frac{1}{4} \)
If one side = 10 1/4 inches = 10.25 inch
Then
Area = 4* 10.25 = 41 inches^2
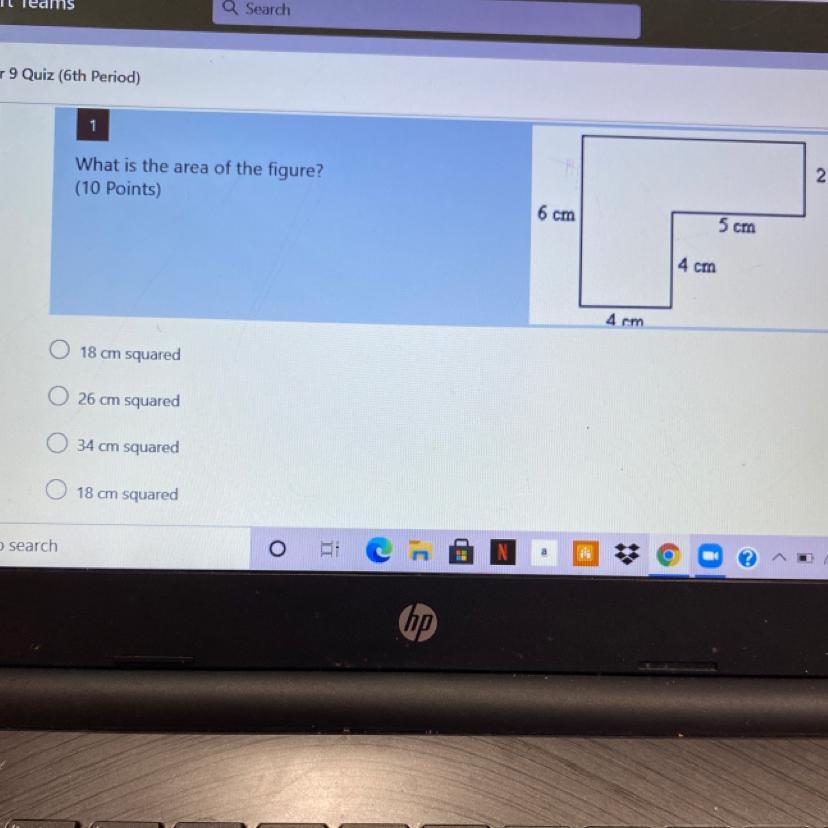
2 cm
What is the area of the figure?
(10 Points)
6 cm
5 cm
4 cm
4 cm
18 cm squared
26 cm squared
34 cm squared
18 cm squared
e to search
d
1:50 PM
2/23/2021
hp)
Answers
Answer:
34 cm squared
Step-by-step explanation:
You would need to fill in the cut out part of the shape. Find the area of the whole shape minus the area of the cut out shape.
Area of the bigger shape :6*9 =54cm squared
Area of the cut out shape:4*4=20cm squared
Area of the whole shape is 54 - 20 = 34cm squaredAjar contains 24 blue marbles, 16 red marbles, and 14 white marbles. Find the simplified ratio
of total marbles to red marbles.
Answers
Answer:
Answer: 27:8
Step-by-step explanation:
There are 24 + 16 + 14 = 24+16+14= 54
54 marbles in total.
The ratio of total marbles to red marbles is 54 : 16, which simplifies to 27 : 8.
Answer: 27:8
what is 1 and 2/5 as an improper fraction
Answers
Answer:
\(\displaystyle 1\frac{2}{5}=\frac{7}{5}\)
Step-by-step explanation:
\(\displaystyle a\frac{b}{c}=\frac{ac+b}{c}\\\\1\frac{2}{5}=\frac{(1)(5)+2}{5}=\frac{5+2}{5}=\frac{7}{5}\)
What is the area of the triangle 7mm and 8mm

Answers
Answer:
the area of triangle
\( \frac{1}{2} \times base \times height \\ → \frac{1}{2} \times 8 \times 7 \\→ 4 \times 7 = 28 {mm}^{2} \)
Step-by-step explanation:
hope it helps you<3John is saving to buy a new car that will cost him $24,000. John started his savings at the beginning of the school year and has been able to accumulate $1000 after the first month. John plans to continue his savings at a rate proportional to the amount he still needs to save. Determine John's savings amount as function of time Hint: A variable y is said to be proportional to a variable x if y=cx for some constant c.
Answers
John's savings amount as a function of time is S(t) = $24,000 / 25. Initially, he needs to save $24,000 for a new car. After the first month, he has saved $1,000. The savings amount is directly proportional to the time elapsed. The constant of proportionality is 1/24. Thus, John's savings amount can be determined based on the remaining amount he needs to save.
John's savings amount can be represented as a function of time and is proportional to the amount he still needs to save. Let's denote the amount John needs to save as N(t) at time t, and his savings amount as S(t) at time t. Initially, John needs to save $24,000, so we have N(0) = $24,000.
We know that John has saved $1,000 after the first month, which means S(1) = $1,000. Since his savings amount is proportional to the amount he still needs to save, we can write the proportionality as:
S(t) = k * N(t)
where k is a constant of proportionality.
We need to find the value of k to determine John's savings amount at any given time.
Using the initial values, we can substitute t = 0 and t = 1 into the equation above:
S(0) = k * N(0) => $1,000 = k * $24,000 => k = 1/24
Now we have the value of k, and we can write John's savings amount as a function of time:
S(t) = (1/24) * N(t)
Since John's savings amount is proportional to the amount he still needs to save, we can express the amount he still needs to save at time t as:
N(t) = $24,000 - S(t)
Substituting the expression for N(t) into the equation for S(t), we get:
S(t) = (1/24) * ($24,000 - S(t))
Simplifying the equation, we have:
24S(t) = $24,000 - S(t)
25S(t) = $24,000
S(t) = $24,000 / 25
Therefore, John's savings amount at any given time t is S(t) = $24,000 / 25.
To know more about proportional savings, refer here:
https://brainly.com/question/29251832#
#SPJ11
Find the length of side x simplest radical form with a rational denominator

Answers
Answer:
The length of x in the simplest radical form with a rational denominator will be:
\(x=\frac{5\sqrt{3}}{2}\)Step-by-step explanation:
Given
hypotenuse = 5
angle Ф = 60°
To determine
x = ?
Using the trigonometric ratio
cos Ф = adjacent / hypotenuse
here
Ф = 60°
adjacent of 60° = x
hypotenuse = 5
so substituting Ф = 60°, adjacent = x and hypotenuse = 5 in the equation
cos Ф = adjacent / hypotenuse
so
\(cos\:60^{\circ }\:=\:\frac{x}{5}\)
\(\frac{\sqrt{3}}{2}=\frac{x}{5}\)
switch sides
\(\frac{x}{5}=\frac{\sqrt{3}}{2}\)
Multiply both sides by 5
\(\frac{5x}{5}=\frac{5\sqrt{3}}{2}\)
Simplify
\(x=\frac{5\sqrt{3}}{2}\)
Therefore, the length of x in the simplest radical form with a rational denominator will be:
\(x=\frac{5\sqrt{3}}{2}\)a water tank can be filled by two pipes working together in 2 hours. one of the pipes can fill the tank in 3 hours less than the other pipe. how long does each pipe take to fill the tank on its own?
Answers
Let's denote the time it takes for the slower pipe to fill the tank on its own as $x$ hours. Then, the faster pipe takes $x-3$ hours to fill the tank on its own. We can use the formula for the rate of work to set up an equation: $r_1 + r_2 = \frac{1}{2}$, where $r_1$ and $r_2$ are the rates of work for each pipe.
We can express the rate of work in terms of the time it takes for each pipe to fill the tank on its own: $r_1 = \frac{1}{x}$ and $r_2 = \frac{1}{x-3}$. Substituting these expressions into the equation above and solving for $x$, we obtain $x=2$. Therefore, the slower pipe takes 2 hours to fill the tank on its own, and the faster pipe takes $2-3=-1$ hour, which doesn't make physical sense. This means there is an error in the problem statement.
To learn more about equation : brainly.com/question/29657983
#SPJ11
Find the area of the shaded region.

Answers
An.swer:
171.68
Step-by-step explanation:
A bank loan processing system has three components with individual reliabilities as shown: R 1 = 0.82 R 2 = 0.991 R 3 = 0.98 What would be the reliability of the bank system above if each of the three components had a backup with a reliability of 0.80? How would the total reliability be different?
Answers
To calculate the reliability of the bank loan processing system with backup components, we can use the concept of series-parallel system reliability.
In the original system, the three components are connected in series. To calculate the overall reliability of the system, we multiply the reliabilities of the individual components:
R_system = R_1 * R_2 * R_3 = 0.82 * 0.991 * 0.98 ≈ 0.801
So, the reliability of the bank loan processing system without backup components is approximately 0.801.
Now, if each of the three components has a backup with a reliability of 0.80, we have a parallel configuration between the original components and their backups. In a parallel system, the overall reliability is calculated as 1 minus the product of the complement of individual reliabilities.
Let's calculate the reliability of each component with the backup:
R_1_with_backup = 1 - (1 - R_1) * (1 - 0.80) = 1 - (1 - 0.82) * (1 - 0.80) ≈ 0.984
R_2_with_backup = 1 - (1 - R_2) * (1 - 0.80) = 1 - (1 - 0.991) * (1 - 0.80) ≈ 0.9988
R_3_with_backup = 1 - (1 - R_3) * (1 - 0.80) = 1 - (1 - 0.98) * (1 - 0.80) ≈ 0.9992
Now, we calculate the overall reliability of the system with the backups:
R_system_with_backup = R_1_with_backup * R_2_with_backup * R_3_with_backup ≈ 0.984 * 0.9988 * 0.9992 ≈ 0.981
Therefore, the reliability of the bank loan processing system with backup components is approximately 0.981.
Comparing the two scenarios, we can see that introducing backup components with a reliability of 0.80 has improved the overall reliability of the system. The total reliability increased from 0.801 (without backups) to 0.981 (with backups). Having backup components in a parallel configuration provides redundancy and increases the system's ability to withstand failures, resulting in higher reliability.
Learn more about approximately here:
https://brainly.com/question/31695967
#SPJ11
Theatre tickets cost either $30 or $42. One evening twice as many $30 tickets are sold as $42 tickets and the total money taken is $18564. Find the total number of tickets that are sold.
Answers
1 + 2 = 3
18564 / 3 = 6188
6188 x 2 = 12376
Ratio = 6188:12376
6188 / 42 = 148 tickets
12376 / 30 = 413 tickets
413 + 148 = 561 tickets
✨Solve each equation by factoring
PLS HELPPPPP N SHOW UR WORKKK TOO✨✨✨

Answers
Answer:
choice c is correct
Step-by-step explanation:
b^2 -15b +56 = 0
b^2-8b-7b +56 = 0
b(b-8) -7(b-8) = 0
(b-8)(b-7) = 0
b= {8, 7}
Which equation is an identity

Answers
can someone help please

Answers
When Tracey pours all the water from the smaller 5-inch cube container into the larger 7-inch cube container, the water will be approximately 7 inches deep in the larger container.
To find out how deep the water will be in the larger container, we need to consider the volume of water transferred from the smaller container. Since both containers are cube-shaped, the volume of each container is equal to the length of one side cubed.
The volume of the smaller container is 5 inches * 5 inches * 5 inches = 125 cubic inches.
When Tracey pours all the water from the smaller container into the larger container, the water completely fills the larger container. The volume of the larger container is 7 inches * 7 inches * 7 inches = 343 cubic inches.
Since the water fills the larger container completely, the depth of the water in the larger container will be equal to the height of the larger container. Since all sides of the larger container have the same length, the height of the larger container is 7 inches.
Therefore, the water will be approximately 7 inches deep in the larger container.
For more such questions on container
https://brainly.com/question/29398973
#SPJ8
i would appreciate help,i dont need an explanation, just the answers. thankyou

Answers
we have
f(x)=7x-1
g(x)=(1/7)(x+1)
Part 1
Find out (fog)(x)
(fog)(x)=f(g(x))=7(1/7)(x+1)-1=x+1-1=x
therefore
(fog)(x)=x
Part 2
Find out (gof)(x)
(gof)(x)=g(f(x))=(1/7)(7x-1+1)=x
therefore
(gof)(x)=x
Part 3
(fog)(x)=(gof)(x)=x
the answer is Yes
( Which of the following best describes an ecosystem in a neighborhood garden?
Answers
what is 9x187647x27489x638927
Answers
Answer:
2.9661582
Step-by-step explanation:
2.9661582e+16 this is the answer
The hotdog stand at a baseball game sells hotdogs for $3.50 each. The amount, D dollars, Mr. Moore paid for the hotdogs is directly proportional to the number of hotdogs, H, he buys. Identify the constant of proportionality and write a direc
Answers
Answer:
D α H
k = D/H
k = 3.50
Step-by-step explanation:
Amount paid, D is directly proportional to the number of hotdogs, H
D = $3.50 per hot dog
D = $3.50 is directly proportional to 1 hotdog
Hence,
D α H
D = kH
k = proportionality constant
H = 1
3.50 = k
k = 3.50
k = D/H
After obtaining two heads from two tosses of a coin, the probability of obtaining a head on the next toss is a 1/2 b 3/8 c 1/4 d 1/8
Answers
Answer:
The correct option is a) 1/2
The probability of obtaining a head after obtaining two heads from two tosses of a coin is 1/2.
What is probability?
Probability is a branch of mathematics concerned with the study of random events or occurrences.
Probability is a quantitative measure of the likelihood that a given event will occur.
Probability is usually given as a number between zero and one (0 ≤ P(E) ≤ 1), where,
P(E) = 0, the event is considered impossible, and
when P(E) = 1, the event is considered a certainty.
What is the probability of obtaining a head after obtaining two heads from two tosses of a coin?
After obtaining two heads from two tosses of a coin, the probability of obtaining a head on the next toss is given by:
Sample space, S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}where H is for head and T is for tail.
Therefore, the probability of obtaining a head after obtaining two heads from two tosses of a coin is given by:
P(E) = favorable outcomes/total outcomes
The favorable outcome in this case is {HHH, HHT, HTH, THH, TTH}.
Hence, P(E) = 5/10
= 1/2
Therefore, the correct option is a) 1/2.
Learn more about probability, visit here
https://brainly.com/question/13604758
#SPJ11
A department store paint mixer contains 4 pints of equal amounts of yellow and red paint. The shade of red that you want requires a paint mixture that is 75% red and 25% yellow. How many pints of red paint need to be added to the paint mixer?
Answers
2.67 pints of red paint to be added to the paint Mixer in order to achieve the desired 75% red and 25% yellow mixture.
The number of pints of red paint that need to be added to the paint mixer, we need to calculate the amount of paint in the mixer currently and find the difference between that amount and the desired 75% red mixture.
Currently, the paint mixer contains 4 pints of equal amounts of yellow and red paint. Since the yellow and red paint are in equal amounts, we can say that there are 2 pints of red paint in the mixer.
Now, let's calculate the amount of red paint required for the desired mixture. We want the final mixture to be 75% red, which means that 75% of the total mixture should be red.
the total mixture required is X pints. Since 75% of the mixture should be red, we have:
0.75X pints of red paint.
Since the current amount of red paint in the mixer is 2 pints, we can subtract this from the desired amount to find the additional pints of red paint needed:
0.75X - 2 pints.
We want the additional pints of red paint to equal 0, so we set up the equation:
0.75X - 2 = 0.
Solving this equation, we find:
0.75X = 2.
X = 2 / 0.75.
X ≈ 2.67.
Therefore, we need approximately 2.67 pints of red paint to be added to the paint mixer in order to achieve the desired 75% red and 25% yellow mixture.
For more questions on Mixer .
https://brainly.com/question/20532904
#SPJ8
How much greater is 3000 then 1?
Answers
2999 greater than 1
In the last 6 days, Laura has
jogged 39 miles. At what rate did
Laura jog each day?
A: 234 miles per day
B: 33 miles per day
C: 6.5 miles per day
D: 0.15 miles per day
Answers
Answer:
6.5 miles per day
Step-by-step explanation:
Take the number of miles and divide by the number of days
39 miles/ 6 days
6.5 miles per day
Answer: 6.5 miles per day is correct
Step-by-step explanation:
You would just need to divide 39 by 6 to find the total miles per day. Therefore C: 6.5 is correct!
suppose a triangle has two sides of length 2 and 5 and that the angle between these two sides is 60 degrees. whart is the length of the third side of the triangle
Answers
Answer:
Step-by-step explanation:
Using Law of Cosine
Suppose Angle A is 60 degrees which is between sides b and c.
we need to find the length of side a
a^2 = b^ + c^ - 2bcCos60
a^2 = 4 + 25 - 20Cos60
a^2 = 29 - 20Cos60
a = 4.3588
Step-by-step explanation:
the other answer is correct but missed a few steps in the explanation. so, just to be sure :
yes, we use the law of cosine (or I call it the general Pythagoras for non-right-angled triangles) :
c is the side opposite of the given angle. a, b are the other 2 sides.
c² = a² + b² - 2ab×cos(angle)
in our case
c² = 2² + 5² - 2×2×5×cos(60°) =
= 4 + 25 - 20×0.5 = 29 - 10 = 19
c (the third side) = sqrt(19) = 4.358898944... units
you see how this is connected to the regular Pythagoras in right-angled triangles ?
c² = a² + b² - 2ab×cos(90°)
cos(90°) = 0
and so all that is left is
c² = a² + b²
What multiplied by 15 equals 750?
Answers
Answer:
50
Step-by-step explanation:
3.5 + 1.2(6.3 – 7x) = 9.38
Answers
Answer: 0.2
Step-by-step explanation:
subtract 9.38 - 3.5 = 5.88
distribute the 1.2.
7.56 - 8.4x = 5.88
subtract 5.88 - 7.56 = -1.68
-8.4x = -1.68
divide both sides by -8.4
answer = 0.2