ANSWER ASAP IM TIMED WILL MARK BRAINLIEST!!
Complete the following questions.
1. It costs Bill $35.50 to make a 3 tier chocolate cake. He marks his cakes up by 60%, what is the markup? What is the selling price of the cake?
2. Sue has $14.75 in making a flower arrangement. She marks them up by 45%. What is the markup? What is the selling price?
3. Jim goes to Walmart and purchases items that costs $98.25. The sales tax rate is 7%. How much tax does he pay? How much is his total?
4. Jill purchases a car for $19,250.95. The sales tax rate is 4.5%. How much sales tax does she pay? How much is the total cost of the car?
Answers
1. 35.50 increase 60% =
35.50 × (1 + 60%) = 35.50 × (1 + 0.6) = $56.80
2. 14.75 increase 45% =
14.75 × (1 + 45%) = 14.75 × (1 + 0.45) = 21.3875 = $21.39
3. 98.25 increase 7% =
98.25 × (1 + 7%) = 98.25 × (1 + 0.07) = 105.1275 = $105.13
4. 19250.95 increase 4.5% =
19250.95 × (1 + 4.5%) = 19250.95 × (1 + 0.045) = 20117.24275 = $20117.24
Related Questions
Pls need help thank you
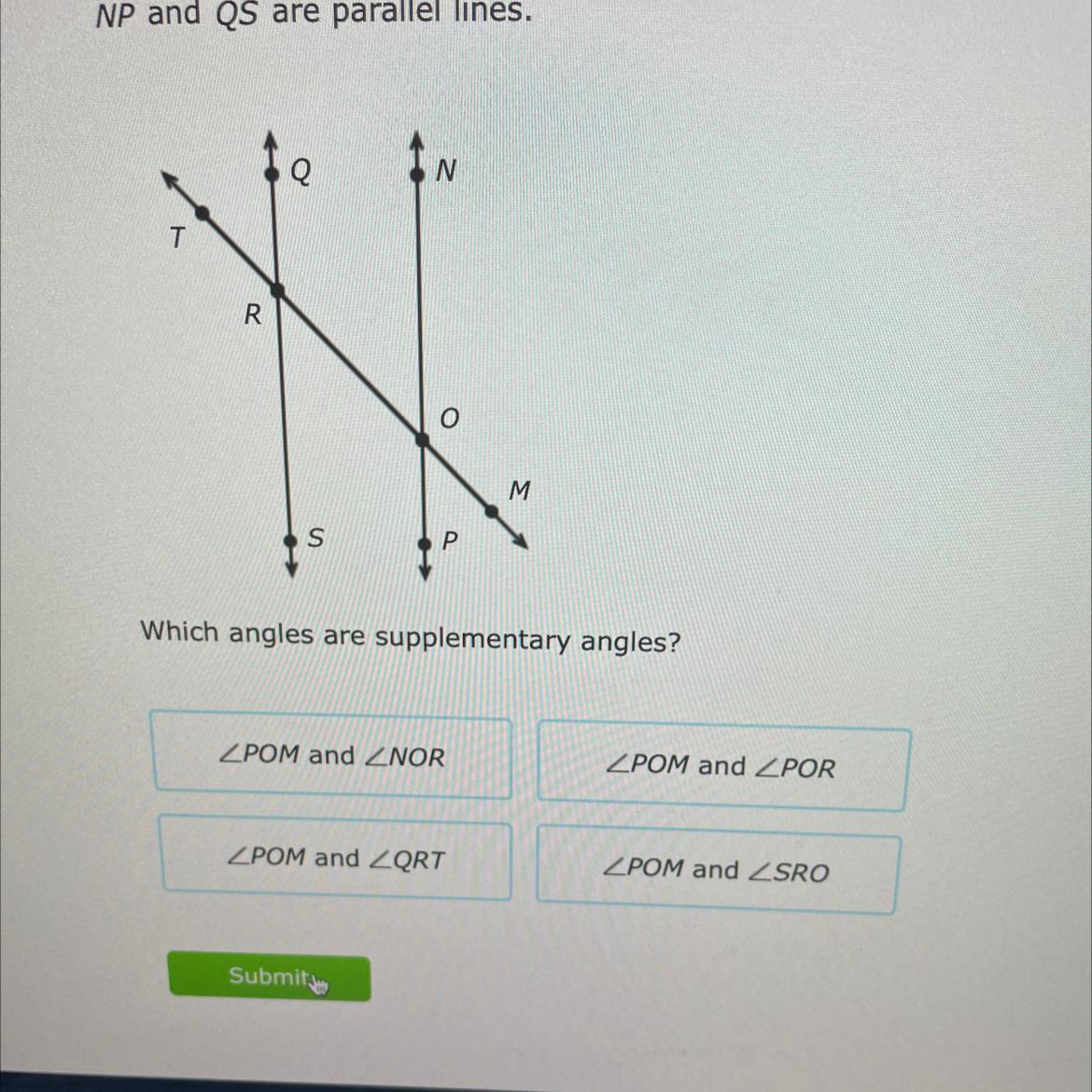
Answers
Answer:
∠POM and ∠POR
Step-by-step explanation:
Step-by-step explanation:
angle POM and angle QRT
3 values that would make this inequality true. 65 < 15x
Answers
Answer:
x>13/3
Step-by-step explanation:
solve this y = x + 4 for x.
Answers
Answer:
Nothing further can be done.
Step-by-step explanation:
To produce at a point lying ______ the production possibilities curve would require economic growth.
Answers
To produce at a point lying inside the production possibilities curve would require economic growth.
What is production possibilities curve ?The production possibilities curve can be described as a graph that help to display the different combinations of output which can be gotten from given current resources and technology.
In this case, To produce at a point lying inside the production possibilities curve would require economic growth.
Learn more about production possibilities curve on:
https://brainly.com/question/26460726
#SPJ4
Four rats are selected at random from a cage of 5 male (M) and 6 female (F) rats. If the random variable Y is concerned with the number of female rats taken out of the cage, construct the probability distribution and answer the questions below. (input up to 4 decimal places)A What is the probability that all selected rats are female?
What is the probability that only one of the selected rats is female?
c. What is the probability that at least two of the selected rats is female?
What is the mean of the probability distribution?
E. What is the standard deviation of the probability distribution?
Answers
Using the hypergeometric distribution, it is found that the distribution is:
P(X = 0) = 0.0152
P(X = 1) = 0.1818
P(X = 2) = 0.4545
P(X = 3) = 0.3030
P(X = 4) = 0.0455
Hence:
A) There is a 0.0455 = 4.55% probability that all selected rats are female.
B) There is a 0.1818 = 18.18% probability that only one of the selected rats is female.
C) There is a 0.803 = 80.3% probability that at least two of the selected rats is female.
D) The mean of the probability distribution is of 2.18.
E) The standard deviation of the probability distribution is of 0.833.
The rats are chosen without replacement, hence the hypergeometric distribution is used to solve this question.
What is the hypergeometric distribution formula?The formula is:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}C_{N-k,n-x}}{C_{N,n}}\)
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
The parameters are:
x is the number of successes.N is the size of the population.n is the size of the sample.k is the total number of desired outcomes.In this problem:
There is a total of 11 rats, hence N = 11.6 of the rats are female, hence k = 6.4 rats are taken, hence n = 4.The distribution is the probability of each outcome, hence:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}C_{N-k,n-x}}{C_{N,n}}\)
\(P(X = 0) = h(0,11,4,6) = \frac{C_{6,0}C_{5,4}}{C_{11,4}} = 0.0152\)
\(P(X = 1) = h(1,11,4,6) = \frac{C_{6,1}C_{5,3}}{C_{11,4}} = 0.1818\)
\(P(X = 2) = h(2,11,4,6) = \frac{C_{6,2}C_{5,2}}{C_{11,4}} = 0.4545\)
\(P(X = 3) = h(3,11,4,6) = \frac{C_{6,3}C_{5,1}}{C_{11,4}} = 0.3030\)
\(P(X = 4) = h(4,11,4,6) = \frac{C_{6,4}C_{5,0}}{C_{11,4}} = 0.0455\)
Item a:
P(X = 4) = 0.0455, hence:
There is a 0.0455 = 4.55% probability that all selected rats are female.
Item b:
P(X = 1) = 0.1818, hence:
There is a 0.1818 = 18.18% probability that only one of the selected rats is female.
Item c:
\(P(X \geq 2) = P(X = 2) + P(X = 3) + P(X = 4) = 0.4545 + 0.3030 + 0.0455 = 0.803\)
There is a 0.803 = 80.3% probability that at least two of the selected rats is female.
Item d:
The mean of the hypergeometric distribution is:
\(\mu = \frac{nk}{N}\)
Hence:
\(\mu = \frac{4(6)}{11} = 2.18\)
The mean of the probability distribution is of 2.18.
Item e:
The standard deviation of the hypergeometric distribution is:
\(\sigma = \sqrt{\frac{nk(N-k)(N-n)}{N^2(N-1)}}\)
Hence:
\(\sigma = \sqrt{\frac{4(6)(11-6)(11-4)}{11^2(11-1)}} = 0.833\)
The standard deviation of the probability distribution is of 0.833.
More can be learned about the hypergeometric distribution at https://brainly.com/question/24826394
how many 6-word sentences can be made using each of the 26 letters of the alphabet exactly once?
Answers
The number of 6-word sentences is 559902673349120609600000.
There are a total of 26! (26 factorial) possible 6-word sentences that can be made using each of the 26 letters of the alphabet exactly once.
This is because there are 26 options for the first letter, 25 options for the second letter, 24 options for the third letter, and so on until there is only one option left for the last letter.
Therefore, the total number of possible 6-word sentences is 26! = 26 * 25 * 24 * 23 * 22 * 21 * 20 * 19 * 18 * 17 * 16 * 15 * 14 * 13 * 12 * 11 * 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 403291461126605635584000000.
To calculate the number of 6-word sentences, we need to divide the total number of possible sentences by the number of possible arrangements of 6 words.
This is because each 6-word sentence can be arranged in 6! (6 factorial) different ways. Therefore, the number of 6-word sentences is 26! / 6! = 403291461126605635584000000 / 720 = 559902673349120609600000.
For more similar questions on sentence:
brainly.com/question/552895
#SPJ11
Function graphing
Sketch a graph of the function f(x) = - 5 sin 6 5 4 3 2 -&t -7n -65-4n -3n-2n - j -2 -3 -4 -5 -6 + - (a) 27 3 4 5 \ / 67 8
Answers
To sketch the graph of the function `f(x) = - 5 sin 6 5 4 3 2 -&t -7n -65-4n -3n-2n - j -2 -3 -4 -5 -6 + - (a) 27 3 4 5 \ / 67 8`, we first need to identify its key features, which are:Amplitude = 5
Period = 2π/6
= π/3
Phase Shift = 2
The graph of the function `f(x) = - 5 sin 6x + 2` can be obtained by starting with the standard sine graph and making the following transformations:Reflecting it about the x-axis by multiplying the entire function by -1.
Multiplying the entire function by 5 to increase the amplitude.
Shifting the graph to the right by 2 units.For the specific domain provided in the question, we have:27 < 6x + 2 < 67 or 25/6 < x < 65/6.
This gives us a range of approximately 4.17 ≤ x ≤ 10.83.
To know more about graph visit :-
https://brainly.com/question/19040584
#SPJ11
What are the zeros of the function h (x) = x² + 3x - 8?
A
x = -8 and x = -2
OB
x= -8 and x = 2
cx = -2 and x = 8
OD x = 2 and x = 8

Answers
The following are the zeros for the function h (x) = x2 + 3x - 8: - x= -4 and x=2.
Describe functions.Given a collection of inputs X (domain) and a set of potential outputs Y (codomain), a function is more technically defined as a set of ordered pairings (x,y) where xX and yY with the caveat that there can only be one ordered pair with the same value of x. The function notation f:XY can be used to express that f is a function from X to Y.
The function's zero is a value of x that makes it equal to zero. In other words, the equation f(x) = 0 leads to a zero.
By putting h(x) equal to zero and figuring out x, we may determine the zeroes for the function h(x) = x2 + 3x - 8.
h(x) = x² + 3x - 8 = 0
We may factor the left side of the equation to find x:
x² + 3x - 8 = (x-2)(x+4) = 0
We set each factor to zero and solve for x to discover the zeroes:
x-2 = 0 or x+4 = 0
x = 2 or x = -4
Consequently, the function's zeros are x = 2 and x = -4.
So, A is the right response. x = -4 and x = 2
To know more about functions visit:
https://brainly.com/question/29120892
#SPJ1
The complete question is
What are the zeros of the function h (x) = x² + 3x - 8?
A. x = -4 and x = -2
B. x= -8 and x = 2
C. x = -2 and x = 8
D. x = 2 and x = 8
Graph the following function by hand by completing the table
g(x) = (x - 5)² – 3

Answers
We know that y - x^2 is a parabola with a vertex at (0, 0).
So if we move it 5 units to the right and 3 units down, the vertex is at (5, -3).
Since it gives you a chart, you can plug in values for x and solve for g(x), and you will eventually get a graph that looks like a parabola with vertex at (5, -3).
A continuous random variable X has probability density function f(x) = c(1+x)(1 - 2 over the domain -1<<1. (a) i. Evaluate the constant e (the integration can be done by MATLAB). ii. Plot the probability density function over the domain (-1,1). Is this density function skewed to the right, skewed to the left, or symmetric? (b) Use MATLAB to evaluate I i. the mean y = E(X)= |- «f(x) dx; ii. E(X)= (- 22 f(x) dx; iii. the variance o2 = Var(X) = E(X) – H?, and the standard deviation o. *(c) i. Use MATLAB to find an expression for the cumulative distribution function F(x). ii. Check the result in (i) by differentiation. Hint: simplify (ans) might help! iii. Evaluate P(-0.2 X <0.2).
Answers
(a)i. Evaluating the constant:
\($$\int_{-1}^{1} c(1+x)(1-2x) dx = 1$$$$\implies c = \frac{3}{4}$$\)
Therefore, the probability density function is:
\($$f(x) = \frac{3}{4} (1+x)(1-2x), -1< x < 1$$\) ii. Plotting the probability density function:
From the graph, it is observed that the density function is skewed to the left.
(b)i. The mean:
\($$E(X) = \int_{-1}^{1} x f(x) dx$$$$E(X) = \int_{-1}^{1} x \frac{3}{4} (1+x)(1-2x) dx$$$$E(X) = 0$$\)
ii. The second moment about the origin:
\($$E(X^2) = \int_{-1}^{1} x^2 f(x) dx$$$$E(X^2) = \int_{-1}^{1} x^2 \frac{3}{4} (1+x)(1-2x) dx$$$$E(X^2) = \frac{1}{5}$$\)
Therefore, the variance is:
\($$\sigma^2 = E(X^2) - E(X)^2$$$$\implies \sigma^2 = \frac{1}{5}$$\)
iii. The standard deviation:
$$\sigma = \sqrt{\sigma^2} = \sqrt{\frac{1}{5}} = \frac{\sqrt{5}}{5}$$(c)
i. The cumulative distribution function:
\($$F(x) = \int_{-1}^{x} f(t) dt$$$$F(x) = \int_{-1}^{x} \frac{3}{4} (1+t)(1-2t) dt$$\)
ii. The probability density function can be obtained by differentiating the cumulative distribution function:
\($$f(x) = F'(x) = \frac{3}{4} (1+x)(1-2x)$$\)
iii. Evaluating\(P(-0.2 < X <0.2):$$P(-0.2 < X <0.2) = F(0.2) - F(-0.2)$$$$P(-0.2 < X <0.2) = \int_{-0.2}^{0.2} f(x) dx$$$$P(-0.2 < X <0.2) = \int_{-0.2}^{0.2} \frac{3}{4} (1+x)(1-2x) dx$$$$P(-0.2 < X <0.2) = 0.0576$$\)
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
I read 1/3 of a book in an hour.
How much more of the book will I read in 2 1/5 hours
Answers
Answer:
Step-by-step explanation:
To find the number of pages of the book in the given hour:
To find the number of pages in 2 1/5 hours, multiply the number of pages read in 1 hour by 2 1/5 hours.
\(\sf \text{ Number of pages read in 2 $\dfrac{1}{5}$ hours = $\dfrac{1}{3}*2\dfrac{1}{5}$ }\)
\(\sf = \dfrac{1}{3}*\dfrac{11}{5}\\\\=\dfrac{11}{15}\)
\(\sf \text{Number of pages read more in 2 $\dfrac{1}{5}$ hours = $\dfrac{11}{15}-\dfrac{1}{3}$}\)
\(\sf =\dfrac{11}{15}-\dfrac{1*5}{3*5}\\\\=\dfrac{11}{15}-\dfrac{5}{15}\\\\=\dfrac{6}{15}\)
Answer:
see below
Step-by-step explanation:
Here is another way
1/3 book / hr * 2 1/5 hr =
1/3 * 11/5 = 11/15 read in 2 1/5 hr
1/3is the same as 5 /15
11/15 - 5 /15 = 6/15 = 2/5 more read in 2 1/5 hr that 1/3 hr
consider two random variables x and y with joint pmf given by pxy(k,l)=12k l,for k,l=1,2,3,... show that x and y are independent and find the marginal pmfs of x and y. find p(x2 y2≤10)
Answers
Answer:
Step-by-step explanation:
To show that X and Y are independent, we need to check that their joint PMF factorizes into the product of their marginal PMFs, i.e., PXY(k,l) = PX(k)PY(l) for all k,l.
To do this, we need to find the marginal PMFs of X and Y. We can do this by summing over all possible values of the other variable, as follows:
PX(k) = ∑l=1,2,3,... PXY(k,l) = ∑l=1,2,3,... 1/(2^(k+l))
At grocery mart,apples are on sale 6 apples for $3.54. find the unit cost?
Answers
Answer:
$.59 per apple
Step-by-step explanation:
The unit cost is the price divided by the number of items
3.54 / 6
.59
$.59 per apple
Answer:
0.59 or .59
Step-by-step explanation:
3.54 divided by 6
From the given figure,write the corresponding angle of puv

Answers
Answer: RVN
Step-by-step explanation:
Corresponding angles are angles which occupy the same relative position at each intersection where a straight line crosses two others. If the two lines are parallel, the corresponding angles are equal.
By that - the bottom angle RVN can be an example of corresponding angles.
Please give brainliest!
Answer:
∠ RVN
Step-by-step explanation:
∠ PUV and ∠ RVN are corresponding angles.
Each is in the same position (lower left hand corner ) in its group of 4 angles.
Solve the following equation in the picture....thanks:)

Answers
The Verdicts on each value of u according to the given inequality are as follows; 11, 13 and 8.
What values ares solutions to the inequality; u ≤ 13?It follows from the task content that the values which are solutions to the inequality; u ≤ 13 are to identified.
To determine the solution of an inequality on a number line, the number line representation of such inequality is very pivotal.
Therefore, the inequality given; u ≤ 13 simply implies that; the solution set of u includes 13 and all numbers to the left of 13 on the number line.
Hence, by considering each of the given values of u; we have;
11 ≤ 13?; Yes.13 ≤ 13?; Yes.8 ≤ 13?; Yes.18 ≤ 13?; No.Ultimately, the solutions to the inequality among the answer choices are; 11, 13 and 8 respectively.
Read more inequality solutions;
https://brainly.com/question/24372553
#SPJ1
Find the number of 4 digit numbers that contain at least 3 even digits
Answers
Answer:
2625 different numbers
Step-by-step explanation:
General outlineCombinatoricsSpecial circumstancesPartitioning the situationConclusionPart 1. CombinatoricsThis type of problem is classified as a "Combinatorics" problem: Counting up the number of ways something can happen.
Many times when attempting to count a large number of items, patterns are recognized and shortcuts to count are developed so that one doesn't need to physically count all of the items. Perhaps the trickiest part of counting with these shortcuts is to ensure that one does not over-count (counting a scenario more than once), although it is equally important that we don't under-count (fail to count a situation that applies).
Part 2. Special circumstancesIt should be noted that for a number to be a 4 digit number, it must have 4 digits, and thus the first digit must not be zero (despite that that would be an even digit, the number itself would not be a 4 digit number).
Part 3. Partitioning the situationThere are 2 main scenarios:
1. All 4 digits are even
2. Exactly 3 digits are even (meaning that exactly one digit is odd).
There are two sub-cases to Scenario 2:
2.1. The first digit is odd, and all three of the other digits are even.
2.2. The first digit is even, and exactly two of the other digits are even (meaning that exactly one of the last three digits is odd).
None of scenarios 1, 2.1, and 2.2 overlap, so we're not over-counting:
If all 4 digits are even, then there can't be exactly 3 even digits. If the first digit is odd, then not all 4 digits are even nor is the first digit even. If exactly two of the last three digits are even, then not all 4 digits are even, nor are all three of the last digits even.Further, this is all of the possibilities for a 4 digit number with least three even digits, so we're not under-counting.
Scenario 1 -- All 4 digits are even.
If all 4 digits are even, then the first digit has fours choices (2,4,6,8), and the next 3 digits each have 5 choices (2,4,6,8,0).
\(4*5*5*5=500\text{ choices}\)
Scenario 2.1 -- The first digit is odd, and all three of the other digits are even
If the first digit is odd, there are 5 choices for the first digit (1,3,5,7,9), and the next 3 digits each have 5 choices (2,4,6,8,0).
\(5*5*5*5=625\text{ choices}\)
Scenario 2.2 -- The first digit is even, and exactly two of the other digits are even
If the first digit is even, there are 4 choices for the first digit (2,4,6,8), and if exactly two of the next 3 digits are even, then there are 5 choices for each of the two even digits (2,4,6,8,0), and 5 choices for the odd digit (1,3,5,7,9), and there are "3 permuted by 2" ways of ordering those three digits.
\(4* \left [(5*5*5) * {}_3 \! P_2 \right ]=\\\\=4*\left [5*5*5 * \dfrac{3!}{2!} \right ]\\\\=4*\left [ 5*5*5 * \dfrac{3*2*1}{2*1} \right ] \\\\=4*\left [5*5*5 * 3 \right ] \\\\=1500\text{ choices}\)
Scenario 2.2 broken down (calculated without using the permutation operation) -- The first digit is even, and exactly two of the other digits are even
Then either the second digit is odd (scenario 2.2.1), the third digit is odd (scenario 2.2.2), or the fourth digit is odd (scenario 2.2.3).
Scenario 2.2.1. The second digit is odd.
The first digit is even: 4 choices for the first digit (2,4,6,8)
The second digit is odd: 5 choices for the odd digit (1,3,5,7,9)
The third and fourth digits are even: 5 choices for each even digit (2,4,6,8,0).
\(4*5*5*5=500\text{ choices}\)
Scenario 2.2.2. The third digit is odd.
The first digit is even: 4 choices for the first digit (2,4,6,8)
The second and fourth digits are even: 5 choices for each even digit (2,4,6,8,0).
The third digit is odd: 5 choices for the odd digit (1,3,5,7,9)
\(4*5*5*5=500\text{ choices}\)
Scenario 2.2.3. The last digit is odd.
The first digit is even: 4 choices for the first digit (2,4,6,8)
The second and third digits are even: 5 choices for each even digit (2,4,6,8,0).
The last digit is odd: 5 choices for the odd digit (1,3,5,7,9)
\(4*5*5*5=500\text{ choices}\)
Scenarios 2.2.1, 2.2.2, and 2.2.3 comprise all of Scenario 2.2, so \(500+500+500=1500\text{ choices}\)
Part 4. ConclusionHow many ways can a 4 digit number be formed where at least 4 of the digits are even?
This is the sum of the choices from Scenario 1, Scenario 2.1, and Scenario 2.2, so \(500+625+1500=2625\text{ choices}\).
PLS HELP ME
XXXXXXXXX

Answers
Answer:
1
Step-by-step explanation:
To find the median number of musical instruments played, we first need to arrange the data in ascending order:
0, 0, 0, 0, 1, 1, 2, 2, 3, 3, 3
Next, we count the total number of responses, which is 15. Since 15 is an odd number, the median will be the average of the middle value.
The middle value is 1
Hence, the median number of musical instruments played is 1.
PLEASE HELP DUE IN 30 MINUTES FIND ? AND SHOW YOUR WORK

Answers
Answer:
?= 180-(75+39)=66
Step-by-step explanation:
......
Answer:
66
Step-by-step explanation:
A triangle's angles always add up to 180.
So to find the missing angle, subtract the angles we already have by 180.
180-(75+39) = ?
180-114 = 66
I hope this helps!
Can someone please give me the (Answers) to this? ... please ...
I need help….

Answers
Since these two triangles are similar, that means all their side lengths are proportional:
\(\frac{SR}{ST} =\frac{CB}{CD} \\\frac{11x-4}{70} =\frac{60}{50} \\550x-200=4200\\550x = 4400\\x = 8\\\)
Hope that helped!
5n>7n+24 How do you solve it?
Answers
\(Answer:\)
\(n < - 12\)
\(Step-by-step explanation:\)
~\(Subtract\) \(7n\) \(from\) \(both\) \(sides\)
~\(Simplify\)
~\(Multiply\) \(both\) \(sides\) \(by\) \(-1\) {reverse the inequality}
~\(Simplify\)
~\(Divide\) \(both\) \(sides\) \(by\) \(2\)
⇒\(n < - 12\)
An automobile uses 17 gal of fuel to go 590 mi. how many gallons are required to travel 840 mi? (round your answer to one decimal place.)
Answers
Answer:
the car would use 49 gallons because you get a decimal of 49.49 so you would put got decimal to the nearest 1's place and that would be 49
find the absolute maximum and absolute minimum (if any) of the given function on the specified interval. f (x)
Answers
The answer of the function found to be x = −4 and x = 2, with M = 38.
We must consider the function,
f (x) = x³ + 6x² + 6
Over the interval
-5 \(\leq\) x \(\leq\) 2
To obtain the extrema we start from the function's derivative.
f' (x) = 3x² + 12x
Equating it to 0,
f' (x) = 0 = 3x(x +4) = 0
We arrive at two solutions,
x1 = 0, x2 = -4 both inside the interval.
Evaluating the function at the stationary points,
f (x1) = 6
f (x2) = (-4)³ + 6 . (-4)² + 6 = -64 + 96 + 6 = 38
These values must be compared to that of the function at the interval frontiers,
f (-5) = (-5)³ + 6 . (-5)² + 6 = -125 + 150 + 6 = 31
f (2) = 2³ + 6 . 2² + 6 = 38
Comparing the results we can conclude that the function attains its absolute minimum at,
x = 0, m = 6
Meanwhile, the absolute maximum is attained at the points,
x = −4 and x = 2, with M = 38.
Learm more about maxima and minima here; https://brainly.com/question/82347
#SPJ4
The Rectangle is 212units x 212units Area
Answers
The rectangle has equal dimensions, and the area of the rectangle is 44944 square units
How to detemine the area?The given parameters are:
Length = 212 units
Width = 212 units
The area of the rectangle is:
Area = Length * Width
So, we have:
Area = 212 * 212
Evaluate
Area = 44944
Hence, the area of the rectangle is 44944 square units
Read more about area at:
https://brainly.com/question/24487155
#SPJ1
6sin^2 (x) + 6sin (x) + 1 = 0
solve and show steps for the graph ( i already have the graph )
Answers
To solve the equation \(6sin^2(x)\) + 6sin(x) + 1 = 0, we can use algebraic methods and the unit circle to determine the values of x that satisfy the equation.
1. Start by rearranging the equation to a quadratic form: \(6sin^2(x)\) + 6sin(x) + 1 = 0.
2. Notice that the equation resembles a quadratic equation in terms of sin(x). Let's substitute sin(x) with a variable, such as u: \(6u^2\) + 6u + 1 = 0.
3. Solve this quadratic equation for u. You can use the quadratic formula or factorization methods to find the values of u. The solutions are u = (-3 ± √3) / 6.
4. Since sin(x) = u, substitute back the values of u into sin(x) to obtain the values for sin(x): sin(x) = (-3 ± √3) / 6.
5. To find the values of x, we can use the inverse sine function. Take the inverse sine of both sides: x = arcsin[(-3 ± √3) / 6].
6. The arcsin function has a range of [-π/2, π/2], so the values of x lie within that range. Use a calculator to find the approximate values of x based on the values obtained in step 5.
7. Plot the obtained x-values on the graph to show the solutions of the equation \(6sin^2(x)\) + 6sin(x) + 1 = 0. The graph will illustrate the points where the curve intersects the x-axis.
For more such questions on algebraic, click on:
https://brainly.com/question/4344214
#SPJ8
Based on the passage, what is the best inference?
-John doesn’t want to see the show.
-John is happy about being given the ticket.
-John has trouble making decisions.
-John often makes decisions too quickly.
"I don't know what to do," John sighed and shrugged as he stared at the free ticket for tomorrow's show that he'd just been given. "I planned to go to the beach tomorrow."
Answers
Answer:
John has trouble making decisions.
Step-by-step explanation:
In the passage, it says the "I don't know what to do," John sighed and shrugged as he stared at the free ticket for tomorrow's show that he'd just been given. ,¨ indicates he´s having some trouble.
Answer:
John has trouble making decisions < 3
...................................................................................................................................
This is 100 % correct :'}
.................................................................................................................................
I know im late lol , but for the people who didnt know what the answer was this is the answer ! ;')
....................................................................................................................................
Have a nice day < 33 !
...................................................................................................................................
A 6-foot diameter circle is divided
into six congruent sectors. What
is the area of each sector in square
inches? (Use 3.14 for 2.)
Answers
Answer:
the area is 1235
Step-by-step explanation:
Answer:
2714.33 sq in
explanation-
since circle is divided into 6 congruent sectors, area of each sector is 1/6th of area of circle.\(ar \: of \: sector \: = ar \: of \: circle \: \div 6 \\ = \pi \times 72 \times 72 \div 6 \\ = 2714.33\)Can someone help me answer this question??? LOL :)

Answers
For the exponential function:
g(x) = 14*(2)^x
We can see that:
a = 14, and b = 2.
How to identify the parts of the exponential function?A general exponential function is written as:
y = a*(b)^x
Where a is the inital value of the exponential function and b is the base.
Here we have the exponential function:
g(x) = 14*(2)^x
Comparing that to the general one, we can see that the initial value is 14 and the base is 2.
Then:
a = 14
b = 2
The correct option is the second one.
Learn more about exponential functions at.
https://brainly.com/question/11464095
#SPJ1
what is the equation of a line that is perpendicular to the line y=2x+1 and passes through the point (4,6).
i need help asap! work shown to help me thru the steps. y=mx+b
Answers
keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above
\(y=\stackrel{\stackrel{m}{\downarrow }}{2}x+1\qquad \impliedby \qquad \begin{array}{|c|ll} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{2\implies \cfrac{2}{1}} ~\hfill \stackrel{reciprocal}{\cfrac{1}{2}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{1}{2}}}\)
so we're really looking for the equation of a line with a slope of -1/2 and that it passes through (4 , 6)
\((\stackrel{x_1}{4}~,~\stackrel{y_1}{6})\hspace{10em} \stackrel{slope}{m} ~=~ - \cfrac{1}{2} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{6}=\stackrel{m}{- \cfrac{1}{2}}(x-\stackrel{x_1}{4}) \\\\\\ y-6=- \cfrac{1}{2}x+2\implies {\Large \begin{array}{llll} y=- \cfrac{1}{2}x+8 \end{array}}\)
Suppose you roll a cube 30 times, what is a to describe the theoretical of rolling a 1, 4, 6, 7 Please help me!
Answers
Answer:
\(Pr(x) = \frac{1}{6}\)
Step-by-step explanation:
Given
\(n = 30\) --- number of rolls
Required
The theoretical probability of rolling: (a) 1 (b) 4 (c) 6 (d) 7
Assume the cube is 6 sided.
The sample space is:
\(S = \{1,2,3,4,5,6\}\)
And the probability of each is:
\(Pr(x) = \frac{1}{6}\)
Irrespective of the number of rolls, the theoretical probability of (a). (b), (c) and (d) is:
\(Pr(x) = \frac{1}{6}\)
the height of adult women in france is a normally distributed random variable with a mean of 64 inches and a standard deviation of 2.4 inches. find the probability that a randomly chosen women is less than 62 inches tall.
Answers
The probability that a randomly selected woman is less than 62 inches tall is approximately 20.23%.
To solve this problem, we need to standardize the height value of 62 inches using the mean and standard deviation given.
Allow X be the height of adult women in France. Then we've got:
X ~ N(64, 2.4)
To discover the probability that a randomly chosen woman is less than 62 inches tall, we need to discover P(X < 62).
Using the standard regular distribution components, we can standardize X as follows:
Z = (X - μ) / σ
Where μ is the imply and σ is the standard deviation of the regular distribution, and Z is a general regular random variable.
Substituting the given values, we get:
Z = (62 - 64) / 2.4 = -0.8333 (approx)
Now, we want to discover the chance P(Z < -0.8333) using the standard normal distribution table or a calculator.
Using a standard normal distribution table, we discover that
P(Z < -0.8333) is approximately 0.2023.
Therefore, the probability that a randomly selected woman is less than 62 inches tall is approximately 0.2023 or 20.23%.
Learn more about Standard Deviation:-
https://brainly.com/question/475676
#SPJ4