Annie bought a brand new car for $32,000. The car is now worth $21,000.
Answers
Related Questions
5.02×10^2 in standard form
Answers
Answer:
5020000000000.
Step-by-step explanation:
5.02×10^2 is in scientific notation so we must convert it to standard form getting that answer.
Please help!! 50 points!!
Use the exponential equation below to answer Part A, Part B, and Part C.
35^x = 8
Part A: Explain the steps to solve the equation.
Part B: Rewrite the exponential equation in logarithmic form using the definition of logarithms.
Part C: Use the equation from Part B to solve for x. Round to the nearest hundredth
Answers
Answer:
a) below
b) log_35 (8) = x
c) x = 0.58487
Step-by-step explanation:
a) 35^x=8
apply the exponent rule
xln(35) = ln(8) → x = ln(8)/ln(35) → x = 3ln(2)/ln(35)
x = 0.58487
c) log_35 (8) = x
x = log_35 (8)
base form (Rewrite 8 in power)
x = log_35 (2^3)
log rule: log_a(x^b) = b*log_a(x)
log_35 (2^3) = 3log_35(2)
x = 3log_35(2)
x = 0.58487
URGENTLY NEED HELP!!!!!!!!

Answers
Answer:
x = 31.3°
Step-by-step explanation:
\(cos (A) = \frac{b^{2} + c^{2} - a^{2} }{2bc} \)
here a = 8 , b = 11 , c = 15
using the formula:
cos(x) = (11² + 15² - 8²) / ( 2 * 11 * 15)
cos(x) = \(\frac{47}{55} \)
x = \(cos^{-1} (\frac{47}{55} )\)
x = 31.3°
find the derivatives of cos
Answers
Step by step solution is above

What is the slope of the line whose equation is y-45
y-4= (x-2)?

Answers
Answer:
5/2
Step-by-step explanation:
use formula
\(m = ( \frac{y2 - y1}{x2 - x1} )\)
\(m = ( \frac{4 - - 1}{2 - 0} )\)
\(m = ( \frac{5}{2} )\)
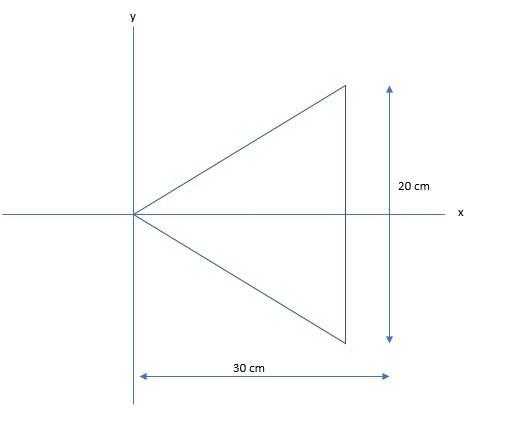
an 800 g steel plate has the shape of the isosceles triangle shown in the figure(figure 1).
Answers
The x- and y-coordinates of the center of mass are; (20, 0)
What is the center of mass of an object?The center of mass is the location where the sum of the relative position of the masses in a mass distribution is zero. It is the point where force can be applied on the distributed mass without causing a rotation of the system.
The mas of the steel plate = 800 g = 0.8 kg
The base length of the isosceles triangular plate = 20 cm = 0.2 m
The height of the isosceles triangular plate = 30 cm = 0.3 m
Considering a small strip of height, dx and width, I, we get
Area of small strip, dA = I·dx
Density of the plate for a unit thickness, ρ = M/A
Density of the small strip of mass dm = dm/dA
Considering the density of the plate as uniform, we get;
\(\displaystyle {\frac{dm}{dA} =\frac{M}{A}\)
Therefore;
\(\displaystyle {dm=\frac{M}{A}\times dA}\)
The area of the triangular plate, A = (1/2) × 0.2 m × 0.3 m = 0.03 m²
Mass of the plate, M = 0.8 kg
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx}\)
The width of the small strip, I, located at a distance x from the vertex of the triangular plate, using similar triangles, indicates;
\(\dfrac{I}{20} = \dfrac{x}{30}\)
\(I=20\times \dfrac{x}{30} = \dfrac{2}{3} \cdot x\)
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx} = \frac{0.8}{0.03}\times \dfrac{2}{3} \cdot x\cdot dx}\)
The center of mass, \(x_{cm}\), can be obtained with the formula; \(\displaystyle {x_{cm} = \dfrac{1}{M} \cdot \int\limits {x} \, dm }\)
Therefore; \(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx }\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx } = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0\)
\(\displaystyle {x_{cm} = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0=\frac{200}{9} \times \frac{0.027}{3} =0.2\)
The location of the x-coordinate center of mass, \(x_{cm}\) = 0.2 m = 20 cm from the vertex, which is the same location as the x-coordinate of the centroid of the plate of uniform density.
The plate is symmetrical about the x-axis, therefore, the y-coordinate of the center of mass is along the x-axis, which is \(y_{cm}\) = 0
The coordinate of the center of mass = (0.2, 0)
Part of the question requires the location of the coordinate of the center of mass of the triangular plate
Learn more about the center of mass of regular shapes here:
https://brainly.com/question/28021242
#SPJ1

Simplify the expression 4 + (-2)3. Three is to the third power
-12
12
-4
-2
Answers
If you take (-2) x 3 because of PEDMAS you’ll get -6
So -6 +4 is -2
Answer:
-2
Step-by-step explanation:
the national survey of student engagement found that 24% of seniors report that they often or very often went to class without completing readings or assignments.12 assume that the sample size of seniors is 276,000. (a) find the margin of error for 99% confidence.
Answers
Margin of error for 99% confidence interval is 0.0021
What is confidence interval?
he range of values that, should you repeat your experiment or resample the population in the same manner, you would anticipate your estimate to fall within a particular percentage of the time.
Main Body:
Given :
99% Confidence Interval for p
p = 0.24,n = 276000
Significance level = α = 1− confidence = 1 − 0.99 = 0.01
Critical z-value = zα/2 = z0.01/2 = z0.005 = 2.58 (closest value From z table)
Standard e
or of p : SE =
√p× (1 − p)n=√0.24 × 0.76276000
≈ 0.0008129
E = zα/2 ×√p× (1 − p)n
= 2.58 × 0.0008129 ≈ 0.002097
Hence ,Margin of Error or, E = 0.00210
To know more about confidence interval click on the link below
https://brainly.com/question/17097944
#SPJ4
Is 4.5 natural number?
Answers
Answer:
No
Step-by-step explanation:
4.5 IS NOT A WHOLE NUMBER!
Answer:
YES 4.5 IS NATURAL NUMBER
Step-by-step explanation:
Given slope = 1/4 & y- intercept = (0,-13) write the equation
Answers
Answer:
y=1/4x-13
Step-by-step explanation:
use y=mx+b where 0 is the x value, -13 is the y value, and 1/4 is the m value
-13=0+b
put back into y=mx+b where m is slope and b is y-intercept
Answer:
y=1/4x-13
Step-by-step explanation:
The question is wanting you to put the information in the format of y=mx+b. To create the equation you tie in the y-intercept which is -13 and the slope. You put the y-intercept in place of "b" and put the slope in place if the "m".
PLZ HELP!!!I’m having trouble

Answers
Answer:
41.41
Step-by-step explanation:
cosA=6/8=3/4
I used a calculator
How to convert 38 cm to inches?
Answers
Answer:14.9606
Step-by-step explanation:
38 cm = 14.9606 inches
How much is one centimeter in inches?
One inch is equivalent to 2.54 centimeters, and one centimeter is equal to 0.393701 inches, according to the conversion between the two units.
Exactly how big is one inch?
A yard and a foot are equivalent to an inch. A metric inch is precisely 2.54 centimeters. One whole inch is made up of two half inches and four quarter inches.
What is a inch ?
The British imperial and American customary systems of measurement both use the inch as their standard unit of length (symbolised as in or ′′).
What is a centimeter ?
The International System of Units' centimeter (SI symbol cm), sometimes known as a centimeter (international spelling) or centimeter (American spelling), is a unit of length (SI)
To know more about inches visit :
https://brainly.com/question/9264277
#SPJ4
Let f(n) and g(n) be asymptotically positive functions. Prove or disprove each of the following conjectures. f(n) = 0(g(n)) implies g(n) = O (f(n)). f(n) + g(n) = Theta (min(f(n), g(n))) f(n) = 0(g(n)) implies lg(f(n)) = O (lg(g(n))), where lg(g(n)) greaterthanorequalto 1 and f(n) greaterthanorequalto 1 for all sufficiently large n. f(n) = O (g(n)) implies 2 f^(n) = O (2^g(n)). f(n) = O ((f(n))2). f(n) = O (g(n)) implies g(n) = Ohm(f(n)) f(n) = Theta(f(n/2)). f(n) + o(f(n)) = Theta(f(n)).
Answers
The conjectures can be disproven with counterexamples.
Are the given conjectures supported by counterexamples?The first conjecture states that if f(n) = 0(g(n)), then g(n) = O(f(n)). However, this is not true in general. To disprove this, we can consider a counterexample where f(n) = n and g(n) = n^2. Here, f(n) is indeed O(g(n)), but g(n) is not O(f(n)), as g(n) grows faster than f(n).
The second conjecture suggests that if f(n) + g(n) = Theta(min(f(n), g(n))), then it holds true. However, this is not always the case. Counterexamples can be found by considering functions where f(n) and g(n) have different growth rates.
The third conjecture claims that if f(n) = 0(g(n)), then lg(f(n)) = O(lg(g(n))). However, this conjecture is also false. A counterexample can be constructed by taking f(n) = n and g(n) = n^2. While f(n) is indeed O(g(n)), lg(f(n)) is not O(lg(g(n))) as lg(g(n)) grows much faster than lg(f(n)).
The remaining conjectures can be similarly disproven with suitable counterexamples. It is important to note that disproving a conjecture requires finding just one counterexample that contradicts the statement.
Learn more about conjecture
brainly.com/question/11224568
#SPJ11
Which equation shows the relationship between the volume, (V) of the prism and its height (h)?

Answers
Answer:
h = V/lw
Step-by-step explanation:
We know the formula for the volume of a rectangular prism is V = lwh. We need to use this equation and solve for h by dividing lw on both sides.
V = lwh
V/lw = h
Find f(1), f(2), f(3), f(4) and f(5) if f(n) is defined recursively by f(0) = 3 and for n 0,1,2,....
Question a) f(n+1)=-2f(n)
Question b) f(n+1) = 3f(n)+7
Question c) f(n+1)=f(n)^2 -2f(n)-2
Question d) f(n+1) = 3^f(n)/3
Answers
The values for f(1), f(2), f(3), f(4), and f(5) using the recursive formula f(n+1) = 3^(f(n)/3) are:
f(1) = 3, f(2) = 3, f(3) = 3, f(4) = 3, f(5) = 3.
To find the values of f(1), f(2), f(3), f(4), and f(5) for each given recursive definition, we can use the initial condition f(0) = 3 and the recursive formulas.
(a) f(n+1) = -2f(n):
Using the recursive formula, we can find the values as follows:
f(1) = -2f(0) = -2(3) = -6
f(2) = -2f(1) = -2(-6) = 12
f(3) = -2f(2) = -2(12) = -24
f(4) = -2f(3) = -2(-24) = 48
f(5) = -2f(4) = -2(48) = -96
So, the values for f(1), f(2), f(3), f(4), and f(5) using the recursive formula f(n+1) = -2f(n) are:
f(1) = -6, f(2) = 12, f(3) = -24, f(4) = 48, f(5) = -96.
(b) f(n+1) = 3f(n) + 7:
Using the recursive formula, we can find the values as follows:
f(1) = 3f(0) + 7 = 3(3) + 7 = 16
f(2) = 3f(1) + 7 = 3(16) + 7 = 55
f(3) = 3f(2) + 7 = 3(55) + 7 = 172
f(4) = 3f(3) + 7 = 3(172) + 7 = 523
f(5) = 3f(4) + 7 = 3(523) + 7 = 1576
So, the values for f(1), f(2), f(3), f(4), and f(5) using the recursive formula f(n+1) = 3f(n) + 7 are:
f(1) = 16, f(2) = 55, f(3) = 172, f(4) = 523, f(5) = 1576.
(c) f(n+1) = f(n)^2 - 2f(n) - 2:
Using the recursive formula, we can find the values as follows:
f(1) = f(0)^2 - 2f(0) - 2 = 3^2 - 2(3) - 2 = 1
f(2) = f(1)^2 - 2f(1) - 2 = 1^2 - 2(1) - 2 = -3
f(3) = f(2)^2 - 2f(2) - 2 = (-3)^2 - 2(-3) - 2 = 7
f(4) = f(3)^2 - 2f(3) - 2 = 7^2 - 2(7) - 2 = 41
f(5) = f(4)^2 - 2f(4) - 2 = 41^2 - 2(41) - 2 = 1601
So, the values for f(1), f(2), f(3), f(4), and f(
using the recursive formula f(n+1) = f(n)^2 - 2f(n) - 2 are:
f(1) = 1, f(2) = -3, f(3) = 7, f(4) = 41, f(5) = 1601.
(d) f(n+1) = 3^(f(n)/3):
Using the recursive formula, we can find the values as follows:
f(1) = 3^(f(0)/3) = 3^(3/3) = 3^1 = 3
f(2) = 3^(f(1)/3) = 3^(3/3) = 3^1 = 3
f(3) = 3^(f(2)/3) = 3^(3/3) = 3^1 = 3
f(4) = 3^(f(3)/3) = 3^(3/3) = 3^1 = 3
f(5) = 3^(f(4)/3) = 3^(3/3) = 3^1 = 3
So, the values for f(1), f(2), f(3), f(4), and f(5) using the recursive formula f(n+1) = 3^(f(n)/3) are:
f(1) = 3, f(2) = 3, f(3) = 3, f(4) = 3, f(5) = 3.
Note: In the case of (d), the recursive formula leads to the same value for all values of n.
Learn more about recursive formula here:
https://brainly.com/question/1470853
#SPJ11
Q7-8 PLEASE HELP ME

Answers
Answer:
(-4,-7)
Step-by-step explanation:
Use the online graphing calculator called Desmos. That's what I did. Just input the two equations and it'll show you the completed graph. I hope this help you:)
reflection across y = -x
X(-4,-3), M(-3,-2), (-1,-5)
Answers
Reflection across the y = -x line is equivalent to a rotation of 180 degrees about the origin.
The coordinates of X(-4,-3) after reflecting across the y = -x line would be (3, 4)
The coordinates of M(-3,-2) after reflecting across the y = -x line would be (2, 3)
The coordinates of (-1,-5) after reflecting across the y = -x line would be (5,1)
So, after reflecting across the y = -x line, the coordinates of the points are flipped along the line x = y and they are moved to the opposite quadrant.
The exam scores (out of 100 points) for all students taking an introductory Statistics course are used to construct the following boxplot. Box plot About 25% of the students scores exceeded
Answers
About 75% of the students' scores exceeded the score mentioned in the boxplot.
In a boxplot, the box represents the interquartile range (IQR), which contains the middle 50% of the data. The lower whisker extends to the minimum value within 1.5 times the IQR below the first quartile (Q1), and the upper whisker extends to the maximum value within 1.5 times the IQR above the third quartile (Q3).
Since the boxplot does not provide specific numerical values, we can infer that the mentioned score lies within the upper whisker, which represents the top 25% of the data. Therefore, about 75% of the students' scores exceeded this score.
It's important to note that without the actual values or specific percentiles, we can only estimate the percentage based on the visual representation of the boxplot. The exact percentage may vary depending on the scale and distribution of the data. To obtain a more precise estimate, additional information such as the quartiles or a histogram of the scores would be needed.
To learn more about IQR, click here: brainly.com/question/21270410
#SPJ11
A messenger earns 2640 per year and pays tax at the rate of 10k On a naira how much tax does he pay in the year
Answers
Answer:
264 naira
Step-by-step explanation:
Given that:
Amount earned per year = 2460
Rate of interest paid : 10k per naira earned
Tax paid by messenger per year :
100k = 1 naira
10k = (100/10) = 0.1 naira
Hence 0.1 naira is paid as tax on every naira earned
Total amount paid on 2640 Naira :
Amount paid per naira * total amount earned
(0.1 * 2640) = 264 naira
Jake spent a three-day weekend on the lake. On Saturday, he rented a pontoon boat for three hours and paid $435. On Sunday, he rented the same boat for five hours and it cost him $190 more than it di the day before. If he rented the same boat on Monday for just two hours, find the total cost to rent the boat for three days.
Answers
Answer:
1400
Step-by-step explanation:
There is a flat fee involved, which is the y-intercept of the line.
The line eats the points:
(3, 435)
and
(5, 625)
the slope is 190/2 = 95
B = y - mx = 435 - (95)(3)
= 435 - 285
= 150
The linear function is:
y = 95x + 150
So for x=2, it will cost
95(2) + 150 = 190 + 150 = 340
435 + 625 + 340 = 1400
The total cost to rent the boat for three days is $1400.
Given that, on Saturday, he rented a pontoon boat for three hours and paid $435.
What is slope of a line?The slope of the line is the ratio of the rise to the run, or rise divided by the run. It describes the steepness of line in the coordinate plane.
The cost for the rented a pontoon boat for five hours is 435+190 = 625
The coordinate points are (3, 435) and(5, 625)
The slope is m = (625-435)/(5-3)
= 190/2 = 95
Now, b = y - mx = 435 - (95)(3)
= 435 - 285 = 150
So, the linear function is y = 95x + 150
So for x=2, it will cost
95(2) + 150 = 190 + 150 = 340
Total cost = 435 + 625 + 340 = 1400
Therefore, the total cost to rent the boat for three days is $1400.
To learn more about the slope of a line visit:
https://brainly.com/question/14511992.
#SPJ2
which data set is more centered around a high peak??
a. may
b. july
c. neither
d. both
Answers
The correct option a. may.The data shown in the may histogram is more centered around a high peak.
Explain about the histograms:A graph called a histogram is used to show the frequency distribution of a small number of data points for a single variable.
Histograms frequently divide data into different "bins" or "range groups" and count however many points are in each bin.The histogram illustration below shows test results for students. The scores of the student are divided into various ranges. Each bar's height indicates the number of students who received a score within that range.For the given two histograms,
May has the peak value for the frequency of day at 14.
July has the peak value for the frequency of day at 10.
Thus, The data shown in the may histogram is more centered around a high peak.
Know more about the histograms:
https://brainly.com/question/28164315
#SPJ1
Complete question-
which data set is more centered around a high peak??
a. may
b. july
c. neither
d. both
The diagram for the question is shown.

sample size and the confidence level width have a (n) __________ relationship.
Answers
Sample size and the confidence level width have an inverse relationship. As the sample size increases, the confidence level width decreases.
When determining a confidence interval for a population parameter, such as the mean or proportion, a larger sample size provides more information about the population. This increased information leads to a narrower confidence interval.
The confidence level width is influenced by two factors: the sample standard deviation (or the variability of the data) and the critical value associated with the desired confidence level. As the sample size increases, the sample standard deviation becomes a more accurate estimate of the population standard deviation. This reduces the variability and leads to a narrower confidence interval.
A larger sample size leads to a decrease in the confidence level width, providing a more precise estimate of the population parameter with a higher level of confidence.
Learn more about ”confidence interval” here:
brainly.com/question/32546207
#SPJ11
what is 32+(-12 7/8) equal to
Answers
Answer:
153/8
Step-by-step explanation:
Question 1) Find the inverse transform of the function \( F(z)=\frac{z^{3}+2 z+1}{(z-0.1)\left(z^{2}+z+0.5\right)} \) using the partial fractions expansion method.
Answers
The inverse transform of the given function \(F(z)\) is found using the partial fractions expansion method.
To find the inverse transform of \(F(z)\), we first factorize the denominator into its irreducible quadratic factors. In this case, the denominator is \((z-0.1)(z^2+z+0.5)\).
Next, we perform partial fractions expansion by expressing \(F(z)\) as the sum of simpler fractions with denominators corresponding to the irreducible factors. We assume the form of the partial fractions to be \(F(z) = \frac{A}{z-0.1} + \frac{Bz+C}{z^2+z+0.5}\).
By equating the numerator of the original function to the sum of the numerators of the partial fractions, we can solve for the unknown constants A, B, and C.
Once the constants are determined, the inverse transform of each partial fraction can be found using table lookups or the inverse transform formulas.
Finally, the inverse transform of \(F(z)\) is the sum of the inverse transforms of the partial fractions, resulting in the expression in the time domain.
It's important to note that this summary provides a general overview of the partial fractions expansion method for finding inverse transforms. In practice, the calculations may involve more complex algebraic manipulations to determine the constants and find the inverse transforms.
Learn more about inverse transforms: brainly.com/question/27753787
#SPJ11
Find the solution of the following initial value problem.g'(x)= 3x(x^2 -1/3) ; g(1) = 2
Answers
According to the question we have the solution of the given differential equation initial value problem is: g(x) = (3/4)x^4 - x + 9/4 .
To solve the given initial value problem, we need to integrate both sides of the differential equation. We have:
g'(x) = 3x(x^2 - 1/3)
Integrating both sides with respect to x, we get:
g(x) = ∫[3x(x^2 - 1/3)] dx
g(x) = ∫[3x^3 - 1] dx
g(x) = (3/4)x^4 - x + C
where C is the constant of integration.
To find the value of C, we use the initial condition g(1) = 2. Substituting x = 1 and g(x) = 2 in the above equation, we get:
2 = (3/4)1^4 - 1 + C
2 = 3/4 - 1 + C
C = 9/4
Therefore, the solution of the given initial value problem is:
g(x) = (3/4)x^4 - x + 9/4
In more than 100 words, we can say that the given initial value problem is a first-order differential equation, which can be solved by integrating both sides of the equation. The resulting function is a family of solutions that contain a constant of integration. To find the specific solution that satisfies the initial condition, we use the given value of g(1) = 2 to determine the constant of integration. The resulting solution is unique and satisfies the given differential equation as well as the initial condition.
To know more about differential visit :
https://brainly.com/question/31383100
#SPJ11
Find the value of k if the line y = kx +4 goes through the point (5, -9).
Plz help
Answers
Answer:
k=-13/5
Step-by-step explanation:
y=kx+4
-9=k(5)+4
-9=5k+4
-9-4=5k
5k=-13
k=-13/5
On putting the values of the point in the equation of line, the value of \(k\) is \(-\frac{13}{5}\).
When a line passes through a point, the point satisfies the equation of the line.
The line \(y = kx +4\) goes through the point \((5, -9)\).
So, \((5,-9)\) must satisfy the equation of the line.
Put \(x=5\) and \(y=-9\) in the equation \(y = kx +4\).
\(-9=k(5)+4\)
\(-9=5k+4\)
\(-9-4=5k\)
\(-13=5k\)
\(-\frac{13}{5}=k\)
So, the value of \(k\) is \(-\frac{13}{5}\).
Learn more here:
https://brainly.com/question/14566987?referrer=searchResults

How to do ascending order with the symbols
Best answer will be marked the brainliest
Answers
Answer:
Less than symbol (<)
Step-by-step explanation:
For example:
A set of numbers that are in ascending order
1<2<3<4<5<6<7<8<9<10
The less than symbol is used to denote the increasing order.
Hope this helps
How many solutions does the equation 2(3x + 4) = 6x + 8 have?
Answers
Answer:
Infinitely many solutions
Step-by-step explanation:
2(3x+4)=6x+8
6x+8=6x+8
Therefore, there are infinitely many solutions because both sides will always be equal to each other since they have the same slope and y-intercept.
Branliest For Correct answer
Please I need help
Factor Completely
a^2 - a - 20
Answers
Answer:
\(\left(a+4\right)\left(a-5\right)\)
Step-by-step explanation:
Break the expression into groups.
=(a^2+4a)+(−5a−20)
Factor out a from a2+4a: a(a+4)
Factor out −5 from −5a−20: −5(a+4)
=a(a+4)−5(a+4)
Which graph shows a system of equations with exactly one solution?\
Answers
Answer:
The graph of such system of equations should show two lines with different slopes, and therefore intersecting in one unique point.
Step-by-step explanation:
In order to have a system of linear equations in two variables give as answer only one solution (that is a unique point on the plane), the graph of such equations should be two lines with different slopes, and therefore intersecting in one unique point.
Graphs with parallel lines will not be correct since there is no intersection, and therefore no answer to such systems.
Graphs that show lines that overlap are not an answer either, since in such case there are infinite number of solutions (all the points on each line)
Answer:D
Step-by-step explanation: