Angle 1 and 2 are vertical angles. If angle one
equals 55 degrees. What does the other angie
equal?
Answers
Related Questions
Eva sees a dolphin 3.23.23, point, 2 meters below sea level and a bird \dfrac{47}{10} 10 47 start fraction, 47, divided by, 10, end fraction meters above sea level. Which of the expressions represents the vertical distance between the dolphin and the bird?
Answers
Answer:
47/10 - 3.2
Step-by-step explanation:
Given
Dolphin = 3.2
Bird = 47/10
Required
What is the vertical distance between both
Using a vertical scale;
Represent the bird "above sea level" position with positive and dolphin at "below sea level" position with negative.
The vertical distance between them is as follows;
Distance = +[Above The Sea] - [Below The Sea]
Distance = +47/10 - 3.2
Distance = 47/10 - 3.2
Hence, the vertical distance between both is 47/10 - 3.2
A polygon has 15 sides.
(b) If the sum of seven of the exterior angles is 200°, find the sum of the
eight interior angles not adjacent to these exterior angles.

Answers
(a) correct
(b) The exterior angles of a polygon add to 360°, so the other 8 interior angles add to 160°. Since an exterior angle and its corresponding interior angle add to 180°, the 8 exterior-interior angle pairs we must consider add to 1440°. Thus, the answer is 1280°.
Evaluate. [2−∣∣−23−2(−15)∣∣]÷(−13) what is the value of the expression? enter your answer as a simplified fraction in the box.
Answers
To evaluate the expression [2−||−23−2(−15)||]÷(−13), we need to follow the order of operations, which is also known as PEMDAS (Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction).
First, let's simplify the absolute value:
||−23−2(−15)|| = ||−23+30|| = ||7|| = 7
Next, let's substitute this simplified value back into the original expression:
[2−7]÷(−13)
Now, we can simplify the expression further:
2−7 = −5
Finally, divide −5 by (−13):
−5÷(−13) = 5/13
Therefore, the value of the expression is 5/13.
The value of the expression:
[2−||−23−2(−15)||]÷(−13) is 5/13.
To evaluate the given expression [2−||−23−2(−15)||]÷(−13), we start by simplifying the absolute value within the expression. We substitute the expression inside the absolute value with its simplified form: −23+30 = 7. The absolute value of 7 is 7. Now, we substitute this value back into the original expression: [2−7]÷(−13). Simplifying further, we have 2−7 = −5. Finally, we divide −5 by (−13) to get 5/13. In conclusion, the value of the given expression is 5/13.
The value of the expression [2−||−23−2(−15)||]÷(−13) is 5/13.
To learn more about simplified form visit:
brainly.com/question/28401329
#SPJ11
Solve for s.
S-1
2
+3
S
Answers
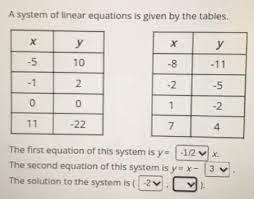
Select the correct answer from each drop-down menu. A system of linear equations is given by the tables. x y -5 10 -1 2 0 0 11 -22 x y -8 -11 -2 -5 1 -2 7 4 The first equation of this system is y = x. The second equation of this system is y = x − . The solution to the system is ( , ).
Answers
For the linear equations provided by the coordinates in the table;
The first equation of this system is y = -2x.
The second equation of this system is y = x - 3.
The solution to the system is (1, -2).
How do we solve for the system of linear equation?We have four points (-5,10), (-1,2), (0,0), and (11,-22) for first equation, and four points (-8,-11), (-2,-5), (1,-2), and (7,4) the second equation.
The slope (m) is given by the formula (y2 - y1) / (x2 - x1).
For the first line, we can use the points (-5,10) and (-1,2)
m1 = (2 - 10) / (-1 - (-5)) = -8/4 = -2.
the first equation is y = -2x
the second line, we can use the points (-8,-11) and (-2,-5)
m2 = (-5 - -11) / (-2 - -8) = 6/6 = 1.
the second line has a slope of 1,
the equation should have the form y = x + c.
To find c, we can use one of the points, for instance (-2,-5):
-5 = -2 + c => c = -5 + 2 = -3.
So, the second equation is y = x - 3.
the solution to the system, we need to find where the two lines intersect.
y = -2x
y = x - 3
Setting both equation equally
-2x = x - 3
=> 3x = 3
=> x = 1.
Substituting x = 1 into the first equation
y = -2(1) = -2.
the solution to the system of linear equation would be (1, -2).
Find more exercises on linear equation;
https://brainly.com/question/29739212
#SPJ1
A number divided by eight answers 27 remainders four whats the number
Answers
As per the query, we have to find a number which is divided by 8 that answers 27, i.e., quotient is 27, and remainder is 4. The number is 220.
In this case, we used it to find the number that was divided by 8 and gave a quotient of 27 and a remainder of 4. As we know the rule:
Dividend = Divisor × Quotient + Remainder
x = 8 × 27 + 4 x = 216 + 4 x = 220.
Hence, the number is 220.
The formula I used is called the division algorithm. It’s a way to divide two numbers and get a quotient and remainder. We can use this formula to solve other division problems with remainders as well.
To know more about division algorithm, refer:
https://brainly.com/question/27893941
#SPJ4
what is the probability that a randomly selected vehicle's speed exceeds the speed limit of 70 m/h? (round your answer to four decimal places.)
Answers
The probability of a magnitude 7.0-7.9 earthquake in the Los Angeles area in the next 30 years is approximately 0.252.
If the recurrence interval of a magnitude 7.0-7.9 earthquake in the Los Angeles area is 95 years, then the probability of such an earthquake occurring in any given year is:
P = 1/95
The probability of at least one such earthquake occurring in the next 30 years can be found using the complementary probability:
P(complement) = 1 - P(event)
where P(event) is the probability of the event occurring.
So, the probability of at least one magnitude 7.0-7.9 earthquake occurring in the Los Angeles area in the next 30 years is:
P(complement) = 1 - (1/95)³⁰
P(complement) ≈ 0.252
To know more about probability here
https://brainly.com/question/14210034
#SPJ4
The sum of two consecutive numbers is 25. What is the largest of the consecutive numbers? Type a numerical answer in the space provided.
Answers
In a case whereby the sum of two consecutive numbers is 25 the largest of the consecutive numbers is 13.
How can the the largest of the consecutive numbers be calculated?Given that sum of two consecutive numbers is 25 , ans we were required to locatye the largest of the consecutive numbers. The we can represent the consecutive numbers as x and x+1. According to the problem, the sum of these two consecutive numbers is 25:
x + (x+1) = 25
Simplifying the left side of the equation:
2x + 1 = 25
2x = 24
Dividing both sides by 2:
x = 12
So the first consecutive number is 12. The second consecutive number is 12 + 1 = 13. Therefore, the largest of the consecutive numbers is 13.
Learn more about consecutive numbers at:
https://brainly.com/question/26352026
#SPJ1
(6)/(a^(2))+(5a^(-2))/(3^(-3))
Answers
Answer:
\(\frac{141}{a^{2} }\)
Step-by-step explanation:
\(\frac{6}{a^{2} } + \frac{5a^{-2} }{3^{-3} }\)
\(\frac{141}{a^{2} }\)
Find the vertex of f(x)= x^2+ 6x + 36
Pls help soon
Answers
Answer:
vertex(-3,27)
Step-by-step explanation:
f(x)= x^2+ 6x + 36 ( a=1,b=6,c=36)
V(h,k)
h=-b/2a=-6/2=-3
k=f(-3)=3²+6(-3)+36
f(-3)=9-18+36=27
vertex(-3,27)
For her final project, stacy plans on surveying a random sample of students on whether they plan to go to florida for spring break. From past years, she guesses that about % of the class goes. Is it reasonable for her to use a normal model for the sampling distribution of the sample proportion? why or why not?.
Answers
Less than 10 attempts were successful in this situation. due to the fact that 5 is less than 10. The data does not satisfy the requirement as a result.
Because the data don't fit the success or failure criteria, it is not appropriate to adopt a normal model for the sampling distribution of the sample.
50 students make up the sample. The likelihood that she assumes 10% of the class will attend is 10%. It will be demonstrated by:
1 - p = 1 - 10%
⇒ 1 - 0.10 = 0.90
np = 50 × 0.1
np = 5
This suggests the number of victories.
In this case, fewer than 10 efforts have been successful. Since 5 is less than 10, this is the situation. The data does not meet the criteria as a result.
To know more about Sampling, refer to this link:
https://brainly.com/question/24466382
#SPJ4
You are on a fishing trip with your friends. The diagram shows the location of the river, fishing hole, campsite, and bait store. The campsite is located 200 feet from the fishing hole. The bait store is located 110 feet from the fishing hole. How wide is the river?.
Answers
the width of the river is approximately 64.03 feet.
To determine the width of the river, we can use the concept of triangle similarity.
Let's assume that the river width is represented by the variable "x".
From the information given, we have a right triangle formed by the river, the fishing hole, and the campsite. The campsite is located 200 feet from the fishing hole, and the river width is the unknown side.
Using the Pythagorean theorem, we can set up the equation:
x^2 + 200^2 = (200 + 110)^2
Simplifying the equation:
x^2 + 40000 = 44100
x^2 = 44100 - 40000
x^2 = 4100
Taking the square root of both sides:
x = sqrt(4100)
x ≈ 64.03 feet
Therefore, the width of the river is approximately 64.03 feet.
to know more about equation visit:
brainly.com/question/649785
#SPJ11
Which is the first step in solving
X-2 = 2?
Answers
Answer:
The first step is to find a number that when subtracted from 2 gives you 2.
Step-by-step explanation:
The algebraic part of this problem would be to add the -2 (adding 2 to both sides) to both sides, so
first x-2=2, then x-2(+2)=2(+2) which would give us,
x=4
*note: the parenthesis are just to show that we are adding the 2, to make it more understandable.
Find the ODE that determines the family of all circles passing through the points \( (1,0) \) and \( (-1,0) . S \)
Answers
To find the ODE that determines the family of all circles passing through the points (1,0) and (-1,0), we must first find the general equation for a circle. The equation of a circle with center (h,k) and radius r is given by:
\((x - h)^2 + (y - k)^2\)
\(= r^2\)
If a circle passes through the points (1,0) and (-1,0), then its center lies on the perpendicular bisector of the segment joining these two points.
The perpendicular bisector is the line x = 0.
Hence, the center of the circle lies on the line x = 0.
The distance between the center of the circle and the point (1,0) is equal to the distance between the center and the point (-1,0). This is because both of these points lie on the circle.
Hence, the center of the circle lies on the line x = 0 and has the form (0,y).
Let the radius of the circle be r. Then, we have:
\((1 - 0)^2 + (0 - y)^2 \\= r^2 and (-1 - 0)^2 + (0 - y)^2 \\= r^2\)
Simplifying these equations, we get:
\(y^2 + 1 = r^2 ... (1)y^2 + 1 = r^2 ...\)
(2)Equating the right-hand sides of equations (1) and (2), we get:
\(r^2 = y^2 + 1\)
The general equation for a circle passing through \((1,0) and (-1,0)\).
To know more about circles passing through the points visit:
https://brainly.com/question/23948918
#SPJ11
HELP please this is due soon

Answers
Answer:
Step-by-step explanation:
Side Opposite to ∠x is called YZ
The side Opposite to ∠y is called XZ (that's the hypotenuse of the triangle)
Side Opposite to ∠Z is XY
Answer:
Side apposite to angle X is YZ
Side apposite to angle Y is XZ
Side apposite to angle Z is XY
Hope this helps you
have a great day
replace ??null hypothesis value?? with the mean value of the relative skill under the null hypothesis.
Answers
It is not generally recommended to replace the null hypothesis value with the mean value of the relative skill under the null hypothesis.
The null hypothesis value represents a specific hypothesis or claim that is being tested, and it is usually set based on prior knowledge or assumptions about the population being studied.
Replacing the null hypothesis value with the mean value of the relative skill under the null hypothesis may lead to biased or inaccurate results, as it may not accurately represent the true hypothesis or claim being tested. It is important to carefully consider the null hypothesis value and set it appropriately based on prior knowledge or assumptions about the population being studied.
To learn more about null hypothesis please click on below link.
https://brainly.com/question/30351745
#SPJ4
Replace null hypothesis value with the mean value of the relative skill under the null hypothesis?
What is -15+6z=-8z+13???
Answers
Answer:
z=2
Step-by-step explanation:
add 15 to both sides.
6z=-8z+28
add 8z to both sides.
14z=28
divide by 14 on both sides.
z=2
Answer:
z=2
Step-by-step explanation:
-15+6z=-8z+13
6z=-8z+28
14z=28
z=2
A _______ random variable has infinitely many values associated with measurements.
Answers
Answer:
Continuous
A continuous random variable has infinitely many values, and those values can be associated with measurements on a continuous scale in such a way that there are no gaps or interruptions.
How many Real solutions

Answers
Answer:
A. 2 real roots: (2, 7) and (1, 4).
Step-by-step explanation:
y = x^2 + 3
y = 3x + 1
So equating the right sides:
x^2 + 3 = 3x + 1
x^2 - 3x + 2 = 0
(x - 2)(x - 1) = 0
So there are 2 roots.
They are x = 2 , y = 3(2) + 1 = 7 and
x = 1, y = 3(1) +1 = 4.
PLZZZZZZ HELP! Find the area.

Answers
Answer:
14.88 km
Step-by-step explanation:
add both base 1 and base 2 together divide them by 2 then multiply by the height.
Can some one help mẹ pls....

Answers
Answer:
h(2) or h(g(4)) = -28
Step-by-step explanation:
g(t) = t - 2,
g(4) = 4 - 2,
g(4) = 2
h(t) = -3t³ - 2t,
h(2) = -3(2)³ - 2(2),
h(2) = -24 - 4,
h(2) or h(g(4)) = -28
If Profit Tk.100000 from reduced tk. 190000. What will be the profit reduce rate
Answers
Answer:
the profit reduced rate is -0.4737
Step-by-step explanation:
The computation of the profit reduced rate is shown below:
= (100,000 - 190,000)÷ (190,000)
= -90,000 ÷ 190,000
= -0.4737
hence, the profit reduced rate is -0.4737
We simply takes the difference and then divided it by 190,000
x less than or equal to negative 7

Answers
Answer:
-11
Step-by-step explanation:
if a is a stochastic matrix, then its 1-eigenspace must be a line.true/false
Answers
Answer: True.
By definition, a stochastic matrix is a square matrix where each entry is a non-negative real number and the sum of each row is 1.
If A is a stochastic matrix and v is a vector in its 1-eigenspace, then we have:
Av = λv
where λ = 1 is the corresponding eigenvalue.
Multiplying both sides by 1/λ = 1, we get:
v = A v
This means that the vector v is also in the range of A, which is a subspace of the vector space R^n.
Since A is a stochastic matrix, the rows of A sum to 1, and therefore the columns of A also sum to 1. This implies that the vector of all 1's, which we denote by u, is also in the range of A.
Since v is a nonzero vector in the 1-eigenspace and u is a nonzero vector in the range of A, the span of v and u is a two-dimensional subspace of R^n.
Moreover, since A is a stochastic matrix, we have:
Au = u
This means that the vector u is also in the 1-eigenspace.
Therefore, the 1-eigenspace of A is a line spanned by the vector u, which is a nonzero vector in the range of A.
if a is a stochastic matrix, then its 1-eigenspace must be a line: True.
A stochastic matrix is a square matrix with non-negative entries where each row sums to one. The 1-eigenspace of a matrix is the set of all eigenvectors with eigenvalue 1.
Let v be an eigenvector of a stochastic matrix A with eigenvalue 1. Then we have Av = 1v.
Multiplying both sides by the transpose of v, we get v^T Av = v^T v.
Since A is a stochastic matrix, its columns sum to 1 and therefore, its transpose has rows that sum to 1. Thus, v^T Av = 1 and v^T v = 1.
This implies that v^T (A-I) = 0, where I is the identity matrix. Since A is stochastic, I is also stochastic and has a unique 1-eigenspace, which is a line spanned by the vector (1,1,....1)^T.
Therefore, v must be a scalar multiple of (1,1,....1)^T, which implies that the 1-eigenspace of A is a line.
Therefore, the statement "if a is a stochastic matrix, then its 1-eigenspace must be a line" is true.
To know more about eigenvectors, visit:
https://brainly.com/question/31013028
#SPJ11
Find the exact values of the six trigonometric ratios of the angle θ in the triangle. sin(θ)=□ cos(θ)=□ tan(θ)= csc(θ)=□ sec(θ)=□ cot(θ)=
Answers
sin(θ) = □
cos(θ) = □
tan(θ) = □
csc(θ) = □
sec(θ) = □
cot(θ) = □
To find the exact values of the trigonometric ratios of angle θ, we need more information about the triangle. Trigonometric ratios are defined based on the ratios of the sides of a right triangle. In order to calculate these ratios, we need to know the lengths of the sides of the triangle or have additional information about the angle.
Without specific values or additional information about the triangle, we cannot determine the exact values of the trigonometric ratios. Each trigonometric ratio (sine, cosine, tangent, cosecant, secant, and cotangent) requires different side lengths of the triangle to be calculated accurately.
Trigonometry and how trigonometric ratios are defined based on the relationships between the sides of a right triangle. Trigonometry is a branch of mathematics that deals with the properties and relationships of angles and triangles. By studying trigonometry, you can gain a deeper understanding of how angles and sides are connected and how they can be used to solve various mathematical and real-world problems.
Learn more about trigonometric
brainly.com/question/29156330
#SPJ11
Brainliest + 50 points for answer

Answers
Multiply first cause it’s in the parentheses. To multiply fractions you go straight across
1/2 x 3/8
1 x 3 = 3
2 x 8 = 16
So you get
3/16
When dividing fractions you have to flip the second fraction and multiply the same.
So 3/4 divided by 3/16
Flip 3/16 to 16/3
So now
3/4 x 16/3
16 x 3 = 48
4 x 3 = 12
48/12
Simplified is 4
Answer:
A) 4
Multiply first cause it’s in the parentheses. To multiply fractions you go straight across
1/2 x 3/8
1 x 3 = 3
2 x 8 = 16
So you get
3/16
When dividing fractions you have to flip the second fraction and multiply the same.
So 3/4 divided by 3/16
Flip 3/16 to 16/3
So now
3/4 x 16/3
16 x 3 = 48
4 x 3 = 12
48/12
Simplified is 4
Step-by-step explanation:
4−(−8)= please help i need it now
Answers
Answer:
Step-by-step explanation:
Use the graph to complete the statement.
The triangle at the top of the graph is a reflection of the
triangle at the bottom.
Over what line is the triangle reflected?
The triangle is reflected over line _________

Answers
Answer:
C
Step-by-step explanation:
I know my reflections =D
Mark as brainliest ;D
Answer:
c
Step-by-step explanation:
Is the following model linear? (talking about linear regression model)
y^2 = ax_1 + bx_2 + u.
I understand that the point is that independent variables x are linear in parameters (and in this case they are), but what about y, are there any restrictions? (we can use log(y), what about quadratic/cubic y?)
Answers
In a linear regression model, the linearity assumption refers to the relationship between the independent variables and the dependent variable.
It assumes that the dependent variable is a linear combination of the independent variables, with the coefficients representing the effect of each independent variable on the dependent variable.
In the given model, y^2 = ax_1 + bx_2 + u, the dependent variable y is squared, which introduces a non-linearity to the model. The presence of y^2 in the equation makes the model non-linear, as it cannot be expressed as a linear combination of the independent variables.
If you want to include quadratic or cubic terms for the dependent variable y, you would need to transform the model accordingly. For example, you could use a quadratic or cubic transformation of y, such as y^2, y^3, or even log(y), and include those transformed variables in the linear regression model along with the independent variables. This would allow you to capture non-linear relationships between the dependent variable and the independent variables in the model.
Learn more about linearity here
https://brainly.com/question/2030026
#SPJ11
Which of the following statements must be true based on the diagram below?

Answers
Answer: CG is a segment bisector.
Step-by-step explanation:
A segment bisector splits a segment into two equal parts. Notice the marks on FG and GE. The marks are showing that FG and GE are of equal length, therefore CG is bisecting segment FE into two equal segments.