Analysis of variance is the most common inferential statistical procedure used to analyze experiments because O there are several different versions of it, and so it can be used to compare the effect of many different groups and variables there is one version of it and it is better for comparing two group more accurately than the two-sample tests. O it is the only statistical procedure that can test either between-subjects factors or within- subjects factors. O most researchers are more interested in differences between the population and one sample
Answers
Option-A is It comes in a variety of forms, making it possible to compare the effects of numerous groups and variables satisfy the statement.
Given that,
The most typical inferential statistical method used to evaluate trials is analysis of variance because
We have to find which of the options are suitable for the given statements.
Option-A is It comes in a variety of forms, making it possible to compare the effects of numerous groups and variables satisfy the statement.
Option-B is It comes in one form, and compared to two-sample tests, it is more accurate for comparing two groups does not satisfy the statement.
Option-C is It is the only statistical method that can test both within- and between-subjects factors does not satisfy the statement.
Option-D is The majority of academics are more focused on differences between one sample and the population as a whole does not satisfy the statement.
To learn more about variables visit: https://brainly.com/question/29209545
#SPJ4
Related Questions
Find the product. 5.2 × 10.38
Answers
Answer:
The answer would be approximately 53.976
Step-by-step explanation:
Answer:
53.976
Step-by-step explanation:
5.2 × 10.38 = 53.976I hope this helps!
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
Find the surface area of a cylinder with a height of 9 ft and diameter of 4

Answers
Answer:50.2654812288
Step-by-step explanation:
The two circles :
Sa = πr²
= π x 2²
= 12.5663706144
= 12.5663706144 x 2
= 25.1327412288
The rectangle :
C x h = 2πr
= 25.13274
= 25.13274 + 25.1327412288
= 50.2654812288
Step-by-step explanation:
50.2654858683848
because it is equivalent to this. Also I can tutor you
real-estate agent conducted an experiment to test the effect of selling a staged home vs. selling an empty home. To do so, the agent obtained a list of 10 comparable homes just listed for sale that were currently empty. He randomly assigned 5 of the homes to be "staged," meaning filled with nice furniture and decorated. The owners of the 5 homes all agreed to have their homes staged by professional decorators. The other 5 homes remained empty. The hypothesis is that empty homes are not as appealing to buyers as staged homes and, therefore, sell for lower prices than staged homes. The mean selling price of the 5 empty homes was $150,000 with a standard deviation of $22,000. The mean selling price of the 5 staged homes was $175,000 with a standard deviation of 35,000. A dotplot of each sample shows no strong skewness and no outliers.
Answers
Real-estate agent tested the effect of staging on home sale prices. Out of 10 comparable homes, 5 were staged. Staged homes sold for $15k more on average, with no skewness or outliers.
Based on the information given, the real-estate agent conducted an experiment to test the effect of selling a staged home vs. selling an empty home.
The hypothesis is that empty homes sell for lower prices than staged homes. The agent randomly assigned 5 empty homes to be staged and obtained a list of 10 comparable homes.
The mean selling price of the 5 empty homes was $150,000 with a standard deviation of $22,000. The mean selling price of the 5 staged homes was $175,000 with a standard deviation of 35,000. There was no strong skewness or outliers in the dot plots of the two samples.
To know more about standard deviation:
https://brainly.com/question/23907081
#SPJ1
(x+3)=8y-84
Solve for x
help asap
Answers
Answer:
\(\boxed{\bf\purple{x=8y−87}}\)
Step-by-step explanation:
Let's solve for x.
x+3=8y−84
Step 1: Add -3 to both sides.
x+3+−3=8y−84+−3
x=8y−87
Therefore,Answer is :
\(\boxed{x=8y−87}\)
Answer:
\( \longmapsto \sf(x + 3) = 8y - 84\)
\(\longmapsto \sf \: x + 3 = 8y - 84\)
\(\longmapsto \sf \: x = 8y - 84 - 3\)
\(\longmapsto \sf \: x = 8y -87 \)
Thus,the value of x is 8y-87.each function
f(x)=-4x-5;
ion for
Find ƒ(1)
for the given
Answers
When x is equal to 1, the Function f(x) = -4x - 5 yields a value of -9.
The find ƒ(1) for the function f(x) = -4x - 5, we need to substitute x = 1 into the function and evaluate the expression.
Replacing x with 1, we have:
ƒ(1) = -4(1) - 5
Simplifying further:
ƒ(1) = -4 - 5
ƒ(1) = -9
Therefore, when x is equal to 1, the value of the function f(x) = -4x - 5 is ƒ(1) = -9.
Let's break down the steps taken to arrive at the solution:
1. Start with the function f(x) = -4x - 5.
2. Replace x with 1 in the function.
3. Evaluate the expression by performing the necessary operations.
4. Simplify the expression to obtain the final result.
In this case, substituting x = 1 into the function f(x) = -4x - 5 gives us ƒ(1) = -9 as the output.
It is essential to note that the notation ƒ(1) represents the value of the function ƒ(x) when x is equal to 1. It signifies evaluating the function at a specific input value, which, in this case, is 1.
Thus, when x is equal to 1, the function f(x) = -4x - 5 yields a value of -9.
For more questions on Function .
https://brainly.com/question/11624077
#SPJ8
Matthew invested $8,000 in an account paying an interest rate of 3 1/8% compounded
continuously. Parker invested $8,000 in an account paying an interest rate of 2 3/4%
compounded annually. To the nearest dollar, how much money would Parker have in
his account when Matthew's money has tripled in value?
Answers
Parker would have approximately $13,774 in his account when Matthew's money has tripled in value.
We have,
For Matthew's investment, the continuous compounding formula can be used:
\(A = P \times e^{rt}\)
Where:
A = Final amount
P = Principal amount (initial investment)
e = Euler's number (approximately 2.71828)
r = Annual interest rate (in decimal form)
t = Time (in years)
In this case,
Matthew's money has tripled,
So A = 3P.
For Parker's investment, the formula for compound interest compounded annually is used:
\(A = P \times (1 + r)^t\)
Where:
A = Final amount
P = Principal amount (initial investment)
r = Annual interest rate (in decimal form)
t = Time (in years)
We need to find t when Matthew's money has tripled in value.
Let's set up the equation:
\(3P = P \times e^{rt}\)
Dividing both sides by P, we get:
\(3 = e^{rt}\)
Taking the natural logarithm of both sides:
ln(3) = rt
Now we can solve for t
t = ln(3) / r
For Matthew's investment,
r = 3 1/8% = 3.125% = 0.03125 (as a decimal).
For Parker's investment,
r = 2 3/4% = 2.75% = 0.0275 (as a decimal).
Now we can calculate t for Matthew's investment:
t = ln(3) / 0.03125
Using a calculator, we find t ≈ 22.313 years.
Now, we can calculate how much money Parker would have in his account at that time:
\(A = P \times (1 + r)^t\)
\(A = $8,000 \times (1 + 0.0275)^{22.313}\)
Using a calculator, we find A ≈ $13,774.
Therefore,
Parker would have approximately $13,774 in his account when Matthew's money has tripled in value.
Learn more about compound interest here:
https://brainly.com/question/13155407
#SPJ1
Answer:
20,763
Step-by-step explanation:
I saw the answer after I got it wrong
it takes 3/5 of a gallon of paint to cover 2/3 of a wall. how many gallons is this per wall
Answers
Answer:
9/10
Step-by-step explanation:
3/5 gallon paint = 2/3 of wall
if you divide 3/2 each side then...
9/10 gallon of paint = 1 wall
Answer:
1/5 of a wall
Step-by-step explanation:
if you take 3/5 and divide it by 2/3 then you get 1/5
Use the graph to write a formula for the polynomial function of the least degree

Answers
Answer:
0.5 degrees is the answer you divided the quotion by 5 then get your answer (this isnt actually the answer lol)
Step-by-step explanation:
a rectangle with a width of 30 centimeters has a perimiter of 100 centimeters to 160 centimeters graph a compound inequality
Answers
Answer:
5 ≤ L ≤ 35
Step-by-step explanation:
Let w represent the width of the rectangle.
The perimeter (P) of the rectangle is given by:
P = 2w + 2L
Where L is the length of the rectangle.
We know that w = 30 cm and that the perimeter is between 100 and 160 cm. We can now set up our compound inequality:
100 ≤ 2(30) + 2L ≤ 160
100 ≤ 90 + 2L ≤ 160
10 ≤ 2L ≤ 70
We can now divide both sides by 2 to solve for L:
5 ≤ L ≤ 35
Therefore, the compound inequality that represents the graph of a rectangle with a width of 30 centimeters and a perimeter of 100 centimeters to 160 centimeters is: 5 ≤ L ≤ 35
Kevin has $97,800 in a savings account that earns 2% interest per year. The interest is not
compounded. How much will he have in total in 4 months?
Answers
HELP ME PLEASE!!!!!!!!!!!!

Answers
1) The three main trigonometric ratios of the given triangle are:
sin B = 5/9.43
cos B = 8/9.43
tan B = 5/8
2) The measure of angle A is: ∠A = 39.6°
3) The length of side x is: x = 39.5 mm
How to find the trigonometric ratios?The six trigonometric ratios of a right angle triangle are:
sin x = opposite/hypotenuse
cos x = adjacent/hypotenuse
tan x = opposite/adjacent
cot x = 1/tan x
sec x = 1/cos x
cosec x = 1/sin x
1) The three main trigonometric ratios of the given triangle are:
sin B = 5/9.43
cos B = 8/9.43
tan B = 5/8
2) The measure of angle A is gotten from:
∠A = cos⁻¹ (47/61)
∠A = 39.6°
3) The length of side x using trigonometric ratios is:
21/x = tan 28
x = 21/tan 28
x = 39.5 mm
Read more about Trigonometric ratios at: https://brainly.com/question/13276558
#SPJ1
Assignment: Find the Volume

Answers
Key:
Volume formulas:
• length × width × height
• a³
Step-by-step explanation:
1. \(5 * 2 * 7 = 70\)
2. \(10^3 = 1000\)
3. \(7^3 = 343\)
4. \(5 * 1 * 6 = 30\)
5. \(6 * 4 * 2 = 48\)
-----------------------------------------------------------------------------------------------------------
Answer:
1. 70
2. 1000
3. 343
4. 30
5. 48
Henry's garden which is 1/4 of an acre is to be divided into 12 equal size areas what is the size of each area?
Answers
The size of each area is 3x
Word problems in mathematics involve arithmetic operations and algebraic equations employed to solve real-life cases.
From the given parameters.
Henry's garden is said to be 1/4 of an acre.If an acre = xThen, Henry's garden is (1/4)xSo, Henry's garden is said to be divided into 12 equal size areas.
∴
The size of each area is;
\(\mathbf{= \dfrac{\dfrac{1}{4}x}{12}}\)
\(\mathbf{= \dfrac{1}{4}(x) \times \dfrac{12}{1}}\)
= 3x
Learn more about word problems in mathematics here:
https://brainly.com/question/21405634
please help me thank youuu
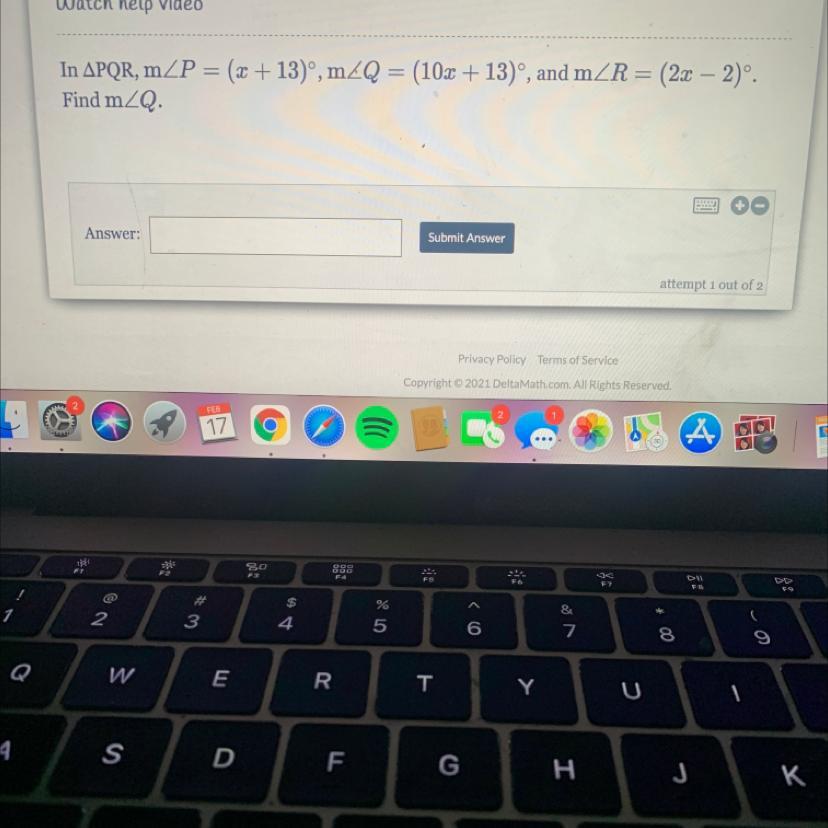
Answers
Answer:
m<Q = 133°
Step-by-step explanation:
From the question given above, the following data were obtained:
m<P = (x + 13)°
m<Q = (10x + 13)°
m<R = (2x – 2)°
m<Q =?
Next, we shall determine the value of x. This can be obtained as follow:
m<P + m<Q + m<R = 180 (sum of angles in a triangle)
(x + 13)° + (10x + 13)° + (2x – 2)° = 180
x + 13 + 10x + 13 + 2x – 2 = 180
x + 10x + 2x + 13 + 13 – 2 = 180
13x + 24 = 180
Collect like terms
13x = 180 – 24
13x = 156
Divide both side by 13
x = 156 / 13
x = 12
Finally, we shall determine m<Q. This can be obtained as follow:
m<Q = (10x + 13)°
x = 12
m<Q = 10(12) + 13
m<Q = 120 + 13
m<Q = 133°
what 2-1+46-2x0
I tried O but it didn't work
Answers
Answer:
answer is 47
Step-by-step explanation:
use the rule, 2x0 = 0 then (2- 1) that's 1 and then (46-0) that's 46 so 1 + 46 is 47
Writing in Math Explain how you could convert a rate of miles
per hour to a rate of miles per second.
Answers
Answer:
divide the speed value by 3600
according to the most used browser by the name of g
Step-by-step explanation:
The graphs below have the same shape. What is the equation of the red
graph?

Answers
Step-by-step explanation:
If they have the same shape, the red graph is a translation of the blue, which is given to be y=x^2.
Since the red graph stays on the y axis at two units above the blue (y=x^2) curve, therefore the red curve is given by y=x^2+2.
The equation of the red graph is f(x) = x² + 2.
Option B is the correct answer.
What is an equation?An equation contains one or more terms with variables connected by an equal sign.
Example:
2x + 4y = 9 is an equation.
2x = 8 is an equation.
We have,
The graphs of f(x) = x² and f(x) = x² + 2 are both quadratic functions, which means they have a parabolic shape.
The graph of f(x) = x^2 is an upward-opening parabola with its vertex at the origin (0,0).
The parabola is symmetric about the y-axis and the x-axis.
The graph of f(x) = x² + 2 is also an upward-opening parabola, but it has been shifted upward by 2 units compared to the graph of f(x) = x².
This means that the vertex of the parabola has been shifted from (0,0) to (0,2).
Thus,
The equation of the red graph is f(x) = x² + 2.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ7
HELP ASAP
sorry for the cracked ipad
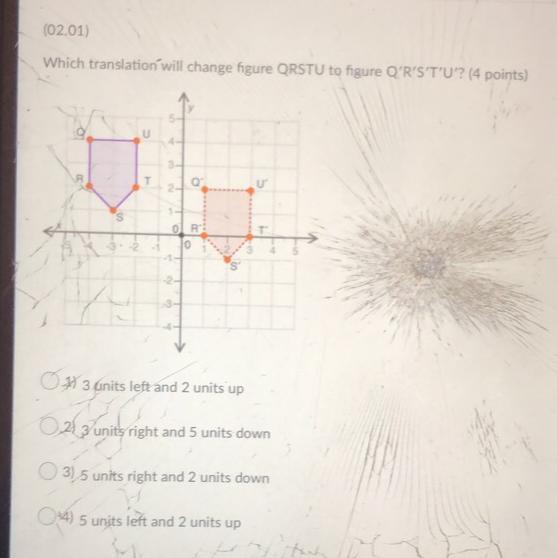
Answers
The answer is 3) 5 units to the right and 2 units down.
How I solved this:
I used the point T and translated it to point T'. I counted 5 units to the right and counted 2 units down. The translation would be T(-2, 5).
Hi , the answer I choose was wrong , what is the correct answer ? Will choose brainlest so be quick

Answers
Answer:
Not congruent
Step-by-step explanation:
Missing angel Q andK
Find the equation of the line in slope-intercept form that passes through the following point with the given slope. Simplify your answer.
Point (5,−2); Slope=4/3
Answers
-2=(4/3)(5)+C
-2=(20/3) + C
C=-2-(20/3)
Find the LCM which is 3
C= -26/3
Therefore the equation is
Y=(4/3)x -26/3
Find the values of x and y in the equation below.

Answers
Answer:
The answer is a^6 b^18
Step-by-step explanation:
Triangle ABC has vertices A(1, 3), B(–2, –1) and C(3, –2). What are the coordinates of the triangle after the reflection over the line x = y?
Answers
Answer:
a(3,1)
b(-1,-2)
c(-2,3)
Step-by-step explanation:
6x + 45 is less than or equal to 240
Answers
Answer: neither
Step-by-step explanation:
To get rid of the fractions, we pick a useful number and multiply both sides of the equation by that number. The number is useful if multiplying eliminates all fractions.
2) Jamar buy a puppy from the Pet Store for $550 and the sales tax is 7%. What is the total price?
Answers
Answer:
Step-by-step explanation:
550.00x.07=38.50
550.00+38.50=588.50
To find ∫ (x − y) dx + (x + y) dy directly, we must parameterize C. Since C is a circle with radius 2 centered at the origin, then a parameterization is the following. (Use t as the independent variable.)
x = 2 cos(t)
y = 2 sin(t)
0 ≤ t ≤ 2π
With this parameterization, find the followings
dy=_____
dx=_____
Answers
Answer:
Step-by-step explanation:
Hello, please consider the following.
\(x=x(t)=2cos(t)\\\\dx=\dfrac{dx}{dt}dt=x'(t)dt=-2sin(t)dt\)
and
\(y=y(t)=2sin(t)\\\\dy=\dfrac{dy}{dt}dt=y'(t)dt=2cos(t)dt\)
Hope this helps.
Do not hesitate if you need further explanation.
Thank you
The values of dx and dy are give as -2sin(t)dt and 2cos(t)dt respectively. The answer to the given problem can be stated as,
dy = 2cos(t)dt
And, dx = -2sin(t)dt.
What is the integration of a function?The integration can be defined as the inverse operation of differentiation. If a function is the integration of some function f(x) , then differentiation of that function is f(x).
The given integral over C is ∫ (x − y) dx + (x + y) dy.
And, the parameters for C are as follows,
x = 2cos(t)
y = 2sin(t)
0 ≤ t ≤ 2π
Now, on the basis of these parameters dx and dy can be found as follows,
x = 2cos(t)
Differentiate both sides with respect to t as follows,
dx/dt = 2d(cos(t))/dt
=> dx/dt = -2sin(t)
=> dx = -2sin(t)dt
And, y = 2sin(t)
Differentiate both sides with respect to t as follows,
dy/dt = 2d(sin(t))/dt
=> dy/dt = 2cos(t)
=> dy = 2cos(t)dt
Hence, the value of dx and dy as per the given parameters is -2sin(t)dt and 2cos(t)dt respectively.
To know more about integration click on,
https://brainly.com/question/18125359
#SPJ2
How do you find the vertex angle of an isosceles triangle?
Answers
what is the sum 3/x+9+5/x-9
Answers
Answer:
\(\frac{8}{x}\)
Step-by-step explanation:
what is the sum 3/x+9+5/x-9
\(\frac{3}{x} + 9 + \frac{5}{x} - 9 =\) (add \(\frac{3}{x}\) and \(\frac{5}{x}\))
\(\frac{8}{x} + 9 - 9 =\) (solve 9 - 9 = 0)
\(\frac{8}{x}\) ( your answer)
Angle ADB and CD are straight lines. angle ADC = 5 x angle CDB Work out the size of angle ADC.

Answers
Answer:
Step-by-step explanation:

Simplify using the vertical method

Answers
This method can be used to quickly obtain the product of two polynomials.A-6k²+25k²-16k-15.
What is expression?Expression in math is a combination of numbers, symbols and operators that represent a mathematical quantity or operation. It can be a single number, a single variable, or a combination of numbers, variables and symbols combined together to form a mathematical statement. An expression can also include functions, such as polynomials, exponential functions, or logarithmic functions.
The vertical method involves writing the terms of the two factors side by side and multiplying them together to get the product.
(3k+5) (2k²-5k-3)
6k³ + 0k² + 0k + -15
0k³ + 10k² + -15k + 0
0k³ + 5k² + -15k + 0
0k³ + 0k² + 15k + 0
Adding the terms in each column yields the product:
A-6k³+25k²-16k-15
Therefore, the correct answer is A-6k³+25k²-16k-15.
In conclusion, using the vertical method can simplify algebraic multiplication problems by breaking them down into columns and adding the terms in each column. This method can be used to quickly obtain the product of two polynomials.
To know more about expression click-
brainly.com/question/1859113
#SPJ1