An electric utility worker wants to anchor a guy wire from the top of a 20.4 -foot utility pole to a spot that is 8.5 feet from the base of the pole on level ground. How long does the guy wire need to be? Round your answer to one decimal place.

Answers
Answer:
using Pythagorean theorem
c raised to the power of 2 is equals to 20.4 raised to the power of 2 + 72.25 raised to the power of 2
which is 416.16+72.25
which is 488.41
which is 488 appropriated to the nearest one decimal place
Related Questions
Please help thank you

Answers
Answer:
x = 140
Step-by-step explanation:
Using the exterior angle rule ( an exterior angle of a triangle is equal to the opposite interior angles of a triangle )
x is the interior angle and the given angles ( 50 and 90 ) are the opposite interior angles
So
x = 50 + 90
50 + 90 = 140
x = 140
Note: there is a right angle ( indicated by the little square. A right angle has a measure of 90 degrees so that's where the 90 came from)
Compute 90, 91, 92, 93, 94, and 95. 90 = 1 91 = 9 92 = 81 93 = 729 94 = 6561 95 = 59049 Make a conjecture about the units digit of 9n, where n is a positive integer. If n is even, the units digit of 9n is 1 . If n is odd, the units digit of 9n is 9 . Use strong mathematical induction to prove your conjecture. Submit your proof as a free response. (Submit a file with a maximum size of 1 MB.)
Answers
Answer:
Step-by-step explanation:
First we compute \(9^n\), for \(n = 0,1,2,3,4,5\)
\(9^0=1,9^1=9,9^2=81,9^3=729,9^4=6561,9^5=59049\)
We have the unit digit of \(9^n\), is either 1 or 9
Therefore, the conjecture can be state as follows
Conjecture; the unit of digit of \(9^n\), is 1, when n is even and 9 when n is odd
Let the property p(n) be the formula;
"The unit digit of \(9^n\), is 1 when n is even and 9 when n is odd"↔ P(n)
To show p(n) is true , we will use strong mathematical inductive
Show tgat p(0) and p(1) are true
We have to show the unit digit of \(9^0\) is 1 and \(9^1\) is 9
Since any integer with zero power is one and hence
\(9^0=1\) and \(9^1 = 9\)
Therefore, p(0) and p(1) are true
Show that for al integer \(k\geq 1\), if p(i) is true for all integer i from o through k, then p(k+1) is also true
let k be any integer with \(k \geq 1\) and suppose that for all integer i with \(0 \leq i \leq \leq k\)
the unit digit of \(9^i\) is 1 when is even and 9 when n is odd
we must show that \(9^{k +1}\) equals 1 when n is even and 9 when n is odd
Case I; (k +1 is odd)
in this case k is even and so, by inductive hypothesis, the unit digit of \(9^k\) is 1 and hence there is some non negative integer q such that
\(9^k = 10q + 1\)
now, \(9^{k+1}=9^k(9)\)
= (10q + 1)9
= 90q + 9
= 10.9q + 9
Note that for any non negative integer q , 9q is also an integer and this implies the unit digit of \(9^{k+1}\) is 9
Case II
(k +1 is even)
in this case k is odd and so, by inductive hypothesis, the unit digit of \(9^k\) is 9 and hence there is some non negative integer q such that
\(9^k=10q+9\)
Now,
\(9^{k+1}=9^k.9\\=(10q+9)9\\=90q+81\\=10(9q+8)+1\)
Note that any non negative integer q, 9q + 8 is also an integer and this implies the unit of \(9^{k+1}\) is 1
Since we have proved both the basis and the inductive step of the strong mathematical induction, we conclude that the given statement is true
Square root of 99 is between what two whole numbers
Answers
Answer:
The two whole numbers that are between the square root of 99 is, 9 and 10.
Step-by-step explanation:
Because 9 x 9 = 81 and 10 x 10 = 100
so 91 is between those two numbers.
and the square root of 81 is 9 and the square root of 100 is 10.
Is the number 90,040 divisible by 8?

Answers
Answer:
yes it is
Step-by-step explanation:
90,040/8 is 11222
What is the range of : 4,3,3,15,28
Answers
28-3
The range is 25
Find three consecutive integers who sum is 114?
Answers
Answer:
38
Step-by-step explanation:
38+38+38= 114
PLEASE HELP !! ILL GIVE BRAINLIEST *EXTRA POINTS*..
IM GIVING 40 POINTS !! DONT SKIP :((.

Answers
Answer: C
Step-by-step explanation: The layers of rocks implies superposition and changes in species implies evolution
One evening, Hazel and her brother each needed to use the family computer for part of their homework. They worked on their homework for 3 hours, and agreed to share the computer equally for that time.
How long did each person use the computer?
Write your answer as a proper fraction or mixed number.
Answers
Each person used the computer for \(\frac{3}{2}\) hours.
Define fraction.A fraction is a number that is a component of a whole. By breaking a whole into a number of parts, it is evaluated. For instance, the symbol for half of a complete number or item is 12. The components of a whole or group of items are represented by fractions. A fraction consists of two components. The numerator is the figure at the top of the line. It details the number of equal portions that were taken from the total or collection. The denominator is the figure that appears below the line. A fractional equation is one in which one or more of its terms have the unknown as their denominator.
Given Data
They worked on their homework for 3 hours, and agreed to share the computer equally for that time.
They share computer equally, so
\(\frac{time}{2}\)
Fraction - \(\frac{3}{2}\)
Each person used the computer for \(\frac{3}{2}\) hours.
To learn more about fractions, visit:
https://brainly.com/question/10354322
#SPJ13
what is the value of -2/3x0.6÷ 6/5
Answers
Answer:
-0.33333333333 in other word it o.3 with line over 3
Step-by-step explanation:
Describe the y-intercept and end behavior of the following graph:

Answers
Question 8 of 10
What is a point-slope equation of the line with slope -13 that goes through
the point (5, 7)?
A. Y-7 = -13(x - 5)
B. y + 5 = -13(x + 7)
0.000
C. y- 5 = -13(x-7)
D. y + 7 = -13(x + 5)
SUBMIT
Answers
Answer:
A
Step-by-step explanation:
The equation of a line in point- slope form is
y - b = m(x - a)
where m is the slope and (a, b ) a point on the line
Here m = - 13 and (a, b ) = (5, 7 ) , then
y - 7 = - 13(x - 5) → A
Help me ASPA PLEASE help

Answers
Answer:
85
Step-by-step explanation:
Question: 1/10 what is the equivalent percent and decimal?
Answers
Answer:
Decimal: 0.1
Percent: 10%
Step-by-step explanation:
Answer:
0.1 as decimal or 10% as percentage
How many thousands are in 680,000
Answers
Answer:
680
Step-by-step explanation:
The number of thousands in the number 680,000 will be 680.
What is Algebra?The analysis of mathematical representations is algebra, and the handling of those symbols is logic.
PEMDAS rule means for the Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This rule is used to solve the equation in a proper and correct manner.
The expanded form of a number is given by separating the number into its place.
The number is given below.
⇒ 680,000
Write the number 680,000 in the expanded form, then we have
680,000 = six hundred and eighty thousand
The number of thousands in the number 680,000 will be 680.
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ2
Prove that
(a) there exist integers m and n such that 2m + 7n = 1.
(b) there exist integers m and n such that 15m + 12n = 3.
(c) there do not exist integers m and n such that 2m + 4n = 7.
(d) there do not exist integers m and n such that 12m + 15n = 1.
(e) for every integer t, if there exist integers m and n such that 15m + 16n = t, then there exist integers rand s such that 3r + 8s = t.
(f) if there exist integers m and n such that 12m + 15n = 1, then m and n are both positive.
(g) for every odd integer m, if m has the form 4k + 1 for some integer k, then m + 2 has the form 4j - 1 for some integer j. (h) for every integer m, if m is odd, then m2 = 8k + 1 for some integer k.
(i) for all odd integers m and n, if mn = 4k - 1 for some integer k, then m or n is of the form 4} - 1 for some integer j.
Answers
LStep-by-step explanation:
(a) To proof this statement choose m = 4 and n = -1, from here we have 2(4) + 7(-1) = 1 as required. Hence th statement is true.
(b) To proof this statement choose m = 1 and n = -1, from here we have 15(1) + 12(-1) = 3 as required. Hence the statement is true.
(c) To proof this statement, suppose m and n are integers, since integers are closed under addition and multiplication then 2m, 4n and 2m + 4n are all integers. Obviously 2m and 4n are even integers, therefore their sum is also an even integer. This contradicts the equation 2m + 4m = 7, hence there do not exist integers m and n that satisfy the statement.
(d) To proof this statement, suppose m and n are integers, then 12m, 15n and 12m + 15n are all integers, since integers are closed under addition and multiplication. Factoring out 3 from the sum, we have: 3(4m + 5n). Therefore 3(4m + 5n) = 1 is a contradiction, because it will give 4m + 5n = 1/3 and addition of two integers can never give a fraction.
(e) To proof this statement, suppose m and n are integers, then 15m + 16n = t can be rewritten as 3(5m) + 8(2n) = t. Since integers are closed under multiplication, then 5m and 2n are integers. Let 5m = r and 2n = s, then we have: 3r + 8s = t as required.
(f) To proof this statement, suppose that m and n are both negative integers, we see that 12m + 15n = 1 is clearly impossible because the sum would be less than 0. Therefore, if there exist integers m and n such that 12m + 15n = 1, then they must be positive.
(g) To proof this statement, suppose m is an integer and has the form 4k + 1 for some integer k, then m + 2 = 4k + 1 + 2 = 4k + 3 = 4k + 4 - 1 = 4(k + 1) - 1. Since k is an integer then k + 1 is an integer because integers are closed under addition. Therefore, put j = k + 1. Hence we have 4j - 1.
(h) suppose that m is odd, then there is an n such that m = 2n + 1, therefore m² = (2n + 1)² = 4n² + 4n + 1 = 4(n² + n) + 1. Here, we need a lemma that says: suppose k is an integer, k(k + 1) is an even integer. This can be proven intuitively, when k is odd, the term in the bracket becomes even, and the whole expression is even. If k is even, then automatically the whole expression becomes even. Hence, our lemma is proven intuitively. This implies that n² + n is an even integer and can be replaced by 2k for some k that is an integer. Therefore, we have 4(2k) + 1 = 8k + 1 as required.
(i) suppose that m and n are odd integers such that mn = 4k - 1 for some k that is an integer. If we assume that neither m nor is in the for 4j - 1, then:
mn = (4a + 1)(4b + 1) for some a and b that are integers. Expanding that we have mn = 4(4ab + a + b) + 1 which is not in the form 4k - 1 for some k that is an integer as assumed. Therefore, if m and n are odd integers such that mn is in the form 4k - 1 for some k that is an integer, then m and n are in the form 4j - 1 for some j that is an integer.
Write a function rule for

Answers
Answer:
x^2
Step-by-step explanation:
1^2=1
2^2=4
3^2=9
What is the following product?
√12 √18
O√30
O 5√6
O 6√5
O 6√6
Answers
Answer: \(6\sqrt{6}\)
Step-by-step explanation:
\(\sqrt{12}=2\sqrt{3}\\\\\sqrt{18}=3\sqrt{2}\\\\\implies \sqrt{12} \sqrt{18}=2\sqrt{3}(3\sqrt{2}=\boxed{6\sqrt{6}}\)
The product of square root of 12 i.e.,√12 and square root of 18 i.e.,√18 is 6√6.
What is product law for exponent?When two numbers has equal power then we can multiply the the numbers and the power remains same. The number in the power is called exponent and the number is called as base. In \(a^m\), \(m\) is the exponent and \(a\) is the base of the number \(a^m\).
Step-by-step explanation:
\(\sqrt{12}\)\(=\sqrt{4}\)×\(\sqrt{3}\)\(=2\)×\(\sqrt{3}\) , since the square root of 4 is 2
\(\sqrt{18}=\sqrt{2}\)×\(\sqrt{9}\)\(=\sqrt{2}\)×\(3\) , since the square root of 9 is 3
Now, \(\sqrt{12} \sqrt{18} = 2\)×\(3\)×\(\sqrt{2}\)×\(\sqrt{3}\) from above.
\(=6\sqrt{6}\)
Hence the product of √12 and √18 is √12√18=6√6
To learn more about exponents click here:
https://brainly.com/question/27938922
#SPJ5
How do you factorise 6x-9
Answers
Answer:
6 x a number - 9 = factored
In this case, since the number is not declared as a specific number, this is the key to us factoring.
Like the number could be 6. ↓
Factoring:
\(6*6-9=27\\6*3-9=9\\6*9-9=45\)
bonus even factor:
\(6*2-9=3\)
These are factors and Least common multiples of 6 and 9.
Because 9 and 3 show up during half of the problem, and these are related to 6 and 9, the parents, we could measure this on a mathematical scale that this proves the factors correct.
There are other ways to factor this. See comments.
Question 9 (2 points)
Use this data set to answer the following question: 5, 10, 12, 4, 6, 11, 13,
5. Remember to show your work.
Calculate the mode.
Answers
Mode of the stated data set is 5.
What is defined as the mode of the data?The mode is the most frequently occurring value in a data set. A set of data can have one mode, multiple modes, or none at all.The mean, or average of a set, and the median, or middle value in a set, are two other popular central tendency measures.The mode in statistics is the most frequently occurring value in a set of data.The mode of the normal distribution has the same value also as mean and median.In many instances, the modal value would then differ from the data's average value.The given data set is;
5, 10, 12, 4, 6, 11, 13, 5.
Arrange the data in increasing order.
4, 5, 5, 6, 10, 11, 12, 13.
The maximum frequency is called mode.
thus,
mode = 5.
Therefore, mode of the given data set is 5.
To know more about the mode of the data, here
https://brainly.com/question/1529857
#SPJ9
Given f(x)=x^2+6x and g(x)=4 x^2, find fg. fg(x)=
Answers
The composite function f·g(x) is 4x⁴+24x³.
The given functions are f(x)=x²+6x and g(x)=4x².
We need to find f·g(x).
We know that, f·g(x)=f(x)×g(x)
Here, f·g(x)=(x²+6x)×4x²
= x²×4x²+6x×4x²
= 4x⁴+24x³
Therefore, the composite function f·g(x) is 4x⁴+24x³.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1
What is the approximate length of side GF in triangle EFG?

Answers
Answer:
41.93 degrees
Step-by-step explanation:

For each order pair, determine whether it is a solution to the system of equations.
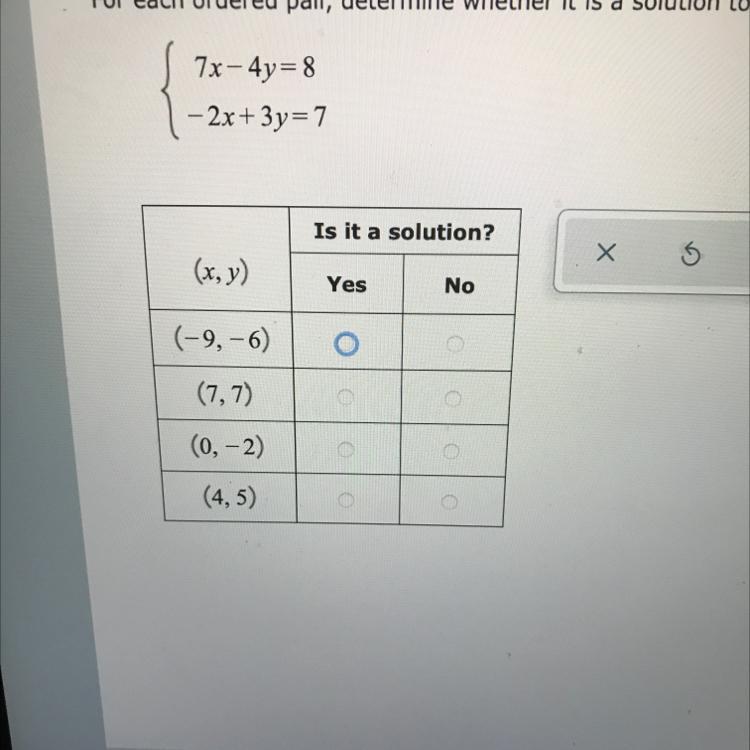
Answers
A ordered pair is a solution to the system if it satisfies all the equations of the system.
We have to check each equation for each pair.
We start with (-9,-6):
\(\begin{gathered} 7(-9)-4(-6)=8 \\ -63+24=8 \\ -39=8\longrightarrow\text{False} \end{gathered}\)As one of the equation is not satisfied, (-9,-6) is not a solution.
For (7,7) we have:
\(\begin{gathered} 7(7)-4(7)=8 \\ 49-28=8 \\ 21=8\longrightarrow\text{False} \end{gathered}\)As one of the equation is not satisfied, (7,7) is not a solution.
For (0,-2) we have:
\(\begin{gathered} 7(0)-4(-2)=8 \\ 0+8=8 \\ 8=8\longrightarrow\text{True} \end{gathered}\)As this equation is satisfied, we test the second equation:
\(\begin{gathered} -2(0)+3(-2)=7 \\ 0-6=7 \\ -6=7\longrightarrow\text{False} \end{gathered}\)As one of the equations is false, (0,-2) is not a solution.
Now, we test (4,5):
\(\begin{gathered} 7(4)-4(5)=8 \\ 28-20=8 \\ 8=8\longrightarrow\text{True} \end{gathered}\)As this equation is satisfied, we test the second equation:
\(\begin{gathered} -2(4)+3(5)=7 \\ -8+15=7 \\ 7=7 \end{gathered}\)The ordered pair (4,5) is a solution to the system.
Answer:
The only pair that is a solution is (4,5)
identify the nominal categorical variables in this study. (select all that apply.) A. voting yes percentage B. country C. issue type D. city E. year F. there are no nominal categorical variables.
Answers
Nominal categorical data is a categorical variable with two or more values, with no order. The examples of nominal categorical data here are the issue type, country, city.
Categorical data can be divided as two as per the variables. They are nominal and ordinal. In nominal categorical data, there will be two or more data points, but they are not ranked. The hair color can be red/blond/brown/black etc. But these cannot be ranked by taking one over the other.
In ordinal categorical data, there we can assign an order on the data points. Like grading system in marks of students, size comparison like large, medium, small. Here we could rank these in order.
Year can sometimes be nominal and sometimes ordinal. It is as per the context. If we are using it to calculate time it is ordinal.
So here we could not rank of variables in country, issue type, city. So all are nominal categorical data.
For more information regarding nominal and ordinal categorical data, kindly refer
https://brainly.com/question/30358526
#SPJ4
What is the value of x in the figure
shown?
37°
y
(3x + 1)
Answers
Answer:
x=4
Step-by-step explanation:
x=4 because when you have 3x+2=14 Subtract 2 from both sides. Then 3x+2−2=14−23x=12. Divide both sides by 3.3x3=123
The value of x in the figure having 3 angles on a line as shown in the image attached below is 28.
The angle is formed by two rays and a common point.
To calculate the value of x using the diagram attached below:
∠AOC+∠COD+∠BOD = 180° because the sum of all the angles on a line is 180°
On substituting the values from the figure,
∠AOC=3x-7
∠COD=55
∠BOD=x+20
∠AOC+∠COD+∠BOD =3x-7+55+x+20
3x-7+55+x+20=180
4x+68=180
4x=112
x=28
Thus, the value of x is 28 for the figure attached below.
Learn more about angles, here:
https://brainly.com/question/14569348
#SPJ6

Calculate the scale factor of LMN to OPQ. Enter answer as a whole
number or as a fraction in lowest terms, using the slash mark ( / ) for the
fraction bar.

Answers
Step-by-step explanation:
the scale factor is 1/1
both triangles are similar, and the scale factor is 1/1
Sukhir is 33 years old and earns $4,966 per month. He is married and has two children. They have a mortgage balance of $198,620 and other debt of $4,112. How much life insurance should he buy in order to provide his family with 10 years of income, pay off their debt, and pay for the children's education?
Answers
Sukhir should buy life insurance with a coverage amount of at least $898,652.
How much life insurance should Sukhir buy?To get amount of life insurance Sukhir should buy, we need to consider the followings:
10 years of income for his familyPaying off the mortgage balancePaying off other debtPaying for the children's educationSukhir's total income for 10 years is:
= 12 months x $4,966 x 10 years
= $595,920
We will add to amount needed to pay off the mortgage and other debt. The total amount needed is:
= $595,920 + $198,620 + $4,112
= $798,652
We will now add estimated cost of the children's education. Assuming each child will need $50,000 for their education. The total amount needed is:
= $798,652 + $50,000*2 child
= $798,652 + $100,000
= $898,652.
Read more about insurance premium
brainly.com/question/27870491
#SPJ1
what is −4/5+40/75+100%=
Answers
-0.8+1.875+100%
1.05+100%
0.1
Which decimal number represents two hundred twelve thousandths?
0.00212
0.212
200.12
212,000
Answers
Answer:
0.00212
Step-by-step explanation:
Option B, 0.212 represents two hundred twelve thousandths.
What are decimals?One of the number types in algebra that has a whole integer and a fractional portion separated by a decimal point is a decimal. The decimal point is the dot that appears between the parts of a whole number and a fraction.
Given a phrase two hundred twelve thousandths,
for the phrase tenth digit is 2,
the hundredth digit is 1 and the thousandth digit is 2
so the digit is 0.212
here 2 is in tenth place, 1 is at the hundredth place and 2 is on thousandth place,
Hence option B is correct.
Learn more about decimals;
https://brainly.com/question/29765582
#SPJ2
Boris started on the treadmill after setting timer for 99 minutes. The display says he have finished 43% of his run. How many minutes have gone by. Round to the nearest tenth
Answers
99 minutes * 0.43 = 42.57 minutes
Rounding to the nearest tenth, we can say that approximately 42.6 minutes have gone by.
What is the surface area and volume of the triangular prism?The triangular prism is 1 foot high. The triangle that forms the base of the prism has a base of 6 inches and a height of 4 inches. The two remaining sides of the triangular bases are each 5 inches long. What is the surface area and volume of the triangular prism?
Answers
Answer:
The surface area of the triangular prism is approximately 16.222 square feet, and the volume of the triangular prism is 12 cubic feet.
Step-by-step explanation:
formulas:
Surface Area = 2B + Ph
Volume = Bh
where B is the area of the triangular base, P is the perimeter of the base, h is the height of the prism, and B and h are both in the same units (inches, feet, etc.).
Given:
Height of the triangular prism = 1 foot
Base of the triangular prism = 6 inches
Height of the triangular base = 4 inches
Length of the other two sides of the triangular base = 5 inches
First, we need to find the area of the triangular base (B):
B = (1/2) x base x height
B = (1/2) x 6 inches x 4 inches
B = 12 square inches
Next, we need to find the perimeter of the triangular base (P):
P = sum of all three sides
P = 6 inches + 5 inches + 5 inches
P = 16 inches
Now, we can use the formulas to find the surface area and volume:
Surface Area = 2B + Ph
Surface Area = 2(12 square inches) + (16 inches)(1 foot)
Surface Area = 24 square inches + 16 square feet
Surface Area = 16.222 square feet (rounded to three decimal places)
Volume = Bh
Volume = 12 square inches x 1 foot
Volume = 12 cubic feet
Therefore, the surface area of the triangular prism is approximately 16.222 square feet, and the volume of the triangular prism is 12 cubic feet.