Amiyah keeps 120 beads in a storage box. She chooses a bead without looking, notes what color it is, and returns it to the box. She does this several times.
The table shows the results. Amiyah's niece wants to get her hair done with yellow beads. Based on the table, predict the number of yellow beads in Amiyah's storage box.
blue beads - 12
yellow beads - 7
white beads - 11

Answer: tan A=4/3

Step-by-step explanation:

Theo đề ta có: 5sinA=4 suy ra: sinA=4/5, mà ta đã biết là: sinA= cạnh đối/cạnh huyền, suy ra: cạnh đối của góc A =4, cạnh huyền =5

Áp dụng định lí py ta go ta đc:

5^2=4^2+x^2

=) x=3

Vậy cạnh kề của góc A=3

Mà tanA = cạnh đối/cạnh kề

Vậy giá trị của tanA=4/3

(bạn vẽ hình ra thì có thể nhìn rõ hơn đấy, cảm ơn bạn đã tham khảo câu trả lời của mik)

The length of the rectangle is approximately 41.34 inches.

Let's assume the width of the rectangle is represented by the variable w. According to the given information, the length of the rectangle is four less than twice the width, which can be expressed as 2w - 4.

The perimeter of a rectangle is calculated by adding the lengths of all four sides. In this case, the perimeter is given as 128 inches. Since a rectangle has two pairs of equal sides, we can set up the equation:

2w + 2(2w - 4) = 128.

Simplifying the equation, we get:

2w + 4w - 8 = 128,

6w - 8 = 128,

6w = 136,

w = 22.67.

So, the width of the rectangle is approximately 22.67 inches. To find the length, we can substitute this value back into the expression 2w - 4:

2(22.67) - 4 = 41.34.

Therefore, the length of the rectangle is approximately 41.34 inches.

In summary, the length of the rectangle is approximately 41.34 inches. This is determined by setting up a system of equations based on the given information: the perimeter of the rectangle being 128 inches and the length being four less than twice the width.

By solving the system of equations, we find that the width is approximately 22.67 inches, and substituting this value back, we obtain the length of approximately 41.34 inches.

To know more about length refer here:

https://brainly.com/question/2497593

#SPJ11

Answer:

\(f(x) = 15x^2 -14x - 8\)

\(g(x) = 5x + 2\)

Step-by-step explanation:

Represent the two polynomials with f(x) and g(x)

The question requires that we assume values for f(x) and g(x) as long as the condition in the question is met;

Let

\(f(x) = 15x^2 -14x - 8\)

\(g(x) = 5x + 2\)

To determine if the condition is met, we need to divide f(x) by g(x)

\(\frac{f(x)}{g(x)} = \frac{15x^2 -14x - 8}{5x + 2}\)

Factorize the numerator

\(\frac{f(x)}{g(x)} = \frac{15x^2 - 20x + 6x - 8}{5x + 2}\)

\(\frac{f(x)}{g(x)} = \frac{(5x + 2)(3x - 4)}{5x + 2}\)

Cross out 5x + 2

\(\frac{f(x)}{g(x)} = 3x - 4\)

The result is referred to as quotient, Q

\(Q = 3x - 4\)

Note that Q and g(x) have the same degree of 1

T A can be seen as a linear transformation from R^2 to R^3.

To find the range and codomain of the matrix transformation T A, we need to first determine the matrix T A . The matrix T A is obtained by multiplying the input vector x by A:

T A (x) = A x

Therefore, T A can be seen as a linear transformation from R^2 to R^3.

To determine the range of T A , we need to find all possible outputs of T A (x) for all possible inputs x. Since T A is a linear transformation, its range is simply the span of the columns of A. Therefore, we can find the range by computing the reduced row echelon form of A and finding the pivot columns:

A =  (\left[\begin{array}{cc}1 & 2 \ 1 & -2 \ 0 & 1\end{array}\right]) ~ (\left[\begin{array}{cc}1 & 0 \ 0 & 1 \ 0 & 0\end{array}\right])

The pivot columns are the first two columns of the identity matrix, so the range of T A is spanned by the first two columns of A. Therefore, the range of T A is the plane in R^3 spanned by the vectors [1, 1, 0] and [2, -2, 1].

To find the codomain of T A , we need to determine the dimension of the space that T A maps to. Since T A is a linear transformation from R^2 to R^3, its codomain is R^3.

If the functions were not linear, it would not make sense to talk about their range or codomain in this way. The concepts of range and codomain are meaningful only for linear transformations.

Learn more about  linear  from

https://brainly.com/question/2030026

#SPJ11

Answer: D

Step-by-step explanation: The expression can't be factored since there is no such thing as sum of squares. When two squares are being added, you usually can't factor them.

For 2, the answer is D

For 3, the answer is B

For 4, the answer is D

For 5, the answer is B

Answer:

1st option

Step-by-step explanation:

Given f(x) then f(x) + c is a vertical translation of f(x)

• If c > 0 then a shift up of c units

• If c < 0 then a shift down of c units

Here g(x) = \(\sqrt{x}\) - 19

The base graph f(x) has been shifted down 19 units

Hello! :)

\(\large\boxed{x = 14, 26}\)

Let one number be equal to x.

Since the other is 12 more, we can express this as x + 12.

Write an expression showing the sum of these two numbers equal to 40:

x + (x + 12) = 40

Combine like terms:

2x + 12 = 40

Subtract 12 from both sides:

2x = 28

Divide both sides by 2:

x = 14

This is the value of one of the numbers. Since the other number is "x + 12", we can solve for this value:

14 + 12 = 26.

The two numbers are 14 and 26.

\(=\sqrt{2} *\sqrt{2} *\sqrt{2} *\sqrt{2} \\=(\sqrt{2} *\sqrt{2})(\sqrt{2} *\sqrt{2})\\=2*2\\=4\)

The answer is 4

The value of \((\sqrt2)^4\) is 4.

The number of times a number has been multiplied by itself is referred to as its exponent. The rules of multiplying exponents are of different types. The given equation can be calculated using the Power of a Power rule.

According to this rule, when a base has an exponent, and that entire term has an exponent, the exponents are multiplied together. This is written as

\((a^x)^y=a^{xy}\)

Here, both exponents are multiplied together.

Therefore, using the above rule the given square root with an exponent can be written as,

\(\begin{aligned}\left(\sqrt2\right)^4&=\left(2^{\frac{1}{2}\right)^4\\&=2^{\frac{1}{2}\times4}\\&=2^2\\&=4\end{aligned}\)

The value is 4.

To know more about the exponent rule:

https://brainly.com/question/24420843

Answer:

(-13, -3)

Step-by-step explanation:

Elimination is used to get either the y or the x to cancel out in both equations. In this case, you'd have to multiply the first equation by -3, so it would be 9x + 21y = -54. Now that you did that, you can "subtract" the two equations. 9x - 9x = 0 (they cancel each other out). 21y - 2y = 19y. -54 - 3 = -57. Now that we're left with 19y = -57, let's find out what y is by solving out the equation. The answer would be y = -3. Now that we have this info, we can substitute the y in one of the two equations to find the x. I'm going to use the first equation. -3x - 7(-3) = 18 --> -3x + 21 = 18 --> -3x = 39. The result is x = -13. Therefore, the answer is (-13, -3).

Answer:

\(\huge\boxed{Q = 110 \textdegree, \ ST = 9 \ \text{ft}}\)

Step-by-step explanation:

When we reflect and transform a figure, the angle lengths nor the side lengths are touched. The side length only changes if we dilate or stretch the figure, and the angle length only changes if we stretch the figure.

Therefore, we know the information is going to be the exact same. We just have to figure out what corresponds to what from JKLM to QTSR.

If we reflect a figure across a horizontal reflection line through its center, the figure will just flip sides. M will be J, L will be K, etc.

When we translate this down, nothing changes except its position. So we can pretend these two shapes are right on top of each other for now.

When we move these right on top of each other, we can see that Angle J overlaps with Angle Q. Since they don't have any weird intersects, we know that angle J will be equal to Angle Q. Since we already know J is 110°, we know Q is also 110°.

When we move it on top, we also see that KL overlaps with ST perfectly. Since we know KL is 9, that must mean ST is also 9.

Hope this helped!

The slope of a line perpendicular to the line is -4

The equation is x -4y = 28

The equation for the line is

y = mx + c

where m = slope

c = y-intercept

Here the equation is x - 4y = 28

4y = x - 28

y = x/4 - 7

So the slope of this line is 1/4

Now we have to find the slope of the line perpendicular to that line.

We know that,

m1 × m2 = -1

1/4 × m2 = -1

m2 = -4

Therefore the slope of the line perpendicular to the line is -4.

To know more about the slope of the line refer to the link given below:

https://brainly.com/question/22057368

#SPJ1

The complete question is:

Find the slope of a line perpendicular to x-4y=28

Answer:

➡Heigth = 4.77in

Step-by-step explanation:

➡Volume = \(\pi × r^2\) × H

➡\(60 = 3.14 × 2^2 × H\)

➡\(60 = 3.14 × 4 × H\)

➡\(H = \frac{60}{3.14 × 4} \approx \bf 4.77in\)

I hope this helps!

Answer:

-20

Step-by-step explanation:

48 divided by -3 is -16 but you round up since its high enough and it goes to -20

Answer:

Hi... Do this for prove that

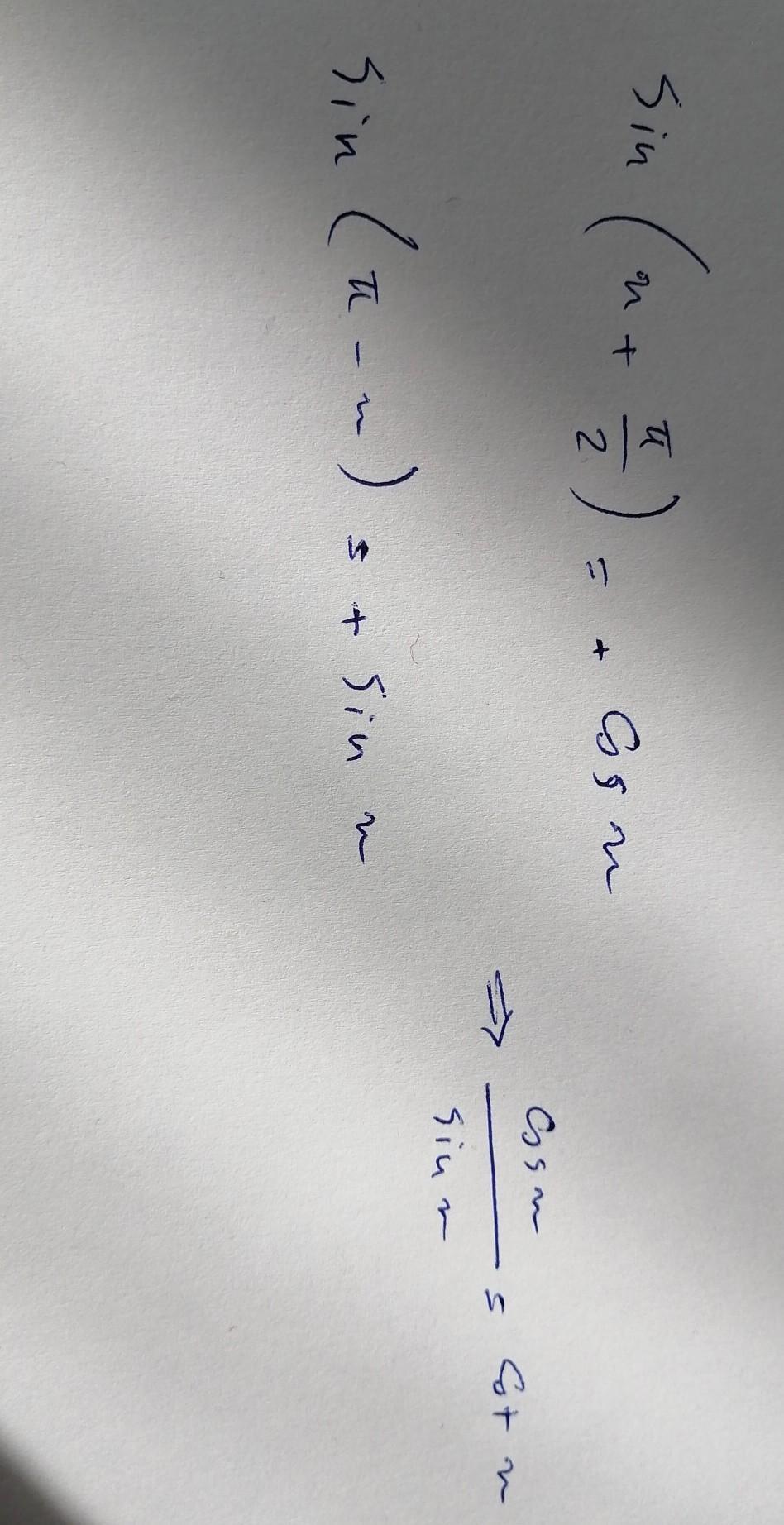
Answer:

Step-by-step explanation:

Answer:

Its 0

Step-by-step explanation:

Hope this helps!

Answer:

i don't no that's why i download this

Answer:

Step-by- explanation:

4x(3y+1) and if u need it simplified x(12y+4)

Step-by-step explanation:

integral from 0 to 2pi of cos3x

(sin3x)/3 from 0 to 2 pi

sin 6pi /3 - sin 0 /3 = 0

D) A^2 = A + 1 this equation represents diagonal matrices with the same eigenvalues on the diagonal.

Let λ be an eigenvalue of the matrix A, and let v be the corresponding eigenvector. Since A is diagonalizable, we can write A = PDP^(-1), where D is the diagonal matrix containing the eigenvalues on the diagonal, and P is the matrix whose columns are the eigenvectors.

We know that A^2 = A + 1, so we can substitute A with its diagonalizable form:

(PDP^(-1))^2 = PDP^(-1) + 1.

Expanding the square and applying the matrix multiplication rules, we get:

PD^2P^(-1) = PDP^(-1) + 1.

Since D is a diagonal matrix, D^2 will have the eigenvalues squared on the diagonal. Therefore, we have:

P(D^2)P^(-1) = PDP^(-1) + 1.

Multiplying both sides by P^(-1) on the right, and by P on the left, we obtain:

D^2 = D + 1.

This equation holds because P^(-1)P = I (the identity matrix), and D and D^2 are diagonal matrices with the same eigenvalues on the diagonal.

Therefore, the correct answer is D) A^2 = A + 1.

Learn more about eigenvalues

Answer:

D. x > -3 and x < 1

Step-by-step explanation:

There is an absolute value in this inequality, so we have to solve for 2 instances -- where the quantity in the absolute value is positive, and where it is negative.

First, we will isolate the absolute value by dividing by 3:

3|x + 1| < 6

|x + 1| < 2

Then, because this is a less-than case of the absolute value, we can put it in between the positive and negative absolute values of the other side:

-|2| < x + 1 < |2|

-2 < x + 1 < 2

and solve.

-3 < x < 1

(this can also be written as x > -3 and x < 1)

Answer:

28 degrees

Step-by-step explanation:

68 = 2m + 12

56 = 2m

m = 28 degrees

Answer:

You are going to spend $3.48 in total.

Step-by-step explanation:

You need to add the two numbers together.

1.49+1.99=$3.48

You are going to spend $3.48 in total. (I'm assuming we aren't supposed to include tax)

Answer:

I know this problem is an  

✔ equation

because it has an equals sign.

The t is the  

✔ variable

.

The negative sign is the  

✔ operation

.

The 7 and the 8 are both  

✔ constants

.

Step-by-step explanation: i took the test :( crying cuz im bouta fail

Answer:

B

Step-by-step explanation:

\(Tan \ A = \dfrac{Opposit \ side \ A}{Adjacent \ side \ of \ A}\\\\Tan \ A = \dfrac{16}{12}=\dfrac{4}{3}\)

Answer:

(a+4)(a-7)

Step-by-step explanation:

Bring 3a to the left and equate it to zero. Using the product sum method find 2 numbers, which give the product when multiplied and give the sum when added. Use them to factor out

Answer:

(a + 4)(a - 7)

Step-by-step explanation:

a^2 - 3a - 28

Factors of 28: 1, 2, 4, 7, 14, 28

4 - 7 = -3

(a + 4)(a - 7)

now to check:

(a • a) + (a • -7) + (4 • a) + (4 • -7)

(a^2) + (-7a) + (4a) + (-28)

a^2 - 7a + 4a - 28

a^2 - 3a - 28

Answer:

624.102

Step-by-step explanation:

pls give brainliest im new and need points

1. In the context of spacetime, the locus of points equidistant from the origin of a spacetime plane is a hyperbola.

In Euclidean space, the distance between two points is given by the Pythagorean theorem, which only considers spatial dimensions. However, in spacetime, the concept of distance is extended to include both spatial and temporal components. The spacetime distance, also known as the interval, is given by the Minkowski metric:

ds^2 = -c^2*dt^2 + dx^2 + dy^2 + dz^2,

where c is the speed of light, dt represents the temporal component, and dx, dy, dz represent the spatial components.

To determine the locus of points equidistant from the origin, we need to find the set of points where the spacetime interval from the origin is constant. Setting ds^2 equal to a constant value, say k^2, we have:

-c^2*dt^2 + dx^2 + dy^2 + dz^2 = k^2.

If we focus on a spacetime plane where dy = dz = 0, the equation simplifies to:

-c^2*dt^2 + dx^2 = k^2.

This equation represents a hyperbola in the spacetime plane. It differs from a circle in Euclidean space due to the presence of the negative sign in front of the temporal component, which introduces a difference in the geometry.

Therefore, the locus of points equidistant from the origin in a spacetime plane is a hyperbola.

(Note: The explanation provided assumes a flat spacetime geometry described by the Minkowski metric. In the case of a curved spacetime, such as that described by general relativity, the shape of the locus of equidistant points would be more complex and depend on the specific curvature of spacetime.)

To know more about equidistant, refer here:

https://brainly.com/question/29886221#

#SPJ11

Answer:

I have no idea

Step-by-step explanation:

Answer:

Hey there!

p(x)=7x+25

7x+25=60

7x=35

x=5

Let me know if this helps :)