Alex is 6 years older than Frank. The sum of their ages is 50. Find Alex's age and
Frank's age.
HELP
Answers
Answer: Alex 28
Frank 22
Step-by-step explanation: Age difference is 6. Addition is 50
Related Questions
For the last several weeks, Carol has been saving the coins from her waitressing tips so that she can buy her grandmother a music box for her birthday. If there are 70% more quarters than dimes in the money Carol has saved, and the combined value of her quarters and dimes is $31.50, how many dimes does she have
Answers
To check our answer, we can verify that the number of quarters is 1.7 times the number of dimes, which would be 102. And the total value of her dimes and quarters would be: $31.50
What is Algebraic expression ?
Algebraic expression can be defined as combination of variables and constants.
Let's start by using algebra to solve the problem.
Let x be the number of dimes that Carol has saved.
According to the problem, there are 70% more quarters than dimes. We can express the number of quarters in terms of x as 1.7x, since 1.7 times the number of dimes is equal to the number of quarters.
We also know that the combined value of her quarters and dimes is $31.50. We can express this as an equation:
0.10x + 0.25(1.7x) = 31.50
Simplifying and solving for x, we get:
0.10x + 0.425x = 31.50
0.525x = 31.50
x = 60
Therefore, Carol has 60 dimes.
Therefore, To check our answer, we can verify that the number of quarters is 1.7 times the number of dimes, which would be 102. And the total value of her dimes and quarters would be:
60 * $0.10 (dimes) + 102 * $0.25 (quarters) = $31.50
which matches the information given in the problem.
To learn more about Algebraic expression from given link.
brainly.com/question/953809
#SPJ1
An experiment is completed where a coin is flipped and a six-sided die (singular for dice) is rolled. The outcomes from the experiment are shown, where H represents heads and T represents tails. H1, H2, H3, H5, H6, T1, T1, T2, T3, T5. What percent of the outcomes included tails with an off number greater than 1? 1.) 16 2/3% 2.) 25% 3.) 33 1/3% 4.) 41 2/3%
Answers
Answer:
1) \(16\frac{2}{3}\)% or 20%
Step-by-step explanation:
Given that:
An experiment which is carried out by flipping a coin and rolling six sided die.
The outcomes can be:
{H1, H2, H3, H5, H6, T1, T1, T2, T3, T5}
As per question statement:
Number of outcomes having tails and an odd number greater than one is 2 (i.e. T3 and T5)
Total number of outcomes here is 10.
Therefore, to find the percentage, we use the following formula:
\(\dfrac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}}\times 100\)
\(\Rightarrow \dfrac{2}{10}\times 100 = 20\%\)
As per question statement, the answer is 20%.
If we consider all the outcomes, i.e.
{H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}
Total number of outcomes = 12
The percentage will come out be :
\(\Rightarrow \dfrac{2}{12}\times 100 = 16\frac{2}{3}\%\)
a carnival has a game where players can win stuffed animals. the rules allow for players to win no more than 10 small animals, no more than 6 large animals, and no more than 12 total animals. let x
Answers
The form of a system of inequalities that would allow you to solve for the number of each type of animal that can be won is 10x + 6y = 12.
Given:
A carnival has a game where players can win stuffed animals. the rules allow for players to win no more than 10 small animals, no more than 6 large animals, and no more than 12 total animals.
x be the number of small animals and y be the number of large animals
The number of small animals = 10x
Number of large animals = 6y
The equation:
= 10x + 6y = 12.
Therefore the form of a system of inequalities that would allow you to solve for the number of each type of animal that can be won is 10x + 6y = 12.
Learn more about the inequalities here:
https://brainly.com/question/28823603
#SPJ4
24.7% of the products in the local shop are specialty soaps. 76% of those soaps are made with fresh herbs. if there are 350 bars of specialty soap in the shop, approximately how many of them are not made with fresh herbs? round your answer up to nearest whole number
Answers
we know that 76% of the specialty soaps are made with fresh herbs, and we also know that there are a total of 350 specialty soap bars, so how many are made with fresh herbs? well, just 76% of those 350
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{76\% of 350}}{\left( \cfrac{76}{100} \right)350}\implies 266\)
Which of the following is a univariate display of quantitative data? histogram mosaic plot bar chart scatterplot
Answers
A histogram is a univariate display of quantitative data that organizes data into bins and shows the frequency of observations within each bin.
A histogram is a graphical representation that displays the distribution of quantitative data. It consists of a series of contiguous bars, where each bar represents a specific range or bin of values, and the height of the bar corresponds to the frequency or count of observations falling within that range.
Histograms are commonly used to visualize the shape, central tendency, and spread of a dataset. By examining the heights of the bars, one can determine the frequency of values within each bin and identify patterns such as peaks or clusters. This makes histograms an effective tool for exploring the distribution and characteristics of a single variable in a dataset.
Learn more about Dataset here: brainly.com/question/24058780
#SPJ11
Consider the equation 1.5 x plus 4.5 y equals 18.
If we graph the equation, what is the slope of the graph?
Answers
can someone help please

Answers
Answer:
39.3078
Step-by-step explanation:
i am not for sure but i belive this is correct:)
2. A swimming pool has a volume of 32,700
cubic feet. How many gallons of water does
the pool hold?
A. 4,371.66 gal
B. 239,360 gal
C. 244,596 gal
D. 4,278.07 gal
Answers
Answer:
C. 244,596 gal
Step-by-step explanation:
To determine the number of gallons of water that a swimming pool holds, you can use the following formula:
gallons = cubic feet * 7.48
Plugging in the given volume of 32,700 cubic feet, you get:
gallons = 32,700 cubic feet * 7.48
= 244,596 gal
Therefore, the swimming pool holds approximately 244,596 gallons of water.
The polynomial equation x^3−x^2+kx−3=0
has three roots that are all integers.
Find the value of integer k
Answers
The value of integer k is -5.
What is polynomial equations ?
Polynomial equations formed with variables, exponents and coefficients .
Since the polynomial has three integer roots, we can express it as:
(x - r1)(x - r2)(x - r3) = 0
where r1, r2, and r3 are the three integer roots.
Expanding the left-hand side, we get:
x^3 - (r1 + r2 + r3)x^2 + (r1r2 + r1r3 + r2r3)x - r1r2r3 = 0
Comparing this with the given polynomial, we see that:
r1 + r2 + r3 = 1
r1r2 + r1r3 + r2r3 = k
r1r2r3 = 3
First we need to find the value of k. From the first equation, we see that one of the roots must be 1, since the sum of three integers that are not 1 cannot be 1. Without loss of generality, assume that r1 = 1. Then we have:
r2 + r3 = 0
r2r3 = 3
Since the roots are integers, the only possibility is r2 = -3 and r3 = 1.
Therefore, we have:
k = r1r2 + r1r3 + r2r3 = 1(-3) + 1(1) + (-3)(1) = -5
Therefore, the value of integer k is -5.
Learn more about polynomial equation here :brainly.com/question/28947270
#SPJ1
Find the average value of the function f(x)=rseer on the interval 3.14/4 . A chain that weighs 0.55 pounds per foot is used to lift a 70 pound bucket of water up a well that is 60 feet deep. Luckily, you checked the bucket for holes before filling it, and there are no leaks. Find the work done to lift the bucket out of the well.
Answers
The work done to lift the bucket out of the well is:
Work = 103 pounds × 60 feet = 6180 foot-pounds.
To find the average value of the function f(x) = √x on the interval [3.14/4], we need to evaluate the definite integral of the function over that interval and divide it by the length of the interval.
The average value of f(x) on the interval [a, b] is given by:
Avg = (1/(b - a)) * ∫[a to b] f(x) dx
In this case, the interval is [3.14/4]. Evaluating the integral, we have:
Avg = (1/(3.14/4 - 3.14/4)) * ∫[(3.14/4) to (3.14/4)] √x dx
= (1/(0)) * 0
= undefined
Since the length of the interval is zero, the average value of the function on this interval is undefined.
Regarding the work done to lift the 70 pound bucket of water up a 60-foot deep well using a chain that weighs 0.55 pounds per foot, we can calculate it using the formula:
Work = Force × Distance
The force required to lift the bucket is the weight of the bucket plus the weight of the chain. The weight of the bucket is 70 pounds, and the weight of the chain is given by:
Weight of chain = (0.55 pounds/foot) × (60 feet) = 33 pounds
Therefore, the total force is 70 pounds + 33 pounds = 103 pounds.
The distance over which the force is applied is the depth of the well, which is 60 feet.
Hence, the work done to lift the bucket out of the well is:
Work = 103 pounds × 60 feet = 6180 foot-pounds.
learn more about "Work ":- https://brainly.com/question/25573309
#SPJ11
The graph of f(x) is shown below of g(x) and f(x) are inverse functions, which graph represents g(x)

Answers
Answer:
It's B
Step-by-step explanation:
Given that we have the graph of f(x), we want to see which one is the graph of its inverse. i just had that question and i got a 100 on it
Mrs. Bergstedt teaches four classes. Each class has 15 students. Her first class has 9 juniors, her second class has 12 juniors, her third class has 6 juniors, and her fourth class has 3 juniors. If Mrs. Bergstedt chooses four students at random, what is the probability that exactly two of the students are juniors (rounded to the nearest thousandth)?
Answers
The probability that exactly two of the students are juniors is given as follows:
0.270 = 27%.
What is the hypergeometric distribution formula?The mass probability formula is presented as follows:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}C_{N-k,n-x}}{C_{N,n}}\)
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
The parameters are:
x is the number of successes.N is the size of the population.n is the size of the sample.k is the total number of desired outcomes.The values of these parameters for this problem are given as follows:
\(N = 60, n = 4, k = 18\)
Hence the probability that exactly two of the students are juniors is calculated as follows:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}C_{N-k,n-x}}{C_{N,n}}\)
\(P(X = 2) = h(2,60,4,18) = \frac{C_{18,2}C_{42,2}}{C_{60,4}} = 0.270\)
More can be learned about the hypergeometric distribution at https://brainly.com/question/14741653
#SPJ1
?
m∠ABD = m∠ABC
AB ≅ BC
B is the midpoint of DC.
m∠DBC = 90°
Answers
Answer:
50*
Step-by-step explanation:
Q1) (15 pts) a) Find the complementary (homogeneous) solution of y(5) — y(3) = f(t). b) Determine the particular solution yp (t) if (i) f(t) = et (ii) f(t) = 2t² (iii) f(t) = (3t+2) Cos2t Using the method of undetermined coefficients (Do not calculate the coefficients). (Other methods will not be graded.) 2) (10 pts) Find a linear differential equation whose general solutions is y(x) = C₁e* + C₂xe* + C3e *Cos 2x + C4e-*Sin 2x
Answers
1a) Complementary solution: y(t) = c₁ + c₂e^t + c₃e^(-t) + c₄cos(t) + c₅sin(t)
1b) Particular solutions:
(i) yp(t) = (1/2)e^t
(ii) yp(t) = (1/5)t^2 + (2/15)
(iii) yp(t) = [(3/20)t^2 + (1/4)t + C₁]cos(2t) - [(3/40)t^3 + (1/8)t^2 + C₂]sin(2t)
2) Linear differential equation: y''(x) + 4y'(x) + 5y(x) = 0
1a) To find the complementary solution of y(5) - y(3) = f(t), we need to find the homogeneous solution of the differential equation y(5) - y(3) = 0. We assume that y(t) = e^(rt) and substitute it into the differential equation to obtain the characteristic equation:
r^5 - r^3 = 0
r = 0, ±1
Since there are three distinct roots, the complementary solution is of the form:
y(t) = c₁ + c₂e^t + c₃e^(-t) + c₄cos(t) + c₅sin(t)
where c₁, c₂, c₃, c₄, and c₅ are constants.
1b) Using the method of undetermined coefficients, we can determine the particular solution of y(5) - y(3) = f(t) for each of the given functions f(t):
(i) f(t) = e^t
Assuming yp(t) = Ae^t, we obtain:
A(e^(5t) - e^(3t)) = e^t
A = 1/2
yp(t) = (1/2)e^t
(ii) f(t) = 2t^2
2A(t^5 - t^3) + 6B(t^3 - t) + 6C(t^2 - 1) = 2t^2
A = 1/5, B = 0, C = 2/15
yp(t) = (1/5)t^2 + (2/15)
(iii) f(t) = (3t+2)cos(2t)
A''(t)cos(2t) + B''(t)sin(2t) + 4A'(t)sin(2t) - 4B'(t)cos(2t) = (3t+2)cos(2t)
A(t) = (3/20)t^2 + (1/4)t + C₁
B(t) = -(3/40)t^3 + (1/8)t^2 + C₂
yp(t) = [(3/20)t^2 + (1/4)t + C₁]cos(2t) - [(3/40)t^3 + (1/8)t^2 + C₂]sin(2t)
2) The given general solution is:
y(x) = C₁e^x + C₂xe^x + C₃e^(-x)cos(2x) + C₄e^(-x)sin(2x)
y'(x) = C₁e^x + C₂(e^x + xe^x) - C₃e^(-x)sin(2x) + C₄e^(-x)cos(2x)
y''(x) = C₁e^x + C₂(2e^x + xe^x) + C₃e^(-x)cos(2x) - C₄e^(-x)sin(2x)
(C₁ + C₂ + C₃ + C₄)e^x + (2C₂ + C₂x - C₃sin(2x) + C₄cos(2x))e^x + (-C₁ + 2C₂ - C₃cos(2x) - C₄sin(2x))e^(-x) = 0
Since this equation must hold for all values of x, we obtain the following system of equations:
C₁ + C₂ + C₃ + C₄ = 0
2C₂ - C₁ - C₃cos(2x) - C₄sin(2x) = 0
C₂x - C
To know more about linear differential equation, visit:
brainly.com/question/30323408
#SPJ11
A certain colony of bacteria began with one cell and the population doubled ever20 minutes what was the population of the colony after 2 hours
Answers
Tthe population of the colony after 2 hours is 64a
What was the population of the colony after 2 hoursFrom the question, we have the following parameters that can be used in our computation:
Rate = doubles every 20 minutes
Represent the initial population with a
So, we have the following representation
f(t) = a(2)^t
Where t is the number of 20 minutes in the time
The time is given as 2 hours
So, we have
t = 2 hours/20 minutes
Evaluate
t = 6
The function becomes
f(t) = a(2)^6
Evaluate
f(t) = 64a
hence, the population is 64a
Read more about function at
https://brainly.com/question/15316908
#SPJ1
please help i will give brainliest, thanks

Answers
Answer:
2x-2 -2 is the y intercept and the 2x is the rate of change its easy lol
Step-by-step explanation:
Answer:
a
Step-by-step explanation:
Forty percent of a number is greater than one-half the number decreased by 15. Which inequality can be used to determine the number?A 40x > x /2 - 15B 40x > 2x - 15C 0.40x > x/2 - 15D 0.4x < x/2 - 15
Answers
The inequality can be used to determine the number is 0.4x > x/2 - 15
The term inequality means the unequal relationship between the two or more expressions.
Here we have given that Forty percent of a number is greater than one-half the number decreased by 15.
And we need to find the number that is used to determine the inequality.
While we looking into the given question, let us consider x be that unknown number.
Then based on the given statement, we have divide it into two parts.
First, forty percent of the number and it can be written as 40%x or 0.4x.
Next is one-half the number is 1/2 x or x/2
When we combine the whole statement,
Then we get the inequality,
=> 0.4x > x/2 - 15
Therefore option (c) is correct.
To know more about inequality here.
https://brainly.com/question/28823603
#SPJ4
28. Sum of three numbers in an AP is 21 and their product is 231. Find the numbers.
Answers
Step-by-step explanation:
let the three numbers be
(a-d) ,(a) and (a+d)
so we have the sum as
a-d+a+a+d=21
3a=21
a=7..............(1)
we have d product as
(a-d)(a)(a+d)=231
(a²-d²)(a)=231
a³-ad²=231..........(2)
subtitue (1) in (2)
we have
(7)³-(7)d²=231
343-7d²=231
343-231=7d²
112=7d²
d²=112/7
d²=16
d=±4
when d=-4
the first number is
a-d=7-(-4)=7+4=11
second number is
a=7
third number
a+d=7+(-4)=7-4=3
when d=4
the first number is
a-d=7-4=3
the second number is
a=7
the third number is
a+d=7+4=11
For each integral, indicate what trig function would be used to solve using trigonometric substitution. (No work to show.) a) ∫ x 2 +4 x 2 dx b) ∫ 16−9x 2 x 2 dx c) ∫ 5x 2 −3 x 2 dx
Answers
As per the trigonometric substitution the value of the integrals are
a) ∫ x² + 4 / x² dx is 2 tan θ
b) ∫ (16 - 9x²) / x² dx is (4/3) sec θ
c) ∫ (5x² - 3) / x² dx is (1/√3)tanθ
Let's take a look at the given integrals:
a) ∫ x² + 4 / x² dx
For this integral, we can use the trigonometric substitution x = 2tanθ. This substitution simplifies the integral and allows us to solve it using trigonometric identities.
b) ∫ (16 - 9x²) / x² dx
To solve this integral, we can use the trigonometric substitution x = (4/3)secθ. This substitution simplifies the expression under the integral sign and allows us to use trigonometric identities to solve the integral.
c) ∫ (5x² - 3) / x² dx
For this integral, we can use the trigonometric substitution x = (1/√3)tanθ. This substitution simplifies the integral and allows us to use trigonometric identities to solve it.
To know more about integral here
https://brainly.com/question/18125359
#SPJ4
I NEED HELP PLEASE!! WILL GIVE CROWN!!
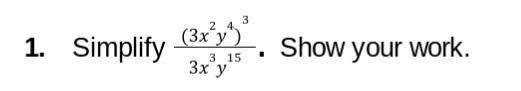
Answers
Answer:
9x^3/y^3
Step-by-step explanation:
Hope this helps!
20 pts help meee!!!!

Answers
Answer:
measure the area inside of the shapes, and multiply it. online answers better than me sorry.
Step-by-step explanation:
Answer: Ask teacher
Step-by-step explanation:
Solve for k. NO LINKS OR FILES WILL GIVE BRAINLEST!!!

Answers
k=16*11
k= 176
HELPP MEeee PLEASE I'll give u kizz

Answers
Answer:
Don't want any but here's your answer
Step-by-step explanation:
He spends $165 on 20 gallons
Find the percent of decrease. Round to the nearest whole percent. 428 to 377
Answers
Answer:14
Step-by-step explanation:
Mr. Johnson gives five tests during the marking period. If Ralph needs a 65 average to pass this marking period and his first four grades are 60, 72, 55, and 80, then what is the lowest score he
can earn on the last test to have a passing
average?
A. 58
B. 65
C. 76
D. 80
Answers
Answer:
58
Step-by-step explanation:
60+72+55+80=267
267+58=325
325/5=65
Four friends are in a marathon. After 3 hours, each friend has completed a different portion of the race.
Name
Alejandro
Beth
Christina
DeAngelo
Portion of Race
Completed
65%
3
5
0. 7
18
25
Which friend has completed the greatest portion of the race?
Answers
Alejandro has completed the greatest portion of the race (65%).
The friend who has completed the greatest portion of the race is Alejandro, with 65% of the race completed. This is because 65% is greater than the other portions completed by the other friends: 3/5 (or 60%), 0.7 (or 70%), and 18/25 (or 72%). Therefore, Alejandro has completed the greatest portion of the race.
A portion of a race can refer to different distances depending on the race. For example, a marathon race is typically 26.2 miles long and can be divided into several different portions, such as the first 5 miles, the middle 8 miles, and the last 13.1 miles. In a shorter race such as a 5K or 10K, the portions may be shorter and more specific, such as the first quarter-mile or the second lap of the course.
Portions of a race are often used as checkpoints to help runners stay on pace and measure their progress during the race.
Learn more about a portion of the race:
https://brainly.com/question/1096276
#SPJ11
help?? please i need it

Answers
Answer:
I think the answer is no because none of these are divisible by any of the numbers
determine whether there are any transient terms in the general solution cos(x) dy dx (sin(x))y = 1
Answers
The general solution of the given differential equation is
cos(x) y = [y ln|sec(x) + tan(x)| - C] x.
Therefore, we do not have any transient terms in the general solution
cos(x) dy dx (sin(x))y = 1.
Note: A transient solution is a solution of a differential equation that goes to zero as time goes to infinity.
The given differential equation is
cos(x) dy dx (sin(x))y = 1.
Here, the independent variable is x, and the dependent variable is y.To determine whether there are any transient terms in the general solution
cos(x) dy dx (sin(x))y = 1,
we need to find its general solution as follows:Integrating the given differential equation, we have:
∫(sin(x))y dy = ∫sec(x) dx
On integrating the above expression, we get:
(cos(x)/y) + C = ln|sec(x) + tan(x)|
Here, C is the constant of integration.
Now, we can express the general solution of the given differential equation as follows:
cos(x) y = [y ln|sec(x) + tan(x)| - C] x
(multiplying both sides by x)
Therefore, the general solution of the given differential equation is
cos(x) y = [y ln|sec(x) + tan(x)| - C] x.
Therefore, we do not have any transient terms in the general solution
cos(x) dy dx (sin(x))y = 1.
Note: A transient solution is a solution of a differential equation that goes to zero as time goes to infinity.
To know more about transient terms visit:
https://brainly.com/question/30666770
#SPJ11
A soup can in the shape of a cylinder is 4 inches tall and has a radius of 2 inches. How much soup will fit in the can? Use 3. 14 for Pi and round the answer to the nearest tenth. Recall the formula V = pi r squared h. 12. 6 16. 0 25. 1 50. 2.
Answers
Answer:
V = 50.3 in ^2
Step-by-step explanation:
The volume of a cylinder is given by
V = pi r^2 h
We know the radius is 2 and the height is 4
V = (3.14) * (2)^2 * 4
V =50.24
Rounding to the nearest tenth
V = 50.3 in ^2
Help ASAP!! Geometry -
Find the volume of the solid. (FSSS!) Round answers to the nearest hundredth.

Answers
Answer:
x = 9.27 cm
Volume = 289.2 cm³
Step-by-step explanation:
SA = Surface Area
SA = 229.2 cm²
P = Perimeter of Base
P = 3(6)
P = 18 cm
H = Height of Solid
H = x
A = Area of Base(Equilateral Triangle)
A = 6²√3 / 4
A = 36√3 / 4
A = 9√3
A = 9(1.732)
A = 31.176
A = 31.2 cm²
SA = Surface Area
SA = PH + 2A
229.2 = 18x + 2(31.2)
229.2 = 18x + 62.4
229.2 - 62.4 = 18x
166.8 = 18x
9.266 = x
9.27 = x
x = 9.27 cm
V = Volume
V = AH
V = 31.2(9.27)
V = 289.224
V = 289.2 cm³